Universal order-parameter and quantum phase transition for two-dimensional q-state quantum Potts model

Yan-Wei Dai(代艳伟)， Sheng-Hao Li(李生好)， and Xi-Hao Chen(陈西浩)

1Centre for Modern Physics and Department of Physics，Chongqing University，Chongqing 400044，China

2Chongqing Vocational Institute of Engineering，Chongqing 402260，China

3Research Institute for New Materials and Technology，Chongqing University of Arts and Sciences，Chongqing 400000，China

Keywords: quantum phase transitions，universal order parameter，fidelity

1. Introduction

Quantum phase transitions (QPTs)[1]occur at absolute zero temperature due to the Heisenberg uncertainty relation and are driven by quantum fluctuations. The core of the QPT consists of the Hamiltonian and its energy spectrum， which have been well studied through the development of various numerical methods. In particular，tensor network algorithm[2–12]is a very powerful tool to study the strongly correlated quantum lattice systems. To date， most QPTs can be described based on the spontaneous-symmetry-breaking order of the Landau–Ginzburg–Wilson paradigm. However， this local order parameter is model dependent and hard to be defined. In addition，not all phases can be described by symmetry-broken order， such phases correspond to QPTs beyond the Landau–Ginzburg–Wilson paradigm.[13–16]

Recently， for one-dimensional systems of infinite size，Liuet al.[17]presented a universal order-parameter concept based on the fidelity between a ground state and its symmetrytransformed counterpart. The advantage of the universal order parameter over local order parameters is the former’s universality in characterizing QPTs in quantum lattice many-body systems， in the sense that the universal order parameter is not model dependent，in contrast with model-dependent order parameters. Reference [18] extends the universal order parameter from one-dimensional systems of infinite size to onedimensional finite-size systems. Herein we further extend the use of the universal order parameter to two-dimensional quantum systems. To test the pertinence of the universal order parameter to describe two-dimension lattice symmetry， we also calculate the ground-state fidelity per lattice site and quantum coherence.

Quantum fidelity is a basic notion in quantum information science and is an approach to study QPTs in strongly correlated many-body systems.[19–28]As a measure of distance between two quantum states，quantum fidelity provides a measure of the similarity between two quantum states. When a system undergoes a QPT， the ground-state fidelity dramatically changes upon passing through the critical point in phase space， with the “pinch point” being the signature of the phase transition. In addition， the quantification of quantum coherence[29]has also revealed intriguing connections between correlation and quantum coherence.[30–32]A variety of quantum coherence measures have been introduced to detect QPTs， such as the quantum Jensen–Shannon divergence，[33]the relative entropy of coherence，[29]and thel1norm of coherence.[29]

The present work investigates 2-， 3-， and 4-state quantum Potts models on a square lattice and the quantum Ising model on a honeycomb lattice by using the infinite projected entangled-pair state algorithm[3，4，7]in two dimensions. Here，we employ a simplified scheme to update the ground-state wave function. The infinite time-evolving block decimation(iTEBD) method[2]will be used to calculate iPEPS groundstate wave function withχbeing the bond dimension. In order to calculate the observable physical quantity， the corner transfer matrix renormalization method[34]is implemented to contracted vironmental tensor withMbeing the environment dimension. The remainder of this paper is organized as follows. In Section 2，the two-dimensionalq-state quantum Potts mode is introduced. Section 3 discusses the universal order parameter for 2-， 3-， and 4-state quantum Potts models on a square lattice and the quantum Ising model on a honeycomb lattice， and explains how the universal order parameter provides a model-independent way to characterize QPTs in manybody systems.Section 4 discusses the ground-state fidelity per lattice site，and Section 5 shows how quantum coherence measures can serve to detect QPTs. Finally，a summary is given in Section 6.

2. The q-state quantum Potts model in two dimensions

We now consider theq-state quantum Potts model[27，35]in a transverse magnetic field in two dimensions. Theqstate is described by the Hamiltonian

3. Universal order parameter

Reference [17] explains the concept of a universal order parameter. For any translation-invariant quantum lattice system of the symmetry groupG， if the system undergoes a QPT with symmetry order， the universal order parameter can be used to characterize the QPT. The ground-state fidelityF(ψ，gψ)between a ground state|ψ〉and its symmetrytransformed counterpartg|ψ〉， whereg ∈Gis any symmetry operation， can be written asF(ψ，gψ)=|〈ψ|g|ψ〉|. The ground-state fidelity asymptotically scales as [fg(λ)]L，[20–26]withLbeing the system size. As detailed in Refs.[17，18，28]，the universal order is

Given a control parameterλin the symmetry phase， thenIg(λ)=0. For a control parameterλin the symmetry-broken phase，the universal order parameterIg(λ)ranges from zero to unity. Note thatIg(λ)satisfies features of the order parameter.In fact， to characterize a quantum lattice many-body system with global symmetry groupGspontaneously broken，the universal order parameter is model independent.

Fig. 1. The universal order parameter I(λ) for (a) the quantum Ising model， (b) the quantum three-state Potts model， and (c) the quantum four-state Potts model in a transverse magnetic field λ on the square lattice for different bond dimension χ.

Figures 1(a)–1(c) show the universal order parameterI(λ)as a function of transverse magnetic fieldλfor the quantum Ising model，the three-state quantum Potts model，and the four-state quantum Potts model，respectively，with a transverse magnetic field imposed on a square lattice and for various bond dimensionsχ. The results show that the universal order parameterI(λ) is nonzero in theZqsymmetry-broken phase but zero in the symmetry phase. The variations in the universal order parameterI(λ) indicate that the many-body system undergoes a QPT when the control parameterλcrosses the phase-transition point. The pseudo critical points are as follows:

(a)λc=3.273，3.222，3.213 and 3.212 with the bond dimensionχ= 2，4，6，8 and the environment dimensionM=12，16，20，22 for the quantum Ising model， respectively. Indeed， the pseudo critical points obtained by using the simplified updating scheme for the quantum transverse Ising model on the square lattice compares rather poorly with the resultλc= 3.044330(6) from the most accurate quantum Monte Carlo;[43]

(b)λc=2.62，2.616 and 2.616 with the bond dimensionχ= 3，6，9 and the environment dimensionM= 16，20，22 for the three-state quantum Potts model， respectively. The estimateλc= 2.616 is consistent with the known estimateλc～2.58;[44]

(c)λc=2.43，2.428 and 2.428 with the bond dimensionχ=4，6，8 and the environment dimensionM=16，20，22 for the four-state quantum Potts model，respectively.

These results are consistent with those of Ref.[27].

Figure 2 plots the universal order parameterI(λ) as a function ofλfor the quantum Ising model on a honeycomb lattice. The pseudo critical pointλcoccurs atλc=2.216，2.206 and 2.20 for the bond dimensionsχ=4，6，9 and the environment dimensionM=16， 20， 22， respectively. The quantum Ising model on a honeycomb lattice has been much less studied. A high-precision Monte Carlo estimate gives a critical point ofλc=2.13250(4).[45]

These results indicate that pseudo critical points in twodimensional systems can be located by using the universal order parameterI(λ). In addition，the universal order parameterI(λ)is continuous for the Ising model，while the universal order parameterI(λ)is abrupt forq=3 andq=4. The continuous(discontinuous)behavior of the universal order parameterI(λ)indicates that Ising model on the square(honeycomb)lattice undergoes a continuous phase transition andq=3 andq=4 state Potts undergo a discontinuous phase transition on the square lattice.

Fig.2. The universal order parameter I(λ)as a function of λ for quantum Ising model on the honeycomb lattice.

4. Ground-state fidelity per lattice site

Fidelity is a measure of the“similarity” of two quantum states. The ground-state fidelityF(λ1，λ2)=|〈ψ(λ2)|ψ(λ1)〉|asymptotically scales asF(λ1，λ2)～d(λ1，λ2)Lwithλ1andλ2being two values of the control parameterλ，whereL=Lx×Lyis the size of the two-dimensional lattice for the two given ground states|ψ(λ1)〉and|ψ(λ2)〉. Here，d(λ1，λ2) is the ground-state fidelity per lattice site， characterizing how fast the fidelity tends to zero in the thermodynamic limit，[20–26]defined as

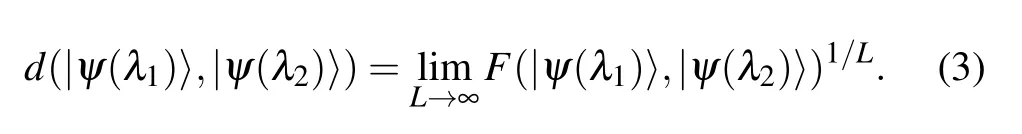
The ground-state fidelity per lattice site，d(λ1，λ2)， satisfies the inherited properties of (i) range [0≤d(λ1，λ2)≤1]， (ii)normalization[d(λ，λ)=1]， and(iii)symmetry[d(λ1，λ2)=d(λ2，λ1)]. With the tensor network representation， the ground-state fidelity per lattice site，d(λ1，λ2)， is the largest eigenvalue of the transfer matrix.[26]

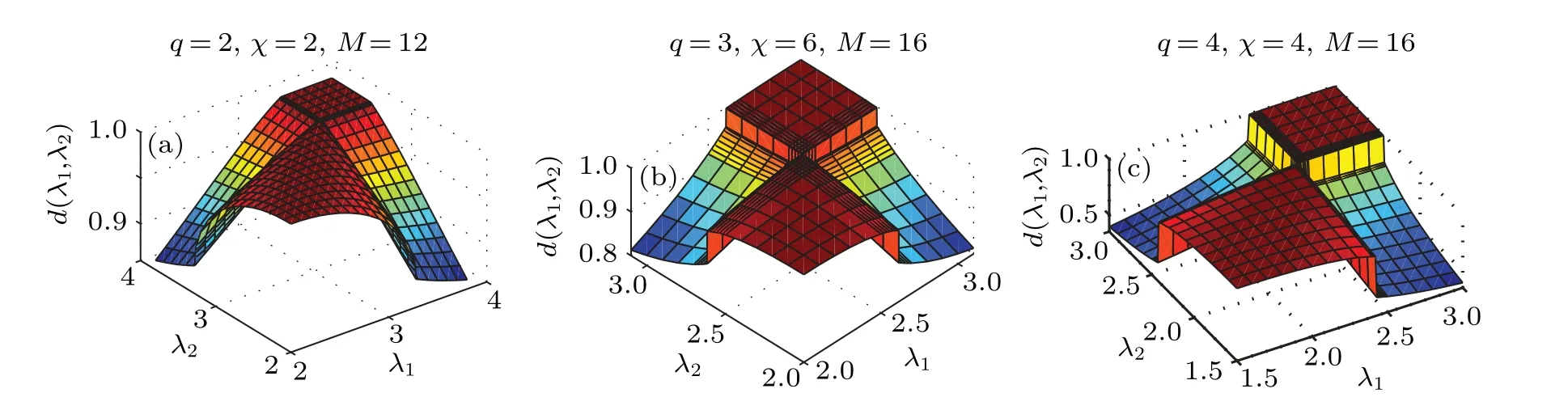
Fig.3. The ground state fidelity surface defined by the ground state fidelity per site， d(λ1，λ2)， as a function of the transverse magnetic field λ1 and λ2 for(a)the quantum Ising model，(b)the quantum three-state Potts model，and(c)the quantum four-state Potts model on the square lattice. The pseudo critical point λc occurs as a pinch point on the ground state fidelity surface.

Figures 3(a)–3(c)plot the ground-state fidelity per lattice site，d(λ1，λ2)，as a function of the control parametersλ1andλ2for the quantum Ising model，the three-state quantum Potts model， and the four-state quantum Potts model， respectively，with a transverse magnetic field applied to the square lattice.A pinch point corresponding to the QPT point appears on the ground-state fidelity surface. The pinch point is located atλc=3.273 for the quantum Ising model with the bond dimensionχ=2 and the environment dimensionM=12[Fig.3(a)]，λc=2.616 for the three-state quantum Potts model with the bond dimensionχ=6 and the environment dimensionM=16[Fig. 3(b)]， andλc= 2.43 for the four-state quantum Potts model with the bond dimensionχ=4 and the environment dimensionM=16[Fig.3(c)].

Figure 4 plots the ground-state fidelity per lattice site，d(λ1，λ2)， as a function of the control parametersλ1andλ2for the quantum Ising model on a honeycomb lattice. With the square lattice， a pinch point appears on the ground-state fidelity surface. Note that the pinch point is at the intersection of two singular lines that characterize the phase-transition points. The pseudo critical point is located atλc=2.216 for the quantum Ising model with the bond dimensionχ=4 and the environment dimensionM=16 on the honeycomb lattice.Thus，the phase-transition pointsλcobtained from the fidelity per lattice site are consistent with the results from the universal order parameter. In addition，the results constitute another example of the connection between(i)pseudo critical points for a quantum many-body system undergoing a QPT[19–21]and(ii) pinch points on a fidelity surface. The fidelity per lattice site can distinguish continuous(discontinuous)quantum phase transition according to the continuous(discontinuous)behavior of fidelity near the critical point. From the surface of the fidelity per lattice site，we can also see thatq ≥3 Potts model undergoes a discontinuous phase transition on the square lattice. Ising model undergoes a continuous phase transition on the square lattice and honeycomb lattice，respectively.

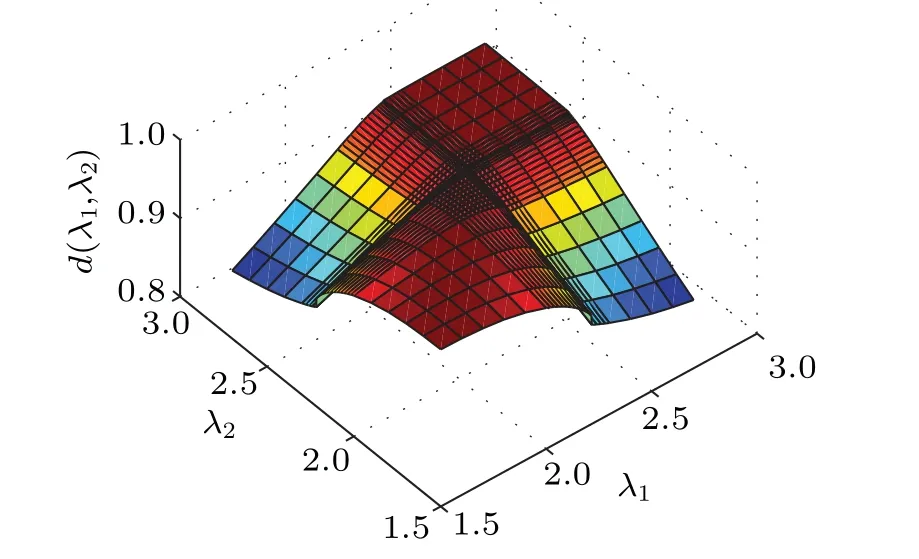
Fig.4. The ground state fidelity surface defined by the ground state fidelity per site，d(λ1，λ2)，as a function of the transverse magnetic field λ1 and λ2 for the quantum Ising model on the honeycomb lattice.

5. Quantum coherence measures

This section discusses the connection between various quantum coherence measures and a quantum many-body system undergoing a QPT. We consider three coherence measures: the quantum Jensen–Shannon divergence， the relative entropy of coherence，and thel1norm of coherence.The quantum Jensen–Shannon divergence[33]is

whereρis the density matrix，andρdiagcontains the diagonal elements of the density matrixρ.

The relative entropy of coherence[29]is

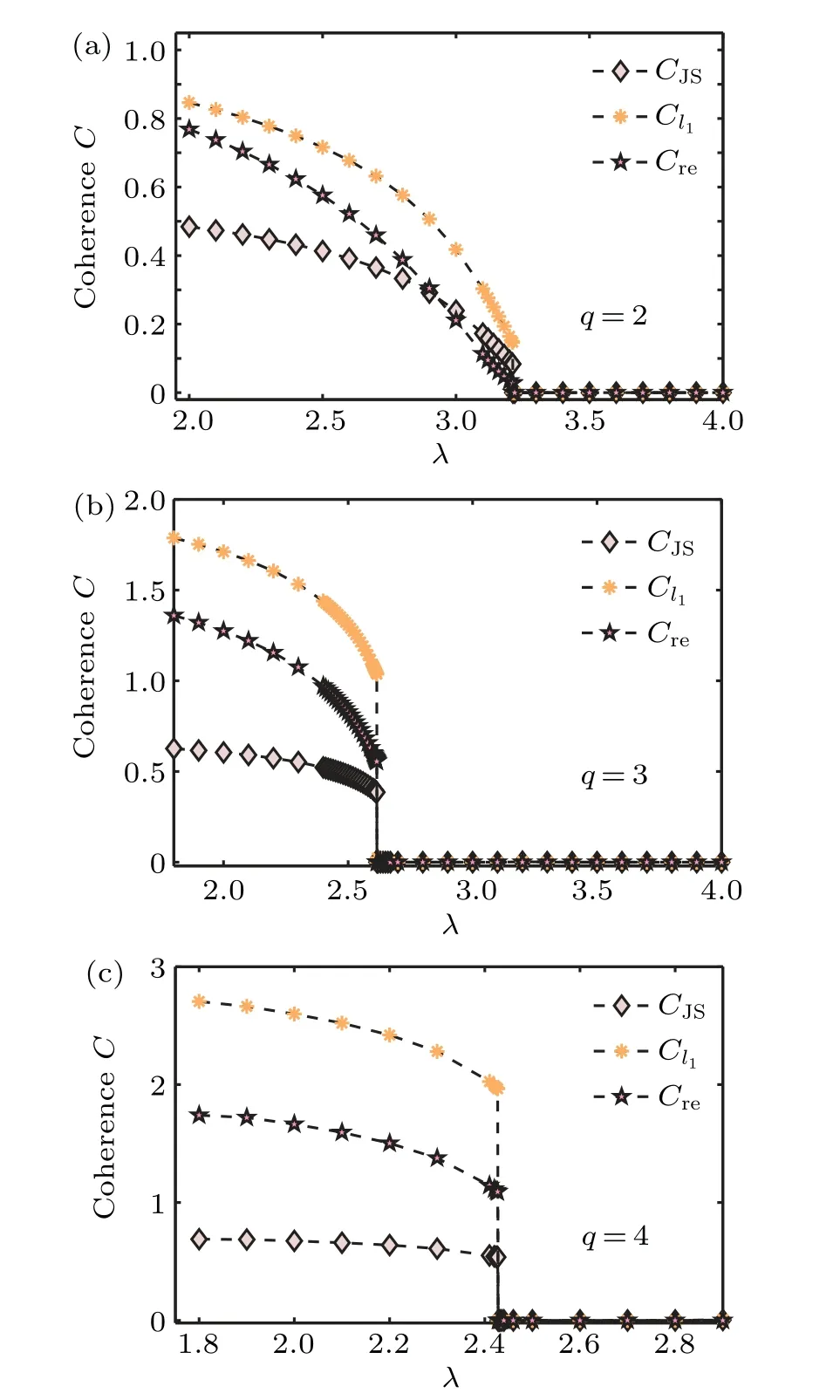
Fig. 5. Quantum coherence measures C as a function of the transverse magnetic field λ for (a) the quantum Ising model with χ = 6 and M =20， (b) the quantum three-state Potts model with χ =9 and M =22， and (c) the quantum four-state Potts model with χ =8 and M=22 on the square lattice.

Thel1norm of coherence[29]is

whereρnmdenotes the off-diagonal elements of the density matrixρ. Finally，Sis the entanglement entropy and is defined asS=-Trρlog2ρ.

Figures 5(a)–5(c) plot the three coherence measures as a function ofλfor the quantum Ising model， the three-state quantum Potts model，and the four-state quantum Potts model，respectively， on a square lattice. The pseudo critical point is located atλc=3.213 withχ=6 andM=20 [Fig. 5(a)]，λc=2.616 withχ=9 andM=22[Fig.5(b)]，andλc=2.428 withχ=8 andM=22 [Fig. 5(c)]. The result is consistent with the results for the universal order parameter and for the ground-state fidelity per lattice site. Figure 6 also plots the three coherence measures as a function ofλfor the quantum Ising model on a honeycomb lattice. The pseudo critical point is atλc=2.20 with the bond dimensionχ=9 and the environment dimensionM=22， which is consistent with the results from the universal order parameter and the ground-state fidelity per lattice site. These results show that quantum coherence measure detects the QPT in a two-dimensional lattice system. In addition， quantum coherence can also distinguish continuous and discontinuous phase transitions.

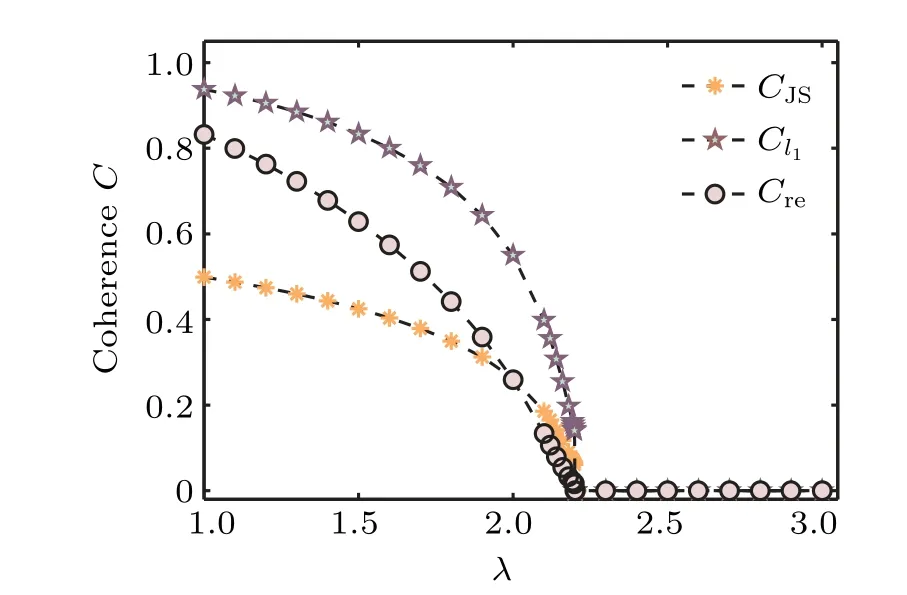
Fig.6. Three quantum coherence measures C as a function of the transverse magnetic field λ for the quantum Ising model on the honeycomb lattice，with χ =9 and M=22.

6. Summary

We investigate herein the QPTs for 2-， 3-， and 4-state quantum Potts models on a square lattice and for the Ising model on a honeycomb lattice by using the infinite projected entangled-pair state algorithm with the simplified updating scheme. We extend the universal order parameter to a twodimensional system. The universal order parameter， groundstate fidelity per lattice site， and a variety of quantum coherence measures are used to characterize QPTs. The universal order parameter can be used to explore QPTs with symmetrybroken order for any translation-invariant quantum lattice system of the symmetry groupG. Although the universal order parameter is zero in a symmetric phase， it ranges from zero to unity in symmetry-broken phase. When the control parameter crosses the critical point， the universal order parameter changes， which implies that the system undergoes a QPT at the phase-transition point.We also discuss the groundstate fidelity per lattice site and identify the pinch point near the critical point on the fidelity surface， which corresponds to the QPT point. Finally， we discuss three quantum coherence measures: the quantum Jensen–Shannon divergence，the relative entropy of coherence， and thel1norm of coherence.These measures have singularities at the critical point， which identifies the QPTs. By using the universal order parameter，the ground-state fidelity per lattice site and the quantum coherence measures provide consistent positions for the phasetransition point. From the universal order parameter， the surface of the fidelity per lattice site and the quantum coherence measures，Our results show that Ising model undergoes a continuous phase transition on the square lattice and honeycomb lattice，respectively. And 3，4-state Potts model undergo a discontinuous phase transition on the square lattice. We expect the universal order parameter，ground-state fidelity per lattice site， and quantum coherence measures to provide further insights into critical phenomena in strongly correlated manybody quantum lattice systems of any dimensionality.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 11805285)， Natural Science Foundation of Chongqing of China (Grant No. cstc2020jcyjmsxmX0034)，and the Science and Technology Research Program of Chongqing Municipal Education Commission(Grant No.KJQN 201900703).