Gap solitons of spin–orbit-coupled Bose–Einstein condensates in PT periodic potential
S Wang(王双), Y H Liu(刘元慧), and T F Xu(徐天赋),†
1Hebei Key Laboratory of Microstructural Material Physics,School of Science,Yanshan University,Qinhuangdao 066004,China
2School of Science,Yanshan University,Qinhuangdao 066004,China
Keywords: gap solitons,spin–orbit coupling,PT-symmetric periodic potential
1. Introduction
Spin–orbit coupling (SOC) is a fundamental effect in quantum mechanics and plays an indispensable role in condensed matter physics.[1–3]However, because of the difficulty of adjusting the coupling in practical materials, there are certain limitations to the adjustable region of SOC strength. As Rashba and Dresselhaus have achieved SOC experimentally,[4]more and more works are enthusiastic about studying SOC effects in BECs system. The new door to the ultra-cold atom quantum system is thus opened, which creates many new possibilities for observing and analyzing quantum phenomena at the macro level. The SOCBECs effect also shows many interesting localization phenomena, such as solitons,[5–9]band gap solitons[10–12]and vortex structures.[13,14]
The concept of thePTperiodic potential firstly appeared in the study of quantum operators and their spectra.[15,16]In 1998,Bender and Boettcher proposed the idea that some non-Hermitian Hamiltonian can have a real spectrum in the specific parameter domain.[17]Even if the Hamiltonian has a non-Hermitian property, it has a complex potential that follows thePTperiodic potential. The specified potential satisfiesU(x)=U*(-x),thus Hamiltonian can also have a completely real eigen spectrum.[18]The operatorPis the parity reflection operator,representing the space inversion transformation of the quantum state, andTis the time inversion operator.The effects of the two operators on the coordinate operatorxand the momentum operatorpare defined asP:x →-x,p →-p,T:i→-i,t →-t,andp →-p.[19]ThePTperiodic potential requires that the complex potential must satisfy the real part as an even function and the imaginary part an odd function. The most interesting feature of this Hamiltonian is the existence of a critical threshold. Beyond this threshold,thePTsymmetry will be broken and the system will undergo a sudden phase transition.[20,21]The pioneering work of Bender and Boettcher has broadened the way for the development of symmetric quantum mechanics. The unique property ofPTsymmetry has been introduced into many important fields of physics.[22–27]It has already been realized in optical systems[28,29]and developed into BECs system in recent years.[30–32]
In this article, we carefully analyze the properties of the gap solitons in the SOC-BECs system with thePTperiodic potential. We have discovered a new type of gap solitons in the SOC-BECs system in thePTperiodic potential by the Newton method. The single-peak and double-peak band gap solitons in the first band gap are investigated for their space distribution and stability. We have also researched the influence of the depths and periods of the imaginary part ofPTperiodic potential on these gap solitons. We prove that the band gap solitons in the SOC-BECs system with thePTperiodic potential exist steadily in the corresponding band gap.The depth of the imaginary part of thePTperiodic potential affects the stability of the gap solitons in the first band gap,but the period does not produce important influence.
This article is organized as follows. In Section 2,we use the dimensionless coupled Gross–Pitaevskii equation to illustrate the system. In Section 3, we get the linear Bloch spectrum and Bloch waves by solving the equations,and determine the position of the linear band gap. In Section 4,we show the characteristics of the gap solitons with different depths and periods of the imaginary part of thePT-symmetric potential. In Section 5, we discuss the influence of the depths and periods of the imaginary part on the stability of the gap solitons. Section 6 is a summary.
2. Theoretical model
Our mean-field model of the SOC-BECs system is given by the one-dimensional coupled Gross–Pitaevskii(GP)equation

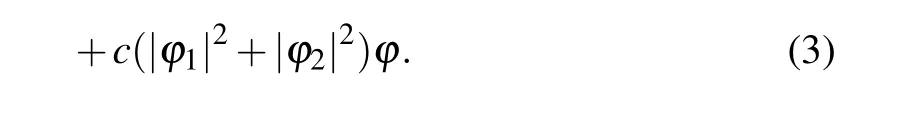
The energy spectrum of the above coupled nonlinear Schr¨odinger equation consists of this form of Bloch modeΨ(x,t)=φ(x)exp(ialtx-iμt),whereμrepresents the chemical potential. The above Eq.(3)can be applied for the case of very small reduced accelerated speedal.
3. Linear Bloch spectrum and Bloch waves
Gap solitons exist exclusively in the linear energy gaps,so it is significant to determine these band gaps. In order to achieve the band, we use the Bloch’s theoremφ(x) =un,k(x)exp(ikx) for the linear version of Eq. (3). Here,unkmeans a periodic function,kis the Bloch wave vector andnis the band index. The equation satisfied byunkis then in the form of

Figure 1(a) represents the linear Bloch spectrum of the real part of the eigenvalueμn,k. In the case of the integer wavenumber multipleq=1,q=2 andq=3, it is obvious to see that the curves almost overlap except the individual local part. Figure 1(b)is the spectrum of the imaginary part of the eigenvalue,and shows that the imaginary part of the eigenvalue is 0, which means the energy spectrum is totally real.When the depth of the imaginary part potentialv2increases to 2, the situation becomes different. As shown in Fig.2, the real parts of energy spectrum no longer overlap,and the imaginary parts of the eigenvalue have a non-zero value when the integer wavenumber multiples areq=2 andq=3,so thePTsymmetry is spontaneously broken.
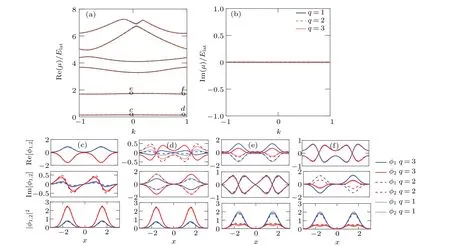
Fig.1. Linear Bloch spectrum and Bloch waves at the points of the spectrum. (a)and(b)The linear Bloch spectrum for the depth of imaginary part v2=0.3. The Bloch waves in the lowest two bands are stated in(c)–(f),the corresponding points shown in(a). Blue lines are for φ1,while red lines are for φ2. The other parameters Ω =1,δ =0.5,γ =1 and v1=6 remain the same in this paper.
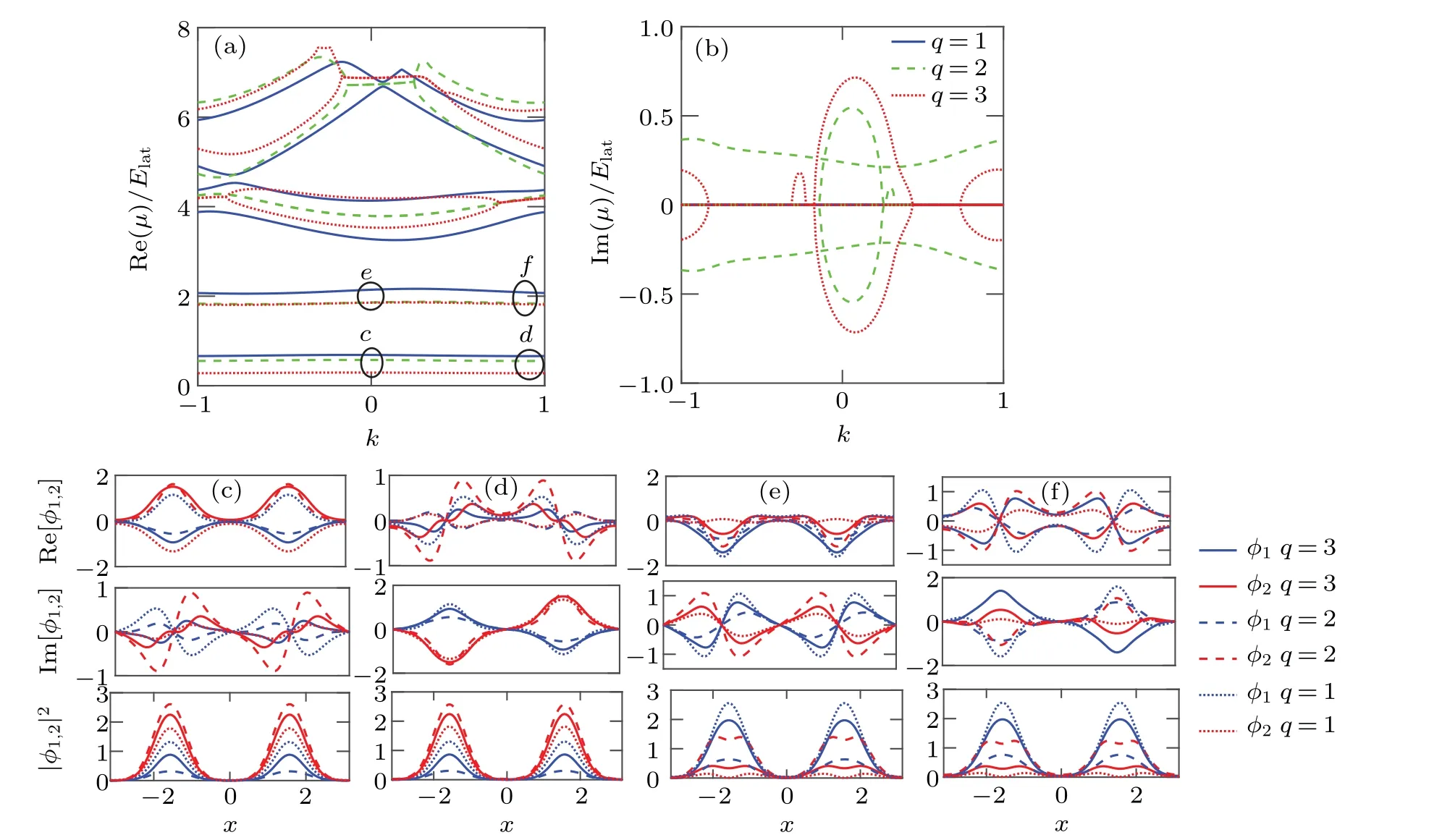
Fig.2. Linear Bloch spectrum and Bloch waves at the points of the spectrum. (a)and(b)The linear Bloch spectrum for the imaginary potential depth v2 =2. The Bloch waves in the lowest two bands are indicated in (c)–(f), the corresponding points shown in panel (a). The other parameters are identical to Fig.1.
In Figs.1(c)–(f),it can be observed that when the depth of the imaginary part potential isv2=0.3,the linear Bloch waves at the spectral symmetry mark points exhibit a weak spin polarization phenomenon. The first componentφ1dominates in the second band, and the second componentφ2dominates in the first band. In Figs. 2(c)–2(f), we show the results for the depth of the imaginary partv2=2. The spin polarization phenomenon of Bloch waves becomes more obvious for the different value ofq, while the spin polarization atk=0 andk=1 of the same energy bands maintains the same. We also analyze the change ofv2on the spectrum for the different integer wavenumber multipleq,as shown in Fig.3.It can be observed from the figure that in the case of the integer wavenumber multipleq=1, with the gradual increase of the depth of imaginary part potentialv2, the bandwidths of the first band gap and the second band gap gradually narrow. When the integer wavenumber multiple isq=2, the first band gap constantly narrows and the second band gap widens step by step. For the case of the integer wavenumber multipleq=3, the first two bands are separated totally with the increase ofv2.
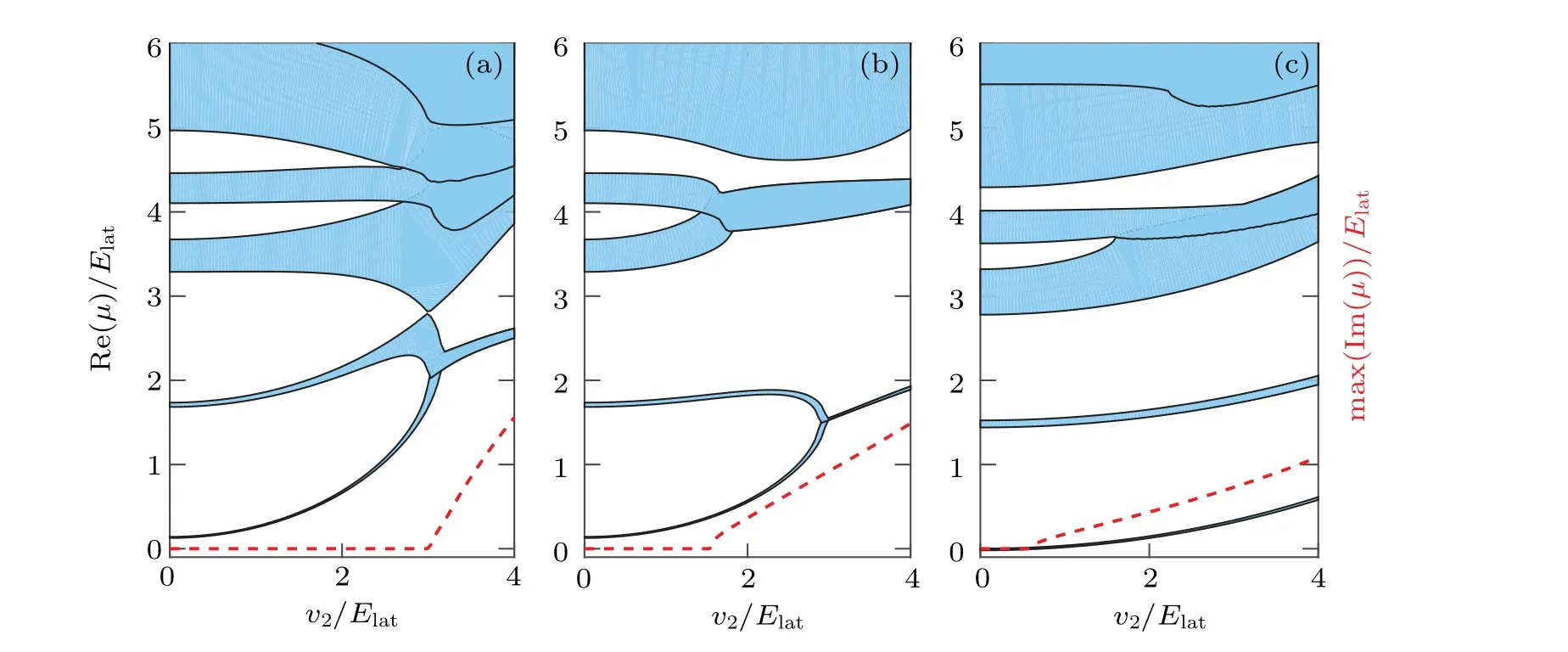
Fig. 3. Linear Bloch spectrum. The filled areas represent the energy bands, the blank areas represent the gaps. (a)–(c) The spectrum of the depth of imaginary part potential v2 for the integer wavenumber multiple q=1,q=2 and q=3,respectively.
It can be seen from the red dotted line in Fig.3 that when the integer wavenumber multiple isq=1, thePTsymmetry still exists in the intervalv2≤3,so the energy eigenvalue can have a completely real energy spectrum for the case.When the integer wavenumber multiple isq=2,the symmetry is maintained in the interval ofv2≤1.5. When the integer wavenumber multiple isq=3,the interval that satisfies thePTsymmetry is getting smaller and smaller. The above analysis results are in full agreement with Fig.2(b). We can conclude that the broken critical value ofPTsymmetry will gradually become smaller with the decrease of the period of the imaginary part potential. In the following content,we will study the existence of the gap solitons in the first band gap for the three cases(q=1,q=2,andq=3)in Fig.3.
4. Gap solitons
The Newton relaxation method is used to numerically calculate the gap soliton solutions of Eq.(3). First of all,we discretize Eq.(3), set the initial solution, and then fix the chemical potential in the band gap region with the zero boundary condition. The gap solitons of the first and second gaps in the case of the depth of imaginary partv2=0.3 andv2=2 have been described in Fig.4. In the first band gap region,there exists one family of fundamental single-peak band gap solitons,named as the first family solitons.[33]In addition, a class of high-order fundamental solitons are also found,which can be understood to advance from the fundamental mode to the composite mode,named as the double-peak gap solitons. With the increase of the depth of the imaginary partv2,both single-peak gap soliton modes and double-peak soliton modes have bigger norm than whenv2=0.3, and the norm of the double-peak gap solitons is always stronger than the one of single-peak gap solitons in the(N,μ)plane.

Fig.5. The density distribution of single-peak gap solitons in the first gap for the case of the integer wavenumber multiple q=1, q=2 and q=3. Here,the depth of imaginary part v2=0.3 is used in panel(a). In panel(b)the depth of the imaginary part is v2=2.
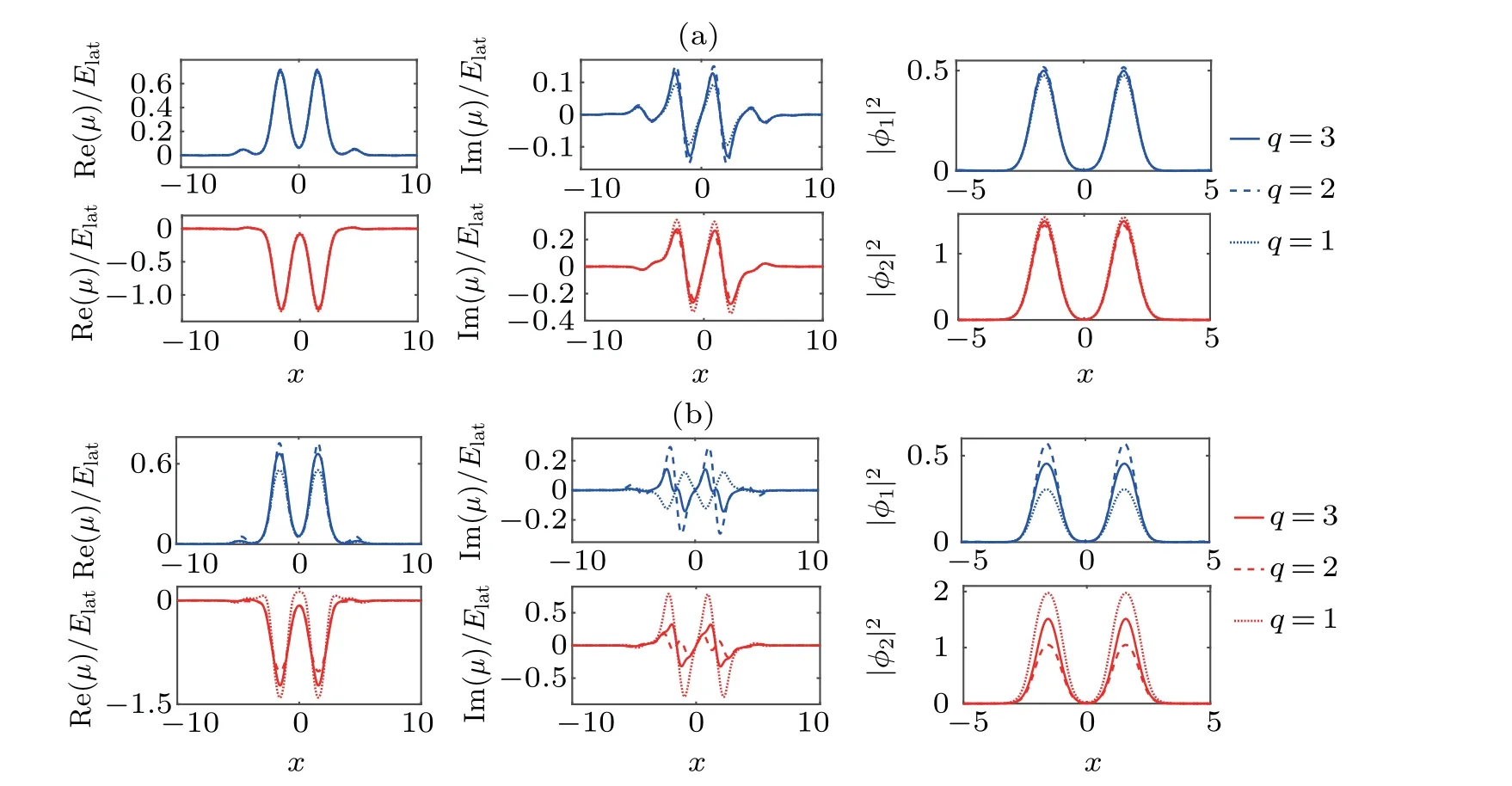
Fig.6. The density distribution of double-peak gap solitons in the first gap for the case of the integer wavenumber multiple q=1,q=2 and q=3. Here,the depth of imaginary part v2=0.3 is used in panel(a). In panel(b)the depth of the imaginary part is v2=2.
The density distribution of the single-peak gap solitons is shown in Fig. 5. It is very obvious that the single-peak gap solitons have parity symmetry in Fig.5(a). As the depth of the imaginary partv2increases to 2, the gap solitons transform into spin polarization, as shown in Fig. 5(b). Figure 6 shows the density distribution of double-peak gap solitons. We can see that this dipole mode is a composite structure comprising two modes of the same phase. When the depth of the imaginary part isv2=2, the double-peak gap solitons have also been polarized. It can be observed from Figs.5 and 6 that the amplitude of the gap solitons grows with the increase of the depth of the imaginary partv2, but the parity symmetry does not change.
5. Analysis of solitons stability
The stability analysis is crucial for the gap soliton solutions. Because it is about whether it is observable in the experiment. In this chapter,the influence of the depth and period of the imaginary part of thePT-symmetric potential on the stability of the gap solitons is mainly analyzed by using the split-step Crank–Nicolson method.[34]In order to excite the perturbation,a Gaussian random noise is superimposed on the gap solitons, then the overall waveform is used as the initial value and begins to evolve in Eq.(3). We first set the integer wavenumber multipleq=1 for the single-peak gap solitons family of the first band gap, and the stability analysis results are shown in Figs. 7(a) and 7(b). It can be clearly seen that when the depth of the imaginary part isv2=0.3,the first family gap solitons are linearly stable in Fig.7(a). As the depth of imaginary partv2increases to 2, the gap solitons are linearly unstable in Fig.7(b). The result is as the same for the doublepeak gap solitons as shown in Figs. 7(c) and 7(d). Dynamic evolution is stable for the depth of the imaginary partv2=0.3 and unstable forv2=2. Through precise analysis,it is found that this situation also applies to the integer wavenumber multiplesq=2 andq=3.

Fig.7. Time evolution of gap solitons in the first gap. The initial wave functions are the gap solitons solutions with Gaussian distributed noise added on. (a)A stable evolution of single-peak gap solitons in the first band gap at v2 =0.3. (b) An unstable evolution of single-peak gap solitons in the first band gap at v2 =2. (c) A stable evolution of double-peak gap solitons in the first band gap at v2=0.3. (d)An unstable evolution of double-peak gap solitons in the first band gap at v2=2. For all panels,the chemical potential is μ =1.
6. Conclusion
We have researched the properties of gap solitons in SOCBECs system withPT-symmetric potential.The linear energy spectrum and Bloch waves for the different depths and periods of the imaginary part ofPT-symmetric potential are carefully investigated. Two types of gap solitons are obtained numerically in the first band gap, namely, the single-peak gap solitons and double-peak gap solitons. The increase of the depth of the imaginary potential causes the two kinds of gap solitons to become spin-polarized notably and grow in amplitude.Finally, the method of the real-time evolution with the noise is used to analyze the dynamic evolution of the corresponding gap solitons. It is found that when the depth of imaginary part ofPT-symmetric potential increases,the gap solitons gradually become unstable. While the variation of the period of the imaginary part does not change the stability of the gap solitons for the parameter interval.
Acknowledgement
This work is supported by Science and Technology Project of Hebei Education Department, China (Grant No.ZD2020200).
- Chinese Physics B的其它文章
- Solutions of novel soliton molecules and their interactions of(2+1)-dimensional potential Boiti–Leon–Manna–Pempinelli equation
- Charge density wave states in phase-engineered monolayer VTe2
- High-pressure study of topological semimetals XCd2Sb2(X =Eu and Yb)
- Direct visualization of structural defects in 2D semiconductors
- Switchable down-,up-and dual-chirped microwave waveform generation with improved time–bandwidth product based on polarization modulation and phase encoding
- Machine learning potential aided structure search for low-lying candidates of Au clusters

