考虑源荷不确定性和相关性的关键线路辨识
王洪涛,邹 斌
(1.宁德师范学院信息与机电工程学院,宁德 352100;2.上海大学机电工程与自动化学院,上海 200444)
近年来,世界各地的大停电事故频发,起因往往是由单个元件故障或过载线路被切除引发潮流转移,引发连锁故障后导致大面积停电,威胁到电力系统的安全稳定运行[1]。因此关键线路辨识对预防电网连锁故障和制定大停电事故预案具有重要意义。
随着可再生能源发电量所占比例逐年升高,给电力系统注入了强不确定性,电力系统的运行状态复杂多变,因此在辨识关键线路时,需要考虑不同运行状态下线路潮流的影响。
目前关键线路辨识方法以确定运行方式下的潮流计算结果为基础,采用输电介数[2]、电气介数[3-4]、潮流介数[5-7]、功率介数[8]、综合介数[9]和传输介数[10]等指标衡量线路对功率传输中所起的作用,辨识电网中的关键线路。文献[2]以电网有向图模型为基础,搜索源流节点对间的潮流传输路径,从电网源流节点对输电能力的角度定义了输电介数,以输电介数为指标辨识关键线路。文献[3]计及不同发电容量与负荷水平的影响,基于电路方程,提出了电气介数指标,反映了线路在所有发电机与负荷节点对之间传输功率的权重。文献[4]在文献[3]的基础上引入发电机-负荷节点对的灵敏度因子,定义了计及灵敏度因子的加权电气介数,用于脆弱性线路辨识。文献[5-7]基于潮流计算,利用有功潮流追踪方法量化线路对发电机-负荷节点对的功率传输贡献,提出了潮流介数的概念,辨识关键线路。文献[8]引入线路功率介数的发电机因子、负荷因子及其权重系数,定义了线路功率介数,按功率介数的大小确定关键线路。文献[9]综合考虑了网架结构、电网运行状态、继电保护重要度、电压偏移情况、实际地理位置等因素的影响,定义了综合介数,用于关键线路辨识。文献[10]计及线路对无功潮流传输的作用,提出传输介数的概念,用于辨识关键线路。此外,混合流介数[11]和传输因子介数[12]等指标相继被提出。以上研究将电网的运行参数与介数相结合,从不同侧面研究了电网的结构特性和状态特性对关键线路识别的影响,研究成果对电网规划和风险评估具有指导意义。
但以上研究均是在确定的电力系统运行方式下展开的,由于传统的电力系统中不确定因素主要源于负荷或季节性水电出力的不确定性[13],电力系统的运行方式相对固定,以某种典型运行方式下的潮流为基础进行关键线路辨识对传统的电力系统(未接入可再生能源)而言是适合的。
在高比例可再生能源接入电力系统的背景下,源荷两端的不确定性加剧,系统的运行方式呈现多样化,电网潮流双向化[13],因此在关键线路辨识时需要考虑源荷不确定性对系统运行状态的影响。文献[14]以静态安全裕度为指标,对交直流混联电力系统的关键线路辨识进行了研究,取得了良好的效果,但未考虑可再生能源出力的随机性对关键线路辨识的影响。文献[15]考虑了负荷随机波动、电网参数不精确和脆弱性模型选择的不确定性对电网脆弱性的影响。文献[16]计及了风电出力、负荷不确定性对关键线路辨识的影响,但未计及风电出力与负荷的相关性。文献[17]以线路负载率对潮流熵进行了改进,以综合潮流指标关键线路进行辨识,但仅考虑了风电出力的不确定性,未考虑多风电场出力相关性对辨识结果的影响。文献[18]以C藤Copula模型描述风电出力与多个区域负荷的不确定性和相关性,评估线路的过负荷风险,但C藤Copula的藤结构是固定的,且二维Copula函数的类型有限,会影响到建模的精度[19]。
在高比例可再生能源并网的背景下,为了发现潜在的关键线路,首先需要准确地模拟每个时间断面上系统的运行状态,要模拟每个时间断面上系统的运行状态就需要建立源荷概率模型,描述源荷的不确定性和相关性,获得源荷相关性样本;然后将源荷相关性样本用于概率最优潮流计算,获得每个时间断面上系统的运行状态(包括线路潮流的方向和大小),通过综合各种运行状态下线路的潮流介数,发现潜在的关键线路,实现关键线路辨识。
为此,本文以概率潮流介数为关键线路辨识的评价指标,采用BN(Bayesian network)建立源荷概率模型,描述风电出力、光伏出力与负荷的不确定性和相关性,以源荷相关性样本为基础进行概率最优潮流计算,然后利用顺流潮流追踪法,计算出线路的概率潮流介数,进而得到关键线路辨识结果。以IEEE 39节点系统为算例,将本文方法与静态辨识、计及源荷不确定性不计及相关性、计及源荷不确定性和相关性的关键线路辨识结果进行对比分析,对比结果检验了所提方法的有效性。
1 源荷概率模型
1.1 BN基本原理
基于概率推理和图论的BN通过结点(随机变量)间的条件概率表示随机变量间因果关系,同时可以在有限的、不确定性信息中进行学习与推理,计算多维随机变量的联合概率,能够描述各随机因素之间因条件相关性而产生的不确定性[20]。
设w个随机变量X={X i}i=1,2,…,w,BN包括两部分:一是描述随机变量间因果关系的网络结构W,二是度量随机变量间关系强度的分布参数(条件概率表)θ。
假设对Xi做o次采样,得到的数据样本集D={D1,D2,…,D o},通过BN的结构学习和参数学习后建立了一个BN=(G,θ),根据BN的链式规则可知,X={Xi}i=1,2,…,w的联合概率分布可以表示为
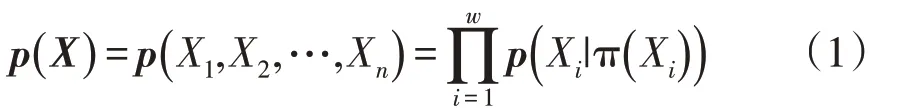
式中,随机变量X i所有父结点的集合用π(Xi)表示。
由于BN能够将多维随机变量的联合概率分布以概率图模型的方式表达,并有效地简化了联合概率分布的计算,得到多维随机变量的联合概率分布相当于获得了多维随机变量的全景式描述。因此建立源荷的概率模型,为高比例可再生能源背景下模拟系统的运行状态奠定了基础。
1.2 评分搜索的BN结构学习
评分搜索法是将BN的结构学习视为已知观测样本下的网络结构优化问题,因此先定义网络结构的评分函数,然后根据观测样本对每个候选网络结构进行评分,最后以评分最高的网络结构作为最优的结构[21]。
(1)评分函数
评分函数一般为带惩罚项的最大似然评分函数,最大似然函数反映了观测样本经验分布与候选结构的拟合程度,惩罚项对复杂的网络结构施加惩罚,防止网络结构对观测样本的过拟合。观测样本为离散数据时,网络结构的评分函数表示为

式中:D表示N个观测样本的离散数据集;W表示网络结构;̂为参数向量;i=1,2,…,w表示结点;j=1,2,…,q i表示结点Xi的父结点π(X i)的状态;k=1,2,…,r i表示结点Xi的状态;N ij代表观测样本中满足结点Xi的父结点π(Xi)为第j个状态值的样本个数;N ijk代表观测样本中满足结点X i的父结点π(Xi)为第j个状态值且结点Xi为第k个状态值的样本个数。
带惩罚项的评分函数表示为

式中:f(N)是与观测样本个数N有关的非负惩罚函数;dim(W)表示网络结构W的复杂度。
(2)结构搜索
在确定了网络的评分函数后,BN网络的结构学习就转换为依据观测样本寻找最优网络结构。爬山法是基于评分函数的经典算法[22],该方法先从任意一个初始网络结构开始,然后对网络进行边操作(加边、减边、边翻转),局部修改网络结构,得到一系列的候选网络结构,再用评分函数对每个候选网络结构进行评分,从候选网络结构中筛选出最优的候选网络结构。将最优的候选网络结构与初始网络结构进行评分比较,如果最优的候选网络结构评分高于初始网络结构,则将最优的候选网络结构作为初始网络结构开始下一轮搜索;否则,停止搜索,将初始网络作为最优网络的结构,作为BN网络学习的结果输出。
1.3 最大似然估计法的BN参数学习
参数学习是在已确定BN网络结构的基础上确定结点与结点间的连接强度,即是对结点间的条件概率表进行估计。在观测样本量较大,观测样本较为充足时,最大似然估计法的参数学习精度较高[23]。
在BN的网络结构已知的情况下,需要估计的BN网络参数为

记θ是由θijk组成的向量,则θ的似然函数为

式中,D l为D中第l次采样(或观测)的样本,l=1,2,…,h为采样次数。
式(6)两边取自然对数,得到对数似然函数
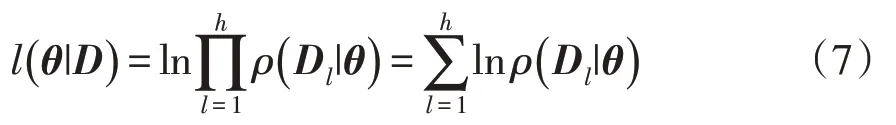
对式(7)求极值,即可得到θijk的最大似然估计量。
经过BN结构学习和参数学习后,就能够建立基于BN的源荷概率模型,该模型以联合概率分布的形式准确、全面、完整地描述了源荷的不确定性和相关性。
需要说明的是,对于服从任意分布的多维连续型随机变量而言,在建立BN模型时需要对连续型随机变量做离散化处理,建立BN模型后按照从根结点到叶子结点进行遍历采样,得到随机变量的离散的概率值样本,将该样本做连续化处理和累积概率分布的逆变换,获得服从多维随机变量联合概率分布的连续型样本,具体方法见文献[24],这里不再赘述。
2 线路的潮流介数与概率潮流介数
2.1 线路的潮流介数
在电网中,电源节点发出的功率经过线路传输到负荷节点,由于电源节点和负荷节点在网络拓扑中的位置不同,同一个电源节点向不同的负荷节点传输功率时所经过的线路不同,同一负荷节点从不同的电源节点汲取功率时所利用的线路也不相同,因此电网中各电源节点同时向各负荷节点传输功率时,在每条线路上流过的功率不同、每条线路的利用程度不同、每条线路在系统中的重要性也不同。
为了表征电源m向负荷n输送功率P(m,n)时每条线路在全网中的利用程度和重要性,定义单一电源-负荷节点对的线路潮流介数[5]为
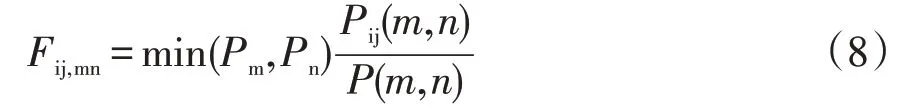
式中:min(Pm,Pn)为单一潮流介数的权重,取电源m的实际有功出力与负荷n的实际有功负荷中的较小值;P(m,n)为电源m向负荷n传输的有功功率;Pij(m,n)为电源m向负荷n传输有功功率P(m,n)时对线路ij上潮流的贡献功率;Fij,mn可以表征单电源向单负荷传输有功功率时,全网所有线路的重要程度。
按式(8)可计算出每条线路的Fij,mn,根据叠加原理,将所有电源-负荷节点对在传输有功功率时线路的潮流介数累加,可得到线路潮流介数Fij为

式中:m为电源节点;G为电源节点集;n为负荷节点;L为负荷节点集。
由于线路潮流介数Fij不仅与电源、负荷的实际出力有关,而且与系统运行状态、网络拓扑结构有关,因此Fij反映了线路ij在功率传输过程中的贡献和重要程度,可以作为关键线路辨识的评价指标。
2.2 基于潮流追踪法的线路潮流介数计算
在线路潮流介数的表达式(9)中,需要获得P(m,n)以及Pij(m,n)。根据潮流追踪[5,16,25]的原理,在确定电网潮流分布的情况下,将网络简化为无损网络,然后构造顺流分配矩阵,采用顺流追踪法对电源-负荷节点对的潮流进行追踪,确定线路ij中的功率组成分量,具体计算方法如下。
(1)在确定电网运行状态的情况下,得到发电机发出有功功率、负荷吸收的有功功率、各条线路的有功潮流和线路损耗。
(2)电网潮流无损化处理。将线路有功损耗作为等效负荷,均摊至线路的首端和末端节点,形成有功无损网络。
(3)基于有功无损网络构造顺流分配矩阵A=(aij)r×r,r为网络中的节点个数,矩阵中的元素a ij为
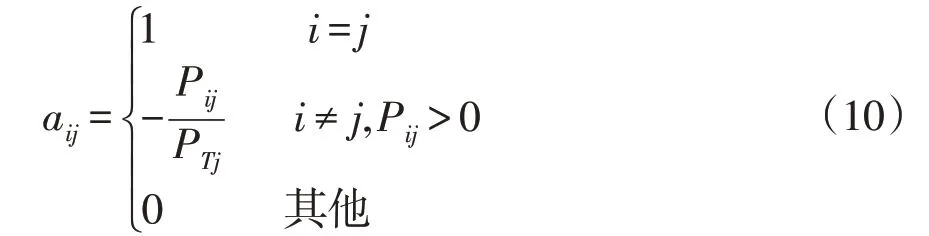
式中:P ij为线路ij从i节点流向j节点的有功功率;PTj为节点j总注入的有功功率。
(4)构造发电机有功出力对角阵PGG、节点有功负荷对角阵PLL和节点注入有功功率对角阵PTT
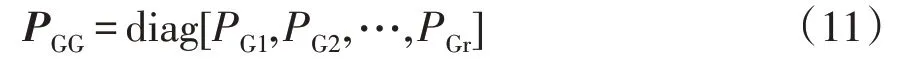
式中,PGr为节点r的发电机有功出力。

式中,PLr为节点r的有功负荷。
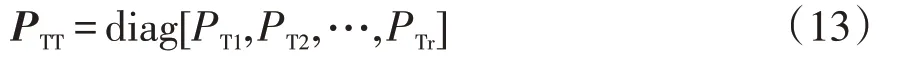
式中,PTr为节点r注入的总的有功功率。
(5)计算电源节点向负荷节点分配有功功率的系数矩阵KG和负荷节点从电源节点汲取有功功率的系数矩阵KL

(6)求取电源节点m向负荷节点n提供的有功功率P(m,n)为

式中:KL(n,m)为有功汲取系数矩阵KL中第n行、第m列的元素;PGm为发电机节点m的有功出力。
(7)计算Pij(m,n)的关系式为

式中:i为线路有功功率流入的节点号;j为线路有功功率流出的节点号;KL(n,j)为矩阵KL中第n行、第j列的元素,KG(m,i)为矩阵KG中第m行、第i列的元素;Pij为线路ij上的有功功率。
(8)根据式(9)计算出电网中所有线路的潮流介数Fij。
2.3 线路的概率潮流介数
为了考虑源荷的不确定性引起系统运行状态的变化,以概率最优潮流计算为基础,计算线路的概率潮流介数。在忽略风电和光伏机组发电成本的情况下,将最优潮流的目标函数设置为常规机组的发电成本,约束条件包括有功功率和无功功率的平衡约束、常规发电机有功出力和无功出力的上下限约束以及节点电压幅值的上下限约束。最优潮流采用原对偶内点法求解,求解后确定系统的运行状态,再根据顺流潮流追踪法,计算每条线路的潮流介数。
假设风光荷样本的集合中共有N组样本,若第k组样本对应的最优潮流收敛,此时系统的运行状态为k,以该状态下所有线路的潮流介数中的最大值max(Fij(k))为基准值,将每条线路的潮流介数归一化为

运行状态k出现的概率为

式中,Ns为N组样本中最优潮流收敛的总次数。
根据式(18)和(19)可定义线路i j的概率潮流介数Ri,j为

概率潮流介数Ri,j实质上是线路ij在各种运行状态下潮流介数的期望,它综合了电网运行状态和线路潮流介数两方面的因素,既反映了运行状态出现的概率,也体现了线路在该运行状态下对功率传输的贡献。
2.4 关键线路辨识流程
考虑源荷不确定性和相关性的关键线路辨识流程图如图1所示,具体步骤如下:

图1 关键线路辨识流程Fig.1 Flow chart of critical line identification
(1)输入电网原始数据和风电、光伏出力以及负荷的全年每小时数据;
(2)以BN建立源荷概率模型,采用蒙特卡洛抽样法从概率模型中抽样得到N组样本负荷、光伏出力和风电出力的相关性样本;
(3)设置k=1,以第k组样本为基础进行最优潮流计算;
(4)如果最优潮流收敛,则进入下一步;否则,返回上一步,取k+1组样本进行最优潮流计算;
(5)以最优潮流计算结果为基础,进行顺流潮流追踪,计算线路的潮流介数;
(6)判断N组源荷相关性样本是否全部用于最优潮流计算如k<N,则k=k+1,返回到步骤(3),取k+1组源荷相关性样本进行最优潮流计算;如k=N,则进入下一步。
(7)计算所有线路的概率潮流介数,按概率潮流介数对关键线路排序。
3 算例研究
3.1 源荷概率模型
以美国PJM市场公布的2017年MIDATL区域负荷、4个光伏电站出力和4个风电场出力的全年每小时数据作为BN建模数据[18]。各连续型随机变量的离散化区间的个数为[3 3 4 6 3 3 5 4 6 3],采用基于评分函数的爬山法和最大似然估计法对BN进行结构学习和参数学习,图2给出了经过BN结构学习和参数学习后得到的网络结构图。
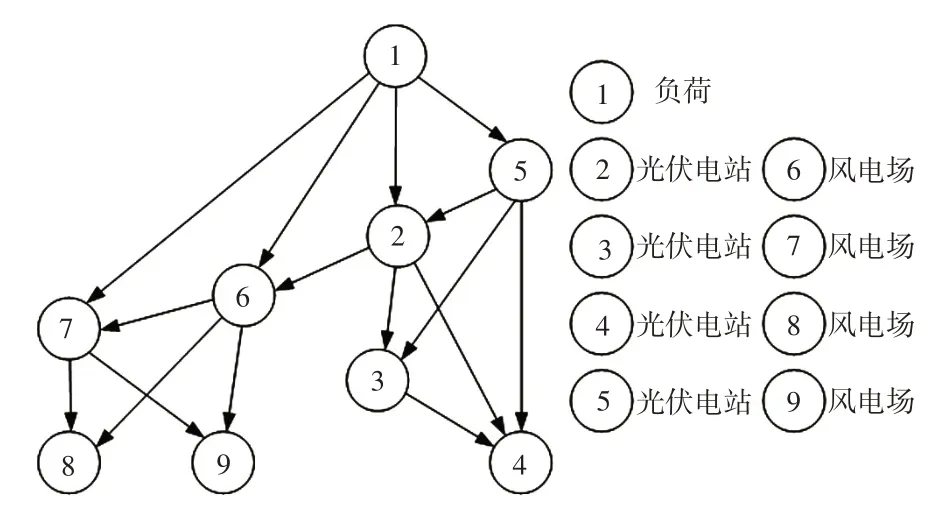
图2 贝叶斯网络结构Fig.2 Structure of Bayesian network
由BN结构图2可见该区域的负荷与风电出力、光伏出力之间有相关性,通过参数学习可以获得网络结点间的条件概率表,条件概率表定量表达了结点之间的相关性。以6#结点为例,表1给出的条件概率表反映了6#结点与1#负荷结点、2#光伏结点之间的条件依赖关系,表中“La”、“So”、“Wi”分别表示1#负荷、2#光伏出力和6#风电场出力的状态,状态值“1”、“2”、“3”表示负荷(或光伏出力、风电场出力)处于“低”、“中”、“高”三类状态。
以表1中最后一行第一列的数据为例,说明条件概率表中数据的含义,表中“La=3,So=3”表示如果负荷、光伏出力都处于“高”的状态下,风电场出力处于“低”状态的概率为0.630 6,即:ρ(Wi=1|La=3,So=3)=0.630 6,表中其他条件概率值的含义与此相同。

表1 6#风电场出力(Wi)与1#负荷(La)、2#光伏出力(So)的条件概率Tab.1 Conditional probabilities of No.6 wind farm output(Wi),No.1 load(La)and No.2 photovoltaic output(So)
对所建立的BN概率模型,按照网络结构图中的条件依赖关系,从根结点(图2中的1号结点)至叶子结点进行顺序采样。每次采样时,先给出根结点的实例化取值(实例化取值由根结点的离散分布律决定,如:ρ(La=1)=0.2,ρ(La=2)=0.5,ρ(La=3)=0.3),然后根据BN的条件概率表得到叶子结点的实例化取值。采样1 000次后,就得到1 000组离散的概率值样本,利用式(21)将每个离散的概率值转换为连续的概率值,再通过各维随机变量累积概率分布的逆变换,得到各维随机变量的样本,即为源荷相关性样本。

式中:a、b表示离散的概率值对应的连续区间左右端点值;rand为均匀分布的随机数。
为比较是否考虑源荷不确定性和相关性的样本差异,给出4种情况下对应的样本为
Case1:负荷、光伏出力和风电出力的8 760 h时序样本,简称“原始样本”。
Case2:风光荷相互独立,以两参数的Weibull分布描述风电出力,采用Beta分布描述光伏出力,Weibull和Beta分布的参数通过对原始数据的参数估计得到;以正态分布描述负荷,正态分布的均值、标准差为原始样本的均值、标准差。分别对Weibull分布、Beta分布和正态分布进行蒙特卡洛抽样1 000次,获得的样本,简称“独立样本”。
Case3:考虑风光荷的不确定性和相关性,采用C藤Copula概率模型[19,26-27],建立源荷概率模型,对模型抽样1 000次得到的样本,简称“Copula样本”。
Case4:考虑风光荷的不确定性和相关性,以BN建立源荷概率模型,抽样1 000次得到的相关性样本,简称“BN样本”。
4种负荷样本的概率密度曲线如图3所示,比较4种负荷样本的概率密度曲线可见:独立样本与原始样本的概率密度曲线相比差异较大,其原因是该区域的实际负荷并不严格服从正态分布,以理想的正态分布描述该区域负荷,则产生了较大的偏差。Copula样本、BN样本的概率密度曲线与原始样本的概率密度曲线吻合度高,在峰值处BN样本比Copula样本的概率密度曲线更贴近原始样本的概率密度曲线。
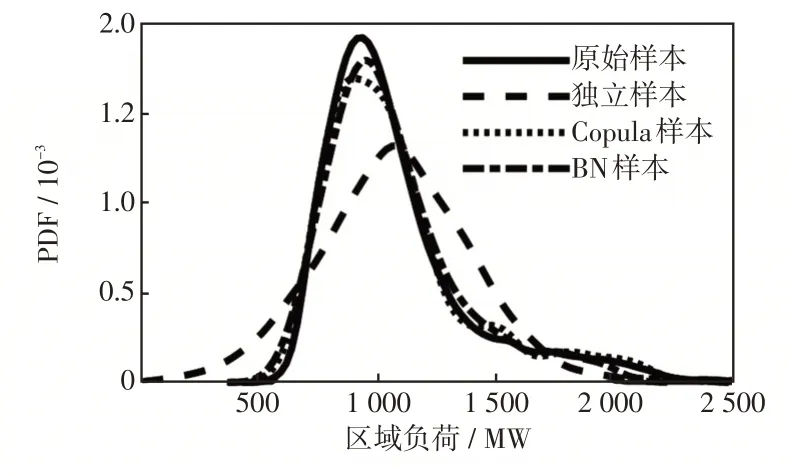
图3 区域负荷概率密度Fig.3 Probability density of regional load
2#光伏出力样本的概率密度如图4所示,将独立样本、Copula样本、BN样本与原始样本的概率密度比较可知,BN样本的概率密度曲线更接近原样本概率密度曲线。8#风电出力样本的概率密度如图5所示,独立样本与原样本的概率密度曲线大体一致,Copula样本、BN样本与原样本的概率密度曲线基本吻合,相比较而言BN样本的吻合度更高。
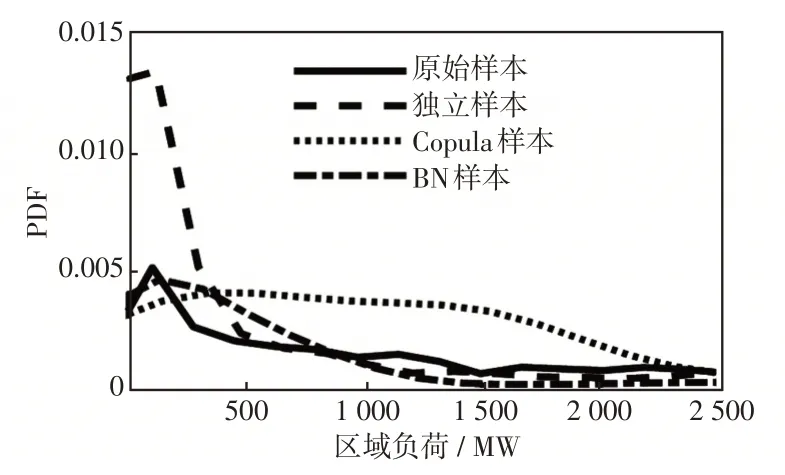
图4 光伏电站出力的概率密度Fig.4 Probability density of output from photovoltaic power station

图5 风电场出力的概率密度Fig.5 Probability density of output from wind farm
4种样本归一化后的均值和标准差如图6和图7所示,从图6和图7中可见独立样本的均值、标准差与原始样本的差异最大,BN样本与原样本的均值、标准差基本相同。
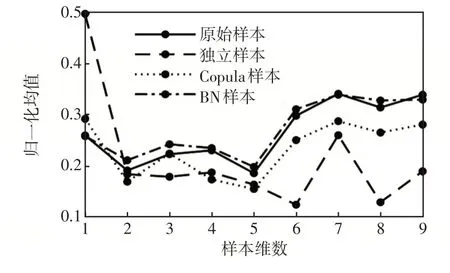
图6 样本的归一化均值Fig.6 Normalized mean of samples
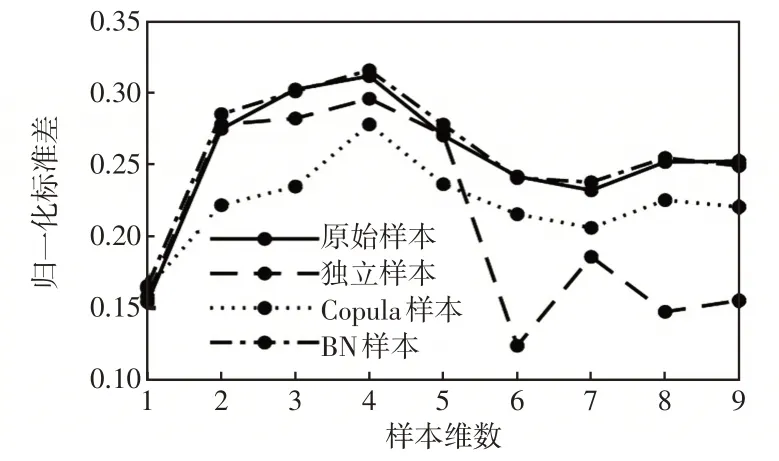
图7 样本的归一化标准差Fig.7 Normalized standard deviation of samples
综合以上比较和分析,说明通过BN建立的概率模型能够描述风电、光伏出力与负荷的相关性,蒙特卡洛抽样得到的BN样本基本再现了原始样本的概率特征。Copula样本与原始样本的概率特征基本一致,由于C藤Copula采用了固定的藤结构,且二维Copula函数的类型有限,影响了模型的精度[19]。独立样本由于没有考虑风光荷的相关性,该类样本与原始样本概率特征的差异较大。获得了相互独立的源荷样本和具有相关性的源荷样本,为是否计及源荷不确定性和相关性的关键线路辨识奠定了基础。
3.2 关键线路辨识
以IEEE 39节点系统为测试系统[28],系统中发电机14台、负荷节点19个、线路46条,系统总负荷6 254 MW,发电机有功出力6 297.9 MW。4个风电场和4个光伏电站分别接入21、32、34、38节点和8、24、35、39节点,修改后的系统接线如图8所示。4个风电场额定功率分别为200 MW、150 MW、100 MW、100 MW,4个光伏电站额定功率均为50 MW,风电、光伏电站接入的额定有功功率之和为750 MW。将Case1~Case4的样本分别做归一化处理,然后将各维风电、光伏样本乘以各风电场、光伏电站的额定有功功率,就获得了各风电场、光伏电站的实际有功出力。按恒功率因数cosφ=0.98可以得到风电场、光伏电站的无功功率。系统总负荷在原系统总负荷的基础上增加30%,再乘以MIDATL地区实际负荷归一化系数,作为修改后的节点负荷。
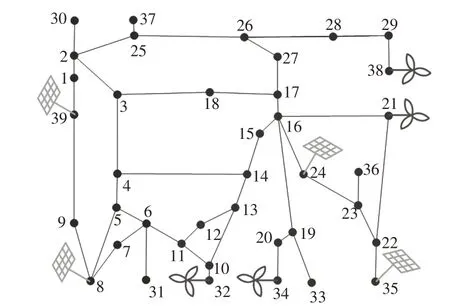
图8 IEEE 39节点系统Fig.8 IEEE 39-node system
将3.1节Case1~Case4得到的4种样本做尺度变换后,进行概率最优潮流计算,得到各种情况下按概率潮流介数排序的关键线路辨识结果如表2所示(取每种情况下排名前十的线路)。表2中静态辨识是不考虑源荷不确定性情况下的关键线路辨识结果;Case1是以风光荷原始样本为基础得到的关键线路辨识结果,以Case1作为其他关键线路辨识的比较标准。Case2是以独立样本为基础的得到的关键线路辨识结果;Case3是以C藤Copula为基础的得到的关键线路辨识结果;Case4是以BN样本为基础的得到的关键线路辨识结果。

表2 按概率潮流介数排序的关键线路辨识结果Tab.2 Critical line identification results sorted by probabilistic power flow betweenness
比较表2中静态辨识与Case1的辨识结果可见,不考虑风光荷不确定性与既考虑风光荷不确定性又考虑相关性的关键线路辨识结果差异性显著,静态辨识Ri,j排序前十的线路中只有6条线路与Case1的相同,误判率为40%。说明在可再生能源并网、负荷随机波动的情况下,静态辨识难以发现电网中全部潜在的关键线路,辨识的误判率高。
Case1~Case4为考虑源荷不确定性的辨识,以Case1的辨识结果为参考标准,其他3种情况与Case1的结果进行比较可见,Case2考虑风光荷的不确定性但不考虑相关性,排序前十的关键线路中有两条线路(25-37和16-24)与参考标准不一致,关键线路辨识的误判率为20%,辨识误差较大。Case3和Case4得到排序前十的关键线路与Case1相同,但排序和概率潮流介数与Case1有差异。
以Case1、Case3和Case4辨识结果中排序前三的线路16-17、21-22、23-36为例进行分析。
(1)线路16-17:该线路在Case3和Case4的辨识结果中排在第1位,在21号、24号、34号、35号节点分别接入风电、光伏机组后,线路16-17成为功率外送的枢纽,风电、光伏出力通过该线路向其他节点输送,电源-负荷节点对传送功率经过该线路的次数显著增加(潮流介数的广度),电源-负荷节点对在该线路上引起的有功分量增加,因此概率潮流介数R16,17最大,静态辨识和Case1-Case4的辨识结果都验证了这一结论。
(2)线路21-22:该线路在Case4中排在第2位,与Case1的排序相同,该线路Case4与Case1的Ri.j值相比,相对误差为3.33%,相对误差较小。在Case3中该线路排在第3位,该线路Case3与Case1的Ri,j值相比,相对误差为7.78%,相对误差较大,说明Case4比Case3的辨识精度高。线路21-22是风电、光伏出力的外送和联络线路,是系统中的关键线路,该线路在静态辨识结果中排序为第8,说明高比例可再生并网后,该线路的重要性显著上升。
(3)线路23-36:该线路是连接常规发电机和风力机组的线路,Case2和Case3中该线路排在第2位,Case4中排在第3位与Case1的排序一致,说明Case4的辨识结果更准确。
为了进一步比较4种不同情况下概率最优潮流计算的结果,图9给出了16节点的电压幅值的PDF和线路16-17的有功潮流,从图9(a)可见,Case2不考虑风光荷相关性的情况下,16节点的电压PDF与Case1相比有较大差异,Case3和Case4的PDF与Case1的PDF差异较小。图9(b)中,Case3和Case4情形下线路16-17的有功潮流PDF与Case1的基本吻合;Case2情形下的有功潮流PDF与Case1的有显著性差异。

图9 节点电压幅值和有功潮流的概率密度Fig.9 Probability density of node voltage amplitude and active power flow
16号节点电压幅值均值和标准差如表3所示,线路16-17有功潮流的均值和标准差如表4所示。比较表3、表4中Case1~Case4的均值、标准差和相对误差可知:Case4情形下电压幅值和有功潮流的均值、标准差相对误差最小、Case3的相对误差次小,Case2的相对误差最大。比较结果表明,以BN样本为基础的概率最优潮流计算结果与原始样本(时序的)为基础的概率最优潮流计算结果最为接近,说明所提方法能够较为准确地模拟高比例可再生能源接入后电网的运行状态。
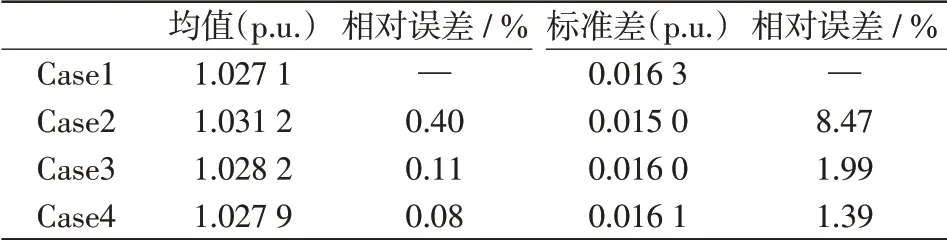
表3 16号节点电压幅值的均值、标准差Tab.3 Mean and standard deviation of voltage amplitude at Node 16
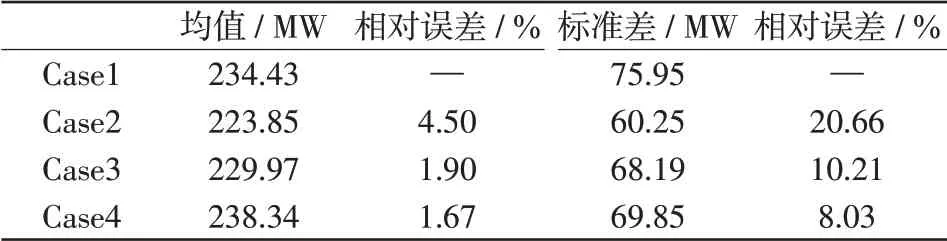
表4 线路16-17有功潮流的均值、标准差Tab.4 Mean and standard deviation of active power flow of line 16-17
Case1~Case4情形下4种样本的概率最优潮流收敛次数如表5所示,由表5可知:4种风光荷样本进行最优潮流计算,最优潮流收敛的次数均大于各自样本组数的90%,说明概率最优潮流基本实现了对风电出力、光照强度、负荷不同取值状态下系统运行状态的模拟,概率最优潮流的模拟结果为关键线路辨识提供了完整、可靠的系统运行数据,关键线路辨识结果的可信度高。

表5 概率最优潮流的收敛次数Tab.5 Number of convergence of probabilistic optimal power flow
4 结论
高比例可再生能源并网后使得电力系统的运行方式复杂多变,状态变量随运行方式的改变而时刻变化,确定运行方式下的关键线路辨识方法无法考虑源荷不确定性和相关性对辨识结果的影响。为此,本文提出了考虑源荷不确定性和相关性的关键线路辨识方法。该方法利用基于BN的源荷概率模型,将概率最优潮流与顺流潮流追踪法相结合,以概率潮流介数为指标对关键线路进行辨识。以IEEE 39节点系统为算例,比较和分析了是否考虑源荷不确定性和相关性对关键线路辨识结果的影响,得到以下结论。
(1)不考虑源荷不确定性的关键线路静态辨识方法不适用于高比例可再生能源接入电网后的关键线路辨识,关键线路辨识的误判率为40%,误判率高。
(2)仅考虑源荷不确定性,不考虑源荷相关性的关键线路辨识方法的误判率为20%,辨识误差较大。
(3)本文方法和基于C藤Copula的关键线路辨识方法都能够同时考虑源荷不确定性和相关性,两者的前十条关键线路与参考标准一致,但前者的关键线路排序和线路概率潮流介数的精度高于后者。
(4)所提方法较为全面地反映了源荷不确定性和相关性对关键线路辨识的影响,辨识结果准确、可信度高,能够模拟复杂多变的电网运行状态,为开展预防电网连锁故障和制定电网事故预案等方面的研究提供了指导和参考。

