基于智能电表量测的低压配电线路参数辨识

黄璐涵，熊尉辰，宋晓林，宋国兵

（1.国网陕西省电力公司营销服务中心，西安 710054；2.西安交通大学电气工程学院，西安 710049）

据统计，电力系统80%以上的故障发生在配电网，其中一半以上的故障发生在低压配电网[1]。低压配电网发生故障后，一般由用户进行信息上送，再由技术工人排查故障线路，耗费人力物力，且目前针对其故障预测及定位的研究极少[2]。经过分析西安供电公司2019年第二季度的4 000余条历史抢修工单，发现超过50%的故障是由于触点氧化、虚接、线路老化等引起的非突发性故障，而绝大部分非突发性故障的发生都会伴随线路阻抗逐渐增大的现象。因此，可通过监测线路阻抗值，达到非突发性故障预测以及高危线路定位的目的。

相较于配电网，输电网中含有大量的相量测量单元及录波装置，测点数量占比大、测量信息更加完备。可以利用相量测量单元的数据估计输电线路参数[3-5]，也可利用录波数据求取线路参数[6]。但低压配电网支路繁多，考虑到其结构特殊性及建设成本，大量安装这些装置的可能性很小[7]，所以无法参考输电网的线路参数识别技术。

智能电表是在低压配电网中广泛应用的测量元件。截至2018年，智能电表在国家电网公司用户中覆盖率达到99.57%[8]。智能电表可上传带有时标的负荷计量值，如用电量、功率、电压、电流等[9-12]。虽然智能电表所提供的数据均为标量，不包括相位信息，但其隐含着拓扑的电气关系。解决利用标量信息进行线路参数计算的问题，对于电网公司节省检修成本、提高运维效率有着重要意义。

目前相关研究已有初步进展。文献[13]建立了单相低压配电网回路电阻模型，利用电压变化量与电流变化量的比值近似估计配电网的运行状态，且其假设条件十分苛刻，在工程中难以实现。文献[14]也建立了单相电阻模型，通过线性规划算法，利用电压、电流有效值及有功功率估计变压器二次侧线路电阻值，未考虑无功功率对计算的影响，与实际工况不符。

文献[15-17]在文献[14]的基础上搭建了单相线路阻感模型，采用的方法均为利用测量所得电压、电流有效值以及有功、无功功率，形成从各负荷处推得的电源电压关于线路阻抗的矩阵，通过二次规划优化算法寻找最合适的阻抗配置，较准确地求取了线路阻抗。但该算法所需的优化时间过长，不适用于大型电力系统。其中文献[17]较为详细地说明了所用算例情况，该算例为单相变压器带单相负荷模型，包含17个负荷电表节点、21条支路，运用所提方法求解其拓扑参数花费了2.75 h，耗时极长，显然不满足实际电力系统的计算需求。若未来想要在文献[17]的基础上进行适用于实际三相四线制低压配电网的扩展研究，难度很大。

为方便说明算法，本文以一种改进的单相低压配电线路模型为例进行分析，根据测量所得标量与拓扑参数的相关性，提出了兼具求解精度与求解速度的计算方法。首先给出线路阻抗初值，从负荷侧倒推得到各条线路的功率分布；再从电源侧正推，得到以电源电压为参考的各电气量，并将负荷处测得的电压电流有效值与正推得到的相角相结合形成新的负荷相量；然后将线路阻抗新值作为待求量，列写关于新的电气量与线路阻抗新值的KVL方程，并利用最小二乘法求解；最后将求解出的线路阻抗新值作为线路阻抗初值重新进行计算，形成迭代过程，可得到不断逼近阻抗真值的解。并在无附加测量误差及附加测量误差的情况下给出了相应的计算结果。

1 低压配电线路模型

为保证供电质量，低压配电变压器的供电半径一般不超过0.5 km。对于电压等级低的短线路，电容电流较小，常常忽略分布电容的影响，所以本文采用集中参数RL线路模型。

考虑到变压器出口后一般均有分支存在，在文献[15]的基础上将拓扑扩建为含有两大分支的结构，建立单相变压器带单相负载的线路模型，如图1所示。值得说明的是，本文方法同样适用于任意辐射状的低压配电网拓扑结构，在此为方便使用公式说明，以文献中常用的拓扑形式为例进行分析。

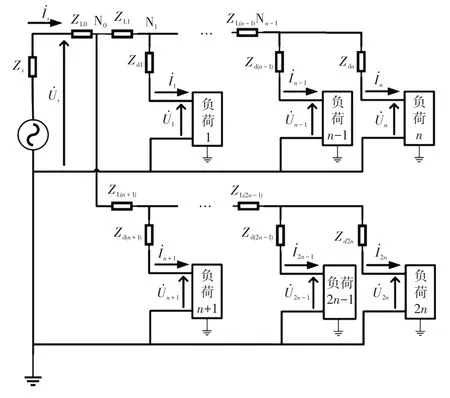
图1 低压配电线路模型Fig.1 Model of low-voltage distribution lines

将变压器二次出口处等效为电源，图1中：Us、Is为等效电源的电压、电流有效值；Zs为电源等效阻抗。

已知量为智能电表测得量：

（1）电源处（即总表处）电压有效值Us、电流有效值Is、有功Ps、无功Qs；

（2）各负荷处电压有效值Uj、电流有效值Ij、有功P j、无功Q j，其中j=1，2，…，2n。

为简明，在图1中未标出测得功率的符号。智能电表可不断地采集并上送这些数据，用户数据的大量获取使得利用测量量进行线路参数计算成为可能。

待求量为各线路阻抗：

（1）电源出口处一级干线阻抗ZL0（因电源处有总表测点，需要有一条线路承载总表，这里将该线路阻抗命名为一级干线阻抗ZL0，其后的分支点（中间节点）命名为N0）；

（2）已有分支节点的二级干线阻抗ZLi，其后的分支点（中间节点）命名为N i，其中i=1，2，…，n-1，n+1，…，2n-1；

（3）负荷支路阻抗Zdj，其中j=1，2，…，2n。

2 线路参数计算方法

智能电表的测量数据均为标量，不包含相位信息。且负荷与线路均不是纯电阻元件，要尽可能准确地计算线路参数，就必须求取在同一参考相位下拓扑中所有电气量的相位角。且未安装测量元件的中间节点数量众多，利用总表及负荷处测得的标量信息来计算线路参数的难度很大。本文在拓扑已知的条件下，针对该问题提出了具有工程应用价值的计算方法。要指出的是，目前各个电表之间依然存在数据不同步的问题，对于数据的处理方法需要进一步研究。为了说明算法，本文暂不考虑数据同步性带来的计算问题。

以图1中的第一条大分支（分支负荷1~n）为例进行推导说明，第二条大分支的推导过程相似。对于其他辐射状低压配电网拓扑结构，推导原理同样适用。

2.1 功率倒推

（1）假定线路阻抗初值，求取每条负荷支路的功率损耗及每个负荷的功率因数角。

第j条负荷支路的功率损耗为

第j个负荷的复功率S j及功率因数角φj为

式中，j=1，2，…，n。

（2）计算各个中间节点的电压及各条线路的功率分布。

将最后一个负荷电压相量作为参考相量，对于末端两条负荷支路的公共节点Nn-1，如式（3）所示求取该节点电压值为

由于末端两条负荷支路连接在同一个中间节点，有：

式中：是负荷支路阻抗Zdn上方节点的电位。

根据式（5）求得流入该节点的功率、电流，以及该节点前方干线的功率分布为

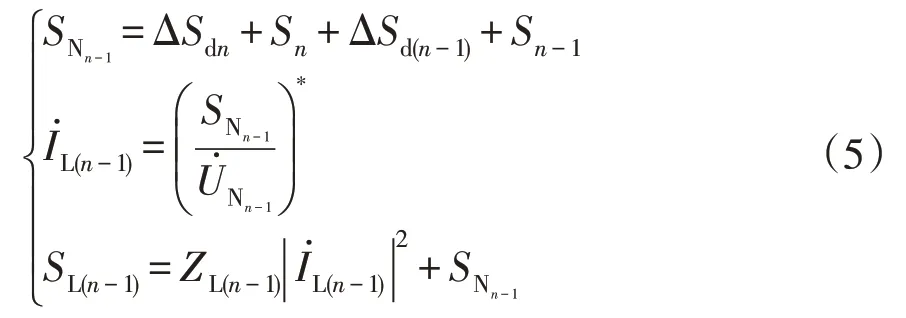
同理，对于其他中间节点Ni，可由式（6）求得该节点电压、流入该节点的电流、功率，及该节点前方干线的功率分布：

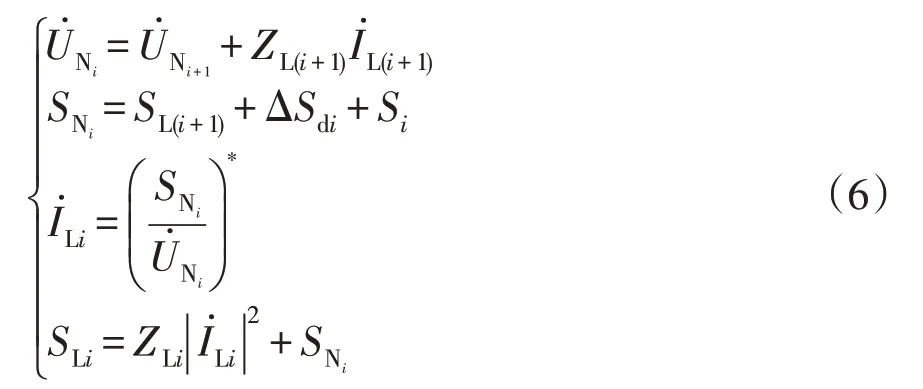
式中，i=n-2，n-1，…，1。

对于每个大分支，在此均要进行上述的功率倒推过程，从而得到整个拓扑的线路功率分布情况，以用于下一步计算。

2.2 电气量正推

（1）利用以上求得的线路功率分布，以电源电压相量为参考，由式（7）推得各二级干线电流相量及中间节点电压相量的新值为

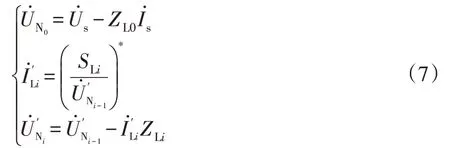
式中，i=1，2，3，…，n-1。

（2）求取以电源电压相量为参考的负荷电流相位角，并利用测量所得电压电流有效值及功率因数角，形成新的负荷电压电流相量。

由式（8）提取正推所得的负荷电流相量相位角为

将θi赋给测量得到的负荷电流有效值，组成新的负荷电流相量；并利用测得的功率因数角，同理形成新的负荷电压相量，即

式中，i=1，2，…，n。

利用相量与线路阻抗之间的相关性，在多个测量时刻下，计算所得电压电流幅值均与测量所得电压电流有效值相等时，计算所得电气量相位角便为实际相位角，进行计算所用的线路阻抗值便为实际阻抗值。

电气量相位角是由假定的线路阻抗初值推算而来的，而测量所得有效值隐含实际线路阻抗值信息。通过二者的结合及后续计算，可以达到利用测量所得有效值来逐步地修正线路阻抗初值的目的。

（3）根据配网拓扑结构及以上计算所得的电气量新值（带有右上撇），以线路阻抗新值（同样带有右上撇）为未知量，列写各个回路的KVL方程为

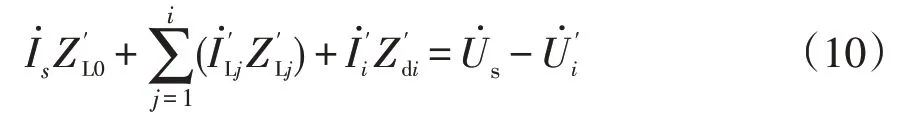
式中：i=1，2，…，n-1；为二级干线电流相量新值。

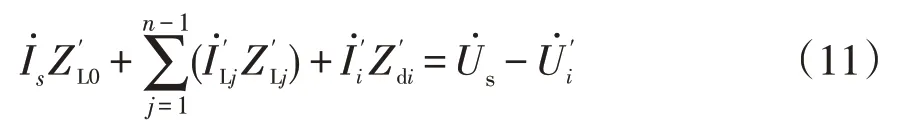
式中：i=n。

利用2.1节求得拓扑中所有线路的功率分布后，每个大分支均要进行上述的电气量正推，进而得到求取线路阻抗新值的KVL方程式。

2.3 方程组的求解

（1）利用最小二乘法求解由式（10）~（11）形成的超定方程组。对于式（10）~（11）中不同的i值所对应的不同表达式，可利用一个时间断面下的一组测量数据形成一个方程，多组测量数据便可形成关于该式的超定方程组，采用最小二乘法求解。虽然整个拓扑中的未知量个数较多，但可采用下述的递进求解法，使每次求解的未知量个数很少，计算速度快、准确度高。

当n≥3，对于i=1的式子，未知量为3个阻抗新值。求解

式中：上标（1），（2），…，（t）为不同的测量时刻。

将式（12）对应写为AZ′=B的形式。

式中：A为电流相量矩阵；B为电压相量矩阵；Z′即为待求阻抗矩阵。

求得阻抗值：、、。其中、为公共线路的阻抗值，可用于后续计算中。

然后求解i=2对应回路包含的各线路阻抗值：、、、。其中、已由i=1的式子求得，将、代入i=2对应的式子中，则未知量仅为两个新的阻抗值、，同理利用多个时刻下的测量数据进行对应超定方程组的求解，大大减少了每次求解的未知量个数。要指出的是，由于计算所用的电气量是由全局测量值推算而来的，该求解过程也是在全局测量值的约束条件下进行的。

以此类推，依次求解由i=1，2，…，k，…，n的式子形成的方程组，直至求解到末端负荷支路，便求解出一组线路阻抗新值。

（2）形成迭代计算过程并设定迭代终止条件。将求得的线路阻抗新值作为阻抗初值重新代入式（1）~（9）进行计算，并利用式（10）~（13）以及多组测量值重新求取线路阻抗新值，形成迭代过程。直至相邻两次迭代计算结果之差的二范数不超过设定范围后，输出线路阻抗计算结果。迭代终止条件如式（14）所示。

式中：Z′是计算所得的线路阻抗矩阵，下标（w）表示第w次的计算结果；E为收敛精度。

3 算法流程图

算法流程图如图2所示。图中判断框中的Z′与式（14）中的相对应，Z与式（14）中的相对应。

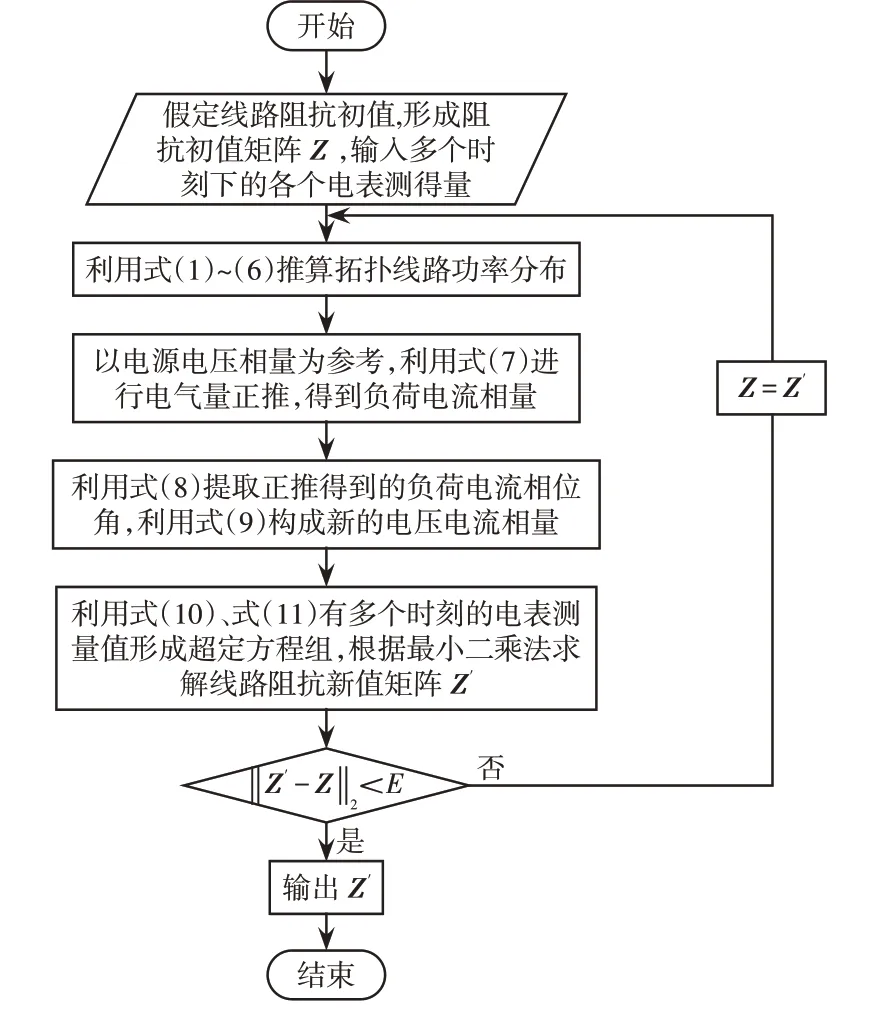
图2 算法流程Fig.2 Flow chart of algorithm

4 算法相关说明

设在一段测量时间内线路阻抗值不变，测量数组量及迭代的次数足够，则利用上述方法便可求解得到不断逼近线路阻抗真值的计算结果。在迭代过程中求得的阻抗新值是在测量所得的电压电流有效值及功率因数角的约束下，向真实阻抗值逼近的解。

1）参与计算的测量数据组需求量

目前智能电表能够以15 min为间隔上传测量信息，且低压配电网的负荷波动频繁，获取的数据组线性相关性不强。通过延长测量时间跨度便可获得足够的测量数组量以参与计算。

2）迭代次数及计算时间

需要求解的未知量个数及式子个数随拓扑的扩大而增多，但各个式子分别要求解的未知量个数不会大幅增加，每个方程组所要求解的未知量个数较少，计算量小。且求解的是线性方程组，计算速度很快，整体的求解时间较短。迭代次数与所采用的负荷数据及初始阻抗值的选取均有关，但无需纠结其中的定量关系。如果迭代结果收敛，且不随数据组的增多而产生大幅变化，则所用的数据及初始线路阻抗值便是满足要求的。

5 仿真验证

算例简化拓扑如图3所示，利用PSCAD及Mat⁃lab对算例进行仿真并计算其拓扑的线路阻抗，对比计算结果与PSCAD中实际设置的线路阻抗值。

图3 算例简化拓扑Fig.3 Simplified topology of example

图3 中，圆圈代表各个智能电表测量点。其中ZL0左侧圆圈代表电源出口处的总表测量点，其他带数字标号的圆圈代表负荷处电表测量点。该算例拓扑含有24个负荷电表节点，（若计入电源处电表节点及未安装测量元件的中间节点，共32个节点），31条支路。

即已知量为总表及24个负荷电表测得的有功无功功率、电压电流有效值，待求量为31条线路的阻抗值。

各条干线阻抗名称ZLi均已在图3中标示，PSCAD仿真中设置的干线阻抗值ZLi均为（0.050+j 0.015）Ω，其中i=0，1，…，6。数字1~24代表负荷电表编号，负荷电表所在线路为负荷支路，其阻抗名称为Zdj，仿真中设置的负荷支路阻抗值Zdj均为（0.010+j0.003 1）Ω，其中j=1，…，24；为简明，只在图3中标示了其中的Zd1及Zd24。

在线路长度未知的情况下，没有初值选取的参考依据，且随意设置的线路参数不具有代表性，因此目前在计算程序中设定初始线路阻抗值均为零。

当采用30组测量数据，收敛精度设置为10-10，测量数据没有附加误差时，线路阻抗计算结果如表1所示。由于PSCAD中只设置了两种线路阻抗值，且无测量误差时计算结果精确，表1中只简要表示出这两种阻抗值的计算结果。

表1 线路阻抗计算结果Tab.1 Calculated result of line impedance

由表1可以看出，当测量数据没有附加误差时，线路阻抗计算值与仿真设置值完全相等，这体现了方法本身的准确度及有效性。

为了在一定程度上模拟实际测量数据，仿真中给各个时刻下的电压电流有效值量测附加较小误差，误差标准差为3%。当采用30组测量数据，收敛精度设置为10-10时，所需迭代次数及计算时间如表2所示。

表2 迭代次数及计算时间Tab.2 Number of iterations and calculation time

从表2中可以看出，虽然所需迭代次数较多，但总的计算时间很短，这是因为求解的均为线性方程组，算法本身求解速度较快。与文献[17]所采用的二次规划优化算法相比，大大节省了求解时间。

附加测量误差时，计算结果如表3所示。

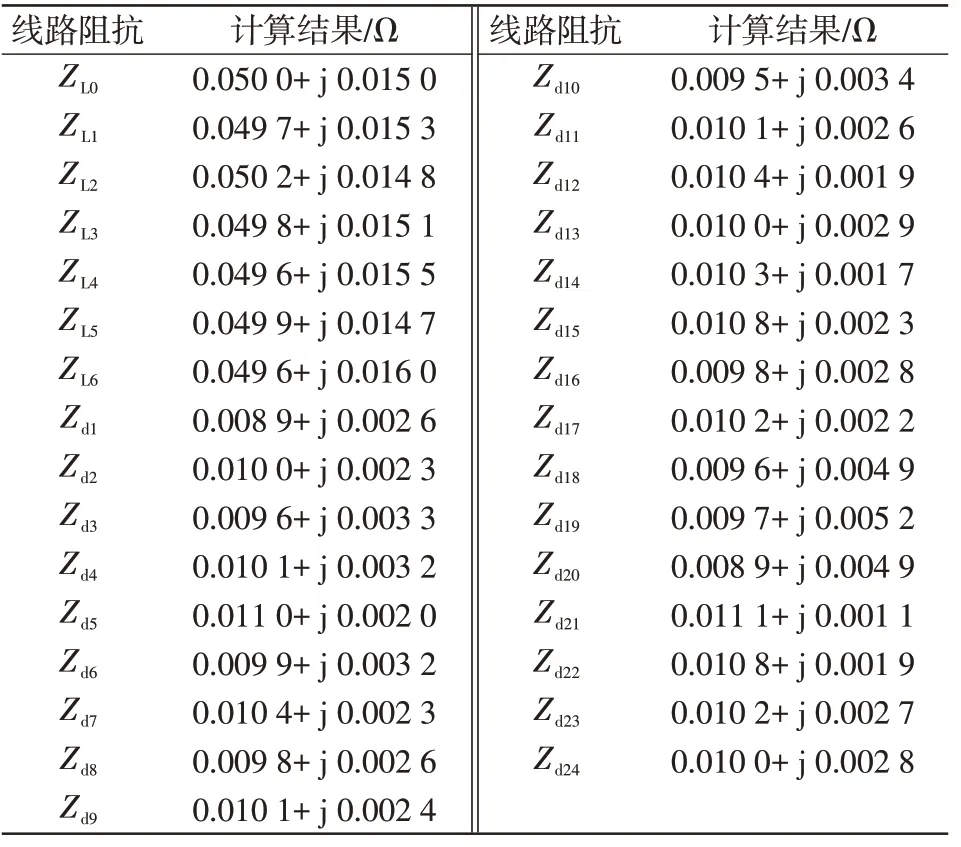
表3 附加测量误差时的线路阻抗计算值Tab.3 Calculated value of line impedance with additional measurement error

从表3中可以看出，在给测量数据附加误差的情况下，计算结果会产生误差，但在线路老化时，老化线路的电阻值增幅较大，产生的误差并不会掩盖线路阻抗增大的现象。将仿真模型中6条线路的电阻值增大，以模拟老化故障的发生。同样采用30组测量数据，附加误差标准差为3%的测量误差，收敛精度设置为10-10，老化线路阻抗的设置值及计算结果如表4所示。

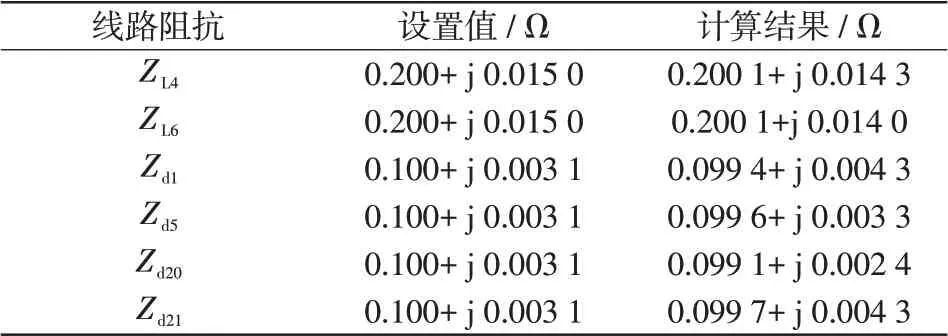
表4 老化线路阻抗值Tab.4 Impedance of aging lines

此时所需的计算时间为8.8 s，计算速度依然很快。

由以上分析可以推想，利用一个时间段内的测量数组可计算出当下的线路阻抗值，当线路阻抗发生变化时，由不同时间段内的测量数据组计算出的线路阻抗值也会相应发生变化。当某条线路阻抗增幅较大时，可依据计算所得的线路参数发出预警并及时定位该高危线路，节省检修时间及检修成本。

6 结语

智能电表提供了大量带有时标的测量数据，使一直以来较为薄弱的低压配电网相关研究得以深入进行，对提高电网精细化管理程度、降低运营成本、提高供电可靠性意义重大。

为验证算法的有效性，本文暂不考虑数据不同步带来的问题。但要说明的是，无论用何种方法，数据同步性及测量精度都是影响计算结果的重要因素，这就给量测体系提出了更高的同步性及精度要求，且未来需要研究更高级的数据处理方法来弥补测量数据的缺失及错误。

由于低压配电网线路分布不对称、负荷不对称，中性线上的电流难以确定，现有文献均未对中性线提出合理的处理方法。未来将面对三相四线制的不平衡低压配电网，研究中性线上的功率分布情况，以确定所有线路的功率分布，进而基于本文所提出的算法进行线路参数的求取。对于更加精确的三相四线制低压配电网线路参数求取来说，可能需要更完备的测量信息种类及更多测量点。