一种基于多通道卷积神经网络的小齿轮轴裂纹诊断方法

杜红梅，景亮亮，王后闯，杨阳，李凤林，樊懿葳

一种基于多通道卷积神经网络的小齿轮轴裂纹诊断方法

杜红梅1，景亮亮1，王后闯2，杨阳1，李凤林1，樊懿葳1

（1.成都运达科技股份有限公司，四川 成都 611700；2.北京纵横机电科技有限公司，北京 100081）

分析现有轨道车辆小齿轮轴故障诊断的技术特点，提出一种基于多通道卷积神经网络的小齿轮轴裂纹诊断方法。对轨道车辆电机输出端附近的振动加速度信号进行短时傅里叶变换，得到二维时频复数矩阵。将二维时频复数矩阵拆解成多通道后，压缩到统一大小，输入到CNN中训练获得诊断模型。通过小齿轮轴实测信号验证了本文方法的有效性与泛化能力，诊断精度高达98%，优于单通道二维时频矩阵变换后输入到CNN模型。该方法为小齿轮轴裂纹故障诊断提供了新途径。

小齿轮轴故障诊断；卷积神经网络；短时傅里叶变换；多通道

随着我国高速、重载铁路和城市轨道交通的快速发展，运营速度与载重随之增加，对轨道交通车辆运营和维护也提出了新挑战[1]。小齿轮轴作为轨道车辆走行部的关键部件之一，在长期高速重载的运行工况下由于设计或加工问题，极易在应力集中的区域出现裂纹甚至断裂的现象，直接影响轨道车辆的稳定性和安全性[2-3]。小齿轮轴处于走行部结构深处，常规的超声方法需对走行部齿轮箱进行拆解，才能让探头接触小齿轮轴端面实现探测。因此突破现有高速轨道车辆关键部件故障诊断技术壁垒、实现小齿轮轴裂纹故障非拆卸式有效诊断，是保障高速轨道车辆安全高效运行的重要途径。

基于信号处理与数据驱动的故障诊断方法是现有故障诊断方法的研究重点。其中基于信号处理的诊断方法主要通过对信号进行降噪、重构、解卷积等方法突出故障冲击特征，再寻找故障特征频率[4-6]。常用的信号处理方法有经验模态分解（Empirical Mode Decomposition，EMD）、短时傅里叶变换（Short Time Fourier Transform，STFT）和小波变换（Wavelet Transform，WT）等。陈丙炎等[7]采用振动信号的平方包络的自相关谱自适应地识别故障脉冲周期增强周期性脉冲特征，再进行解卷积增强原始信号中的故障频率，实现了轴承微弱故障诊断。钱林等[8]利用变分模态分解（Variational Mode Decomposition，VMD）获取振动信号的模态信号，利用互信息将其重构，最后利用形态学滤波进行降噪从而获得高信噪比信号，突出故障特征频率。该类方法存在计算效率快、硬件需求低、可解释性强的优势，但对于部分故障理论研究未涉及到的故障，获取相应故障特征频率很困难，因此也无法有效诊断故障[9]。

随着机器学习与深度学习的快速发展，将该类人工智能技术引入故障诊断领域已成为趋势[10]。Yuan等[11]利用局部平均分解获取振动信号的特征向量，再基于该特征向量建立支持向量数据描述（Support Vector Data Description，SVDD）故障诊断模型。Gopi等[12]利用长短时记忆网络（Long Short-Term Memory，LSTM）对发动机故障进行特征提取与故障诊断，在复杂工况、混合故障以及强噪声的环境下取得了较好的效果。冯泽阳等[13]利用小波变换获取能量特征向量，结合振动信号的时域特征，使用支持向量机（Support Vector Machine，SVM）完成列车转向架的故障诊断。王立平等[14]利用小波包分解对原始信号进行分解，再利用局域判别基进行信号能量重构，最后将归一化的特征向量输入梯度提升树（Gradient Boosting Decision Tree，GBDT）进行预测，相比于传统方法具有更高的诊断精度与更强的鲁棒性。

通过以上常规机器学习，诊断算法虽已取得丰硕成果，但对仅存在微弱振动故障特征的小齿轮轴裂纹故障，在强噪声运行环境下，数据特征并不明显，其诊断精度并不高。而基于卷积神经网络（Convolutional Neural Networks，CNN）的深度学习模型通过对振动加速度数据的迭代优化，能挖掘数据潜在故障特征。朱会杰等[15]提出权值求和与最大尺度最大值池化策略，有效解决了特征的平移不变性与小样本泛化能力弱的问题。邓佳林等[16]增加特征通道权重模块来获取通道的全局信息，并通过通道间的依赖关系进行权重调整，增强模型的特征提取能力，实验表明该方法相比传统方法诊断精度提高了20%左右。Han等[17]利用CNN对轴承振动的时域数据进行特征提取，然后将CNN提取的特征输入到支持向量机进行轴承状态识别，具有耗时少、精度高、泛化能力强等特点。李恒等[18]利用短时傅里叶变换将一维振动信号转化为二维频率信号，随后输入到分类器实现了轴承故障诊断。Chen等[19]利用小波变换将振动信号转换为包含时频信息的二维信号，然后将其输入到CNN模型进行故障诊断。Wu等[20]使用1-DCNN模型对固定轴齿轮箱和行星齿轮箱的故障诊断问题进行研究，证明了其有较强的特征提取能力和分类能力。但上述方法均使用单通道信号输入CNN进行故障诊断，无法充分发挥CNN提取并增强振动信号特征的能力，无法充分挖掘故障特征。

基于上述分析，本文提出一种基于多通道卷积神经网络、应用于小齿轮轴裂纹故障振动信号的特征提取，从而显著提升分类器的故障诊断能力。本文的主要贡献点为：①采用短时傅里叶变换对振动信号进行有效分解，并将得到的频谱信息转化为CNN的多通道输入，有效地将一维振动信号转化为CNN更为擅长的多通道矩阵识别问题；②多通道二维时频矩阵比单通道二维时频矩阵信号表达特征更加全面，CNN可以充分提取信号中的隐含特征。

1 基于短时傅里叶变换的CNN模型

1.1 短时傅里叶变换

傅里叶变换可以将复杂的原始振动信号从时域变换为较为简单的频率信号，是平稳信号分析常用方法，但对于非平稳故障信号，傅里叶变换的全局性频域表征是致命的，它无法表征信号在时间维度上的局部故障特征。在缺少时间维度的局部信息时，故障的精细化诊断往往会出现一定程度的误差。因此在故障诊断的过程中需要对信号进行时频域的综合分析，短时傅里叶变换也随之出现。其基本思想是将一段非平稳随机信号看作是一小段平稳随机信号的叠加，即让特定大小的窗口在时间维度上按固定步长滑动，计算每一个窗口中振动信号的傅里叶变换，再将每一个窗口中的频域信号进行拼接，获取信号的时频矩阵，该矩阵表示了信号频率随时间的变化趋势[21]：

式中：(,)为时频矩阵；为时间；为频率；(′)为均值化后的振动加速度数据；(－′)为短时傅里叶变换窗函数；′为窗函数的中心位置；-jωt′为复平面上关于频率的基函数。

1.2 CNN

常规机器学习故障诊断算法往往由浅层结构构成，这导致了该类算法需要人为预先处理数据提取故障特征。为了获取良好的预测效果，需要投入大量的人力物力研究故障机理、模型特性等。并且在面临新的故障对象时需要从头开始研究故障并构造相关特征，可扩展性差。而深度学习通过构造信号的非线性映射，达到自动提取信号特征的目的。网络结构中的每一层都具有特征变换与提取的能力，通过逐层的特征变换将信号由复杂的结构映射为多个稀疏的特征表达，无需人工干预即可进行故障高精度预测。由于对轨道车辆小齿轮轴裂纹故障机理研究较少，无法获知其故障频率，短时傅里叶变换后无法利用传统的信号处理方法突出其故障频率特征。因此需要引入深度学习中的CNN自动提取时频矩阵中的故障特征。

CNN模型的隐藏层包含了卷积层、池化层、全连接层。原始数据经过多次的卷积层与池化层将特征抽象化，最后采用全连接层整合这些特征输出预测结果。

卷积层主要由多个卷积核构成，卷积核具有局部连接与权值共享的特性。由卷积核在时频矩阵中滑动，将每个窗口中的数据变换为稀疏的特征，卷积核决定局部窗口什么特征该被激活、什么特征该被抑制。一个卷积核仅能提取一个维度的特征信息，而一个图像矩阵往往存在数十上百个特征，因此卷积核的个数需尽可能多，利用权值共享技术在增加卷积核的过程中降低模型的复杂度。卷积的具体过程为：

当前层数；、为当前层矩阵坐标；为被卷积核覆盖的矩阵；、为卷积核覆盖矩阵的长和宽；为核函数；为对应偏置项。

对卷积后的特征非线性化，可以较好地拟合各类故障不同的分布特征。常用的非线性化激活函数为ReLu，具体表现形式为：

()＝max(0,) （3）

在整个模型中全部应用卷积层会导致参数过于庞大，模型也更容易出现过拟合的现象。利用池化层可以将矩阵数据进一步降维，优化参数数量，减少计算量；同时池化层可以增强矩阵特征的平移、旋转不变性，增强模型的泛化能力。上采样池化具体表现形式为：

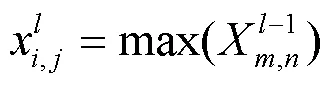
矩阵经过多次卷积层与池化层已提取出较有代表性的特征，需要变为可判别的特征向量，因此利用平铺层将特征变为一维特征向量，同时弱化特征的空间特性。再利用全连接层将特征降维整合，获取最终的故障特征并加以判别。全连接层层数越深或神经元越多，越能提高故障特征的预测能力，但很容易过拟合，因此需要控制全连接层参数。全连接层公式为：

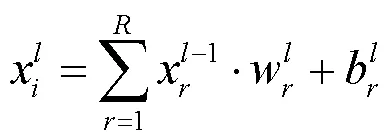
接层当前层数；为一维矩阵索引值；为－1层特征向量长度；为权重矩阵；为偏置项。

全连接层中同样需要激活函数将其非线性化，选用softmax函数，其广泛应用于二分类模型以及多分类模型中，表达形式为：

索引；为对应类别索引值；所有类别索引值。

1.3 基于多通道卷积神经网络

为有效识别小齿轮轴裂纹故障，本文基于多通道时频矩阵搭建的CNN结构如图1所示。可知，本文的多通道时频矩阵CNN模型首先由4层卷积层与池化层构成，其中前2层卷积层与池化层用于提取时频矩阵的浅层特征，后2层卷积层与池化层将浅层特征抽象化为更强表征能力的高层特征。利用平铺层将输出变为一维特征向量，由2层全连接层进一步提取特征，并预测故障诊断结果。为了增强模型的非线性化预测能力，卷积层采用ReLu激活，全连接层采用softmax激活。针对模型易过拟合的问题，在所有层中均采用0.2比例的dropout。

图1 多通道时频矩阵CNN结构

2 数据验证与讨论

为了验证本文提出方法的有效性，分别对小齿轮轴裂纹故障数据构建单通道数据和多通道数据，进行故障诊断，采用国内某机务段出现部分小齿轮轴裂纹故障数据进行实验验证。

2.1 实测数据处理及诊断流程

本文所用数据采自国内某机务段HXD1C车型标配走行部故障检测系统，数据集包含出现小齿轮轴裂纹故障轴位的数据。数据采集的传感器安装位点为走行部电机的输出端，传感器的位置如图2所示，采样频率为40 kHz，图3为一条小齿轮故障的局部原始时域信号。轨道车辆每回库一次，即下载该运行里程的振动加速度数据，最终采集1轨道车辆在不同时间段下28个交路电机输出端振动加速度数据。

基于二维CNN的小齿轮轴裂纹故障诊断流程如图4所示：对振动信号按照每0.25 s进行数据分割；根据确定的STFT的参数进行STFT变换，分别得到单通道二维时频图与多通道二维时频图；将得到的时频图输入至二维CNN中进行模式识别，根据正确率等因素优化CNN参数、确定模型。

图2 HXD1C车型小齿轮轴承传感器

图3 一条小齿轮故障原始时域信号

图4 CNN模型的诊断流程图

2.2 数据验证结果

为了展示本方法的优越性，设置了一组对比实验：将原始小齿轮轴裂纹故障时域信号进行过短时傅里叶变换后，生成的单通道二维（101×101×1）时频矩阵输入到经典CNN模型中；生成的多通道二维（101×101×2）时频矩阵输入到经典CNN模型进行故障分类。模型结构如表1所示，其中四个卷积层的滤波器数分别为32、64、128、256，卷积核大小为3×3。

表1 STFT参数取值

表2 CNN网络结构参数

使用一列存在小齿轮轴裂纹故障的机车数据进行训练，迭代次数为40。本文提出的方法与对比方法的实验结果如图5所示。可知，训练集中，单、多通道的准确率均已超过95%，且多通道稍优于单通道；测试集中，多通道准确率已超过98%，而单通道准确率鲜有到达95%。证明多通道二维时频矩阵在故障诊断中效果优于单通道二维时频矩阵。

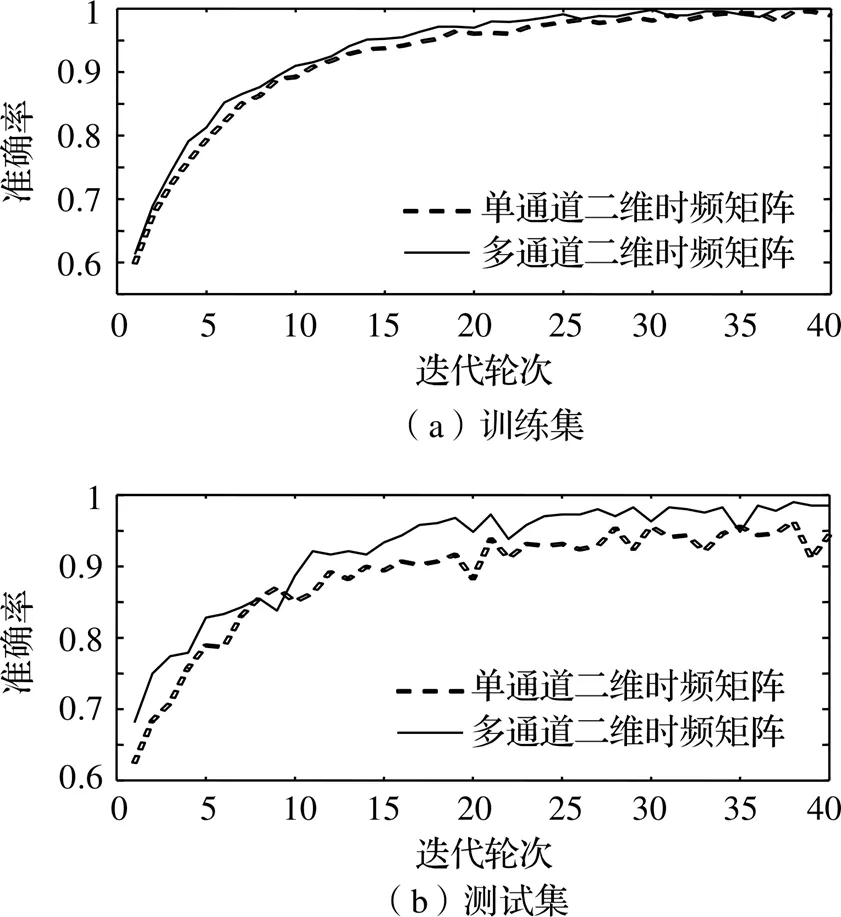
图5 训练集和测试集的故障识别准确率对比

3 结语

利用短时傅里叶变换直接对原始小齿轮轴振动信号进行自动提取特征，得到二维时频矩阵，将转换后的多通道二维时频矩阵输入到CNN模型中，在小齿轮轴裂纹故障诊断中取得了较好的效果，可以得到如下结论：

（1）原始小齿轮轴振动信号经过STFT后得到的时频矩阵，可以保留原始信号的时域信息和频域信息，经过转换得到的多通道二维时频矩阵特征信息优于单通道二维时频矩阵，能够突出反映小齿轮轴故障状态信息。

（2）基于二维CNN的小齿轮轴裂纹故障诊断方法具有一定的诊断优越性，实现了小齿轮轴裂纹故障端到端的自适应诊断，对之后小齿轮轴裂纹在线诊断算法研究具有启发意义。

本文模型虽然实现了小齿轮轴裂纹的端到端在线诊断，但由于机车运行环境的复杂性，仍存在一定的优化空间：①增加牵引、制动、转速等额外信息到模型中，可有效降低模型的误判率；②改进模型结构，使其在同样本下具有更强的特征提取能力；③增加迁移学习的思想到模型中，可将该模型的结果应用到其他运行线路、机车类型，不受环境因素制约。

[1]沙美妤，刘利国. 基于振动信号的轴承故障诊断技术综述[J]. 轴承，2015（9）：59-63.

[2]彭志亮，左华付，肖先忠. 机车电机转轴及小齿轮轴断裂失效分析[J]. 机械工程材料，2011，35（6）：93-97.

[3]朱有利，王燕礼，唐亮，等. HXD1机车小齿轮轴断裂失效应力分析[J]. 材料科学与工艺，2017，25（1）：69-75.

[4]McDonald，Geoff L，Qing Z. Multipoint Optimal Minimum Entropy Deconvolution and Convolution Fix: Application to vibration fault detection[J]. Mechanical Systems and Signal Processing，2017（82）：461-477.

[5]Wang X，Liu C，Bi F，et al. Fault diagnosis of diesel engine based on adaptive wavelet packets and EEMD-fractal dimension[J]. Mechanical Systems and Signal Processing，2013（41）：1-2.

[6]Mohanty S，Gupta K，Raju K. Comparative study between VMD and EMD in bearing fault diagnosis[C]. IEEE International Conference on Industrial and Information Systems. IEEE，2014.

[7]陈丙炎，宋冬利，张卫华，等. 改进MOMEDA方法及其在滚动轴承故障特征增强中的应用[J]. 机械强度，2021，43（1）：1-8.

[8]钱林，康敏，傅秀清，等. 基于VMD的自适应形态学在轴承故障诊断中的应用[J]. 振动与冲击，2017，36（3）：227-233.

[9]Kankar P，Sharma Satish C，Harsha S. Fault diagnosis of ball bearings using machine learning methods[J]. Expert Systems With Applications，2010，38（3）：1876-1886.

[10]Wang R，Meng X，Xiong B，et al. Multi-view Bearing Fault Diagnosis Method Based on Deep Learning[J]. Journal of Physics：Conference Series，2021，1757（1）：012093.

[11]Yuan Z，Song F，Dou R. Research on Bearing Fault Diagnosis of Submersible Pump Motor Based on LMD and SVDD[J]. IOP Conference Series：Materials Science and Engineering，2020，711（1）：012041.

[12]Gopi K，Selvaraj B，Mittal M，et al. Swarm-LSTM：Condition Monitoring of Gearbox Fault Diagnosis Based on Hybrid LSTM Deep Neural Network Optimized by Swarm Intelligence Algorithms[J]. Computers，Materials and Continua，2020，66（2）：2041-2058.

[13]冯泽阳，邬平波. 基于SVM的转向架故障诊断技术研究[J]. 机械，2020（8）：37-43.

[14]王立平，邓芳明. 基于小波包和GBDT的瓦斯传感器故障诊断[J]. 测控技术，2016，35（12）：30-33.

[15]朱会杰，王新晴，芮挺，等. 基于平移不变CNN的机械故障诊断研究[J]. 振动与冲击，2019，38（5）：45-52.

[16]邓佳林，邹益胜，张笑璐，等. 一种改进CNN在轴承故障诊断中的应用[J]. 现代制造工程，2020（4）：142-147.

[17]Han T，Zhang L，Yin Z，et al. Rolling bearing fault diagnosis with combined convolutional neural networks and support vector machine[J]. Measurement，2021，177（1）：109022.

[18]李恒，张氢，秦先荣，等. 基于短时傅里叶变换和卷积神经网络的轴承故障诊断方法[J]. 振动与冲击，2018，37（19）：124-131.

[19]Chen R，Huang X，Yang L，et al. Intelligent fault diagnosis method of planetary gearboxes based on convolution neural network and discrete wavelet transform[J]. Computers in Industry，2019（106）：48-59.

[20]Wu C，Jiang P，Ding C，et al. Intelligent fault diagnosis of rotating machinery based on one-dimensional convolution neural network[J]. Computers in Industry，2019（108）：53-61.

[21]王程，郑小燕，王海彬. 基于短时傅里叶变换的干扰信号识别方法[J]. 装备环境工程，2018，15（3）：67-70.

A Method for Pinion Shaft Crack Diagnosis Based on Multi-Channel Convolutional Neural Network

DU Hongmei1，JING Liangliang1，WANG Houchuang2，YANG Yang1，LI Fenglin1，FAN Yiwei1

( 1.Chengdu Yunda Technology Co., Ltd., Chengdu611700,China; 2.Beijing Zongheng Electro-Mechanical Technology Development Co., Ltd.,Beijing100081,China )

Based on the analysis of the existing technical characteristics of pinion shaft fault diagnosis for rail vehicles, this paper proposed a method of pinion shaft crack diagnosis based on multi-channel convolutional neural network (CNN). Short-time Fourier transform is performed on the vibration acceleration signal near the output terminal of the rail vehicle motor to obtain a time-frequency complex matrix, and two-dimensional time-frequency complex matrix was disassembled into multiple channels, compressed to a uniform size and put into CNN to train to obtain a diagnostic model. The effectiveness and generalization ability of the method are verified by the measured signals of the pinion shaft. The diagnosis accuracy is as high as 98%, which is superior to the single channel two-dimensional time-frequency matrix transformation and input into CNN model. The proposed method provides a new approach for the pinion shaft crack diagnosis.

pinion fault diagnosis；convolutional neural network；short time Fourier transform；multi-channel

TH133.33

A

10.3969/j.issn.1006-0316.2022.07.006

1006-0316 (2022) 07-0036-06

2021-12-02

杜红梅（1985－），女，山东泰安人，硕士，工程师，主要研究方向为车辆转向架旋转部件故障智能检测、健康评估及智能运维，E-mail：903499926@qq.com；景亮亮（1991－），男，山东济南人，硕士，工程师，主要研究方向为机器学习与故障诊断技术。