基于非凸复合函数的稀疏信号恢复算法
周洁容 李海洋 凌 军 陈 浩 彭济根
根据奈奎斯特(Nyquist)采样定律,想要实现信号的无失真输出,采样频率必须在信号带宽的两倍以上.然而,在大多数情形下,按此定律采样所获得的信息是冗余的,这不仅造成采样的浪费,而且处理较大带宽的信号时会给硬件系统带来巨大压力.压缩感知(Compressed sensing,CS)[1]的出现使该问题的解决成为可能.压缩感知是一种新型的信号采样及重构理论,利用少量的测量值就可以实现稀疏或可压缩信号的精确重构.而稀疏信号的重构在众多科学研究和工程应用中十分重要,如物理学中的量子态层析成像[2]、天体物理学成像[3]、磁共振成像[4]、信号处理[5]、雷达成像[6]等,CS 理论的引入加快了上述应用的研究和发展.
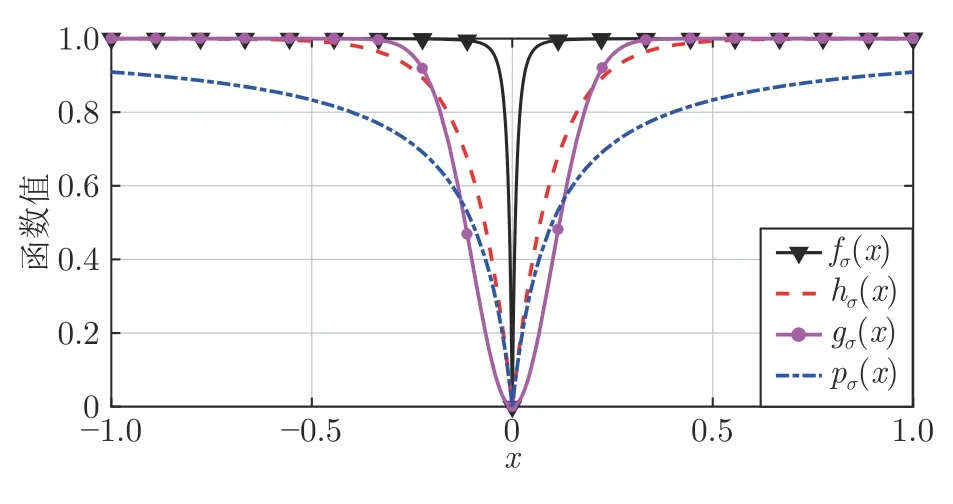
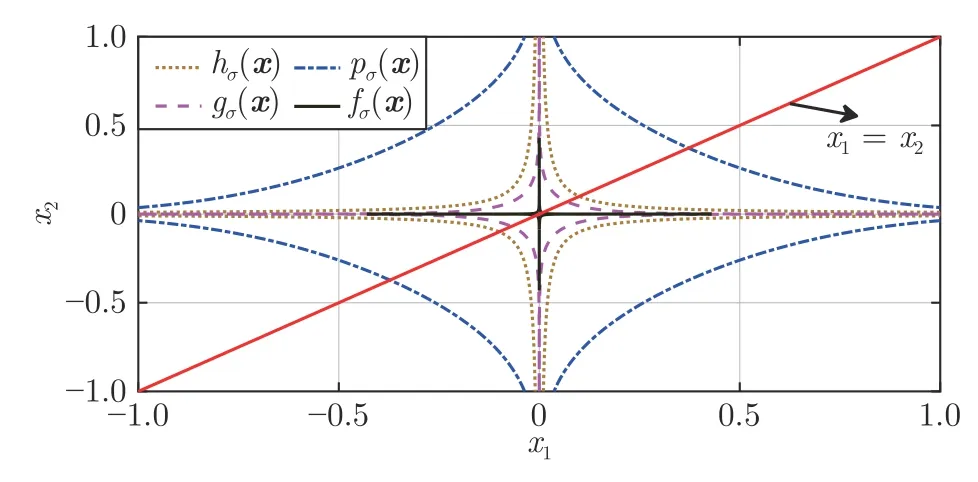
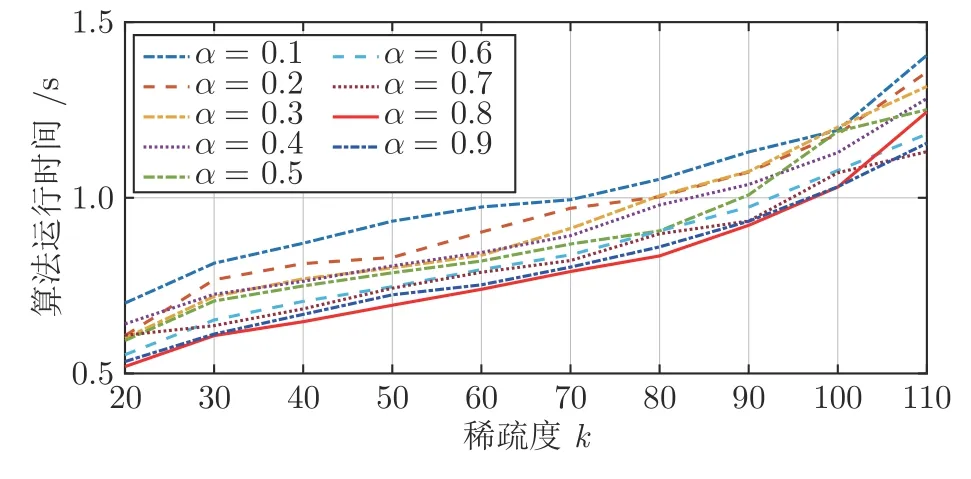
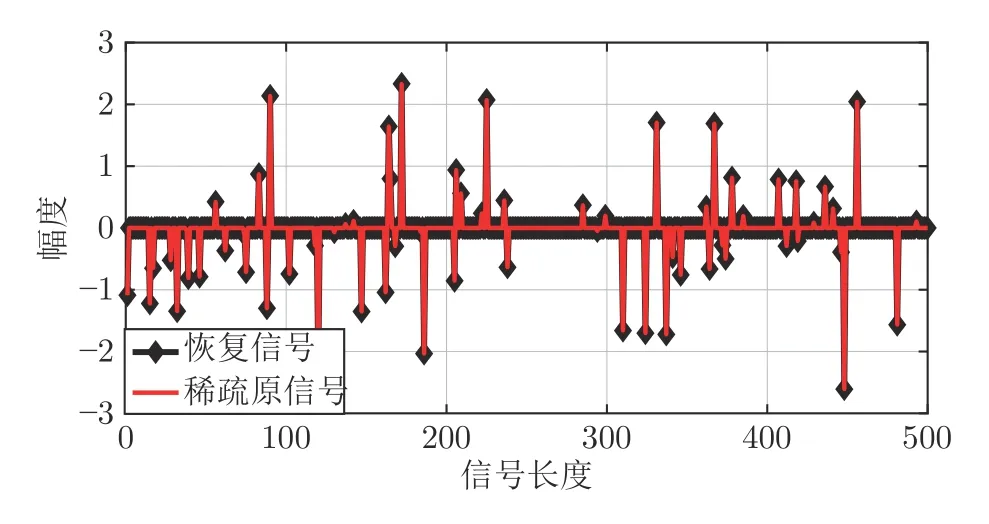
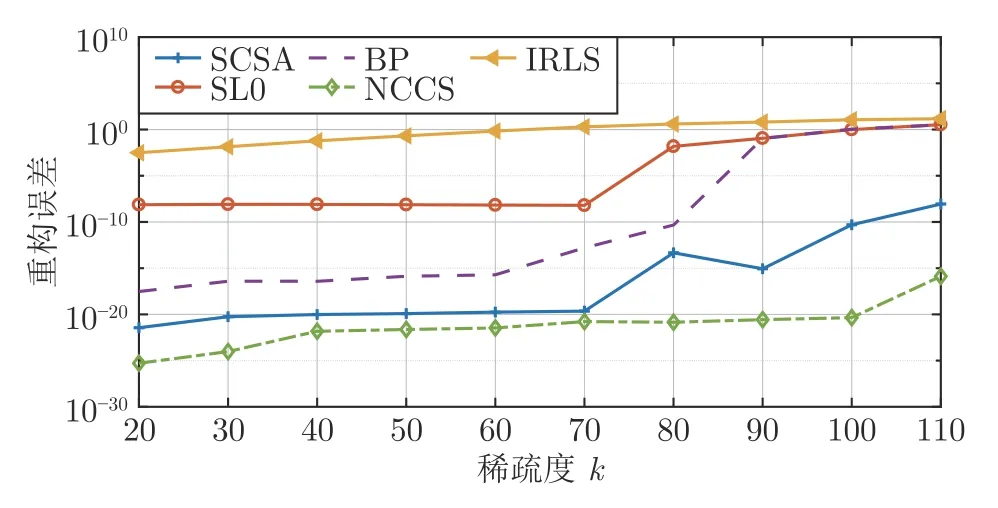
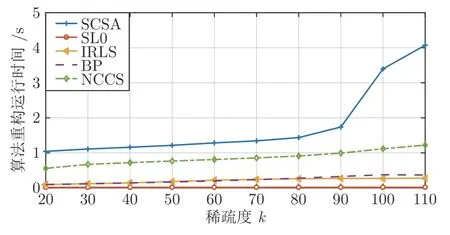
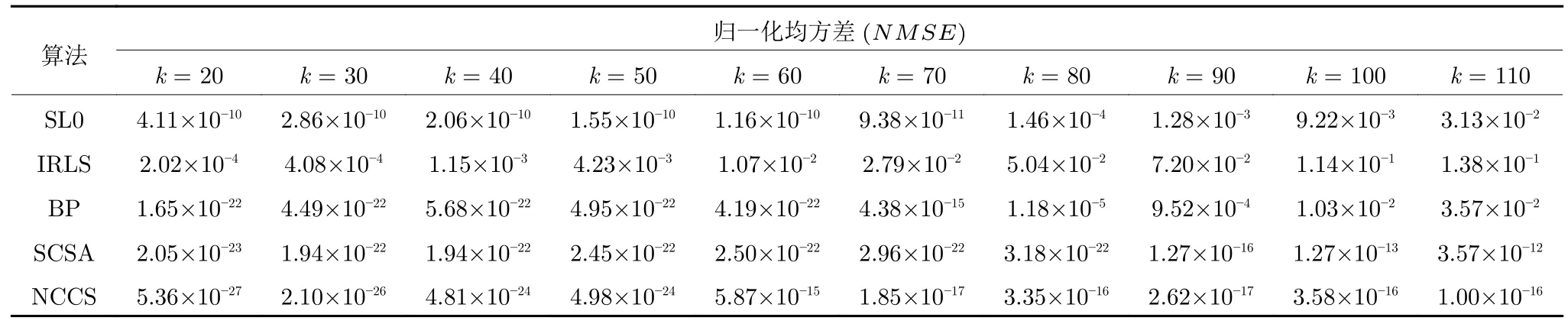
数学上,稀疏信号重构是指从欠定线性系统bAx中恢复原始信号x,其中b∈Rn是测量向量,A∈Rn×m(n 其中,‖x‖0表示向量x中非零元素的个数[7]. 已经证明,(P0)模型的直接求解是NP(Nondeterministic polynomial)难的[8],其计算量会随着稀疏向量维数的增加而增大,模型的抗噪能力也很差.为此人们提出了多种方法对 (P0) 模型进行求解,主要方法可归类于启发式方法、凸松弛方法、非凸松弛方法三种类型.典型的启发式算法有正交匹配追踪[9]、阈值算法[10]、子空间追踪算法[11]、分级正交匹配追踪[12]等,这些算法重构理论简单、速度较快,但往往需要更多观测,算法的重构精度较低、收敛速度较慢,并且在有噪声情况下信号的恢复精度较低,因此其应用范围有限.典型的凸松弛算法有梯度投影算法[13]、BP (Basis pursuit)算法[14]、BPDN(Basis pursuit denoising)算法[15]、IRLS (Iterative reweighed least squares)算法[16]、Bregma 迭代法[17]等,其中最经典的是BP 算法,文献[18]证明了在测量矩阵满足有限等距性质[19]的条件下BP 模型与(P0)模型等价,但在多种情形下BP 模型中的L1范数不能充分反映信号的稀疏性特征,往往难以获得稀疏解.为此,人们提出了用非凸泛函替代L0范数的方法,称之为非凸松弛方法. 相较于L1范数,许多非凸泛函能更好地近似L0范数,从而更好地反映信号的稀疏性特征.典型的非凸松弛算法有NSL0 (Newt-on smoothL0norm)算法[20]、SL0 (SmoothedL0)算法[21]、CTNRAL0 (Composite trigono-metric function nullspace reweighted appro-ximateL0norm)算法[22]、SCSA (Successive concave sparsity approximation)算法[23]等.易见,松弛方法的核心是寻找L0范数的逼近函数,通过极小化该逼近函数寻得最稀疏解.显然这种近似模型对 (P0) 模型的逼近性能取决于所选取的近似函数对L0范数的逼近程度.因此,如何构造具有更优逼近性能的近似函数已成为稀疏信号重构问题研究中的重要问题. 最近,文献[23−24]分别构造了两种近似函数gσ(x)1−e−|x|/σ、hσ(x)|x|/(|x|+σ)以实现对L0范数的逼近,取得了较好的重构效果.一个有趣的想法是,如果将上述每个泛函对信号的作用看成是一次前向(Forward)处理过程,那么我们是否可以通过泛函的复合实现对信号的深度作用,从而提高信号重构的性能? 基于这种想法,本文将上述两个泛函进行复合,构建一种新的非凸松弛模型,给出该模型的理论分析,对该模型提出一种新的近似算法,并通过数值实验验证算法的有效性以及相较于SL0 算法、IRLS 算法、BP 算法、SCSA 算法等经典算法的优越性. 设δ为Kronecker 函数,即 这样,下面的优化问题可看成是 (P0) 问题的近似模型 文献[21,23−24]分别采用以下三种DA 函数来实现对L0范数的逼近 并通过对相应近似模型的求解实现了信号的精确重构. 显而易见,近似式(3)对 (P0) 模型的逼近性能取决于所选取的DA 函数对L0范数的逼近程度.因此,如何构造具有更优逼近性能的DA 函数已成为稀疏信号重构问题研究中的重要课题.注意到,上述DA 函数hσ(x) 和gσ(x)都能很好地实现对L0范数的逼近.一个自然的问题是,是否可以将这两个函数进行复合以实现对L0范数的深度逼近? 针对这个问题,本文对上述两个函数hσ(x) 和gσ(x) 的复合进行考察 其中,“◦”表示函数复合运算,显然这是一个DA 函数.不仅如此,可以从几何图像和理论分析上说明,在固定参数σ后该DA 函数相对于hσ(x)、gσ(x)、pσ(x)具有更好的对L0范数的逼近性能. 1)几何图像分析 图1 展示了pσ(x)、hσ(x)、gσ(x) 以及复合函数fσ(x)这4 种DA 函数的几何图像,其中参数σ0.1.可以看出,在x0附近,pσ(x) 函数曲线最平坦,而本文所提出的复合函数fσ(x) 的图像曲线相对其他三种函数最为陡峭,这表明函数fσ(x)具有对L0范数最好的逼近效果. 图1 4 种函数在 σ0.1 时的一元函数分布Fig.1 The unary distribution of the four functions at σ 0.1 图2 展示了pσ(x)、hσ(x)、gσ(x)和fσ(x) 4 种DA 函数在二维情形的等高几何图像,即pσ(x)hσ(x)gσ(x)fσ(x)1的图像,其中参数σ0.1.可以看出,在4 种函数与直线x1x2的交点中,函数fσ(x) 与x1x2所表示的直线得到的交点的分量绝对值最小,这表明复合指数函数fσ(x) 能更好地逼近L0范数. 图2 pσ(x)、hσ(x)、gσ(x)和函数 fσ(x)在 σ0.1 时的二元函数分布Fig.2 The bivariate distribution ofpσ(x),hσ(x),gσ(x)and the function fσ(x)atσ 0.1 2)理论分析 上述从几何直观上展示了复合指数函数相对于其他DA 函数的更好逼近性能.不仅如此,也可以从理论上证明,对区间 (0,0.9)内任意非零参数σ,复合指数函数相对于pσ(x)、hσ(x)、gσ(x) 都具有更好的逼近性能.不失一般性,仅在第一象限内进行讨论,即假定x ≥0.对区间内任意σ(0),因为 首先,固定函数值比较对应变量的大小. 假设hσ(x)gσ(x)r,其中 0 因为 所以有R(r)为增函数,即对任意r有R(r)>R(0)0,得xh >xg.这说明相较于hσ(x),函数gσ(x) 更贴近坐标轴. 下面固定变量x,比较函数值pσ(x)、gσ(x)、fσ(x)的大小.因为 所以,为讨论gσ(x)、pσ(x) 的大小关系,只需要比较指数的大小.易得x趋于 0(至少在x ≤2σ时),对任意非零σ恒有 即gσ(x)≥pσ(x). 同理,对 进行讨论,由于 所以,在x0附近(至少在|x|≤0.1 范围内)有fσ(x)≥gσ(x).因此有 说明fσ(x) 的函数曲线更陡峭. 利用函数的对称性,其他象限也可类似讨论.所以由上述函数的几何图像和理论分析也能得出fσ(x)相对于hσ(x)、gσ(x)、pσ(x) 具有更强的稀疏性. 以上分析表明,由式(7)定义的复合函数fσ(x)具有对L0范数更优的逼近性能.为此,考虑由该函数所诱导的优化模型 下面对优化模型 (CE) 与 (P0) 之间的关系进行研究,为此首先证明以下引理. 引理 1.设模型 (CE)的最优解为x∗,其稀疏度为k,则矩阵A中对应解x∗支撑集的子矩阵Ak是列满秩的,其中x∗的支撑集是指集合i1,···,m}. 证明.利用反证法,假设矩阵Ak不是列满秩的,即矩阵的列向量线性相关,则存在非零向量v,其支撑集包含在向量x∗的支撑集内,并且使得Akv0.显然,向量x∗±v满足约束条件Axb.不失一般性,假设向量v中最大的分量绝对值不超过向量x∗中最小的分量绝对值. 根据函数fσ(x) 的严格凹性,有 这表明Fσ(x∗+v) 上述引理1 表明,模型 (CE)的最优解x∗满足即模型的最优解包含在有限集Γ是列满秩矩阵}中. 定理1.对任意感知矩阵A和测量向量b,存在一个依赖于A和b的常数σ(A,b),当0<σ <σ(A,b)时,模型 (CE)与模型 (P0) 等价. 证明.要证明模型 (CE)与模型 (P0) 等价,则只需证明模型 (CE) 的最优解为模型(P0) 的最优解即可. 根据引理1,可以得到以下等价关系 说明对任意σ,(CE)模型的最优解x˜∈Γ,其中 Γ 为有限集. 下面证明存在一个常值σ(A,b),当0<σ <σ(A,b)时,存在唯一一个点∈Γ均是 (CE) 最小化模型的解,下面利用反证法进行求证. 为克服函数Fσ(x) 在原点不可微带来的不便,可以将稀疏优化模型 (CE) 转换为以下优化问题.令未知量xu −v,其中u,v∈Rm,u拥有x中所有正元,其余元素为零;v拥有x中所有负元的绝对值,其余元素也为零.用z[uT,vT]T∈R2m表示拼接向量.经过替换,易得 此时,约束条件Axb转换为[A,−A]zb.那么无噪模型 (CE) 转换为 为了便于求解式(14),利用文献[25]中介绍的MM优化方法. MM 优化方法指当目标函数较难实现优化时,通常可以选择更容易优化的替代目标函数,当替代函数满足一定的条件时,其最优解能够无限逼近原目标函数的最优解.通过利用凹函数Fσ(z)的一阶判别条件以及 MM 优化方法对目标函数Fσ(z) 进行放缩,可得 记 即 其次,因为 有 再利用假设式(20)有 由此可知,对任意ε2>0,存在K2>0,对任意k >K2,有 故结合式(23)、式(25)可知,对任意z ∈ℵ,对于式(22)可得 即对任意z ∈ℵ,有任意ε3>0,存在K3>0,对任意k >K3,有 令εmin(ε1,ε2,ε3),Kmax(K1,K2,K3),当k >K时,对不等式(29)有 由式(30)可知 对左端加减同一项,有 对式(31)移项,有 再对式(32)不等号左端进行放缩,得 最后结合式(32)、(33)得 优化模型(21)简记为 为给出模型(14)的有效求解算法,需要对算法初始值的选择进行分析,首先给出复合函数的如下性质. 其中,关于 e−|x|/σ(|x|+σ)/(|x|+σ)3、e−|x|/σ(|x|+σ)/(|x|+σ)4的任意阶导数满足有关 (|x|+σ)−1的次方数不低于 3次,则(n ≥2)关于参数σ−1的次方数不低于 3 次.由此可得 利用式(35)、(36),有 引理2 表明,在时,最小化Fσ(x) 近似于最小化‖x‖1. ‖x‖1的凸性使得算法陷入局部极值的可能性减少,从而提高算法重构精度.鉴于此,本文在设计算法时取初始值为以下问题 的解. 在此基础上,提出如下算法. 步骤1.输入:A,b,ε1,ε2,ε3. 步骤2.初始化: 步骤3.算法迭代: 步骤4.输出稀疏向量:x=xk. 其中,步骤 3 算法迭代环节由内、外两部分循环构成.外循环为步骤 a)~b) 以及 f)~h),循环利用参数σ实现复合函数对L0范数的逐次逼近.内循环即步骤c)~e),结合外点罚函数法[26]和共轭梯度法迭代求解模型(14),具体为利用外点罚函数法引入正则参数实现模型(14)的无约束转换,再通过共轭梯度法求解无约束优化问题.最后在步骤j)~k),针对共轭梯度法求得的非稀疏解,利用加权L1范数最小化[27]进行稀疏化处理.其中,d1和d2分别表示外循环和内循环连续迭代的解之间的相对误差,并用于判断循环是否停止.值得关注的是,整个算法的核心环节即步骤d),是有关本文模型(14)的凸优化求解过程,具体步骤如下. 模型利用外点罚函数法引入正数M,本文取M1,其放大系数取为 5,将式(15)转化为以下无约束问题 其中 式(38)中,I是大小为 2m×1 的单位向量. 其中,V(z)(min(0,z1),···,min(0,z2m))T. 其中,步长因子 下降方向 综上,本文提出的基于非凸复合函数的稀疏信号恢复算法(Non-convex composite sparse,NCCS)参考了文献[23]中的SCSA 算法,主要包括三个部分.一是算法的初始值选择,取值为L1范数最小化问题的解,参考文献[29],其计算量为O(m3).二是无约束问题的求解,通过外点罚函数法和共轭梯度法迭代求解最优值.由式(39)~式(44)可以看出,第二部分每次迭代的主要操作是内循环的两部分矩阵乘法,即 计算复杂度分别为 O(4m+2mn)和O(4m2+4m2n),则第二部分的计算量为O(l(4m+2mn+4m2+4m2n)),其中l表示内循环的迭代次数.三是迭代结果的稀疏化,利用加权L1范数最小化[27]对凸优化结果进行稀疏化处理,其计算量为O(m3). 为验证本文提出的算法在重构性能上的优越性,本节设计了几组有关SL0 算法[21]、BP 算法[15]、IRLS算法[16]、SCSA 算法[23]和本文介绍的NCCS 这5 种算法在重构性能上的对照实验.在仿真实验中,感知矩阵A和稀疏原信号x的具体取值为:矩阵A的大小取为 250×500,其中矩阵元素服从零均值、单位方差的高斯分布,矩阵的列具有单位L2范数;稀疏原信号x的维数取为 500,非零分项服从正态分布.实验将讨论信号稀疏度在区间 [20,110] 范围内各算法的重构情况.对于等式约束Axb,在已知感知矩阵A和测量向量b的情况下,分别利用上述5 种算法对稀疏原信号进行 100 次仿真实验,讨论算法的平均重构性能.为展示本文所提出的模型相对于最新文献[23]所提算法的先进性,本文对5 种算法采用了与文献[23]相同的参数选择,即 1)对SL0算法:令mu2,σmin10−4,c0.8,L8. 2)对IRLS 算法:令p0.5. 3)对BP 算法:令l11.0.1. 4)对SCSA 算法:令ε110−3,ε210−2,c 5)本文NCCS 算法:令ε110−3,ε210−2,ε310−1,c0.1,σ0min{2‖x0‖0,α},其中α是待定数.仿真实验一将给出模拟实验,以获得最佳实验数值. 实验中的重构性能包括: 1)重构信噪比(Signal noise ratio): 2)重构误差(Mean square error): 3)归一化均方差(Normalized mean square error): 4)支撑集恢复成功率(Recovery success rate of the support set): 仿真实验一.待定数α的最佳选值. 首先对NCCS 算法中待定数α进行模拟实验,观察不同大小的数值α对算法运行时间的影响,以获得更优的实验参数.为节省计算时长,考虑α大小为 0.1 到 0.9,间隔为 0.1,分别进行 100 次仿真实验.从图3 可以看出,各α值对算法运行时间的影响差距不大,总体趋势是算法运行时间随α的增加而减少;在α0.8时,算法在稀疏度k ≤100 时皆能保证运行时间最短.信号的稀疏度k是指信号向量中非零元素的个数,为便于编程,在后续实验中待定数α全部选定为0.8. 图3 待定数 α 对NCCS 算法运行时间的影响Fig.3 The influence of undetermined number α on the running time of NCCS algorithm 仿真实验二.NCCS 算法对稀疏原信号重构的实验. 图4 是稀疏原信号以及由NCCS 算法获得的恢复信号的仿真结果.图4 的稀疏度取值为k65.由图4 可见,恢复信号和稀疏原信号基本吻合,实验结果显示算法的重构误差为 2.6933× 10−17. 由此可以看出,本文提出的算法恢复出的稀疏信号很接近稀疏原信号. 图4 NCCS 算法的一维信号重构仿真图,信号大小为500×1,稀疏度为65Fig.4 One-dimensional signal reconstruction simulation diagram of NCCS algorithm,the signal size is 500 × 1,the sparsity is 65 仿真实验三.各算法的重构性能和稀疏度的变化关系. 图5 为5 组实验算法的重构误差 (MSE) 和稀疏度k的变化关系.其中IRLS 算法的重构误差最高;由于最速下降法在迭代过程中存在“锯齿效应”[30],实验中SL0 算法的重构误差也很大,且SL0 与BP、SCSA 这3 种算法都存在重构误差随着稀疏度的增加而增大的趋势;而NCCS 算法的重构误差相对最小,整体变化较稳定. 图5 SL0、IRLS、BP、SCSA、NCCS 5 种算法的重构误差和稀疏度的变化关系Fig.5 The relationship between the reconstruction error and sparsity of the five algorithms of SL0,IRLS,BP,SCSA,and NCCS 图6 表示随着稀疏度在区间 [20,110] 的等量增加,5 种算法的重构信噪比 (SNR) 的变化情况.其中SL0、BP 和IRLS 3 种算法的稀疏度越高,重构信噪比越低;NCCS 算法与SCSA 算法的重构信噪比在稀疏度区间 [20,110] 上表现较稳定.在实验的各组稀疏度下,NCCS 算法的重构信噪比远高于SL0、BP 和IRLS 这3 种算法,略高于SCSA 算法.所以使用NCCS 算法对信号的恢复精确度有一定的提高. 图6 SL0、IRLS、BP、SCSA、NCCS 5 种算法的重构信噪比和稀疏度的变化关系Fig.6 The relationship between the reconstructed signalto-noise ratio and sparsity of the five algorithms of SL0,IRLS,BP,SCSA,and NCCS 图7 展示5 种算法的重构运行时间和稀疏度k的变化关系.实验结果显示各算法的运行时间随稀疏度的增大而增加,稀疏度区间在 [20,90] 时,各算法的实验平均运行时间能保持在 2 s 以内.在稀疏度k >90 后,SCSA 算法重构运行时间迅速增加;当稀疏度k >120 后,该算法的平均重构运行时间不低于 20s.本文提出的NCCS 算法由于参数σ值的多次衰减导致算法进行多次迭代,因此也造成了运行时间相较于剩下的3 种算法要高,但对比最新文献[23]的SCSA 算法,NCCS 算法有更好的实验效果. 图7 SL0、IRLS、BP、SCSA、NCCS 5 种算法的运行时间和稀疏度的变化关系Fig.7 The relationship between the running time and sparsity of the five algorithms of SL0,IRLS,BP,SCSA,and NCCS 图8 是各算法的支撑集恢复成功率 (RSS) 和稀疏度k的变化关系.实验结果显示SL0、BP 和IRLS这3 种算法的稀疏向量支撑集恢复成功率随稀疏度的增加而下降,SCSA 算法在稀疏度k100、k110时,其支撑集恢复成功率分别为RSS0.9980、RSS0.9886,考虑为实验次数的不足而出现的偏差.相比之下,在NCCS 算法的重构仿真实验中,RSS值保持稳定,信号的支撑集在整个实验区间内实现完全恢复. 图8 SL0、IRLS、BP、SCSA、NCCS 5 种算法的支撑集恢复成功率和稀疏度的变化关系Fig.8 The relationship between the recovery success rate of the support set and sparsity of the five algorithms of SL0,IRLS,BP,SCSA,and NCCS 图9 以及表1 分别为实验中5 组算法恢复向量的归一化均方差 (NMSE) 和稀疏度k的变化关系图像曲线和具体数值记录.由图9 和表1 可见,NCCS算法和SCSA 算法的实验结果远小于SL0算法、BP算法和IRLS 算法的实验值. 表1 5 种算法的归一化均方差的数值记录Table 1 Numerical records of the normalized mean square error of five algorithms 图9 SL0、IRLS、BP、SCSA、NCCS 5 种算法的归一化均方差和稀疏度的变化关系Fig.9 The relationship between the normalized mean square error and sparsity of the five algorithms of SL0,IRLS,BP,SCSA,and NCCS 综上所述,本文提出的NCCS 算法的综合重构性能要比实验的对照算法好,所以利用NCCS 算法能更好地恢复稀疏信号向量. 本文运用MM 优化、外点罚函数法、共轭梯度法等方法,借鉴文献[23]提出的SCSA 算法思想,提出了一种新的稀疏信号重构算法,称为NCCS 算法.该算法利用逼近性能更优的非凸复合指数函数实现对L0范数的逼近.仿真实验表明,本文所提出的NCCS 算法不仅有效可行,而且在无噪声情况下,对比SL0、IRLS、BP、SCSA 这4 种算法,NCCS 算法在稀疏信号恢复实验中表现出更优越的重构性能.1 一种用于逼近 L0 范数的非凸复合指数泛函

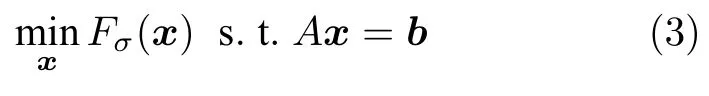
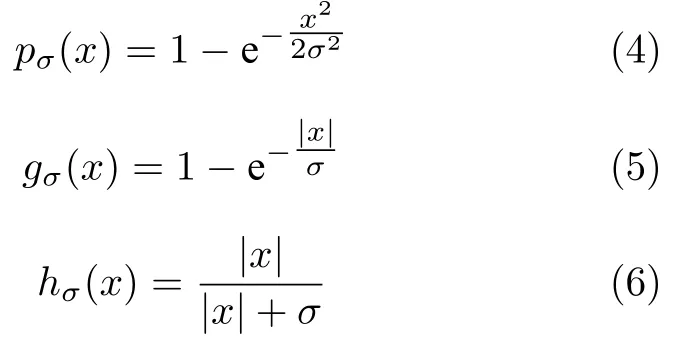

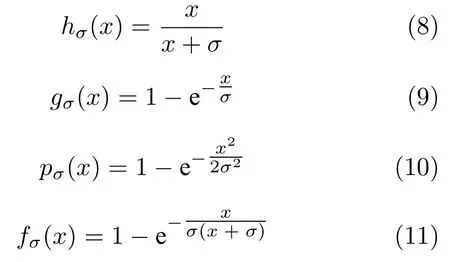


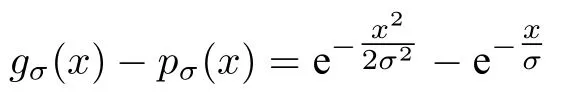
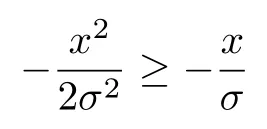

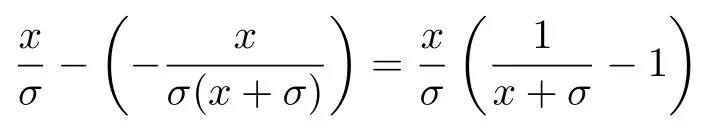

2 基于复合指数函数的稀疏模型

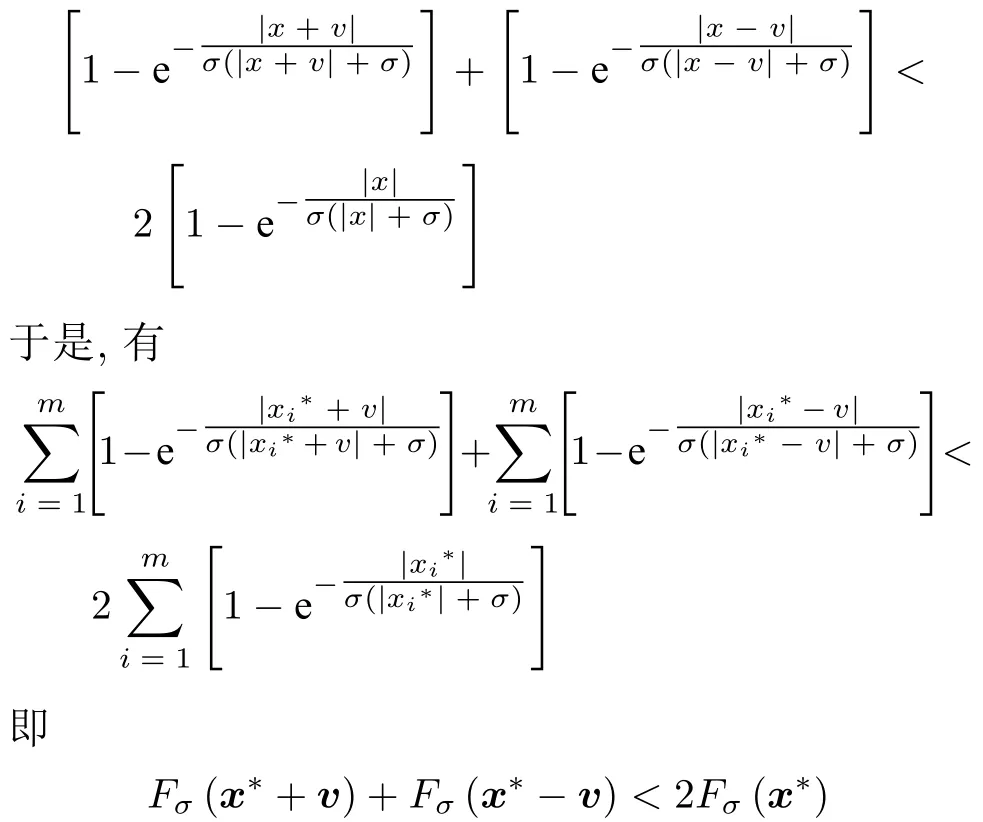
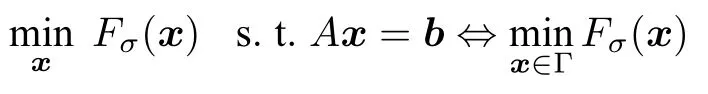

3 模型转换

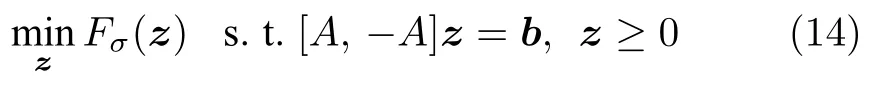
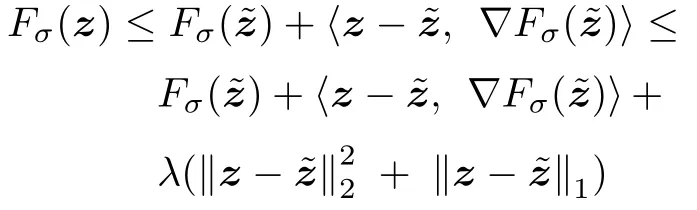

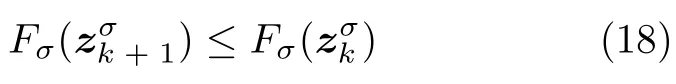


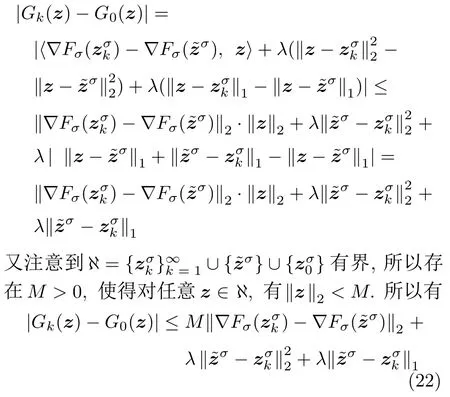

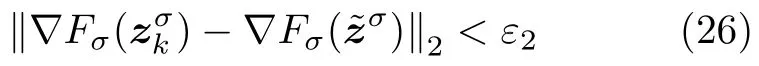
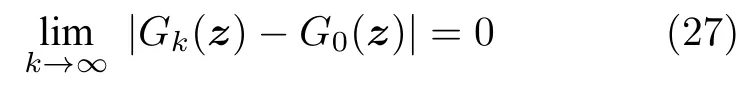
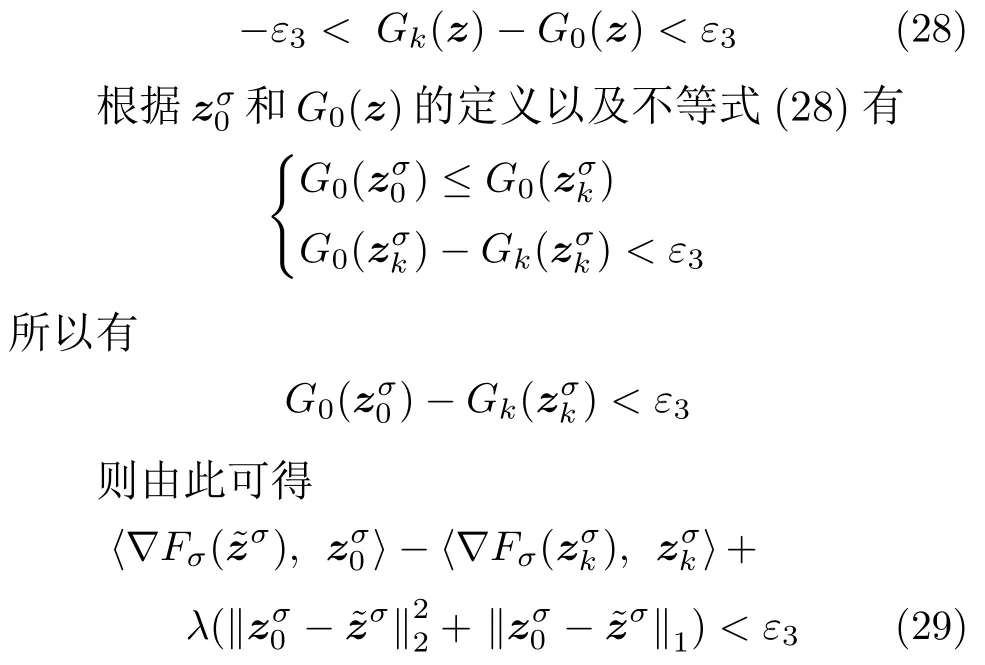
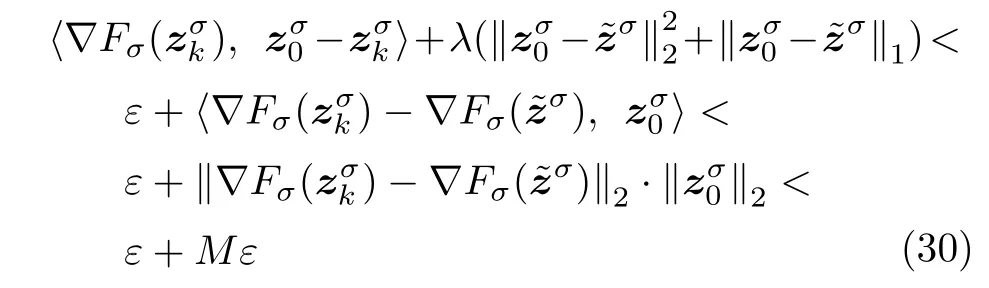
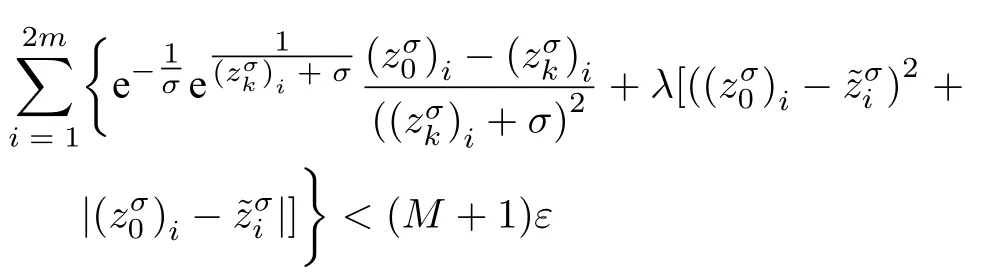
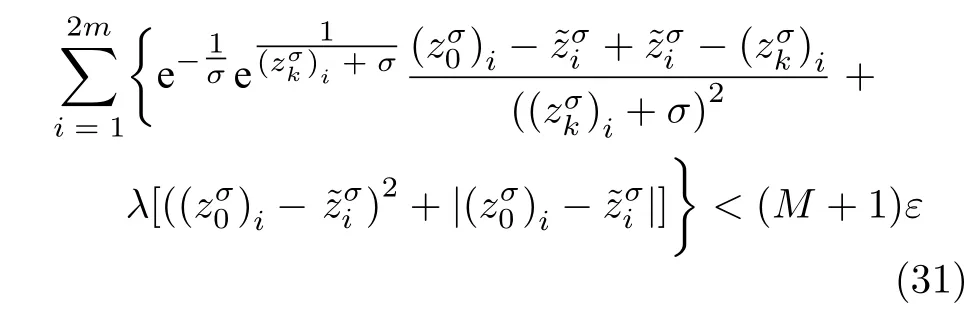





4 算法设计


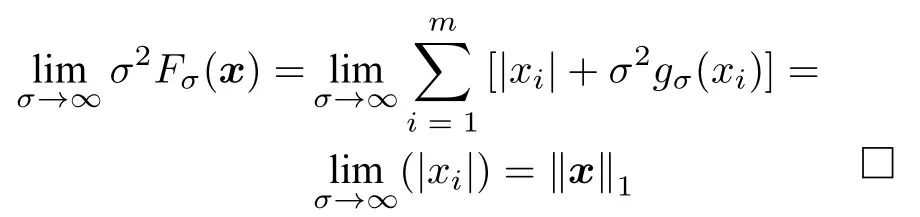
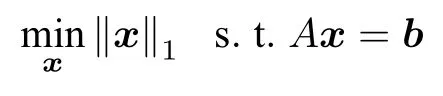

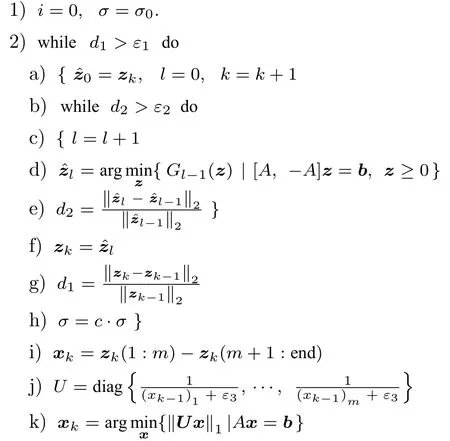
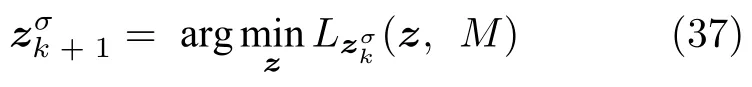
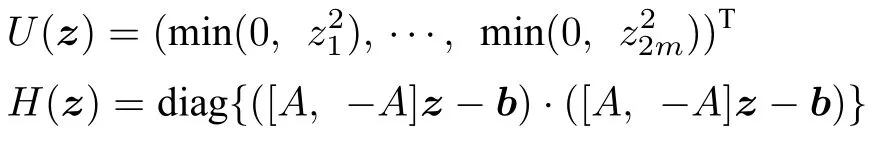
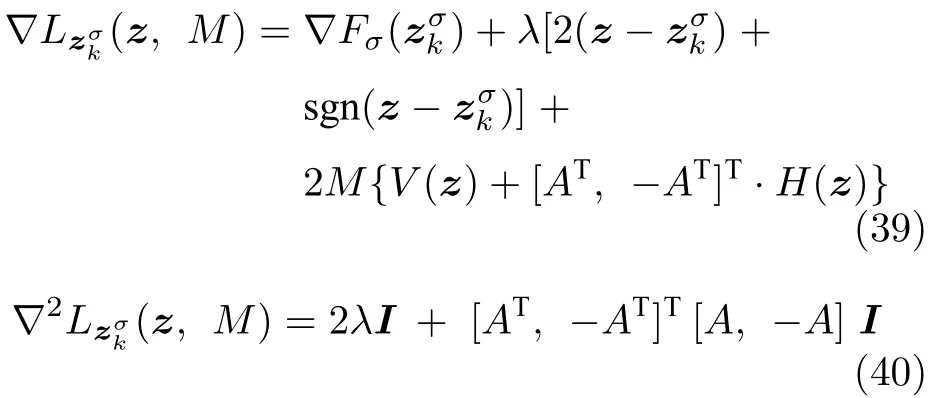
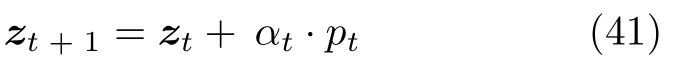
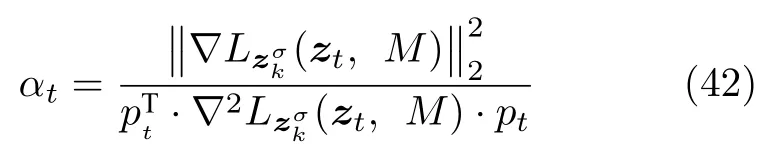
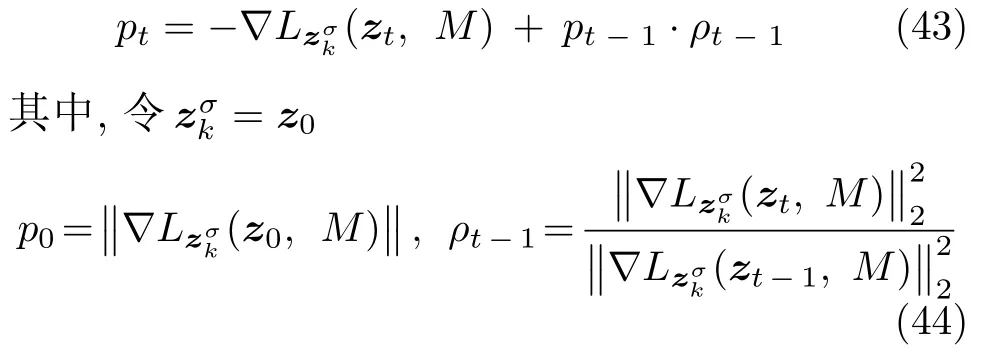
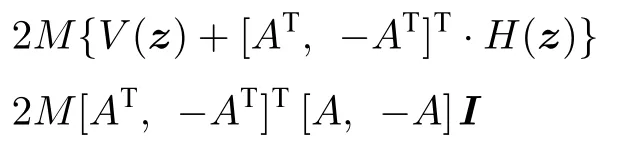
5 实验仿真与结果分析
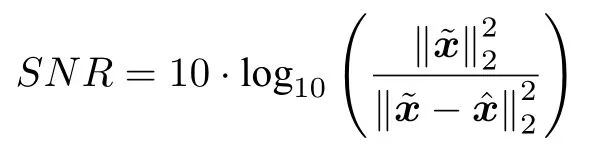
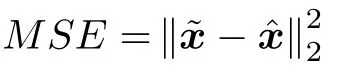
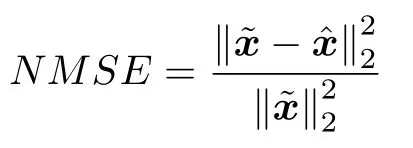
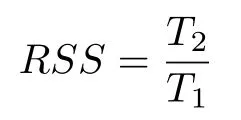
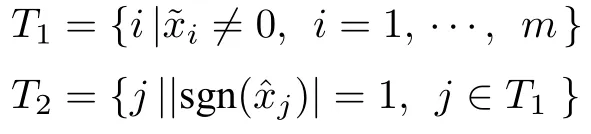



6 结论

