基于低秩约束的熵加权多视角模糊聚类算法
张嘉旭 王 骏 ,2 张春香 林得富 周 塔 王士同
随着多样化信息获取技术的发展,人们可以从不同途径或不同角度来获取对象的特征数据,即多视角数据.多视角数据包含了同一对象不同角度的信息.例如:网页数据中既包含网页内容又包含网页链接信息;视频内容中既包含视频信息又包含音频信息;图像数据中既涉及颜色直方图特征、纹理特征等图像特征,又涉及描述该图像内容的文本.多视角学习能有效地对多视角数据进行融合,避免了单视角数据数据信息单一的问题[1−4].
多视角模糊聚类是一种有效的无监督多视角学习方法[5−7].它通过在多视角聚类过程中引入各样本对不同类别的模糊隶属度来描述各视角下样本属于该类别的不确定性程度.经典的工作有:文献[8]以经典的单视角模糊C 均值(Fuzzy C-means,FCM)算法作为基础模型,利用不同视角间的互补信息确定协同聚类的准则,提出了Co-FC (Collaborative fuzzy clustering)算法;文献[9]参考文献[8]的协同思想提出Co-FKM (Multiview fuzzy clustering algorithm collaborative fuzzy K-means)算法,引入双视角隶属度惩罚项,构造了一种新型的无监督多视角协同学习方法;文献[10]借鉴了Co-FKM和Co-FC 所使用的双视角约束思想,通过引入视角权重,并采用集成策略来融合多视角的模糊隶属度矩阵,提出了WV-Co-FCM (Weighted view collaborative fuzzy C-means) 算法;文献[11]通过最小化双视角下样本与聚类中心的欧氏距离来减小不同视角间的差异性,基于K-means 聚类框架提出了Co-K-means (Collaborative multi-view K-means clustering)算法;在此基础上,文献[12]提出了基于模糊划分的TW-Co-K-means (Two-level weighted collaborative K-means for multi-view clustering)算法,对Co-K-means 算法中的双视角欧氏距离加入一致性权重,获得了比Co-K-means 更好的多视角聚类结果.以上多视角聚类方法都基于成对视角来构造不同的正则化项来挖掘视角之间的一致性和差异性信息,缺乏对多个视角的整体考虑.
一致性和差异性是设计多视角聚类算法需要考虑的两个重要原则[10−14].一致性是指在多视角聚类过程中,各视角的聚类结果应该尽可能保持一致.在设计多视角聚类算法时,往往通过协同、集成等手段来构建全局划分矩阵,从而得到最终的聚类结果[14−16].差异性是指多视角数据中的每个视角均反映了对象在不同方面的信息,这些信息互为补充[10],在设计多视角聚类算法时需要对这些信息进行充分融合.综合考虑这两方面的因素,本文拟提出新型的低秩约束熵加权多视角模糊聚类算法(Entropy-weighting multi-view fuzzy C-means with low rank constraint,LR-MVEWFCM),其主要创新点可以概括为以下3 个方面:
1)在模糊聚类框架下提出了面向视角一致性的低秩约束准则.已有的多视角模糊聚类算法大多基于成对视角之间的两两关系来构造正则化项,忽视了多个视角的整体一致性信息.本文在模糊聚类框架下从视角全局一致性出发引入低秩约束正则化项,从而得到新型的低秩约束多视角模糊聚类算法.
2) 在模糊聚类框架下同时考虑多视角聚类的一致性和差异性,在引入低秩约束的同时进一步使用面向视角差异性的多视角香农熵加权策略;在迭代优化的过程中,通过动态调节视角权重系数来突出具有更好分离性的视角的权重,从而提高聚类性能.
3)在模糊聚类框架下首次使用交替方向乘子法(Alternating direction method of multipliers,ADMM)[15]对LR-MVEWFCM 算法进行优化求解.在本文中,令N为样本总量,D为样本维度,K为视角数目,C为聚类数目,m为模糊指数.设xj,k表示多视角场景中第j个样本第k个视角的特征向量,j1,···,N,k1,···,K;vi,k表示第k个视角下,第i个聚类中心,i1,···,C;Uk[µij,k]表示第k个视角下的模糊隶属度矩阵,其中µij,k是第k个视角下第j个样本属于第i个聚类中心的模糊隶属度,i1,···,C,j1,···,N.
本文第1 节在相关工作中回顾已有的经典模糊C 均值聚类算法FCM 模型[17]和多视角模糊聚类Co-FKM 模型[9];第2 节将低秩理论与多视角香农熵理论相结合,提出本文的新方法;第3 节基于模拟数据集和UCI (University of California Irvine)数据集验证本文算法的有效性,并给出实验分析;第4 节给出实验结论.
1 相关工作
1.1 模糊C 均值聚类算法FCM
设单视角环境下样本x1,···,xN∈RD,U[µi,j]是模糊划分矩阵,V[v1,v2,···,vC] 是样本的聚类中心.FCM 算法的目标函数可表示为
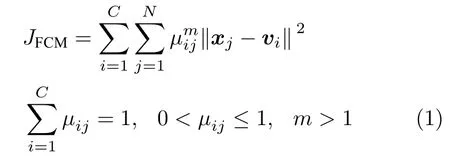
可得到JFCM取得局部极小值的必要条件为
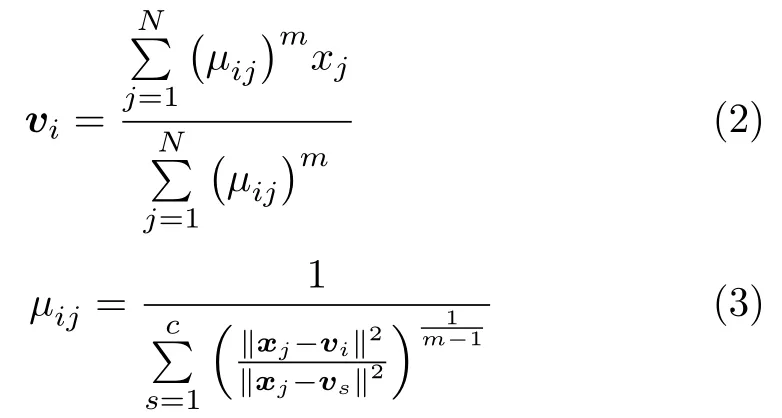
根据式(2)和式(3)进行迭代优化,使目标函数收敛于局部极小点,从而得到样本属于各聚类中心的模糊划分矩阵U.
1.2 多视角模糊聚类Co-FKM 模型
在经典FCM 算法的基础上,文献[9]通过引入视角协同约束正则项,对视角间的一致性信息加以约束,提出了多视角模糊聚类Co-FKM 模型.
多视角模糊聚类Co-FKM 模型需要满足如下条件:
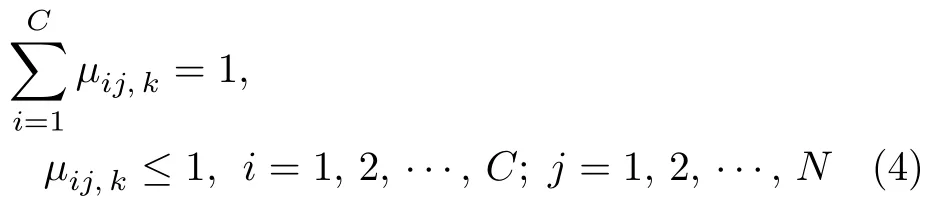
多视角模糊聚类Co-FKM 模型的目标函数JCo-FKM定义为
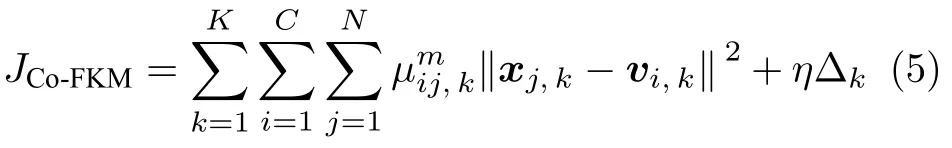
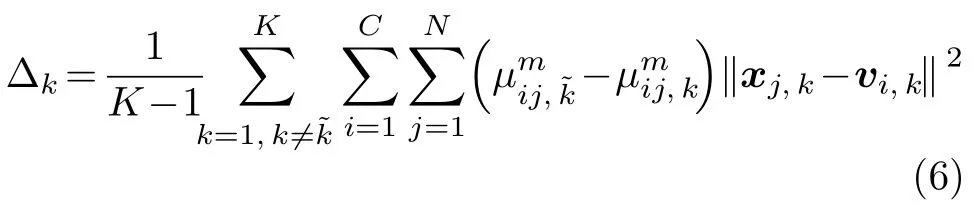
式(5)中,η表示协同划分参数; Δ 表示视角一致项,由式(6)可知,当各视角趋于一致时,Δ 将趋于0.
迭代得到各视角的模糊隶属度µij,k后,为了最终得到一个具有全局性的模糊隶属度划分矩阵,Co-FKM 算法对各视角下的模糊隶属度采用几何平均的方法,得到数据集的整体划分,具体形式为
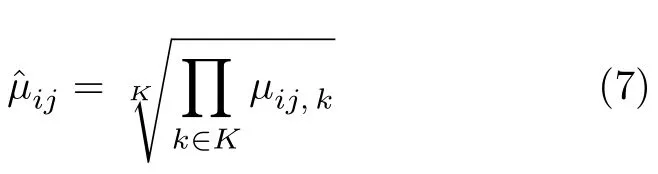
2 基于低秩约束的熵加权多视角模糊聚类算法
针对当前多视角模糊聚类算法研究中存在的不足,本文提出一种基于低秩约束的熵加权多视角模糊聚类新方法LR-MVEWFCM.一方面通过向多视角模糊聚类算法的目标学习准则中引入低秩约束项,在整体上控制聚类过程中各视角的一致性;另一方面基于香农熵理论,通过熵加权机制来控制各视角之间的差异性.同时使用交替方向乘子法对模型进行优化求解.
设多视角隶属度U1,···,UK融合为一个整体的隶属度矩阵U,将矩阵U的秩函数凸松弛为核范数,通过对矩阵U进行低秩约束,可以将多视角数据之间的一致性问题转化为核范数最小化问题进行求解,具体定义为

其中,U[U1··· UK]T表示全局划分矩阵,‖·‖∗表示核范数.式(8)的优化过程保证了全局划分矩阵的低秩约束.低秩约束的引入,可以弥补当前大多数多视角聚类算法仅能基于成对视角构建约束的缺陷,从而更好地挖掘多视角数据中包含的全局一致性信息.
目前已有的多视角的聚类算法在处理多视角数据时,通常默认每个视角平等共享聚类结果[11],但实际上某些视角的数据往往因空间分布重叠而导致可分性较差.为避免此类视角的数据过多影响聚类效果,本文拟对各视角进行加权处理,并构建香农熵正则项从而在聚类过程中有效地调节各视角之间的权重,使得具有较好可分离性的视角的权重系数尽可能大,以达到更好的聚类效果.

综上所述,本文作如下改进:首先,用本文提出的低秩约束全局模糊隶属度矩阵U;其次,计算损失函数时考虑视角权重wk,并加入视角权重系数的香农熵正则项.设U[U1··· UK]T;www[w1,···,wk,···,wK]表示K个视角下的视角权重.本文所构建LR-MVEWFCM 的目标函数为
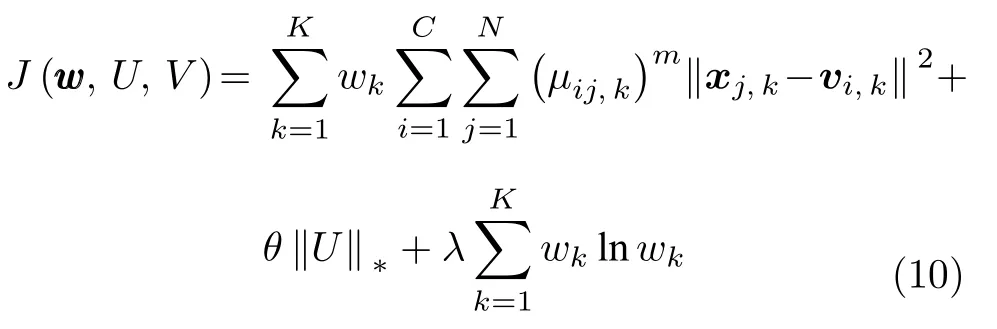
其中,约束条件为
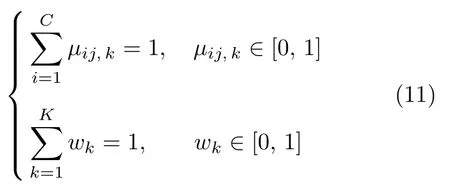
本文取模糊指数m2.
2.1 基于ADMM 的求解算法
在本节中,我们将使用ADMM 方法,通过交替方向迭代的策略来实现目标函数 (11) 的最小化.
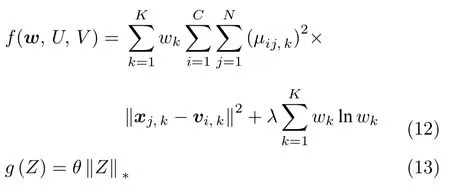
最小化式 (10) 可改写为如下约束优化问题:
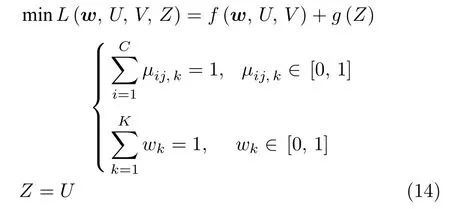
其求解过程可分解为如下几个子问题:
1)V-子问题.固定w和U,更新V为

2)U-子问题.固定w,Q和Z,更新U为
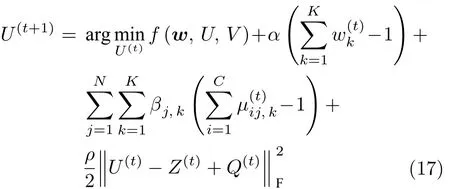
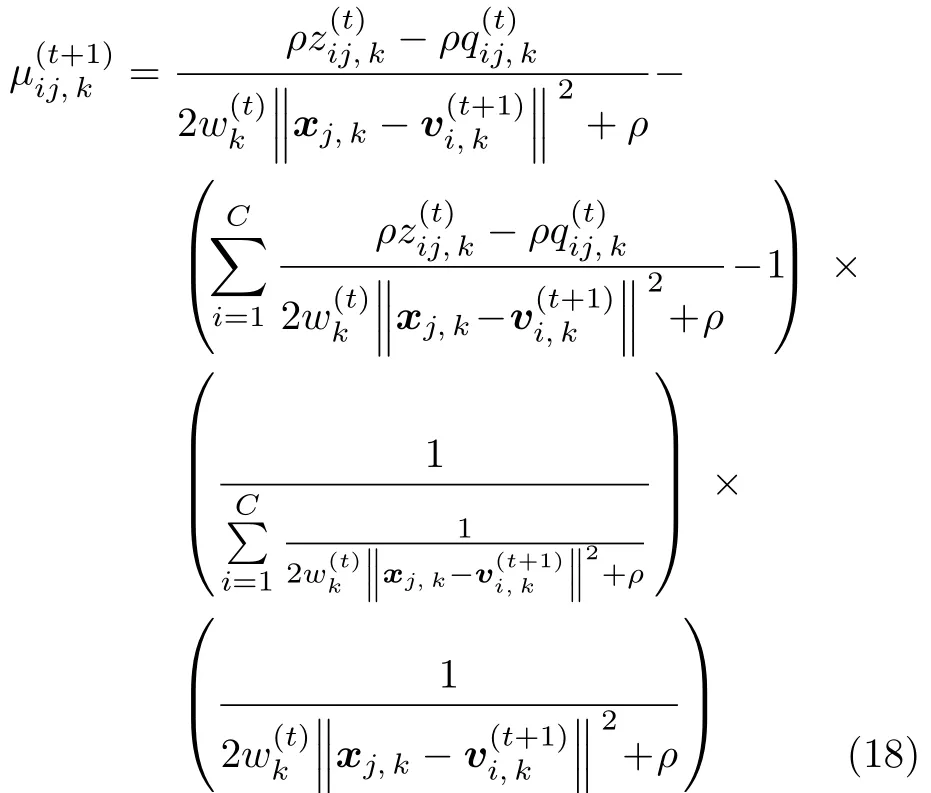
通过最小化式 (17),可得到U(t+1)的封闭解为
3)w-子问题.固定V和U,更新w为

4)Z-子问题.固定Q和U,更新Z为
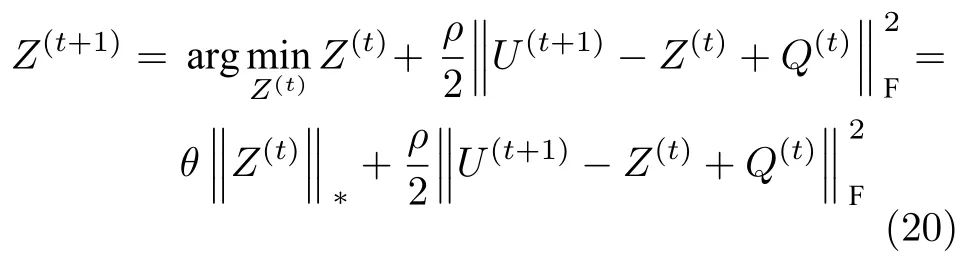
通过引入软阈值算子,可得式 (20) 的解为

其中,U(t+1)+Q(t)AΣBT为矩阵U(t+1)+Q(t)的奇异值分解,核范数的近邻算子可由软阈值算子Sθ/ρ(Σ)diag({max(0,σi −θ/ρ)})(i1,2,···,N)给出.
5)Q-子问题.固定Z和U,更新Q为

经过上述迭代过程,目标函数收敛于局部极值,同时得到不同视角下的模糊隶属度矩阵.本文借鉴文献[10]的集成策略,使用视角权重系数w[w1,···,wk,···,wK]和模糊隶属度矩阵U来构建具有全局特性的模糊空间划分矩阵

其中,wk,Uk分别表示第k个视角的视角权重系数和相应的模糊隶属度矩阵.
LR-MVEWFCM 算法描述如下:
输入.包含K(1≤k ≤K) 个视角的多视角样本集,其中任意一个视角对应样本集Xk{x1,k,···,xN,k},聚类中心C,迭代阈值ϵ,最大迭代次数T;
输出.各视角聚类中心模糊空间划分矩阵和各视角权重wk;
步骤1.随机初始化V(t),归一化U(t)及w(t),t0;
步骤2.根据式 (21)更新
步骤3.根据式 (23)更新U(t+1);
步骤4.根据式 (24) 更新
步骤5.根据式 (26)更新Z(t+1);
步骤6.根据式 (27)更新Q(t+1);
步骤7.如果<ϵ或者t>T,则算法结束并跳出循环,否则,返回步骤2;
步骤8.根据步骤7 所获取的各视角权重wk及各视角下的模糊隶属度Uk,使用式 (23)计算
2.2 讨论
2.2.1 与低秩约束算法比较
近年来,基于低秩约束的机器学习模型得到了广泛的研究.经典工作包括文献[16]中提出LRR(Low rank representation)模型,将矩阵的秩函数凸松弛为核范数,通过求解核范数最小化问题,求得基于低秩表示的亲和矩阵;文献[14]提出低秩张量多视角子空间聚类算法(Low-rank tensor constrained multiview subspace clustering,LT-MSC),在各视角间求出带有低秩约束的子空间表示矩阵;文献 [18] 则进一步将低秩约束引入多模型子空间聚类算法中,使算法模型取得了较好的性能.本文将低秩约束与多视角模糊聚类框架相结合,提出了LR-MVEWFCM 算法,用低秩约束来实现多视角数据间的一致性.本文方法可作为低秩模型在多视角模糊聚类领域的重要拓展.
2.2.2 与多视角Co-FKM 算法比较
图1 和图2 分别给出了多视角Co-FKM 算法和本文LR-MVEWFCM 算法的工作流程.
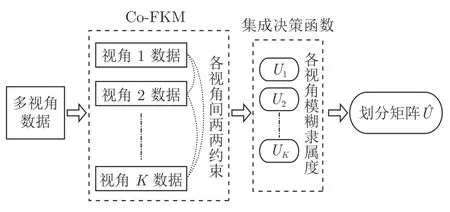
图1 Co-FKM 算法处理多视角聚类任务工作流程Fig.1 Co-FKM algorithm for multi-view clustering task

图2 LR-MVEWFCM 算法处理多视角聚类任务工作流程Fig.2 LR-MVEWFCM algorithm for multi-view clustering task
本文算法与经典的多视角Co-FKM 算法在多视角信息的一致性约束和多视角聚类结果的集成策略上均有所不同.在多视角信息的一致性约束方面,本文将Co-FKM 算法中的视角间两两约束进一步扩展到多视角全局一致性约束;在多视角聚类结果的集成策略上,本文不同于Co-FKM 算法对隶属度矩阵简单地求几何平均值的方式,而是将各视角隶属度与视角权重相结合,构建具有视角差异性的集成决策函数.
3 实验与分析
3.1 实验设置
本文采用模拟数据集和UCI 中的真实数据集进行实验验证,选取FCM[17]、CombKM[19]、Co-FKM[9]和Co-Clustering[20]这4 个聚类算法作为对比算法,参数设置如表1 所示.实验环境为:Intel Core i5-7400 CPU,其主频为2.3 GHz,内存为8 GB.编程环境为MATLAB 2015b.

表1 参数定义和设置Table 1 Parameter setting in the experiments
本文采用如下两个性能指标对各算法所得结果进行评估.
1) 归一化互信息(Normalized mutual information,NMI)[10]
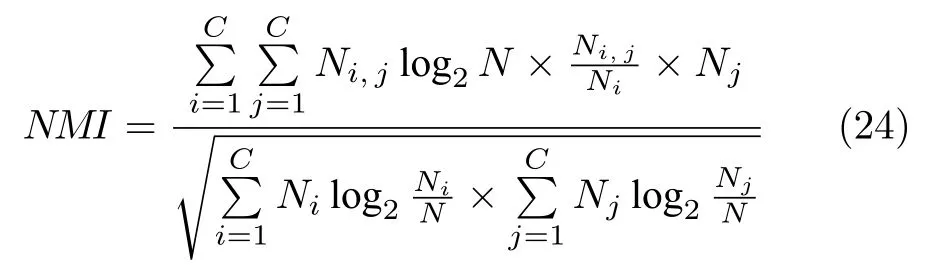
其中,Ni,j表示第i类与第j类的契合程度,Ni表示第i类中所属样本量,Nj表示第j类中所属样本量,而N表示数据的样本总量;
2) 芮氏指标(Rand index,RI)[10]
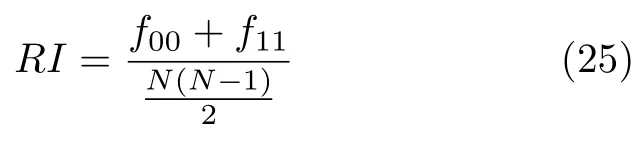
其中,f00表示具有不同类标签且属于不同类的数据配对点数目,f11则表示具有相同类标签且属于同一类的数据配对点数目,N表示数据的样本总量.以上两个指标的取值范围介于 [0,1] 之间,数值越接近1,说明算法的聚类性能越好.为了验证算法的鲁棒性,各表中统计的性能指标值均为算法10次运行结果的平均值.
3.2模拟数据集实验
为了评估本文算法在多视角数据集上的聚类效果,使用文献[10]的方法来构造具有三维特性的模拟数据集A(x,y,z),其具体生成过程为:首先在MATLAB 环境下采用正态分布随机函数normrnd构建数据子集A1(x,y,z),A2(x,y,z) 和A3(x,y,z),每组对应一个类簇,数据均包含200 个样本.其中第1 组与第2 组数据集在特征z上数值较为接近,第2 组与第3 组数据集在特征x上较为接近;然后将3 组数据合并得到集合A(x,y,z),共计600 个样本;最后对数据集内的样本进行归一化处理.我们进一步将特征x,y,z按表2 的方式两两组合,从而得到多视角数据.

表2 模拟数据集特征组成Table 2 Characteristic composition of simulated dataset
将各视角下的样本可视化,如图3 所示.
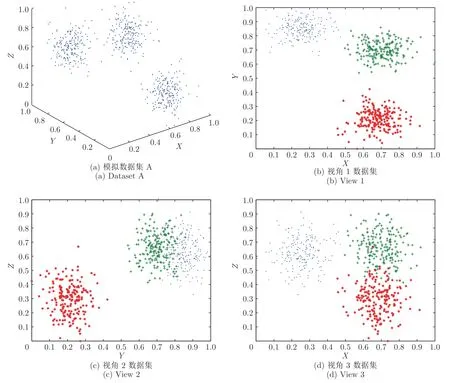
图3 模拟数据集及各视角数据集Fig.3 Simulated data under multiple views
通过观察图3 可以发现,视角1 中的数据集在空间分布上具有良好的可分性,而视角2 和视角3的数据在空间分布上均存在着一定的重叠,从而影响了所在视角下的聚类性能.通过组合不同视角生成若干新的数据集,如表3 所示,并给出了LRMVEWFCM 重复运行10 次后的平均结果和方差.

表3 模拟数据实验算法性能对比Table 3 Performance comparison of the proposed algorithms on simulated dataset
对比LR-MVEWFCM 在数据集1~3 上的性能,我们发现本文算法在视角1 上取得了最为理想的效果,在视角3 上的性能要优于视角2,这与图3中各视角数据的空间可分性是一致的.此外,将各视角数据两两组合构成新数据集4~6 后,LRMVEWFCM 算法都得到了比单一视角更好的聚类效果,这都说明了本文采用低秩约束来挖掘多视角数据中一致性的方法,能够有效提高聚类性能.
基于多视角数据集7,我们进一步给出本文算法与其他经典聚类算法的比较结果.
从表4 中可以发现,由于模拟数据集在某些特征空间下具有良好的空间可分性,所以无论是本文的算法还是Co-Clustering 算法、FCM 算法等算法均取得了很好的聚类效果,而CombKM 算法的性能较之以上算法则略有不足,分析其原因在于CombKM 算法侧重于挖掘样本之间的信息,却忽视了多视角之间的协作,而本文算法通过使用低秩约束进一步挖掘了多视角之间的全局一致性,因而得到了比CombKM 算法更好的聚类效果.

表4 模拟数据集7 上各算法的性能比较Table 4 Performance comparison of the proposed algorithms on simulated dataset 7
3.3 真实数据集实验
本节采用5 个UCI 数据集:1) Iris 数据集;2)Image Segmentation (IS) 数据集;3) Balance 数据集;4) Ionosphere 数据集;5) Wine 数据集来进行实验.由于这几个数据集均包含了不同类型的特征,所以可以将这些特征进行重新分组从而构造相应的多视角数据集.表5 给出了分组后的相关信息.
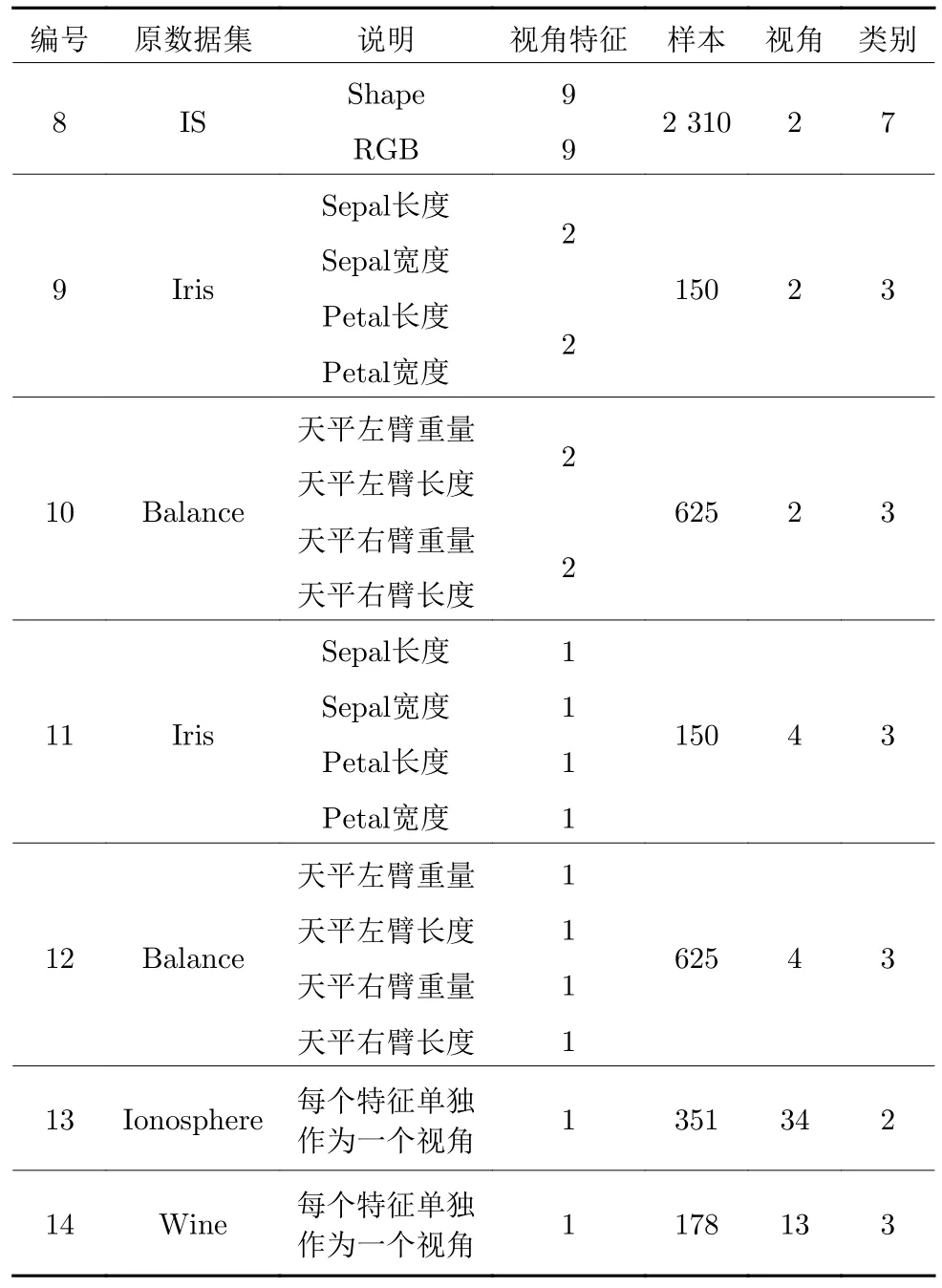
表5 基于UCI 数据集构造的多视角数据Table 5 Multi-view data constructded based on UCI dataset
我们在多视角数据集上运行各多视角聚类算法;同时在原数据集上运行FCM 算法.相关结果统计见表6 和表7.
通过观察表6 和表7 中的 NMI和 RI 指标值可知,Co-FKM 算法的聚类性能明显优于其他几种经典聚类算法,而相比于Co-FKM 算法,由于LRMVEWFCM 采用了低秩正则项来挖掘多视角数据之间的一致性关系,并引入多视角自适应熵加权策略,从而有效控制各视角之间的差异性.很明显,这种聚类性能更为优异和稳定,且收敛性的效果更好.表6 和表7 中的结果也展示了在IS、Balance、Iris、Ionosphere 和Wine 数据集上,其NMI 和RI 指标均提升3~5 个百分点,这也说明了本文算法在多视角聚类过程中的有效性.
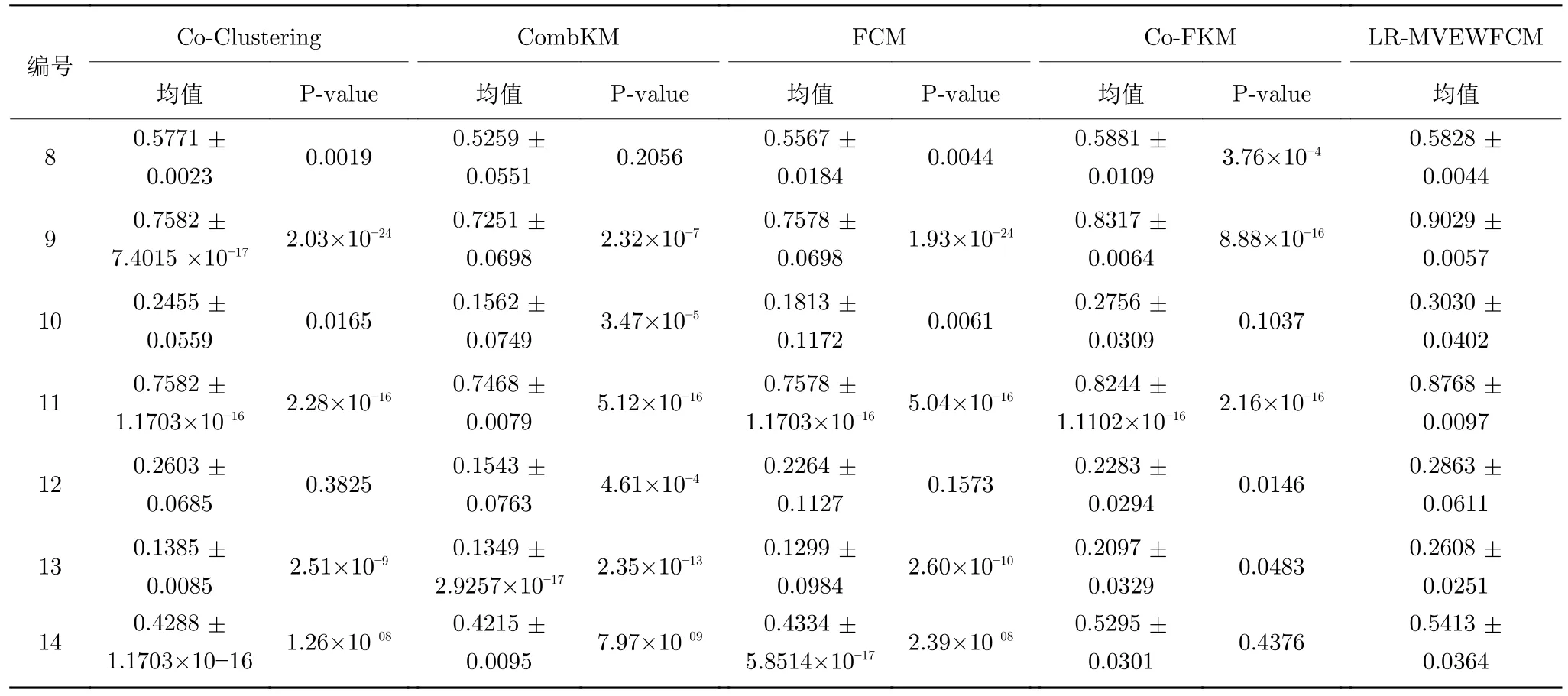
表6 5 种聚类方法的NMI 值比较结果Table 6 Comparison of NMI performance of five clustering methods
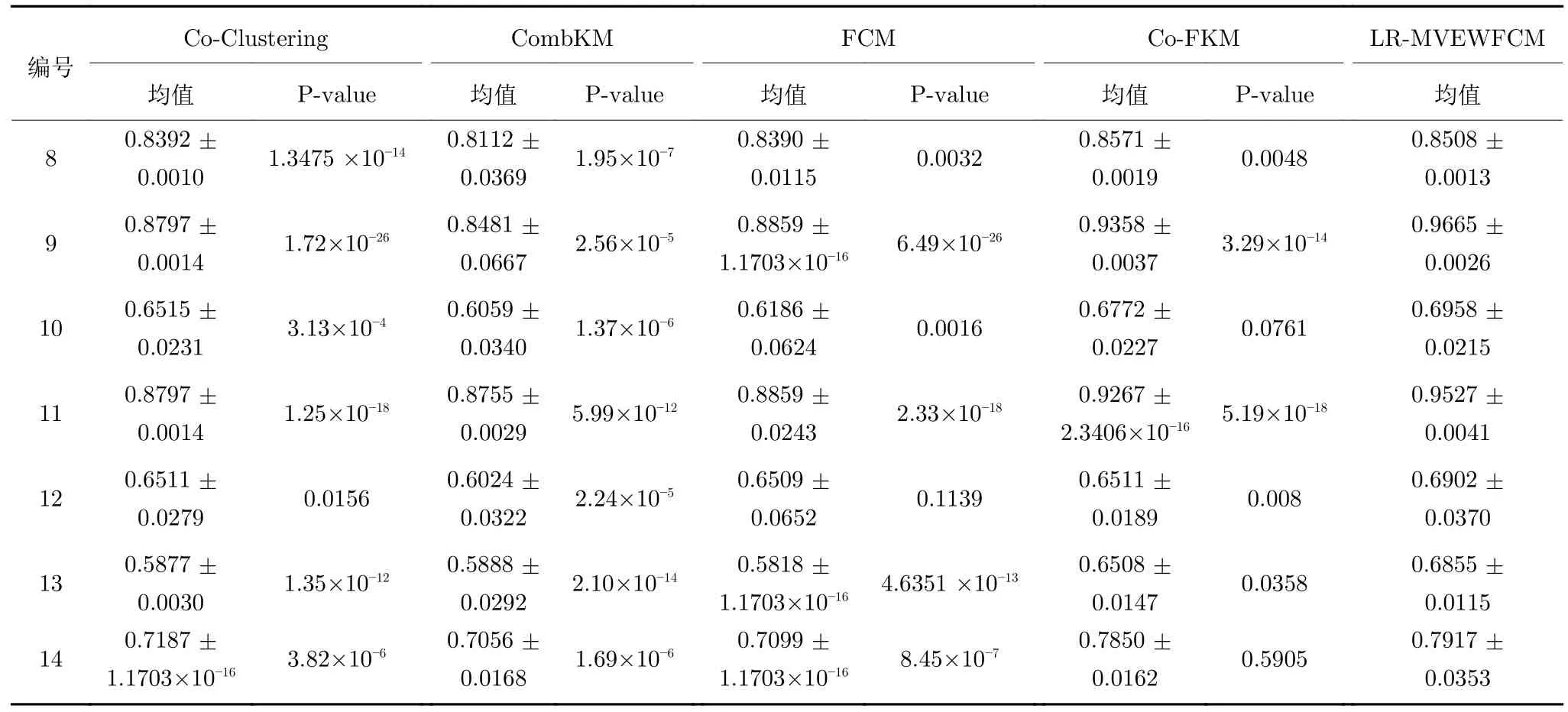
表7 5 种聚类方法的RI 值比较结果Table 7 Comparison of RI performance of five clustering methods
为进一步说明本文低秩约束发挥的积极作用,将LR-MVEWFCM 算法和MVEWFCM 算法共同进行实验,算法的性能对比如图4 所示.
从图4 中不难发现,无论在模拟数据集上还是UCI 真实数据集上,相比较MVEWFCM 算法,LRMVEWFCM 算法均可以取得更好的聚类效果.因此可见,LR-MVEWFCM 目标学习准则中的低秩约束能够有效利用多视角数据的一致性来提高算法的聚类性能.

图4 低秩约束对算法性能的影响(横坐标为数据集编号,纵坐标为聚类性能指标)Fig.4 The influence of low rank constraints on the performance of the algorithm (the X-coordinate is the data set number and the Y-coordinate is the clustering performance index)
为研究本文算法的收敛性,同样选取8 个数据集进行收敛性实验,其目标函数变化如图5 所示.
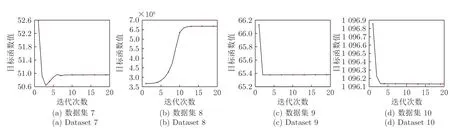
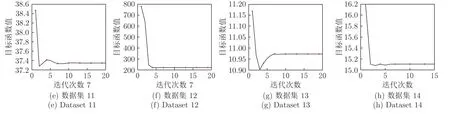
图5 LR-MVEWFCM 算法的收敛曲线Fig.5 Convergence curve of LR-MVEWFCM algorithm
从图5 中可以看出,本文算法在真实数据集上仅需迭代15 次左右就可以趋于稳定,这说明本文算法在速度要求较高的场景下具有较好的实用性.
综合以上实验结果,我们不难发现,在具有多视角特性的数据集上进行模糊聚类分析时,多视角模糊聚类算法通常比传统单视角模糊聚类算法能够得到更优的聚类效果;在本文中,通过在多视角模糊聚类学习中引入低秩约束来增强不同视角之间的一致性关系,并引入香农熵调节视角权重关系,控制不同视角之间的差异性,从而得到了比其他多视角聚类算法更好的聚类效果.
3.4 参数敏感性实验
LR-MVEWFCM 算法包含两个正则项系数,即视角权重平衡因子λ和低秩约束正则项系数θ,图6以LR-MVEWFCM 算法在模拟数据集7 上的实验为例,给出了系数从0 到1 000 过程中,算法性能的变化情况,当低秩正则项系数θ=0 时,即不添加此正则项,算法的性能最差,验证了本文加入的低秩正则项的有效性,当θ值变化过程中,算法的性能相对变化较小,说明本文算法在此数据集上对于θ值变化不敏感,具有一定的鲁棒性;而当香农熵正则项系数λ=0 时,同样算法性能较差,也说明引入此正则项的合理性.当λ值变大时,发现算法的性能也呈现变好趋势,说明在此数据集上,此正则项相对效果比较明显.
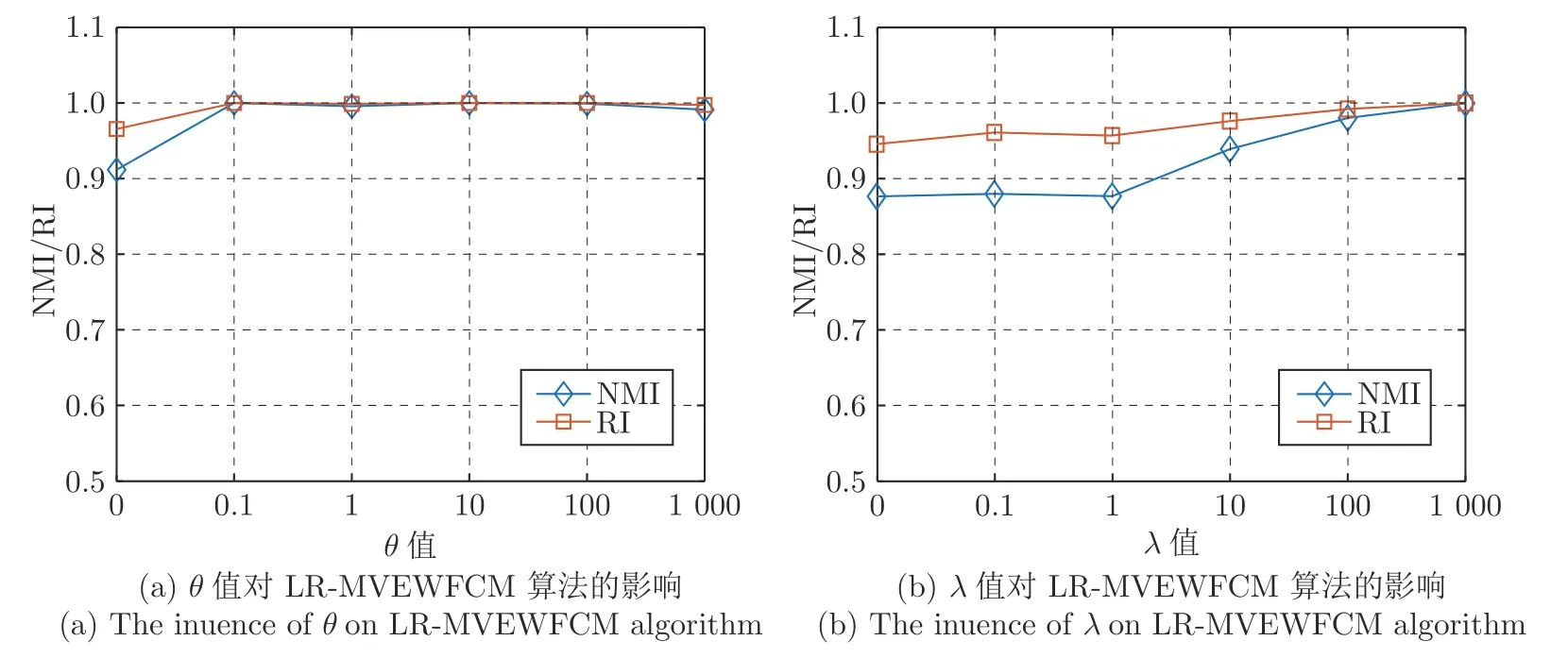
图6 模拟数据集7 上参数敏感性分析Fig.6 Sensitivity analysis of parameters on simulated dataset 7
4 结束语
本文从多视角聚类学习过程中的一致性和差异性两方面出发,提出了基于低秩约束的熵加权多视角模糊聚类算法.该算法采用低秩正则项来挖掘多视角数据之间的一致性关系,并引入多视角自适应熵加权策略从而有效控制各视角之间的差异性,从而提高了算法的性能.在模拟数据集和真实数据集上的实验均表明,本文算法的聚类性能优于其他多视角聚类算法.同时本文算法还具有迭代次数少、收敛速度快的优点,具有良好的实用性.由于本文采用经典的FCM 框架,使用欧氏距离来衡量数据对象之间的差异,这使得本文算法不适用于某些高维数据场景.如何针对高维数据设计多视角聚类算法,这也将是我们今后的研究重点.

