黏滞阻尼器对高速列车-大跨斜拉桥耦合系统的减震分析
郭文华,段彬鑫,张廷奎
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中铁第四勘察设计院集团有限公司 工程经济设计研究院,湖北 武汉 430063)
我国幅员辽阔,江河密布,且地处跨环太平洋地震带和地中海-喜马拉雅地震带,是一个地震高发国家[1]。随着我国高速铁路的蓬勃发展,越来越多的高铁线路需要跨越大江大河、高山峡谷,甚至海湾、海峡。大跨度斜拉桥凭借其较小自重、较大跨度和较高刚度得到了广泛的采用。黏滞阻尼器安装在斜拉桥塔梁或墩梁连接处,减隔震效果显著,且养护维修方便[2-5]。当地震发生时,尽管桥梁结构自身可能未发生严重破坏,但桥梁结构会将地震波通过钢轨传递到列车上,而高速铁路列车行车速度很快,对线路平顺性要求极高,列车也可能因剧烈的振动而脱轨,造成重大安全事故。
国内外学者通过理论分析、数值仿真、模型试验等方法对黏滞阻尼器的性能、高速列车-大跨度斜拉桥耦合振动、黏滞阻尼器对斜拉桥减震性能等问题进行了深入的研究。李小珍等[6]、郭文华等[7]采用时域分析法,进行了列车经过斜拉桥时的车桥空间耦合振动响应分析,评价了列车的运行安全性。韩艳等[8]、熊建珍等[9]、张骞等[10]研究了铁路斜拉桥在地震作用或横风作用下的车-桥耦合动力响应及列车走行性能。朱志辉等[11]分析了高速列车行驶引起的斜拉桥局部振动响应,研究表明大跨度斜拉桥由于整体自振频率低,车致振动显著,车-桥耦合问题不能忽视。关于黏滞阻尼器减震性能方面的研究,巫生平等[12]、Geng 等[13]、Soneji 等[14]建立斜拉桥有限元空间模型,对比了不同阻尼器布置方式的减震效果,并以桥梁关键部位的抗震能力为指标,对阻尼器的性能参数进行优化。Xu等[15]分别通过振动台试验和有限元建模研究大跨斜拉桥的地震响应,振动台试验表明黏性阻尼器能显著减少梁端位移,但对塔底弯矩的减小不明显。Zhong等[16]采用OPENSEES建立斜拉桥数值模型,通过系统易损性评估方法计算黏滞阻尼器参数优化值。吕龙等[17]通过施加制动力、移动荷载分别模拟列车制动作用和运行作用,探索了塔梁间设置黏滞阻尼器对抑制列车制动和运行引起梁体纵向振动的效果。
以往研究斜拉桥黏滞阻尼器减震效果时往往仅单独考虑地震作用,一般未建立用弹簧阻尼相连的多刚体列车模型,故未同时考虑高速列车运行引起的车致振动,亦不能对行车安全性进行评估。目前黏滞阻尼器对高速列车-大跨斜拉桥耦合系统减震效果的研究甚少。
本文基于ANSYS 和SIMPACK 联合仿真分析平台,以某主跨为400 m 的双塔双索面斜拉桥为例,建立地震作用下列车-轨道-斜拉桥-黏滞阻尼器耦合系统动力分析模型,考虑轨道不平顺和地震波作为激振源,开展地震作用下车桥耦合系统振动分析,研究地震强度和黏滞阻尼器参数对车桥动力响应的影响。
1 地震作用下列车-轨道-斜拉桥-黏滞阻尼器空间振动分析模型
1.1 列车动力学模型
基于多体动力学建立列车模型,将车辆简化为由车体、转向架和轮对等多个刚体以及一、二系悬挂系统组成的多刚体质量弹簧阻尼系统,每个刚体考虑伸缩、横摆、浮沉、侧滚、点头、摇头在内的6个自由度。其中,单节车辆模型包含1个车体、2个转向架和4 个轮对共7 个刚体,共有42 个自由度,其结构模型如图1所示。图中:Lc,Lb和Lw分别为车长、转向架中心距以及轴距,Kps,Cps和Kss,Css分别为一、二系悬挂系统的刚度和阻尼。
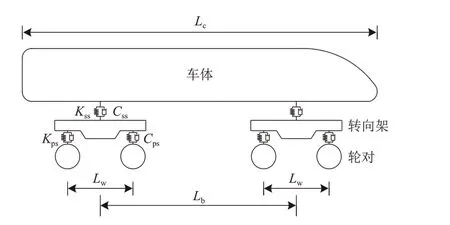
图1 车辆动力学模型示意图
1.2 桥梁、轨道动力学模型
采用ANSYS 建立大跨斜拉桥和轨道有限元分析模型。主梁、桥塔和辅助墩采用空间梁单元模拟,二期恒载采用主梁换算密度的形式模拟。斜拉索采用只受拉空间杆单元模拟,通过调整初应变设置成桥索力,并采用Ernst公式(1)修正拉索的弹性模量Eeq以考虑垂度效应的影响。
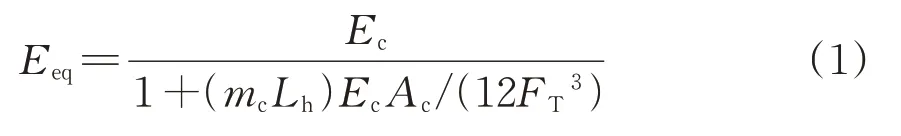
式中:Ec为拉索初始弹性模量;mc,Lh和Ac分别为拉索的两端点水平投影距离、单位长度质量和横截面积;FT为拉索索力。
球形钢支座刚度大、承载能力好,被广泛应用于铁路桥梁中。本文对支座不可活动方向的自由度进行主从约束、对可活动的自由度释放约束,以此模拟球形钢支座。
将轨道视为由离散弹性点支撑的Euler 梁,同样用空间梁单元模拟。钢轨通过扣件连接在主梁上,采用弹簧-阻尼器单元模拟梁轨连接关系,并输入横、竖向刚度和阻尼。
1.3 黏滞阻尼器力学模型
本文采用Maxwell非线性力学模型作为黏滞阻尼器计算模型,阻尼力Fd的大小为
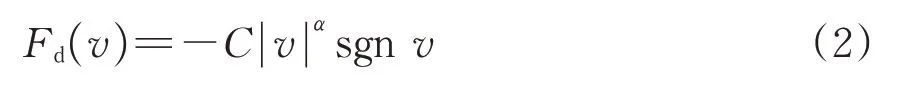
式中:C为阻尼系数;α为速度指数,一般取值为0.1~2.0,当α取1 时即为线性黏滞阻尼器;v为阻尼器冲程速度。
当速度指数较小时,黏滞阻尼器阻尼力的非线性特征明显,阻尼力在速度v接近0 时增大(或减小)较快,易引起仿真计算结果发散,本文采用正则化速度对阻尼器冲程速度进行修正,以提高计算的收敛性,具体如下。
无锡金利达生态科技有限公司是国内专业从事水生态修复工程技术研发及工程材料生产的高新技术企业,是水生态修复整体解决方案提供商。公司主营业务包括水生态修复、生态护岸工程的规划、设计、咨询;水生态修复工程技术及产品的研发、生产和销售;水生态修复工程施工技术的研究、推广和应用等。公司研发的“生态格网结构”系列产品销售额在国内市场遥遥领先,成为该行业领军企业。
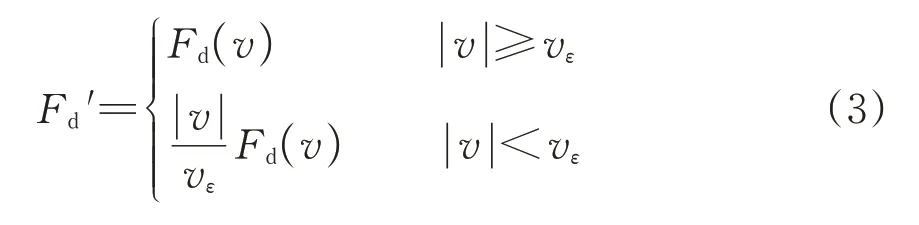
式中:Fd′为修正后的阻尼力;vε为设定的1个较小的临界速度,本文取0.001 m·s-1。
当黏滞阻尼器冲程速度小于vε时对阻尼力进行修正,使其平滑地降至0。
1.4 车-轨-桥耦合系统
轮轨接触关系是形成列车-轨道耦合系统的关键,包括轮轨接触几何关系以及轮轨力。其中轮轨力又含轮轨法向力和轮轨蠕滑力,轮轨法向力采用Hertz 弹性接触理论[18]计算,为考虑轮对的跳轨和挤压,假设轮轨的接触点之间有1 个单边弹簧-阻尼元件,轮轨法向力的表达式为
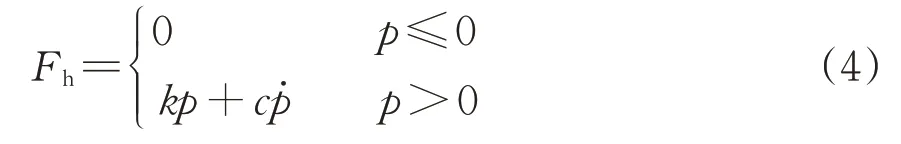
式中:p和分别为轮轨之间法向渗透量和法向渗透速度;k和c分别为弹簧的刚度和阻尼。
采用基于Kalker简化理论的FASTSIM 算法计算轮轨蠕滑力[19]。
将ANSYS 建立的斜拉桥、轨道有限元模型存储为编码数据库文件(Coded Database File),对模型进行子结构分析,导出包含模型刚度和质量矩阵的子结构矩阵文件(Substructure Matrices File),通过程序接口将其导入SIMPACK,生成对应的桥梁和轨道柔性体模型。以梁轨连接关系和轮轨接触关系作为桥梁、轨道、列车3 个子系统联系的纽带,形成车-轨-桥耦合系统力学模型。
轨道随机不平顺是车桥耦合系统的主要激励源之一,通过频域的功率谱密度函数生成空间域的轨道不平顺输入函数,并改变轮轨接触模块中所识别的轨道空间初始位置,实现轨道随机不平顺的输入。
1.5 地震动输入
在进行车-桥耦合系统地震响应分析时,采用直接求解法,除了地震波的加速度时程,还需知道速度和位移时程。为避免量测地震波加速度时程时包含的噪声在多次积分后被放大,本文采用最小二乘法对加速度时程进行基线修正,按照位移点在均值线两侧分布均匀和多项式阶数尽可能低的准则,采用三次多项式对加速度的均值线进行校正,再对其积分获得修正后的速度、位移时程曲线[20-21]。以El Centro 为例,修正前后的竖向地震波的加速度、速度和位移时程如图2—图4所示。可见,速度和位移时程的偏移在基线修正后有了明显的改观。
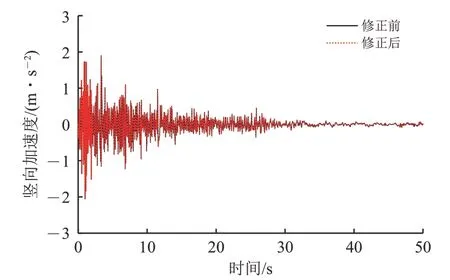
图2 修正前后地震波加速度时程曲线

图3 修正前后地震波竖向速度时程曲线
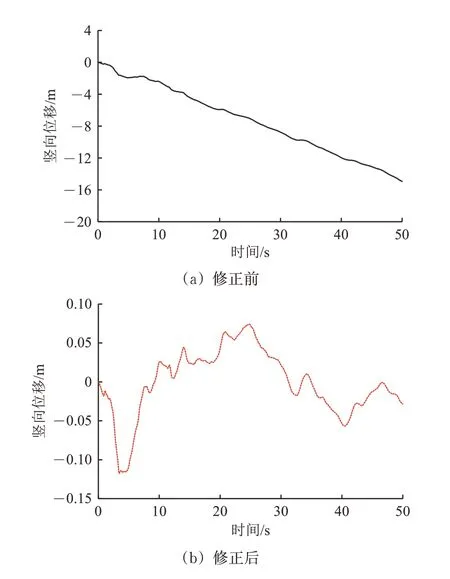
图4 修正前后地震波竖向位移时程曲线
在SIMPACK 中用一种质量、惯性矩均极小的虚刚体模拟墩底基础,建立与桥梁-轨道柔性体的约束关系,并让该虚刚体按照修正后的地震波加速度、速度和位移时程发生运动,从而实现地震动输入。
2 工程背景与计算条件
2.1 工程概况
以建设中的福厦高铁某大跨斜拉桥为例,该桥采用70 m+130 m+400 m+130 m+70 m双塔双索面钢混结合梁斜拉桥,建成后将成为世界首座设计时速350 km 的高速铁路跨海斜拉桥。桥梁两侧边跨各设有2 个辅助墩,总体布置如图5所示。主梁为混凝土桥面板与槽型钢箱梁组成的叠合梁结构,封闭箱形断面形式,梁宽17 m,风嘴宽4 m,梁高4.25 m。桥塔采用H 形混凝土索塔,塔底以上桥塔全高为160.254 m,主梁以上塔高109 m。主桥共设72 对斜拉索,空间双索面体系,扇形布置。桥面板及墩塔均采用C50 混凝土,钢箱梁采用Q345 钢材,斜拉索采用1 860 MPa 预应力钢绞线。桥梁阻尼采用Rayleigh 模式,阻尼比取2%。主桥采用半漂浮体系,在辅助墩和主塔的一侧设横向约束、纵向活动,在梁塔之间纵向设置黏滞阻尼器。支座及阻尼器布置方式如图6所示,图中:1#,3#,9#和11#为纵向活动支座;2#,4#,10#和12#为双向活动支座;5#和7#为纵向活动支座并设有纵向阻尼器;6#和8#为双向活动支座并设有纵向阻尼器。

图5 斜拉桥总体立面图
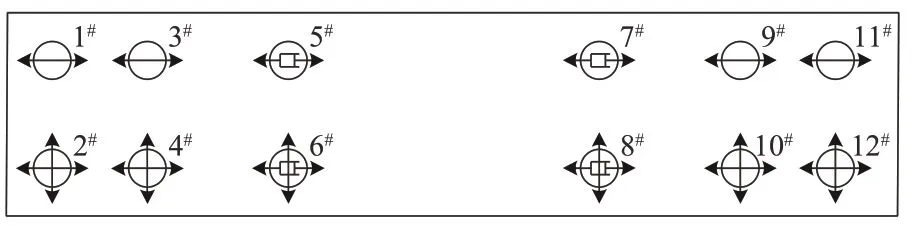
图6 全桥支座布置图
2.2 桥梁自振特性
采用ANSYS 和SIMPACK 分别对斜拉桥模型进行模态分析,桥梁自振频率及阵型见表1。由表1可知:ANSYS与SIMPACK 2种软件对于桥梁有限元模型自振特性的计算结果高度吻合,表明本文采用ANSYS 桥梁有限元模型生成柔性体输入文件,并导入到SIMPACK 平台完成桥梁建模的方法是正确的;该桥第1 阶模态为主梁1 阶横弯,横弯振型先于竖弯振型出现,表明桥梁的横向刚度要弱于竖向刚度,这符合一般铁路斜拉桥的特征。
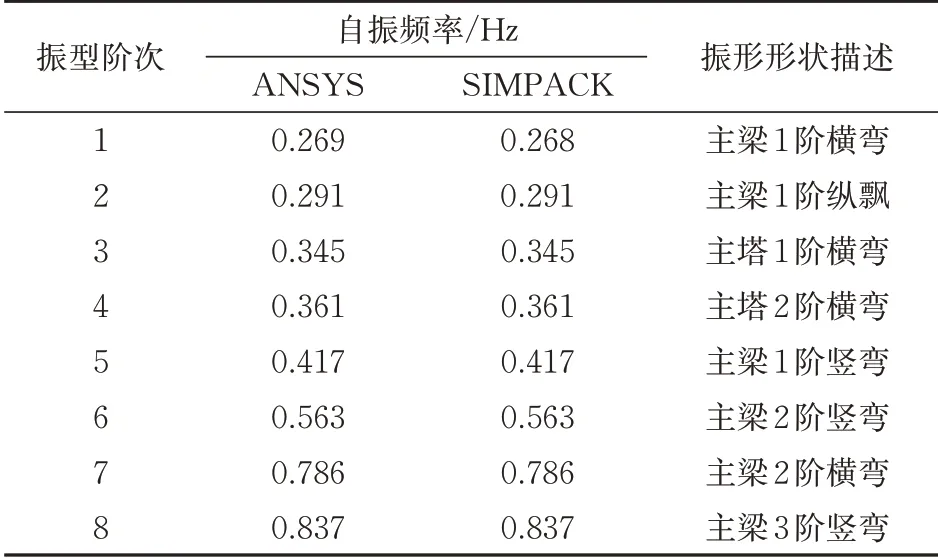
表1 泉州湾特大桥有限元模型前8阶自振特性
2.3 车辆和轨道模型参数
在进行高速列车-大跨斜拉桥耦合系统动力仿真分析时,采用ICE3 动车组,单列8 车编组(拖车+6×动车+拖车),车辆参数见文献[22]。轨道模型采用轨距为1 435 mm 的标准板式无砟轨道,标准60 km·m-1钢轨,扣件间距为0.6 m,扣件横、竖向刚度分别取60 和120 MN·m-1,扣件横、竖向阻尼分别取120和150 kN·s·m-1。轨道不平顺采用德国低干扰谱。
2.4 地震激励参数
本文采用修正后El Centro 地震波的水平南北向分量以及竖向分量作为车-轨-桥耦合系统动力分析的地震波。用横桥向加速度波幅值表示地震强度,竖桥向加速度波幅值取为横桥向的0.5倍。
3 地震强度对耦合系统动力响应的影响
为分析地震强度对车-轨-桥耦合系统振动响应的影响,假定车速为300 km·h-1,选取地震强度范围为0.06g~0.20g,按每隔0.02g为1 个工况,分别计算不同地震强度下的列车-桥梁空间振动响应,计算中假定桥梁结构始终处于弹性阶段。不同地震强度下列车和桥梁最大动力响应如图7所示。
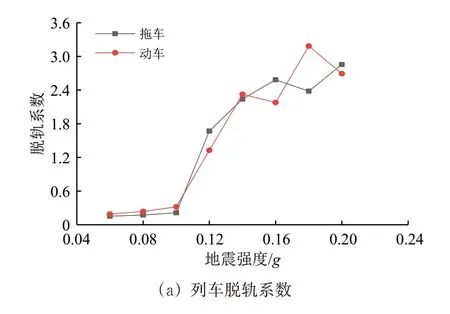
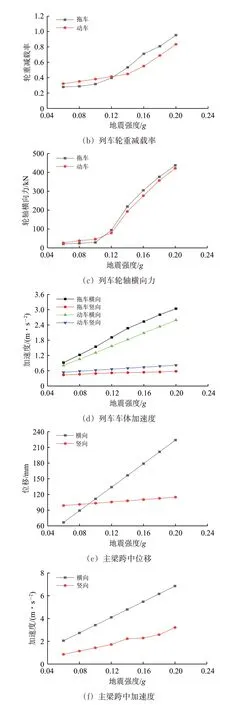
图7 不同地震强度下列车和桥梁动力响应
计算结果表明:随着地震强度的增加,列车的脱轨系数、轮重减载率、轮轴横向力和车体加速度呈增长趋势,列车脱轨系数和轮轴横向力在地震强度超过0.10g后增速明显加快,并且超过了安全限值,列车行车的安全性无法保证;桥梁主跨跨中位移、加速度均不断增大;无横向阻尼器时,地震作用对耦合系统横向响应的影响大于竖向。
4 黏滞阻尼器参数对耦合系统动力响应的影响
4.1 横向黏滞阻尼器布置方案
原设计方案主梁在纵桥向为半漂浮体系,梁塔之间仅设有纵向阻尼器限制主梁位移(见图6),考虑到横向地震可能对高速行车安全产生更不利影响,为研究黏滞阻尼器在横向减震体系中的作用,故解除辅助墩3#和9#处、主塔5#和7#处支座的横向约束,并采用横向黏滞阻尼器替换。
4.2 横向黏滞阻尼器参数的影响
黏滞阻尼器的耗能能力与速度指数α和阻尼系数C密切相关。为此,针对横向阻尼器布置方案开展阻尼器参数敏感性分析。保持列车车速为300 km·h-1,地震强度为0.1g不变,选择黏滞阻尼器的速度指数α分别为0.2,0.3,0.4,0.6 和0.8,阻尼系数C分别为2 000,4 000,6 000,8 000和10 000 kN·(m·s-1)-α,共组合25 个工况,进行耦合系统在地震作用下的动力响应分析。图8和图9分别给出了不同阻尼系数C、不同速度指数α组合下列车和桥梁的动力响应。

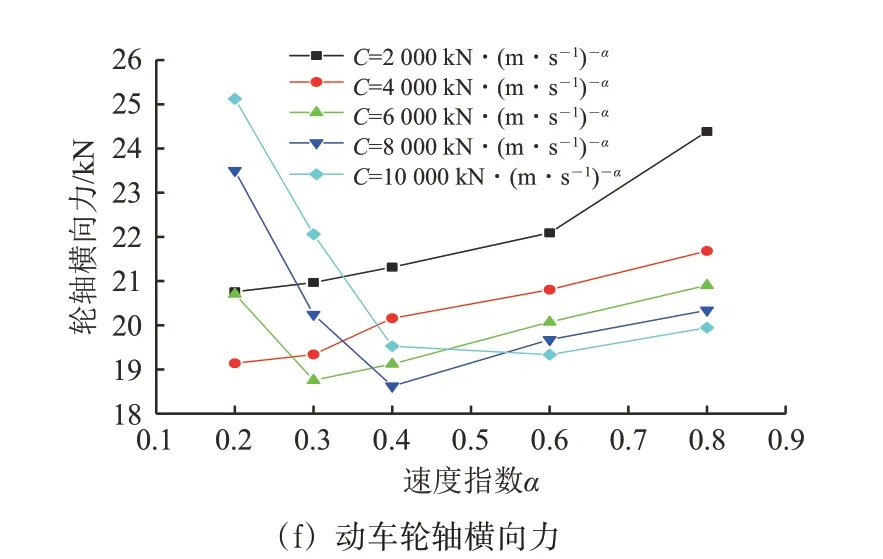
图8 列车动力响应与阻尼器参数的关系
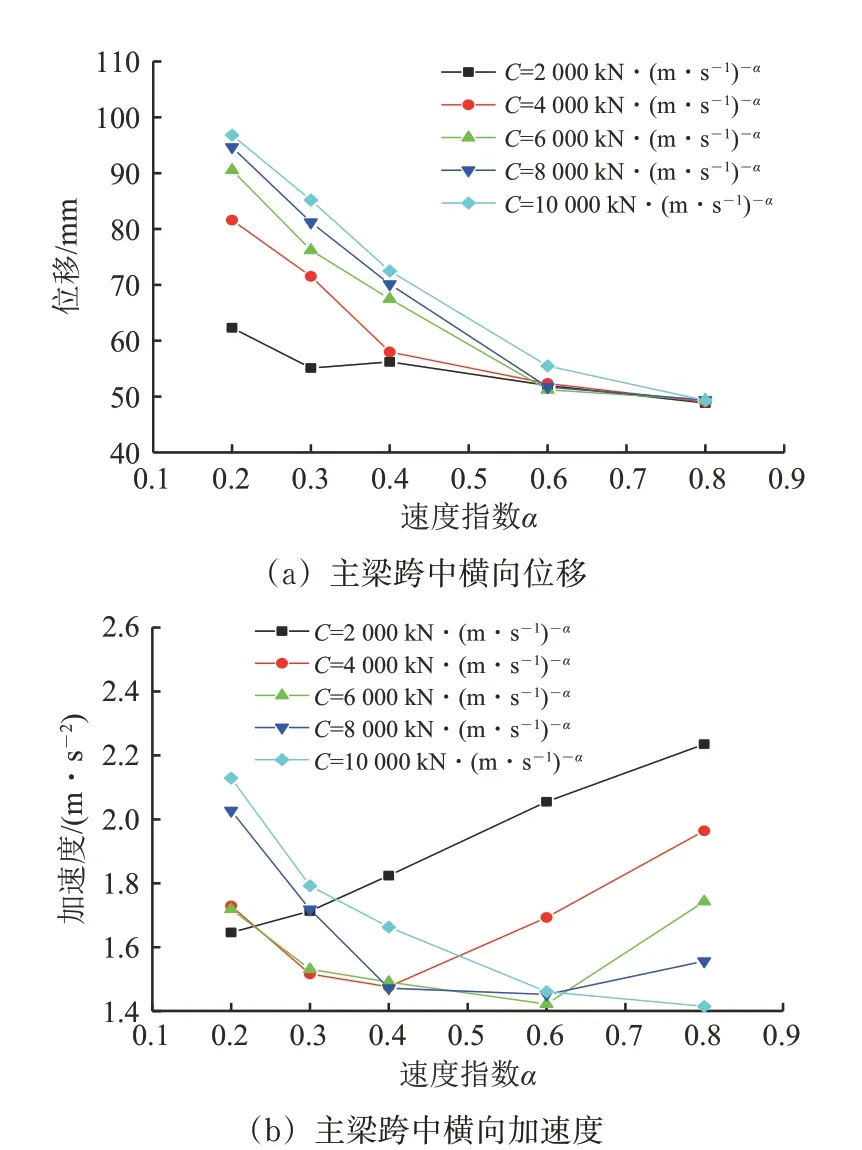
图9 桥梁动力响应与阻尼器参数的关系
与按原设计方案的车桥动力计算结果对比可知:安装横向黏滞阻尼器之后,地震作用下车桥耦合系统的横向动力响应均有明显降低。对于给定的阻尼系数C,拖车的脱轨系数、轮轴横向力大致随速度指数α的增大而减小;动车的脱轨系数、轮轴横向力及动、拖车的轮重减载率当阻尼系数C<4 000 kN·(m·s-1)-α时随速度指数α的增大而增大,而当C≥4 000 kN·(m·s-1)-α时随速度指数α的增大先减小后增大;随着速度指数α的增加,主梁跨中横向位移大致呈减小趋势,当位移降低至60 mm附近时变化不再明显;主梁跨中横向加速度在C处于[4 000,8 000]kN·(m·s-1)-α区间时随着速度指数α的增加先减小后增大,并且在α 处于[0.4,0.6]区间时取得最小值。
对于给定的速度指数α,拖车的脱轨系数、轮轴横向力大致随阻尼系数C的增大而减小;当α<0.4 时,动车的轮重减载率随阻尼系数C的增大而增大,动车的脱轨系数和轮轴横向力随阻尼系数C的增大先减小后增大,并且都在C处于[4 000,8 000]kN·(m·s-1)-α区间时取得最小值;当α>0.4 时,动车的脱轨系数和轮轴横向力随着阻尼系数C的增大而减小;拖车的轮重减载率随阻尼系数C增大的变化规律不明显;随着阻尼系数C的增大,主梁跨中横向位移大致呈增大趋势,跨中横向加速度在α处于[0.3,0.8]区间时先减小后增大。
从参数分析可知,当速度指数α在[0.3,0.6]区间内,列车轮重减载率、动车脱轨系数和轮轴横向力基本达到曲线谷底,且在该区间内C在[4 000,8 000]kN·(m·s-1)-α时取到最小值,拖车及桥梁的动力响应也位于较低水平,因此从减小耦合系统振动响应的角度,阻尼器参数的合理取值为α在[0.3,0.6]区间,C在[4 000,8 000]kN·(m·s-1)-α区间。
为从列车减震效果的角度给出阻尼器的最优设计参数,将针对列车各响应指标(包括动车和拖车的脱轨系数、轮种减载率、轮轴横向力)的减震率平均值最小作为参数优化目的,对于某一响应指标的减震率β定义为
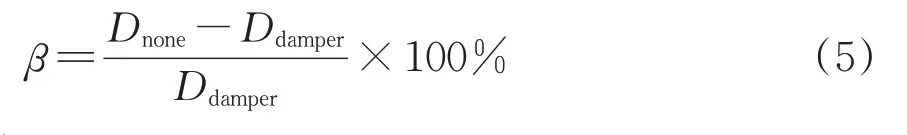
式中:Dnone和Ddamper分别为无横向阻尼器和设置横向阻尼器时系统的地震响应。
基于设置横向阻尼器方案25 个工况的计算数据,求得满足要求的最优参数组合为α取0.6,C取8 000 kN·(m·s-1)-α,此时减震率平均值为38.3%。
5 结 论
(1)随着地震强度的增加,耦合系统动力响应均会增大,地震强度对横向响应的影响大于竖向。
(2)斜拉桥设置横向黏滞阻尼器后,车辆横向动力响应的峰值显著降低,主跨跨中横向位移、横向加速度位移峰值也有所降低。
(3)随着速度指数α的增加,耦合系统各横向动力响应均有明显的变化,所有列车横向动力响应相比普通支座工况均有明显下降,大部分桥梁横向响应相比普通支座工况均有明显下降;随着阻尼系数C的增加,列车横向动力响应相比普通支座工况也均有明显下降。
(4)能起到减小耦合系统振动响应的阻尼器参数取值为[0.3,0.6],C在[4 000,8 000]kN·(m·s-1)-α;耦合系统减震效果最优的阻尼器参数组合为α取0.6,C取8 000 kN·(m·s-1)-α,此时减震率平均值为38.3%。

