考虑施工角度影响的盾构施工地表变形计算方法

赵伯明，王 潇,3，王子珺

（1.北京交通大学 城市地下工程教育部重点实验室,北京 100044；2.北京交通大学 土木建筑工程学院,北京 100044；3.中国建筑股份有限公司,北京 100029）

盾构法是目前城市隧道建设所采用的主要工法，但盾构掘进施工中产生的施工荷载及地层损失会导致地表变形。目前用于盾构隧道施工地表变形的主要计算方法有以下3 种：①经验公式法，Peck等［1-6］基于工程实测数据，提出了采用地层损失率估算地表变形的经验公式，并对地层损失率的取值进行了总结；②理论解析法，SAGASETA［7］提出了“源汇法”，采用弹性力学方法以圆柱体等效替代土体损失，得到了地表三维变形计算式，在该方法的基础上，Loganathan［9］、陈枫［10］、姜忻良［11-12］、丁智［13］和魏纲［14］等相继进行了改进及修正，修正源汇法能够考虑地层空隙的椭圆形非等量径向移动对地表变形的影响；③数值分析法，Lee［15］等开发了1 种三维弹塑性有限元分析技术，能够实现盾构掘进引起地层损失的数值模拟分析及开挖产生地表位移的计算。

实践中发现3 种方法各有所长。经验公式法主要以大量地表沉降监测数据为基础进行回归分析，具有一定的统计意义，但无法体现施工过程中盾构与地层的相互作用，物理意义不明确。理论解析法物理意义较明确、计算简便、且考虑到施工因素的影响，适用于事前对地表变形的预测计算，然而现有方法均假设盾构沿水平线进行掘进，尚未考虑盾构施工角度因素对地表变形的影响效应，其结果必然会一定程度偏离盾构掘进一般呈现一定仰角的施工实际；数值模拟方法能够考虑各种工况及施工因素的影响，但偏于依赖参数选择。

盾构掘进施工角度按方向可分为竖直向倾角以及线路水平转弯引起的水平向倾角，本文主要研究盾构施工竖直向倾角对地表变形的影响。考虑盾构俯仰角和隧道轴线倾角带来的影响，先根据修正源汇法公式和明德林解，推导建立基于施工角度、盾构摩擦力、盾构对地层施加的正面附加推力和同步注浆附加压力、地层损失等施工参数、地层参数的盾构掘进过程地表变形的计算式；再以武汉市轨道交通6号线二期工程金银湖公园站—金银湖停车场站区间盾构施工为背景，针对盾构掘进不同距离时的地表变形，将提出的方法与魏纲方法、累积概率曲线、Peck 公式、数值模拟等既有方法进行对比；最后在验证本文方法有效性基础上，进一步分析不同施工角度对地表变形的影响规律。

1 考虑施工角度的地表变形计算推导

基于修正源汇法公式和明德林解，推导考虑隧道轴线倾角、盾构俯仰角这2 个施工角度影响的盾构施工地表变形计算方法。地层损失通常是盾构施工地表变形的主要因素，实际工程中主要来自开挖面超挖、盾壳的锥形轮廓与盾尾空隙填充不到位。隧道轴线倾角反映了掘进时地层中的地层损失分布，其对地表变形的影响，通过在修正源汇法公式中导入角度参数的形式体现，本文主要针对盾尾空隙填充不到位，具体分析不同隧道轴线倾角下地层损失对地表变形的影响并建立计算方法；盾构俯仰角对地表变形的影响通过在明德林解中导入角度参数的形式体现，因实际施工中盾构掘进通常呈仰角姿态，本文主要针对仰角开展研究。

基于弹性地层假设，建立考虑施工角度的盾构掘进地表变形计算模型如图1所示。图中：OXYZ为以盾构刀盘圆心地面投影点O为原点的坐标系；H为盾构刀盘圆心至地表垂直距离，m；L为直接接触外部土体的盾构外壳长度，m；R为盾构刀盘半径，m；φ为盾构掘进过程中机身轴线与水平轴线的夹角，系施工荷载的作用角度，以正值表示仰角，（°）；λ为隧道设计轴线与水平线的夹角，（°）。

图1 考虑施工角度的盾构掘进地表变形计算模型

盾构施工中，地层损失、盾构与周围土体摩擦力、盾构对地层施加的正面附加推力以及注浆附加压力都会对地层位移与地表变形带来影响，因此在地表变形计算时应考虑以上因素。若假定所有变形均为竖向变形且以向下为正，可定义盾构施工引起地表某点（x,y,0）的变形计算式为

式中：ω为盾构施工引起的地表变形，m；ω1，ω2，ω3和ω4分别为地层损失、盾构摩擦力、盾构对地层施加的正面附加推力和同步注浆附加压力引起的地表某点变形，m。

1.1 基于修正源汇法地层损失引起的地表变形修正计算式

针对地层损失引起的地表变形，参考魏纲等［14］基于源汇法提出的考虑土体泊松比以及采用椭圆形非等量径向土体位移移动模式的Sagaseta 公式进行求解。由于该修正源汇法的假设条件为开挖面与起始位置距离无限远，且隧道轴线倾角水平，其应用坐标系可通过代换与林存刚的明德林解坐标系［16］保持一致，故其解为

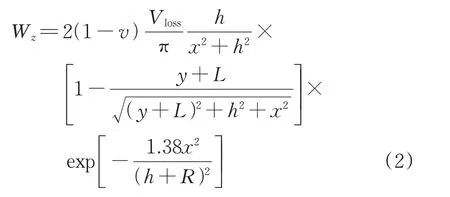
式中：Wz为地层损失引起的地表变形量，m；v为地层泊松比；Vloss为盾构掘进单位引起的地层损失，m3；h为盾构轴线埋深，m。

结合工程实际，通过离散累加方法将隧道轴线倾角引入式（2），推导地表变形修正计算式。

基于修正源汇法假定地层为弹性体，盾构始发后的掘进示意图如图2所示。图中：n为盾构始发后掘进的环数；D为单环管片宽度，m；右向实线箭头表示盾构前进方向。盾构每前进Dm 计算1次，nD即为盾构始发后的掘进长度。设起始状态为：盾构刚完成进洞，尚未安装第1环管片时。

图2 盾构掘进示意图

以掘进至第n环时盾构刀盘中点于地表投影点为原点建立坐标系，掘进单环距离Dm 产生的地表变形Wd为

当隧道掘进轴线为非水平线时，隧道轴线的埋深无法保持一致。基于弹性地层假设，可将盾构以轴线倾角λ掘进至第n环的过程视为以每环为单位、n次掘进的连续累加，即：将盾构始发后每环掘进引起的地表变形Wd的累加，视为盾构掘进至第n环时的地表实际变形。考虑隧道轴线倾角后，盾构掘进过程离散累加模式示意图如图3所示。

图3 考虑隧道轴线倾角后的盾构掘进过程离散累加示意图

为计算盾构掘进至第n环时的地表变形，考虑这一过程中当盾构掘进至第i环处时，刀盘中点埋深hi为

式中：h0为开挖起始点的隧道轴线埋深，m。

设第（i-1）环至第i环开挖面掘进盾尾间隙引起的地层损失为Vlji，可向上取整令向下取整令再计算盾构开挖的起始状态。若设盾构完成开挖第0 环（i=0）时Vlj0=0，则完成第n环掘进（自起始状态掘进长度为nDm）所对应的地表变形Wzjn为

式中：ha和hb分别为盾构掘进至第a环、第b环时的刀盘中点埋深，m。

1.2 基于明德林解施工荷载引起的地表变形修正计算式

针对施工荷载对地表沉降影响的研究，林存刚等根据明德林解［17］的数值积分求得盾构与周围土体摩擦力f、盾构正面附加推力q和注浆附加压力p下的地表变形解［16］。弹性地层内，以集中力作用点于地表投影点O′为原点建立明德林解坐标系O′X′Y′Z′，如图4所示。图中：R1为位移发生点与集中力作用点直线距离，m；R2为位移发生点与集中力作用点在地表以上对称点直线距离，m；Ph和Pv分别为水平和竖向集中力，kPa；G为地层剪切模量，MPa；c为集中力作用点与地表的垂直距离，m。若集中力作用点的坐标为（0,0,c），那么可得到明德林解坐标系内集中力引起点（x′,y′,z′）的水平、竖向变形分别为

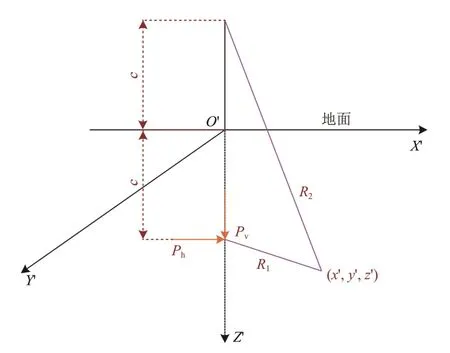
图4 明德林解坐标系示意图

其中，

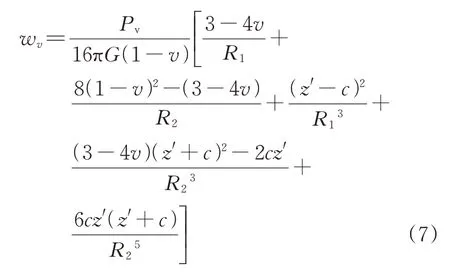
如此，便可通过理论推导，基于明德林解以及盾构掘进过程各施工参数分别建立起式（1）中3种地表变形ω2，ω3和ω4的计算式。

1.2.1 盾构摩擦力引起的地表竖向变形ω2

以积分形式，将摩擦力引起OXYZ坐标系中某点（x,y,0）的竖向变形ω2表示为

式中：ω2h和ω2v分别为摩擦力水平分量和竖向分量引起的地表变形，m。

盾构摩擦力引起地表变形的计算模型如图5所示。图中：dA为盾构机身表面的任意微元体；Θ为刀盘边弧线的圆心角，（°）；dΘ为微元体于刀盘投影弧线的圆心角；s为dA所在位置沿盾构机身至刀盘的距离，m；ds为dA在盾构机身方向的长度。

图5 盾构摩擦力引起地表变形计算模型

微元体摩擦力的分解示意图如图6所示。对于任意微元体dA，都有dA=Rdsdθ，所受集中摩擦力为dP2=fRdsdq，分解为水平分力dP2h=fRcosφdsdθ及竖向分力dP2v=fRsinφdsdθ，此时集中力作用点与地表的垂直距离c=H+ssinφ-Rsinθcosφ。

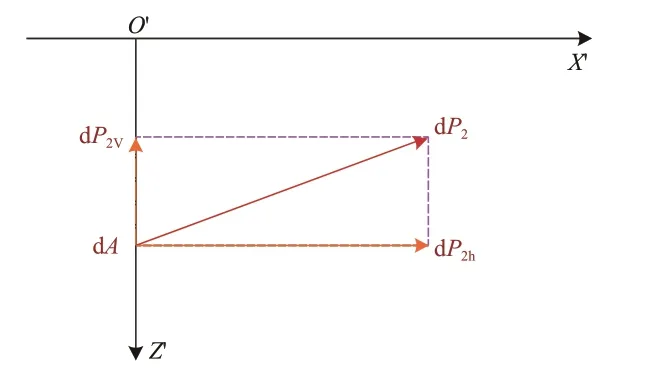
图6 微元体摩擦力分解示意图

将坐标系OXYZ转换为明德林解坐标系O′X′Y′Z′，有

将式（9）代入式（6），可得当z=0 时，摩擦力水平分量引起的地表变形ω2h为

其中，

式中：M1为dA在OXYZ坐标系内与原点O的距离，m。

将式（9）代入式（7），可得当z=0 时，摩擦力竖向分量引起的地表变形ω2v为

1.2.2 盾构对地层正面附加推力引起的地表竖向变形ω3

以积分形式，将盾构对地层施加正面附加推力后引起点（x,y,0）的竖向变形ω3表示为

式中：ω3h和ω3v分别为正面附加推力水平分量、竖向分量引起的地表变形，m。

正面附加推力引起地表变形的计算模型如图7所示。图中：dB为盾构刀盘表面的任意微元体；r为微元体dB距刀盘圆心的距离，m；dr为dB在刀盘半径方向的长度。

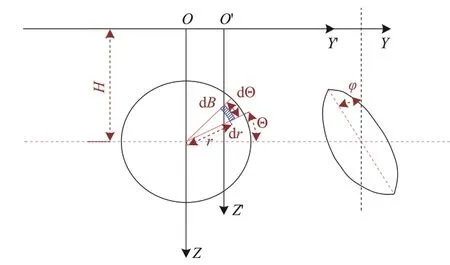
图7 刀盘正面附加推力引起地表变形计算模型

设开挖面上正面附加推力为q，同理对微元体有dB=rdrdq，微元体所受集中力dP3=qrdrdq可分解为水平分力dP3h=qrcosφdrdθ及竖向分力dP3v=qrsinφdrdθ，此时c=H-rsinθcosφ，同前方法转换坐标系，有

可得当z=0 时，盾构对地层施加的正面附加推力水平。竖向分量引起的地表变形分别按式（14）和式（15）计算。

其中，

式中：M2为dB在OXYZ坐标系内与原点O的距离，m。

1.2.3 同步注浆附加压力引起的地表竖向变形ω4

同步注浆附加压力指盾构掘进同步注浆过程中，所注浆液挤压盾尾后方至浆液硬化端周边地层所产生的、垂直于盾构机体轴线的对地层压力。以积分形式，将同步注浆附加压力引起点（x,y,0）的竖向变形ω4表示为

式中：ω4h，ω4vh和ω4vv分别为同步注浆附加压力在X轴水平分量、在Y轴水平分量和在Z轴竖向分量引起的地表竖向变形，m。

假设同步注浆附加压力维持于盾壳后3 m，表现为沿隧道轴线向外的环向力，则其方向及引起地表变形的计算模型如图8所示。其中：dC为盾尾后3 m 浆液与地层接触表面上任意微元体；e为微元体dC在盾构机身方向距离盾尾的距离，m；de为微元体dC在盾构机身方向的长度。

图8 同步注浆附加压力引起地表变形计算模型

当隧道轴线倾角为λ时，对微元体有dC=Rdsdθ，所受集中力dP4=pRdsdθ，垂直距离c=H-Rsinθcosλ。同步注浆附加压力为向地层方向的三维环形力，dP4可分解为沿X轴方向的水平分力dP4h0=pRcosθdedθ，及在YOZ平面内的分力dP4v0=pRsinθdedθ。在YOZ平面内，dP4v0又可进一步分解为沿Y轴的水平分力和沿Z轴的竖向分力，分别为dP4vh=pRsinλsinθdedθ，dP4vv=pRcosλsinθdedθ，同前方法转换坐标系，有

可得当z=0 时，同步注浆附加压力沿X轴和Y轴的水平分量dPh0和dPvh，以及沿Z轴的竖向分量dPvv引起的地表变形分别按式（18）—式（20）计算。

其中，

式中：M3为dC在OXYZ坐标系内与原点O的距离，m。

2 修正计算方法与既有方法对比

为了验证提出修正计算方法的合理性，对比同样施工参数选择下的理论计算、数值模拟等方式计算结果。理论计算时，采用的是Peck 公式和累积概率曲线这2 种基于数据统计并已得到较广应用的地表变形经验计算式以及考虑土体位移模式更为合理的魏纲方法解析式；数值模拟时，分别建立考虑施工时隧道轴线倾角和不考虑倾角（即倾角为0°）的2 种数值模型。以上方法中，魏纲方法、累积概率曲线、PECK 公式仅考虑施工地层损失因素；本文修正计算方法和数值模拟方法则兼顾了施工地层损失、施工荷载及施工角度因素的影响。验证时以武汉地铁6号线金银湖公园站—金银湖停车场站区间为背景，施工参数根据该区间左线左K36+130.968—左K36+190.968里程范围内的设计施工资料确定。

2.1 数值模拟

1）实际工程倾角数值模型

采用有限差分软件FLAC3D，建立实际隧道轴线倾角下盾构掘进数值模型（简称“实际工程倾角数值模型”）。为明确计算条件，假定盾构始终沿轴线掘进，即取俯仰角与隧道轴线倾角相同。结合实际施工条件及相关统计数据［18］，取地层损失率为1.25%。

基于实际工程，确定模型参数为：地层尺寸70 m×60 m×45 m（长×宽×高）；管片宽度1.50 m；单次开挖2 环，共开挖40 环；管片材料为C45钢筋混凝土；盾机长7.50 m，刀盘直径6.48 m，开挖起始处刀盘中点埋深19.00 m；盾壳材料为Q345 钢。实际中隧道轴线倾角3°，因此在数值模型中将水平连续的盾构隧道模型旋转3°，以模拟隧道轴线倾角。

通过FLAC3D中的切向面力设置功能，在盾壳与地层接触环面设置平行于掘进方向的面力以模拟摩擦力，得到的模型如图9所示，地层参数见表1。

图9 数值模型

表1 地层参数

正面土压力采用全土柱计算，盾构掘进起始点地层为黏土，静止侧压力系数为0.36 时，施加的总正面平衡压力为N0=0.36×(2.3×19.3+4.5×19.3+12.2×19.9)=134.65 kPa。

正面附加推力是盾构在刀盘轴线方向施加于地层的超过正面水土压力的部分，大小与千斤顶推力、土仓压力、地层水土压力相关，本例中正面附加推力取30.00 kPa，则模型中施加的总正面平衡压力为N=134.65+30=164.65 kPa。

根据TB 10181—2017《铁路隧道盾构法设计规程》［19］，黏土地层中盾构掘进的摩擦力荷载可取地层黏聚力。因此取施加的摩擦力为40.00 kPa，并取正面附加推力为40.00 kPa。

一般而言，同步注浆压力取1.1～1.2 倍静止水土压力时，便可有效填充盾尾空隙。盾构掘进起始点处土压力按全土柱计算，并取水土压力为222.10 kPa，注浆压力为250.00 kPa，则注浆附加压力为pa=250.00-222.10=27.90 kPa。

为记录地表变形数据并观察变形曲线，取监测区域同数值模拟计算区域，以模型中的计算区域地表中点为原点建立坐标系，开挖方向为Y′′轴，横向为X′轴，开挖面中点对应地表投影坐标为（0,-30,0）。取点（0,0,0）为横断面监测位置1，取点（0,30,0）为横断面监测位置2，监测位置如图10所示。

图10 数值模型监测位置

2）0°倾角数值模型

为了对比未考虑倾角的魏纲方法、累积概率曲线法及Peck 公式，构建不考虑隧道轴线倾角的数值模型（简称“0°倾角数值模型”）并开展计算，如图10所示。除施工角度外，该模型的其他施工参数取值、监测位置均同实际工程倾角数。

图11 0°倾角数值模型

2.2 计算结果对比

盾构掘进至24，48 和60 m 及完全通过后，纵断面、监测位置1处横断面的地表变形曲线分别如图12—图14所示。由图12—图14可得到如下结论。

图12 掘进24 m时地表变形曲线

图13 掘进48 m时地表变形曲线

图14 掘进60 m时地表变形曲线

（1）当掘进至24 m 时，隧道轴线倾角对地表变形的影响尚未显现。由于本文方法与实际工程倾角数值模型不仅考虑了地层损失还考虑了施工荷载影响，因此在盾构刀盘的前方、上方地表出现隆起，这有别于其他方法。

（2）当掘进至48 m 时，纵断面上各计算方法所得曲线在Y′＞15 m 位置重合度较高；本文方法和实际工程倾角数值模型得到的曲线在前半段符合程度较高；监测位置1横断面上，各方法得到的曲线基本重合。

（3）当掘进至60 m 时，纵断面上各方法所得曲线出现较为明显的分离；在横坐标±10 m 范围内，本文方法和实际工程倾角数值模型得到的地表变形明显大于其余三者，且变形曲线呈向下凹陷状，这是由于掘进至60 m 时，隧道轴线倾角对地表变形的影响开始显现；监测位置1横断面上，虽然4种方法的变形曲线形状总体一致，但本文方法、实际工程数值模型得到的地表最大变形显然更大。

当盾构机掘进通过并远离监测区域，地表变形趋于稳定，可将其视为盾构掘进施工完成后的永久变形。根据魏纲方法、累积概率曲线和本文方法3种理论计算方法的结果，当盾构掘进距离达到90 m 时，监测位置1 的地表变形趋于稳定，可设此时为盾构掘进通过状态；对于2 个数值模型，可设盾构脱出地层后的变形完成状态为盾构掘进通过状态。各方法得到的盾构掘进通过后地表变形曲线分别如图15和图16所示。

图15 掘进通过后地表变形曲线

图16 掘进通过后监测位置2处横断面地表变形曲线

由图15和图16可知：不同方法得到的盾构掘进通过后纵断面变形曲线出现较大差异；对于考虑了隧道轴线倾角的本文方法和实际工程倾角数值模型，计算所得纵断面曲线出现明显倾角，而未考虑倾角的其余三者曲线则更接近水平；各方法所得结果的差异随与开挖起始点距离的增大而增加，距开挖起始点越远，倾角带来的影响就显著；在监测位置横断面，如距离起始点60 m处（监测位置2）横断面上，5 种方法得到的变形曲线形状基本相同，但考察各变形曲线中点位置发现，本文方法、实际工程倾角数值模型计算得到的地表最大沉降明显大于其余三者，可见隧道倾角对地表变形的确存在影响，且该影响随掘进距离的增加而愈加显著。

经试算，当掘进90 m 后，监测区域内地表变形趋于稳定。为研究开挖面至变形稳定区域范围内的地表变形，取开挖-30～90 m 范围内对比本文方法和未考虑施工角度因素的魏纲方法与累积概率曲线，得到实际存在施工角度情况下的3种理论计算结果如图17所示。

图17 掘进通过后纵断面地表变形曲线

由图17可知：魏纲方法、累积概率曲线得到的地表变形曲线更为一致，尤其是计算得到变形完成后的最终沉降结果几乎相同；本文方法所得地表变形在头部更高、在尾部更低，这是理论推导时分别考虑到施工荷载挤压地层引起地表隆起，以及隧道轴线向上倾斜时盾构掘进过程加大了开挖对地层影响的缘故；本文方法与这2 种方法所得曲线形态有较大区别，可见施工角度对盾构施工的地表变形存在影响；根据本算例，基于本文方法得到的最大地表沉降出现于开挖面后方约25 m 处，结合理论分析及实际施工经验，这一结果更为合理。

3 施工角度对地表变形的影响规律

3.1 不同施工角度下的地表变形形态

通过上述研究可知，施工角度对盾构施工的地表变形存在影响。为进一步把握这种影响，依据前述方法研究施工角度对地表变形的影响规律。在前例施工参数的基础上，分别计算盾构俯仰角、隧道轴线倾角同取0°，0.75°，1.50°，2.25°和3.00°时，以本文方法计算盾构掘进90 m 后的地表变形，其结果分别如图18所示。

图18 不同施工角度下的地表变形

由图18可知：当盾构掘进至90 m 时，不同施工角度下的隧道上方地表变形均呈中间低、两边高的“V”形，由于本文方法考虑了正面附加推力、摩擦力等施工荷载的影响，在开挖面前方地层表现为轻微隆起；不同施工角度下，地表变形的差别主要体现在隧道轴线上方地表沉降槽中间最低部位；当施工角度为仰角时，自开挖起始处沿着掘进方向的隧道轴线上方地表变形增大，最大位置出现在开挖面后方一定距离处；变形呈现明显的向下凹陷，且当施工角度越大，隧道轴线上方地表变形越大，向下凹陷越明显。

3.2 不同施工角度下的地表变形曲线

进一步分析不同施工角度对地表变形的影响，通过本文方法计算得到当盾构掘进90 m 时的纵断面地表变形曲线及监测位置2 的横断面地表变形曲线，分别如图19和图20所示。

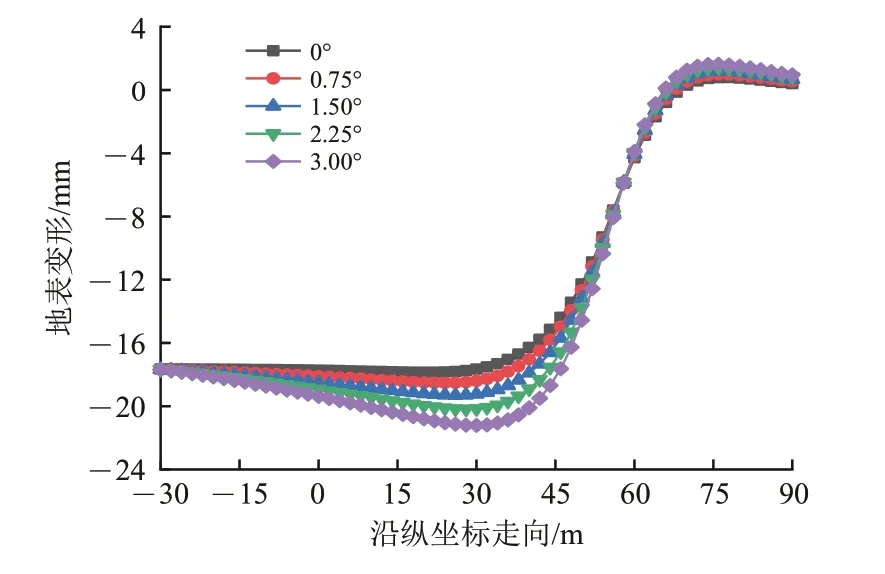
图19 不同施工角度下掘进纵断面地表变形曲线

图20 不同施工角度下掘进监测位置2 处横断面地表变形曲线

由图19可知：当掘进距离为90 m 时，不同施工角度下的地表变形曲线在盾构后方出现明显分离，表现为施工角度越大，开挖面后方纵断面变形越大；在地表自起始点向开挖面呈现沉降值增大趋势，受已开挖地层及前方未开挖地层的共同作用，开挖面后方某点处地表会出现最大沉降，即整个地表的“最低点”；上述变形的主要原因可归纳为，当施工角度增大时，盾构对土体的扰动程度会增加，管片后方的空隙亦会增大，注浆加固的效果产生滞后效应，最终导致地表土体变形增大，并在某点形成最大沉降；按照本文方法，在施工角度为0°和3°的2 种情况下，对同一位置得到的地表变形最大相差约5 mm，这会对实际工程产生较大影响，并且可以预见，在其他施工角度下，隧道最大地表变形也会随着掘进距离的增加而增大。

由图20可得到与图19类似的结论，在监测位置2 处，不同施工角度下的横断面变形曲线也均为两边高、中间低的“V”形，且最大沉降会随着轴线倾角的增大而明显增大。

综上所述，计算得到的盾构于不同施工角度下掘进地表变形形态及地表变形曲线存在较大差异，尤其地表沉降存在较大区别，实际工程中不应忽略施工角度因素对地表变形的影响。

4 结 论

（1）基于修正源汇法公式和明德林解，推导得到的盾构施工地表变形计算方法能够考虑隧道轴线倾角、盾构俯仰角等施工角度因素对地表变形的影响。

（2）基于依托案例对比魏纲方法、累积概率曲线、Peck 公式以及有无角度的2 种数值模型可知，当掘进距离较短时，不同方法计算得到的地表变形重合度较高；随着掘进距离增大，施工角度因素的影响逐渐显现并增大，而本文得到的修正计算方法能够较好地揭示施工角度的影响。

（3）基于依托案例进一步计算，不同施工角度下，地表变形的差别主要体现在隧道轴线上方地表沉降槽中间最低部位；当施工角度为仰角时，自开挖起始处沿掘进方向的隧道轴线上方地表变形增大，最大位置出现在开挖面后方一定距离处。

（4）盾构施工角度对地表变形存在较大影响，不同施工角度下地表变形形态及变形曲线差异较大，实际工程中应注意这一因素对地表变形的影响。