基于改进A＊算法的物流无人机路径优化

张森森，陈 肯，李科扬

（中国民用航空飞行学院空中交通管理学院，广汉 618307）

0 引言

随着经济的发展，人们对物流配送服务的要求越来越高，而物流无人机凭借其不受交通限制、调度方便灵活、速度快等特点，能有效破解物流末端“最后一公里”的难题，很多物流企业顺应潮流发展无人机物流服务，中国民用无人机的发展已经进入了快速增长阶段，因此对于无人机物流路径的研究具有现实意义。文献［4-6］研究了车辆-无人机组合运输问题，以运输固定成本、运营成本和时间窗成本之和为目标函数，构建了基于TSP 的车辆-无人机扩展路径模型，通过一种改进的迭代算法，确定无人机配送路线；文献［7-14］运用函数模拟及栅格法建立环境模型，利用多种改进的A*算法、遗传算法、粒子群等算法仿真无人机三维运行环境下的最优路径；文献［15］提出了一种在侦察区域内通过扫描获取侦察带宽的方法侦察指令，然后结合无人机侦察飞行轨迹计算最短路径原理；文献［16］把各个航路点拆开处理，根据不同航路点分别进行定向搜索，通过仿真实验验证定向进化的可靠性；文献［17］对有禁飞区的区域进行路径规划时，通过建立飞行威胁模型，用双向搜索策略和逆向引导策略解决此类问题。

前人的研究成果主要倾向于无人机的碰撞风险、自主智能避障等方面；对于复杂低空、影响路径规划的因素进行了简化处理，不符合无人机真实运行场景。本文基于栅格法模拟无人机运输三维环境，以路径最优化为目标，利用改进的A*算法与传统A*算法和RRT算法比较分析，探索物流无人机最优路径。

1 环境模型

环境建模的目的是模拟无人机真实运行场景，通过模拟分析研究物流无人机路径优化问题。利用栅格法的建模思想，将无人机运输环境模拟为有很多小方块组成的空间，相当于把三维空间数字化处理，同时令障碍物为1，非障碍物为0。栅格的大小会影响到模拟效果，栅格较小时由于需要存储较多的信息，干扰信号也会随之增加，规划效率和效果随之下降；反之，很少的信息存储量会使得规划效率随之加快，但环境信息划分会变得较为模糊，不利于有效路径的规划。因此，选择合适的栅格大小也是影响规划效果的一个因素。

可以根据无人机运输环境需要进行栅格化二维处理，黑色区域代表障碍物，如图1 所示，把无人机运行环境分成100个小格，并且分别指定好起点和终点。利用三维坐标系建立无人机运输环境，产生以A 点为中心的长方形区域，将其模拟为现实环境，如图2所示。

图1 规划环境二维栅格化示意

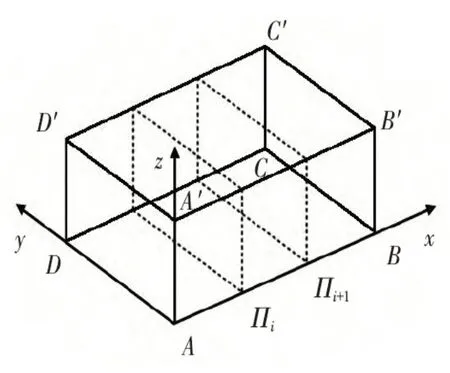
图2 规划环境三维栅格化示意

2 改进A＊算法

2.1 传统A＊算法原理

A*算法考虑将起始点到当前节点的实际路径耗散也作为遴选的条件，表达式为：

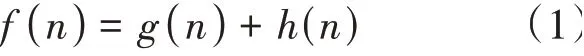
其中，（）为路径规划起始点到中间点所付出的航程代价，（）为中间点到最终点估计的航程代价。

实际代价函数（）表达式为：

其中，、、分别为最小路径长度、最大航程、转弯角和俯仰角，详细叙述见文献［1］：、、为系数，且++= 1。

启发函数h（n）的选取影响A*算法的搜索策略，本文将欧氏距离、曼哈顿距离和others距离三者结合使用，提高启发函数的质量。

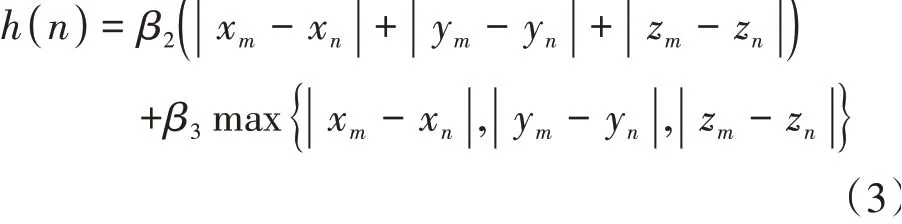
其中，、、分别是欧氏距离、曼哈顿距离others距离的权重系数，且++= 1。

2.2 改进A＊算法

2.2.1 使用hash和堆减少每个栅格的计算量

具体来说，需要使用hash 表备份Open 表，通过优化Open 表，使得所选择的节点带有“可参照性”，而不是单单的直接从Open 表中取。如果Open 表在放入数据之前，我们就让它按照一定顺序，那么从Open 表中取数据时，这些数据就是具备顺序的，是有“可参照性的”。可以选择优先队列的方式。

2.2.2 双向搜索策略

双向搜索相当于有两个起始点，双向去搜索路径，最后相交于同一点。通过正反向搜索相互切换，如此交替往复运行，直到找到一条最优路径。

2.2.3 改进启发函数

动态衡量启发式为：

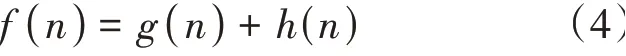
其中（）＞=1。把（）变成了（）*（），在搜索过程中，我们可以通过改变（）来影响（）对A*算法的影响。具体原理是在搜索初始阶段搜索速度较快，搜索末期速度较慢，倾向于搜索最优路径。可以推理出，（）越大，越趋近于BFS 算法；而（）越小，则相对趋近于Dijkstra算法。

2.2.4 路径平滑处理

通过平滑处理可以消除拐点、折角等现象，使飞行路径更加平滑，也更接近于真实飞行方式，可以采用B 样条法对初始路径进行优化处理。

3 算法流程

本文算法流程设计如图3所示。

图3 算法流程设计

步骤1：指定初始点和终点，创建OPEN 集与CLOSED 集，把两点开始放入OPEN集， 经过路径搜索出点并放入CLOSED集。

步骤2：判断是否为最佳路径点，若到达最优点，则把最优点放在CLOSED 集进行进一步的搜索，即执行步骤3，否则执行步骤4。

步骤3：确定搜索是否完成，所得路径即为最优无人机运输路径，否则以当前点为起始继续搜索。

步骤4：以步骤2 中最优节点为中心，向周围进行大范围搜索，不断更新最优点放入OPEN集，继续执行步骤2。

4 仿真分析

比较几种算法的模拟效果，并验证改进算法的优越性，进行仿真实验，指定起始点为（1，2，0），终点为（8，6，2），基础数据见表1。

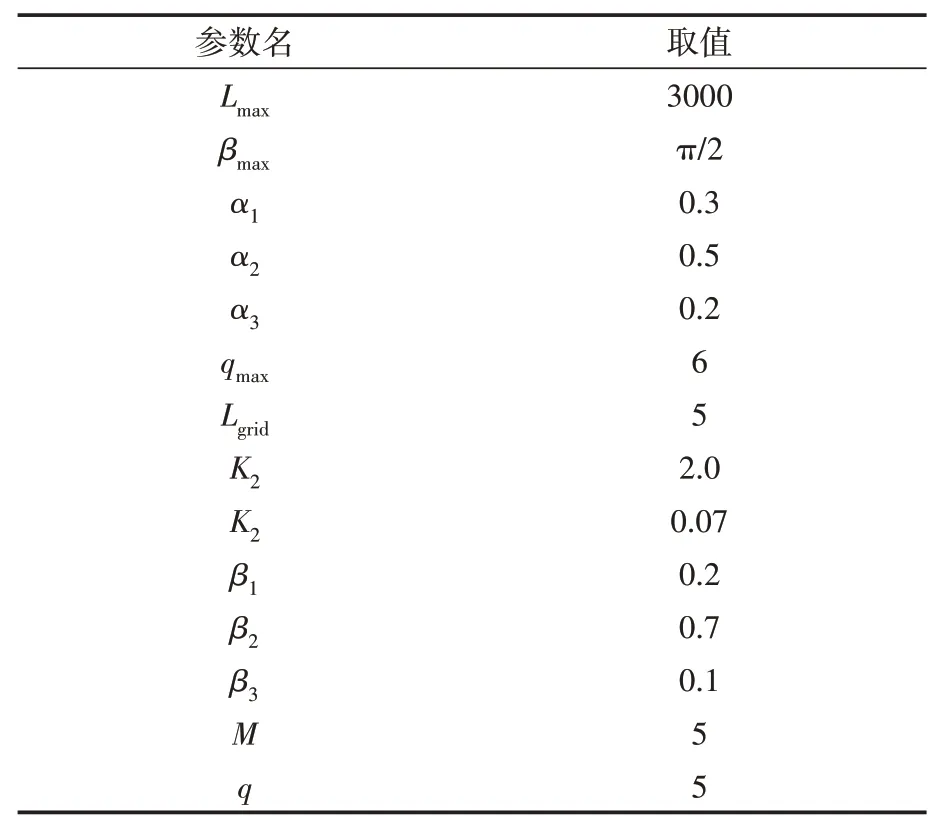
表1 参数取值

利用仿真平台，分别对A*算法以及改进的A*算法进行仿真，结果如图4所示。

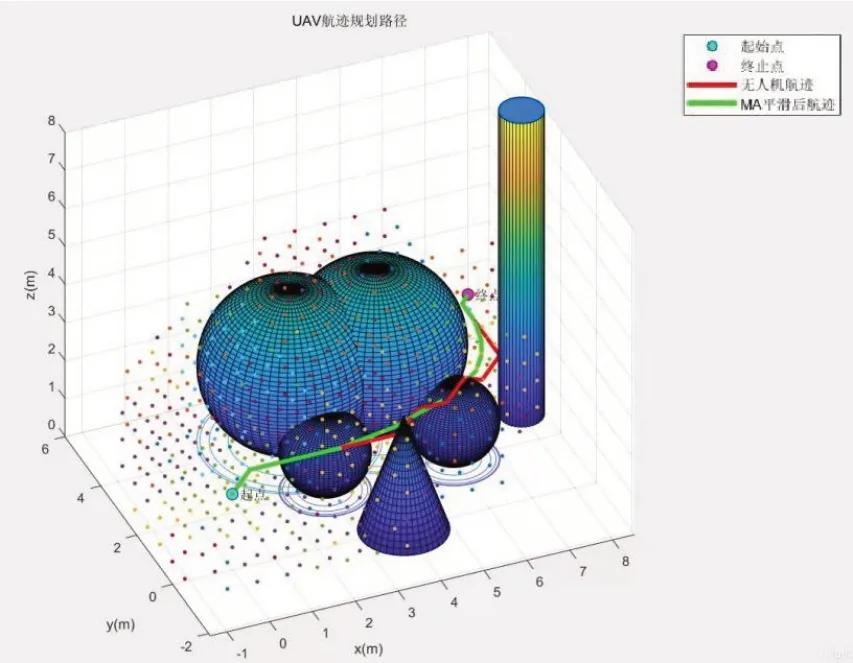
图4 A＊算法和改进A＊算法结果

从图4 可以看出，经过优化处理过的A*算法所计算的路径更短，也更加平滑，符合无人机现实运行情况。因此，本文使用的经过改进的A*算法更加优化了无人机运输路径。

为了增加对比，把RRT 算法的仿真结果也展现出来，如图5所示。

从图5 可以明显看到，此算法所求路径比A*算法要长。三种算法运算数据见表2。

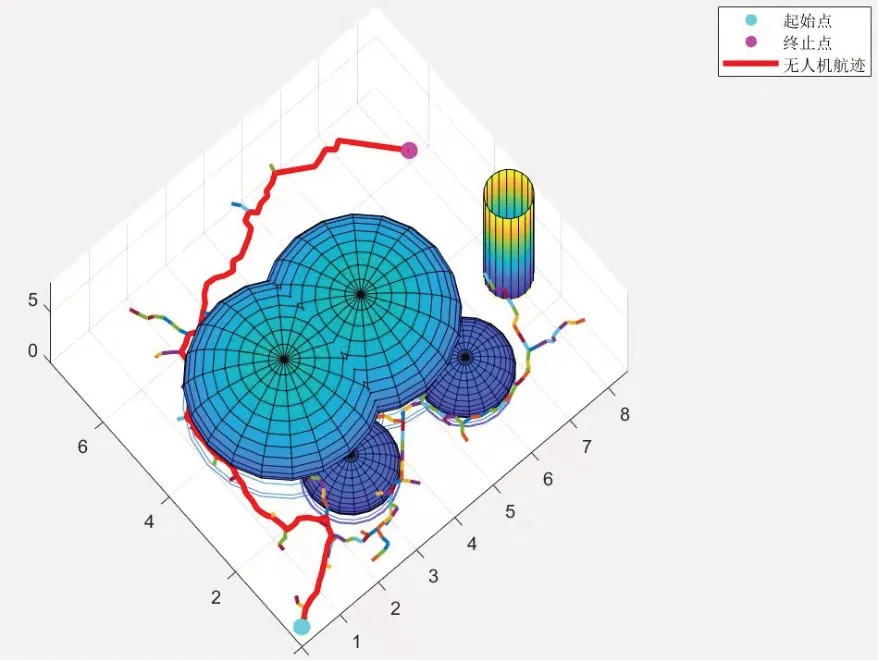
图5 RRT算法结果

表2 几种算法运算数据比较

从计算结果可以看出，A*算法可以更好地靠近最优路径，而RRT 算法迭代时间更短；经过优化的A*算法实现双向搜索之后，搜索效率也明显提升，搜索到的路径更加优化，本文改进的A*算法可以很好地解决物流无人机路径规划问题。

5 结语

本文利用栅格法建立物流无人机三维运行环境，比较分析A*算法和RRT 算法，针对两者存在的缺陷进行双向搜素、启发函数等的改进。改进后的A*算法模拟效果明显更好，而且运行时间更短，模拟出的飞行路径更加平滑，因此，改进后的A*算法能够很好地处理类似问题。