水平管内R1234yf的流动沸腾换热特性

冯龙龙，钟珂，张羽森，商庆春，贾洪伟

（1 东华大学环境科学与工程学院，上海 201620；2 山东电力建设第一工程有限公司，山东 济南 250200）

《基加利修正案》已于2021 年9 月15 日起对中国生效，具有高全球变暖潜能值（GWP）的HFCs 类制冷剂将会被加速淘汰。低温室效应工质R1234yf具有与R134a 相近的热物性，如表1 所示，被认为是一种极具潜力可替代R134a的环保制冷剂。国内外学者也针对R1234yf 和R134a 的换热性能对比及替代应用展开了实验研究。例如，Yang 等和Longo 等通过实验对比了R1234yf 与R134a在4mm管内流动沸腾的换热性能。Yang 等的结果表明R1234yf的换热系数比R134a低约17%；而Longo等发现＜0.3时两种制冷剂的换热系数非常接近，而＞0.3 时R1234yf 的换热系数略低于R134a。Lu 等的实验结果则发现两种制冷剂在3.9mm 铜管内的换热系数差别很小。在应用方面，王锐等的实验研究发现R1234yf 可替代R134a 和R410A，作为喷雾冷却辅助激光手术治疗的替代制冷剂。孟照峰等的实验结果表明混合制冷剂R1234yf/R134a（质量分数89%/11%）可以在汽车空调中直接替代R134a。杨梦等的实验表明R1234yf 与R134a 的混合制冷剂R513A（质量分数56%/44%）可直接用于替代家用冰箱中的R134a，并且其性能要优于R134a。

表1 R1234yf和R134a在饱和温度为17℃时的部分热物性参数

近年来，微细/微小通道因其紧凑的结构、较少的工质充注量、较低的材料成本和优异的换热性能等优点，在R1234yf 的研究中也逐渐受到关注。De Del Col 等对R1234yf 在0.96mm 管内的流动沸腾换热进行了实验，结果表明，换热系数与热流密度强烈相关，而质量流速几乎没有影响。Saitoh 等研究了R1234yf 在2mm 管内的流动换热特性，发现低干度时热流密度对两相换热的影响较大，而高干度时质量流速的影响更显著。Anwar等通过实验研究了R1234yf 在1.6mm 微通道内竖直向上流动的换热特征，结果表明换热系数由热流密度控制，而质量流速和干度几乎不影响换热系数变化趋势。Ribatski 等研究了低GWP 制冷剂[R1234yf、R1234ze(E)、R600a]和R134a 在1.1mm管内流动的沸腾换热，并基于实验测得的3409 个数据点提出了一个新的换热系数预测关联式。

总结前人的研究结果，发现对R1234yf在管径更小（＜1mm）的微细通道内流动沸腾换热特性研究以及该尺度条件下与传统制冷剂的换热性能对比均较为缺乏，因此本文对制冷剂R1234yf 在0.5mm微通道内的流动沸腾换热特性进行了实验研究。实验数据可以扩充R1234yf在微细通道内流动沸腾换热的数据库，主要结论也可为R1234yf的高效应用和推广提供研究基础和实验依据。

1 实验装置

1.1 实验系统

图1为实验系统示意图，主要由储液罐、齿轮泵、质量流量计、预热段、冷凝器以及实验段组成。储液罐用于储存和回收系统中的制冷剂。质量流量（）通过控制齿轮泵的转速和旁通阀门的开度进行调节，并由质量流量计实时测量。预热段为一段外壁面缠绕加热丝的铜管，通过调节单相调压器可控制预热段的加热量，并保证制冷剂在实验段入口处保持一定过冷度（＜3K）。在质量流量计和预热段的前端以及实验段的后端分别装有一个冷凝器（与低温恒温槽连接的板式换热器）用来冷却系统中的制冷剂。测量数据通过安捷伦34972A 记录并存储在电脑中。为了减少系统漏热，所有设备表面覆盖有一层厚度约为9mm、热导率约为0.034 W/(m·K)的保温棉。

图1 实验装置示意图

1.2 实验段介绍

图2 为实验段示意图。实验段为内径0.5mm、外径1.5mm、长度300mm 的不锈钢水平光滑圆管，通过光学3D 表面轮廓仪（SuperView W1）测得管道内表面平均粗糙度约为1.065μm。外管壁上等间距布置11只T形热电偶用于测量外壁面温度，热电偶用聚亚酰胺胶带固定。管道两端焊接有四通结构，并在其垂直方向上分别装有一个铠装热电偶和一个压力传感器，分别用于测量制冷剂在实验段进出口处的温度和压力。实验段两端直接连接一个直流电源（5V，200A），根据焦耳效应（Joule effect）对实验管段进行加热，并通过调节输出电压改变加热量。

图2 实验段及热电偶贴附示意图

2 数据分析

2.1 数据处理及单相实验验证

进行两相沸腾实验之前，需要通过单相流动换热实验测定系统的加热效率（）。由于R1234yf 和R134a 在常压下的沸点较低，为了更接近R1234yf 和R134a 的沸腾实验中实验段外壁面的温度条件，以便更准确地估算有效加热量，单相实验采用了常压沸点较高的R245fa 作为流动工质。为了避免工质在实验段内发生相变，在单相测试过程中应保持实验段温度始终低于制冷剂在对应压力下的饱和温度。由热平衡可知，直流电源输出功率（）等于有效加热量（）与热损失（）之和，如式(1)。

式中，=×，为直流电源的输出功率，W；是工质流过实验段吸收的热量，单相换热仅为显热变化，可写为式(2)。

式中，c是定压比热容，J/(kg·K)；和分别是实验段进出口过冷制冷剂流体的温度。定义为与的比值，如式(3)。

通过上述步骤可获得加热效率，结果如图3所示。可以看到本实验台的平均加热效率约为78.91%。

图3 实验段加热效率

此外，将获得的单相流动换热的Nusselt 数与Gnielinski关联式(4)的预测结果进行比较，如图4所示。可以看到实验测得的单相换热Nusselt 数与预测关联式吻合较好。并且从图4(b)可以看出，97.9%的单相流动数据点都落在±15%的误差范围内，这也表明本文实验装置具有较好的可靠性。

图4 单相Nusselt数与Gnielinski[21]关联式预测值的对比

根据实验获得的加热效率可以估算实验段加热的有效热流密度（），如式(5)。

同时，沿程各热电偶测点对应的内壁面温度（）可通过Fourier定律估算，如式(6)。

式中，为外壁面温度；为实验段管外径；为不锈钢热导率。

于是可获得局部换热系数（），如式(7)。

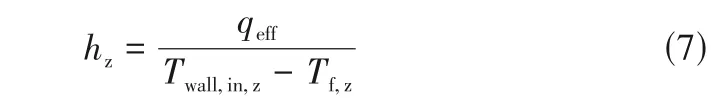
质量流速（）为质量流量与通道截面积的比值，如式(8)。

各热电偶测点处对应的干度（）可通过热平衡计算，如式(9)。

式中，是进口液体制冷剂在进口温度和进口压力下的焓值；是饱和段起始点处的焓值；是制冷剂气化潜热。

上述数据处理过程均由MATLAB 编程实现，计算过程中所需要的制冷剂的热物性参数通过调用物性软件REFPROP 9.1动态数据库直接获得。

2.2 不确定性分析

实验所用的热电偶都经过标准热电偶校准，精度为±0.2K。压力传感器的满量程精度为±0.25%；质量流量计的精度为0.1%；数字电流表和电压表分别用来显示直流电源的输出电流及电压，不确定度均为±0.5%。数据处理过程中涉及的计算参数的不确定度可通过Moffat的方法计算得到，如式(10)。

式中，δ表示参数的绝对不确定度；为自变量；δ为其绝对不确定度。各参数的相对不确定度分别为δ/和δ/。不确定度计算结果如表2所示。

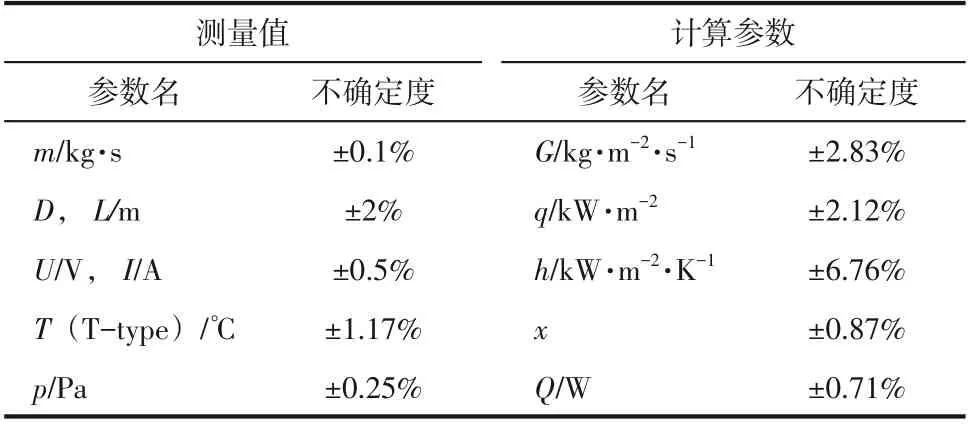
表2 实验参数的不确定度

3 结果与讨论

3.1 热流密度对换热的影响

图5 是R1234yf 在不同热流密度下局部换热系数（）随着沿程干度（）的变化。由图5 可知，在同一干度条件下，均随着热流密度的增大而增大。这是因为随着热流密度的增加，管道内壁面上更多的核化点被激活，气泡数量增多，同时流体扰动也更加剧烈，换热能力得到显著增强。热流密度对两相流动换热具有显著的促进作用，核态沸腾为沸腾换热的主导机制。＜0.7时，的变化趋势基本保持一致，干度对流动换热的影响较小。热流密度较低时，随着干度的增加换热系数略微下降。在低干度区，干度的增大使更多的核化点被激活，管内流型多为泡状流；在中高干度区，随着小气泡的生长和大气泡的合并，管内流型过渡到拉长气泡流。热流密度较高时，换热系数整体呈略微上升的趋势。较高的热流密度使管内成核点在干度较低时就已经被高度激活，换热系数处在较高水平；随着干度的增加，管内流型更早的向拉长气泡流和环状流转变。0.7 时，实验段后端的出现明显的下降，表明管内制冷剂出现干涸。此时管内流型多为弥散流，即制冷剂气体与管道内壁面直接接触，制冷剂液滴以弥散状态分散在管道中心位置，气态制冷剂的导热热阻成为阻碍换热的主要原因。由于热量不能被迅速带走而不断积聚使得壁面过热度迅速增加，导致换热系数显著下降。此外，当热流密度增大时，管内流动的干涸点位置会提前。

图5 热流密度对局部换热系数的影响

3.2 质量流速对换热的影响

图6为R1234yf在=1000～2500kg/(m·s)范围内局部换热系数随着沿程干度的变化。当=50kW/m时，数据点的整体平均换热系数（） 约为6.52kW/(m·K)；当增加到58kW/m时，约为7.45kW/(m·K)。相同热流密度下的局部换热系数基本在同一水平，质量流速对换热的影响较小。当=58kW/m、=1000kg/(m·s)时，实验段后端已经出现换热恶化，而其他质量流速工况还未出现，因此高质量流速能延缓干涸的发生[图6(b)]。

图6 质量流速对局部换热系数的影响

图7 为不同质量流速下R1234yf 的平均换热系数（）随热流密度的变化。由图7可知，在干涸发生之前，沿程平均换热系数均随热流密度的增加而增加，同一热流密度下，不同质量流速的平均换热系数差别很小。R1234yf 的两相流动换热受热流密度的影响较大，而质量流速的影响作用较小。在较高热流密度时，由于靠近实验段出口处出现换热恶化，从而导致平均换热系数随热流密度变化的斜率变小，并且质量流速越大，转折点对应的热流密度越大。这是因为达到干涸所需的热流密度与质量流速成正比，在高质量流速下，壁面热量可以被迅速带走，使壁面温度在较高热流密度时仍保持较低水平。

图7 沿程平均换热系数随热流密度的变化

3.3 R1234yf与R134a的换热特性对比

图8 对比了R1234yf 和R134a 的局部换热系数随干度的变化。可以看出两种制冷剂具有相似的换热趋势。但是由于R1234yf 的汽化潜热比R134a 低约18%，通过相变换热带走相同热量所需的制冷剂蒸发量更多，所以在同一热流密度下，相同测点处R1234yf的干度略大于R134a。此外，由于R1234yf的表面张力比R134a 低约21%，在高热流密度下，R1234yf 的近壁面液膜更易破碎，也更易出现换热恶化。当=58.68kW/m时，R1234yf在测点P-10和P-11处出现换热系数急剧下降，当进一步增加至66.96kW/m时，在测点P-9 处就已出现换热恶化，而R134a在热流密度达到66.96kW/m时仍未出现换热恶化现象。

图8 R1234yf与R134a的局部换热系数对比

图9 对比了R1234yf 和R134a 的平均换热系数（） 随热流密度的变化。在干涸发生前，R1234yf和R134a的分布基本重合，相同热流密度下的差别很小。而随着热流密度进一步升高，两种工质的管内流动均会出现换热恶化，平均换热系数的斜率变小，并且转折点的热流密度均随质量流速的增大而增大，但R1234yf干涸出现时的热流密度显著小于R134a。

图9 R1234yf与R134a的平均换热系数对比

3.4 实验数据与预测模型对比

实验所得的R1234yf 与R134a 的平均换热系数与Cooper和Tran 等提出的核沸腾主导的换热系数预测模型进行了对比，并采用实验数据与关联式预测值的平均绝对误差（MAE）来评估预测模型的准确性，如式(11)。

图10(a)是R1234yf 与R134a 的平均换热系数与Cooper模型的对比结果。两种制冷剂的实验数据与关联式预测值的MAE 分别为10.32%和9.96%。R1234yf 有98.25%的实验值与预测值的偏差可以维持在±30%以内；R134a 有94.74%的实验值与预测值的偏差可以维持在±30%以内。R1234yf 与R134a的平均换热系数与Tran等的模型对比结果如图10(b)所示，两种制冷剂的实验数据与关联式预测值的MAE 分别为5.3%和25.97%。R134a 有70.18%的实验值与预测值的偏差可以维持在±30%以内，而R1234yf的全部实验值与预测值的偏差都在±30%以内。总体来说，两种模型均对R1234yf在微通道内沸腾换热具有较好的预测。

图10 换热系数实验结果与模型计算结果的对比

4 结论

（1）在0.5mm 微通道内，R1234yf 的沸腾换热系数随热流密度的增大而增大，热流密度对两相换热具有显著的促进作用，而质量流速和干度的影响较小，核态沸腾为其主导换热机制。

（2）微尺度条件下，R1234yf 和R134a 呈现相似的换热趋势。相同工况下，两种工质的换热系数几乎一致，但R1234yf出现干涸时的热流密度小于R134a。

（3）实验测得的平均换热系数与Cooper和Tran等的模型预测结果进行对比，发现两种模型都能对R1234yf 进行较为准确的预测，但对于R134a，Cooper模型的预测结果优于Tran等模型。

—— 质量流速，kg/(m·s)

GWP—— 全球变暖潜能值（global worming potential）

HTC—— 换热系数（heat transfer coefficient），kW/(m·K)

—— 换热系数，kW/(m·K)

—— 焓，J/kg

MAE—— 平均绝对误差（mean absolute error），%

—— 质量流量，kg/s

ODP—— 消耗臭氧潜能值（ozone depletion potential）

—— 压力，Pa

—— 热流密度，kW/m

—— 温度，℃

—— 干度

—— 加热效率，%

下角标

ave—— 平均值

exp—— 实验值

l—— 液态

local—— 局部值

pre—— 预测值

sat—— 饱和值

v—— 气态