砾石含水层中质量流失对孔隙渗透率的影响

张天军，李 洋，庞明坤，孟钰凯，张 硕

(1.西安科技大学 安全科学与工程学院，陕西 西安 710054；2.西安科技大学 理学院，陕西 西安 710054)

我国西部矿区煤层覆岩具有浅埋深、薄基岩、厚松散沙层等特有地质条件，采动过程中易受突水溃沙的威胁。为实现突水溃沙风险区的安全开采，专家学者们从西部地质生态环境出发，对突水溃沙的形成机理进行了深入研究，结合现有防治工程，已逐渐形成了突水溃沙灾害防治思路及方法。

针对突水溃沙过程中各类因素存在的影响性问题，学者们分别从流通裂隙、沙粒性质、水力条件等角度开展了研究。伍永平等以泥沙起动理论为基础建立了溃沙伪结构物理力学模型，探讨溃沙发生时沙粒的受力情况，给出溃沙发生条件的理论表达式，但对于溃沙裂隙通道的影响尚未考虑。对此，许延春、陈家瑞和ZHANG等从覆岩裂隙破坏规律和松散层沙粒性质角度出发，开展了裂隙岩石中水沙混合物的流动特性试验，给出了溃沙量与裂隙最大滤沙能力之间的关系，为突水溃沙风险评估提供了参考依据。大量研究表明，含水层内部属性同样是影响突水溃沙的关键因素，基于此，隋旺华等研究了突水溃沙前含水层内部孔隙的水压变化，明确了含水层初始水头和裂缝尺寸是影响水沙涌出量的关键因素，并将孔隙水压力作为突水溃沙预警与监测的重要前兆信息。针对变质量渗透的极限稳定性问题，CHEN和张天军等分别进行了不同黏土含量松散层溃沙的物理试验以及胶结破碎岩体在三轴受压下的渗透试验，将非Darcy流因子作为失稳依据，给出了实现稳态渗透需要满足的参数关系。考虑到水沙在裂隙及破碎岩体中流动的复杂性，杜峰、刘玉、杨鑫等进行了水沙渗透试验，并利用ANSYS Fluent软件对不同因素影响下渗流场的变化规律进行了数值模拟，揭示了水与沙粒之间的相互作用才是影响水沙混合物运动特性的关键因素。

经杜峰、隋旺华等研究发现突水溃沙过程中含水层渗透性变化对于突水溃沙的发生具有重要意义，而现阶段含水层注浆改造作为抑制含水层渗透性技术手段的一种，其防治效果中存在的优化问题仍待研究。为此，笔者在以上研究内容的基础上，针对突水溃沙过程中含水层内部质量流失规律及含水层内部质量流失过程中渗透率敏感因素的问题，利用改进后的变质量破碎岩体渗流试验系统，通过改变初始孔隙度、初始水压梯度、沙粒径等条件，开展变质量渗透试验，研究了砾石含水层沙粒流失状况以及变质量渗透过程中渗透率对于孔隙度的敏感性，以期为含水层注浆改造的效果评估与注浆设计实施过程中参数优化提供参考依据。

1 试验系统及方案

1.1 试验系统

砾石含水层属于典型的多孔介质结构，沙粒作为填充物分布在孔隙之中。当突水通道附近的水力梯度达到或超过含水层中沙粒起动所需的水力梯度，含水层中的沙粒将随水一起流失。

为了对渗透过程中流失质量的数据进行精准采集，笔者设计了一套可以实现破碎岩体变质量渗透的试验测试系统，在改变初始孔隙度、初始水压梯度、沙粒径等条件下，得到沙粒流失对渗透行为的影响规律。

如图1所示，本次试验所用系统主要由DDL600电子万能试验机、渗透仪、高压水泵、计算机数据采集系统及颗粒过滤采集装置等组成，其中渗透仪内包含上、下透水板，颗粒过滤采集装置由盛水容器、过滤筛、电子秤等组成。

图1 变质量渗透试验系统

在进行渗透试验前，先由DDL600电子万能试验机提供轴向位移调节试样初始孔隙度。渗透过程由高压水泵提供试验所需渗透水压并实时采集相应时刻的水压力和流量导入计算机采集系统，承压水由渗透仪上方进入，经上透水板进入试样参与渗透，后经下透水板流出，再由导管流入颗粒过滤采集装置，对试验中流失的沙粒进行收集。

1.2 试验方法

试样骨架选用砂岩，对砂岩进行破碎，按照最大粒径不超过缸筒直径的1/5的标准，依次选取0～5,5～10,10～15,15～20 mm四种粒径区间。填充沙粒按照粒径分别为0.075～0.250(细沙),0.25～0.50(中沙),0.50～0.71 mm(粗沙)。

按照Talbol级配公式，选取幂指数为1，将预先制备的破碎砂岩进行骨架的制配，其中砂岩0.8 kg，沙粒0.2 kg，最后通过搅拌使沙粒能均匀分布于孔隙之中。由于各试样在混合后存在一定的高度差，为方便后期压缩，将压缩前的试样高度均调整为0.11 m。

试样孔隙度通过轴向压缩位移控制法来实现，由孔隙度定义得初始孔隙度为

(1)

式中，为砂岩的密度,2 450 kg/m;为沙粒密度,1 700 kg/m;,分别为试样中砂岩与沙粒的质量；为渗透仪缸筒的内部半径，0.05 m；为压缩后的试样高度。

试验中采用水压梯度表征渗透过程中试样两端水压的变化规律，假定试样两端水压在渗透方向上均匀分布，则水压梯度为

(2)

其中，为试样渗透方向上的位移分量；和分别为渗透仪出、入口端的压力，MPa。试验中渗透出口与大气相通，故=0。

试验过程中利用收集装置获得各个时间段内的沙粒溃出量，待通水后每隔30 s对溃出沙粒收集1次，试验时间均大于180 s，同时记录流量及水压梯度的变化情况。

具体方案如下：

(1)研究初始孔隙度对于沙粒流失与渗透率的影响，压缩位移加载分别为10，15，20，25，30 mm，对应初始孔隙度分别为0.434，0.404，0.372，0.335，0.293，选用含中沙试样。

(2)研究初始水压梯度0对于沙粒流失与渗透率的影响，不同初始孔隙度下，设置3级初始水压梯度4，6，8 MPa/m，经压缩后不同试样高度下根据式(2)进行换算并加载，选用含中沙试样。

(3)研究沙粒径对于沙粒流失的影响，分别选用含细、中、粗沙3种试样，设置初始水压梯度0=6 MPa/m。

1.3 试验原理

在试样渗透过程中，沙粒发生流失(由于试样在压缩过程中难免破碎，故在收集溃出颗粒时本文统称为沙粒)，试样孔隙度发生改变。渗透过程任一时刻试样孔隙度与各时间段内溃出沙粒质量Δ之间存在如下关系：

(3)

因笔者研究重点在于沙粒流失过程中，渗透特征、孔隙度、沙流失量的变化特性，本文中关于渗透率的计算均以Darcy定律下的等效渗透率为依据，以下简称为渗透率。因为试样尺寸较小，重力作用与压力损失相比水压力可以忽略，即

(4)

式中，为水的渗透速度，m/s；为试样渗透率，m；为水的动力黏度，Pa·s。

渗透速度可由流量计算，即

(5)

则试样的渗透率为

(6)

2 试验结果

试验过程中，按照初始孔隙度将试样分为5组，依次编号M-1，M-2，M-3，M-4，M-5。由于破碎岩体试样的变质量渗透属于动态演变过程，其流量、水压梯度、渗透率等参数均具有时变性，故选取渗透过程中的部分特征参量，并以含中沙试样为例，结果见表1。其中，设定水压梯度和流量的变化速率同时大于30%作为突变时刻，变化速率同时小于2%作为稳定时刻，沙粒流失量以180 s时刻为准。

表1 各组试样渗透特征参量

3 试验数据分析

3.1 沙粒流失过程中的渗透参数变化

为了反映不同初始孔隙度下渗透时变特征，以0=6 MPa/m含中沙试样为例,给出了水压梯度与流量的变化情况，如图2所示。

由图2分析可知，试样在不同初始孔隙度下的水压梯度与流量在渗透过程中均出现了数值的突变。随时间的增大水压梯度均趋近于某一水平，各试样之间差距微小，而初始孔隙度对流量变化的影响略有差异，但流量变化总体保持随初始孔隙度的增大而增大。通过对比不同初始孔隙度下突变时刻发现，较大初始孔隙度条件下，突变发生所需的时间缩短，相比于初始孔隙度0.335～0.434，=0.293时突变用时明显延长，说明相同水力条件下，越小，渗透状态越难改变。

图2 不同初始孔隙度下水压梯度及流量变化

通过改变初始水压梯度得到渗透过程中水压梯度与流量的变化情况，以=0.372含中沙试样为例，如图3所示。

由图3可看出，随初始水压梯度的增大，试样水压梯度与流量的突变时刻提前，的下降幅度增大，但最终数值的差异较小。0=4 MPa/m时，试样最终流量的数值基本稳定在10.9 L/min，而6 MPa/m与8 MPa/m时最终流量均稳定在15.8 L/min左右，即随着0的增大，0对于渗透稳定阶段的影响降低。

图3 不同初始水压梯度下水压梯度及流量变化

以上分析表明水压梯度与流量的变化具有良好的一致性，以突变过程为划分依据可将整个渗透过程分为3个阶段。① 缓变阶段：流量和水压梯度均围绕初始值在小幅度范围内缓慢减小；② 突变阶段：流量和水压梯度出现迅速且大幅度的变化；③ 稳定阶段：流量和水压梯度变化到一定数值后基本保持稳定，渗透性质趋于稳定。

3.2 不同粒径下沙粒的质量流失规律

沙粒在含水层内部流失是一个复杂的力学行为，在水流运动下，颗粒除了本身重力、支持力，主要还受到来自水的浮力、曳力、压力梯度力等。为对水流作用下沙粒建立起动模型，在此假设某一含沙的局部裂缝为不随流体流动变化且忽略了曲折闭合的圆形管，如图4所示。

图4 沙粒受力示意

根据力学原理，沙粒的极限平衡状态满足：

(7)

式中，为沙粒直径，m；为滚动摩阻系数，m。

(8)

将沙粒视作标准球形，单个沙粒所受曳力为

(9)

其中，为水的密度，kg/m；为曳力系数。曳力系数为

(10)

式中，为颗粒雷诺数，=。

为避免沙粒粒径大小差异带来的影响，笔者选择体积曳力(即曳力与沙粒体积之比，kN/m)作为标准对沙粒受力进行比较。体积曳力为

(11)

根据试验数据对0=6 MPa/m，=0.372时沙粒的体积曳力计算，得到图5。由式(8)～(11)可知，主要取决于对应时刻的渗透状态及沙粒大小。对比不同沙粒粒径在渗透过程中的体积曳力，按照细、中、粗沙依次减小。在渗透开始阶段，由于沙粒的粒径对于相同压实程度下孔隙结构的影响微乎其微，3种沙粒的体积曳力数值差距较小。随着沙粒的流失，试样的渗透性能发生改变，=30 s时，细沙与中沙试样均经历突变到达稳定状态，分别增大至71 kN/m与28 kN/m，而粗沙试样在30 s后才到达稳定阶段，只有16 kN/m。由此可知，在相同条件下，细沙更易摆脱原有的平衡状态，从而流失。通过对3种粒径沙在不同初始孔隙度下的流失量进行统计，以0=6 MPa/m为例，如图6所示。

图5 体积曳力变化过程

图6 不同初始孔隙度沙粒流失情况

当初始孔隙度较小时，沙粒径变化对流失量影响较小，如=0.293时，沙粒流失量仅为30～60 g，沙粒径的变化对流失量影响较小；而随着初始孔隙度增大，沙粒径变化对流失量影响越大，如=0.434时，沙粒流失量为80～180 g，沙粒径的变化对流失量影响十分明显。沙粒径越小，沙粒流失量对初始孔隙度的敏感度越大。沙粒为细沙时，随着增大，其沙粒流失量呈非线性增长；当沙粒为中沙和粗沙，随着增大，其流失量增长缓慢。

3.3 质量流失对孔隙渗透结构的影响

结合前面的研究结果，渗透过程中沙粒的流失受水压梯度、孔隙度、沙粒径等因素的综合影响，前2种因素属于动态影响。在水流作用下，位于孔隙中的不稳定沙粒随水流失，使得孔隙度增大，水流通道畅通，导致试样渗透性加强，即图7(a)中的状态转换到图7(b)中的状态。

图7 孔隙结构演化

为评估沙粒流失过程中孔隙度的改变，引入孔隙度变化量，可表示为初始孔隙度与初始水压梯度0的函数：

=(,0)

(12)

依照试验含中沙试样所得数据计算，给出试样孔隙度变化统计，见表2。

表2 孔隙度变化量统计

通过数据拟合，0=6 MPa/m时，与初始孔隙度的关系可以用表3中的()表示。=0.372时，与初始水压梯度0的关系则可以用表3中的(0)表示。当0=6 MPa/m，=0.372，()与(0)的数值相等。取0=6 MPa/m，=0.372为基准点，可表示为

表3 孔隙度变化量拟合关系

=(,0)=(0){1+()[()-

()]}

(13)

式中，为特定初始孔隙度，取0.372。

式(13)的推导是以特定初始孔隙度为基准，将0作为参量并考虑初始孔隙度对孔隙度变化量的加成作用，式中同时考虑0与对于孔隙度变化量的影响。图8为孔隙度变化量与初始孔隙率、初始水压梯度0变化关系的拟合曲面。

图8 孔隙度变化量拟合曲面

根据图8所示，试验数据点与拟合曲面能较好吻合。随与0的增大均保持单调递增，越大的区域表示试样在渗透过程中孔隙度调整越大，即流失沙粒越多。同时说明在降低水压力的同时，减小含水层孔隙度，能在一定程度上降低突水溃沙发生风险。

3.4 初始孔隙度对渗透率的敏感性影响

根据达西定律，对试验数据进行计算，可以得到各时刻的渗透率。对比各阶段渗透率的变化情况，缓变阶段试样渗透率相对较小，其数量级为10～10m。随着时间推移，沙粒不断流失，各试样渗透率发生突变迅速增大到10m量级。其中0=6 MPa/m时，=0.434试样的渗透率从最初的3.37×10m增加到5.481×10m，在数值上扩大了16倍，=0.293试样渗透率从最初的6.7×10m增大到2.391×10m，增大了35倍。

为了进一步表征初始孔隙度对渗透率变化的影响，以选定初始水压梯度下=0.434试样的为标准，渗透率随初始孔隙度的平均变化率为

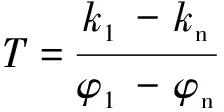
(14)

式中，为试样在选定初始水压梯度下、=0.434时的实时渗透率，m；为试样在同水压梯度下、不同初始孔隙度的实时渗透率，m；为选定的参照初始孔隙度，=0.434；为不同初始孔隙度。

对平均变化率进行无量纲化处理，定义孔隙度敏感系数为

(15)

式中，为孔隙度敏感系数；为同水压梯度下试样=0.434的初始渗透率，m。

图9为三级初始水力梯度下孔隙度敏感系数在渗透过程中的变化曲线。随初始水压梯度0的增大，孔隙度敏感系数的数值范围整体保持下降。以=0.404为例，0=4 MPa/m时曲线的峰值一度达到550，而当0=6，8 MPa/m时曲线的峰值变化至200左右，下降幅度超过60%。结合不同初始孔隙度的值曲线的各个阶段同样可说明在水力条件的加强下，初始孔隙度对于整个渗透过程的影响减弱。

图9 孔隙度敏感系数变化曲线

对于不同初始孔隙度的值变化曲线，其峰值出现时刻皆处于渗透过程的缓变阶段与突变阶段。随的增大，曲线峰值保持增大，且与0任一数值的增大均会使峰值的出现时刻发生提前。当渗透状态处于稳定阶段时，各值变化曲线变化趋势基本相同，数值差距显著减小。说明初始孔隙度对于渗透率的影响在缓变与突变阶段较为明显，而在渗透状态稳定阶段影响的差别较小。

4 结 论

(1)沙粒流失过程中，不同条件下试样的水压梯度与流量由初始值开始缓慢变化，随之发生突变，并最终稳定于某一数值，增大初始孔隙度和初始水压梯度均会降低渗透质稳定性，使突变用时减少。

(2)相同孔隙度以及水力条件下，细沙在渗透过程中的体积曳力明显大于中沙和粗沙。随着初始孔隙度的增大，细沙流失量呈非线性增长，而中沙和粗沙的流失量增长缓慢，即含水层内沙粒越小，发生突水溃沙灾害的可能性越大。

(3)以特定初始孔隙度为基准，根据初始孔隙度与初始水压梯度对孔隙度变化量的影响，给出了孔隙度变化量表达式=(,0)，可作为沙粒流失对于含水层孔隙结构改变的参考指标。

(4)根据孔隙度敏感系数的变化规律分析，初始孔隙度增大对于渗透状态突变起促进作用，且随水力条件减弱，初始孔隙度对于整个渗透过程的影响在增强。由此可知注浆后含水层内孔隙度可以作为注浆效果评估的重要参数，在加强含水层内部填充固结能力基础上配合疏水降压等措施可进一步提升防治效果。