飞机起落架系统摆振动力学研究进展

刘小川，刘冲冲，牟让科

1. 中国飞机强度研究所，西安 710065 2. 结构冲击动力学航空科技重点实验室，西安 710065 3. 陕西省飞行器振动冲击与噪声重点实验室，西安 710065

摘 要：摆振是起落架支柱侧向运动与围绕支柱的扭转运动相互耦合产生的自激振动，对飞机地面滑行的操纵性与安全性等具有很大的危害，是起落架系统设计中重点关注的动力学问题之一。摆振主要有“轮胎型”和“结构型”2类，可以采用动力学理论建模、多体动力学数值分析与全尺寸物理试验等方法对起落架系统的摆振特性进行研究，已发展了线性与非线性理论建模方法和数值工具，建立起了起落架摆振试验系统，也开展了全机瞬态激励下的滑跑稳定性试验。为防止摆振问题的产生，在认识摆振机理的基础上，研究者广泛而又深入地研究了起落架设计参数、轮胎参数、机体特性等对滑跑动响应与稳定性的影响，在获得各种设计参数对起落架摆振稳定性影响的基础上，发展了摆振动力学优化设计方法和智能器件与半主动/主动控制的摆振抑制方法，并开展了试验验证或装机演示验证。结合未来飞机平台的发展和起落架技术的创新，对起落架摆振动力学问题的未来发展方向进行了展望。

飞机滑跑过程中，起落架遭遇外界扰动(不平整跑道、碎石等)作用，机轮将产生一定的偏角，当扰动消失后，如果机轮继续保持周期的或发散的振动，则说明起落架稳定性不足，航空工程中将这类问题称为摆振。摆振是起落架支柱侧向运动与围绕支柱的扭转运动相互耦合产生的自激振动，是飞机地面运动过程中的常见现象和起落架系统的突出动力学问题。

摆振对飞机地面滑行的操纵性与安全性等均具有很大的危害，摆振发生时，起初表现为起落架系统的振动，随着振幅的增大，最终将引起机身的剧烈抖动，轻者使飞行员感觉不适，仪表指针振动，影响其正常操纵，重者可导致机身部件、起落架结构的破坏，严重时可能导致飞机失控冲出跑道等灾难性后果。

飞机机体、起落架系统和机场道面等组成一个复杂的动力学系统，摆振这一不稳定自激振动的能量反馈机制复杂，涉及到间隙、摩擦、阻尼等非线性现象。从摆振现象出发，摆振问题可分为“轮胎型”和“结构型”2类，一般采用动力学理论建模、多体动力学数值分析与全尺寸物理试验等方法对摆振特性进行研究，已发展了线性与非线性理论建模方法与数值工具，通过起落架摆振试验和全机瞬态激励下的滑跑试验，对建立的分析模型和分析方法进行验证。

在深入认识摆振动力学机理的基础上，国内外学者也开展了大量的摆振主、被动控制方法研究，其中采用减摆器是工程中常用的摆振抑制方法，通过合理设计减摆器参数，获得满足摆振抑制要求的动态阻尼，满足起落架在使用速度与载荷范围内的稳定性要求。随着智能材料和控制方法的发展，摆振主动与半主动控制获得了大量关注，特别是基于磁流变液的智能减摆器，因其响应速度快、控制品质好、具有一定被动阻尼效应等优势，其工程样机已通过了起落架摆振试验验证。

本文总结了起落架摆振动力学近年来的研究进展，重点关注了摆振动力学建模技术与起落架防摆设计方法的最新成果，并结合起落架技术和未来飞行器平台创新发展的趋势，总结了起落架摆振动力学应重点关注的问题。

1 摆振典型案例及相关标准规范

近年来国外军民用飞机起落架摆振事故成上升趋势，典型案例见表1，这些事故有些影响了飞机正常操纵，有些导致事故征候或直接造成飞机结构失效。中国的歼6、歼8、运11、运12等飞机也长期受摆振问题的困扰。

表1 典型摆振案例Table 1 Typical shimmy cases

正因为起落架摆振问题的多发性和危害性，国内外飞机研制规范对摆振均做了详细的规定，如表2所示，并要求采取可靠的分析方法或试验方法对起落架的摆振稳定性进行评定。

表2 起落架摆振相关标准规范Table 2 Standards of landing gear shimmy

2 起落架摆振的类型和机理

起落架由上支柱、下支柱、扭力臂、机轮组件等组成，上支柱与机身连接，上支柱与下支柱沿轴向的相对运动压缩缓冲器，吸收地面输入至飞机的冲击能量，机轮组件与下支柱固连，可围绕上支柱轴线旋转运动，实现飞机地面滑跑过程的操纵转向，如图1所示，图中是起落架滑跑航向速度;是机轮偏角;是起落架稳定矩。

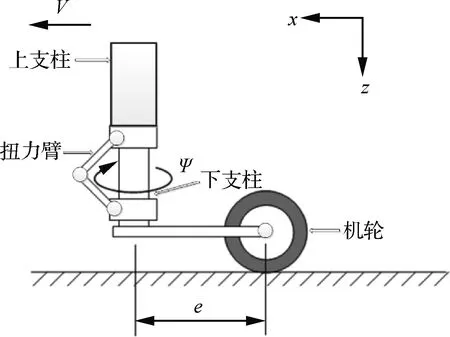
图1 起落架运动关系原理图Fig.1 Motion relationship of landing gear

飞机地面滑跑过程中，地面的支持力是轮胎及支柱变形等起落架运动参数的函数。起落架摆振是起落架支柱侧向振动与机轮围绕支柱轴线扭转振动的耦合振动，与地面不平度、轮胎参数、起落架结构刚度、机体结构刚度等密切相关。一般用机轮绕起落架支柱中心线的偏摆幅度和响应频率来描述起落架摆振特性，据统计，飞机起落架摆振频率范围大约在5～30 Hz左右，而摆振幅度一般都在20°以内。典型起落架摆振机轮偏摆角、角速度dΨd响应曲线见图2。

图2 典型起落架摆振机轮响应曲线[21]Fig.2 Response curves of wheel yaw angle and angular velocity of typical landing gear shimmy[21]

Collins和Black从摆振机理出发将起落架摆振分为“轮胎型”摆振与“结构型”摆振。当减摆器阻尼较小时，起落架在滑跑过程种可能产生一种涉及刚体扭转运动的摆振，即是“轮胎型”摆振，如图3所示，引起“轮胎型”摆振的主要原因是减摆器阻尼及轮胎刚度较小。当减摆器阻尼过大时，轮胎偏航振动变得非常稳定，而起落架支柱的结构振动模式可能变得不稳定，这时机轮摆动角主要由起落架支柱或减摆器传动系统弹性变形提供。这种类型的摆振称为“结构型”摆振。

图3 “轮胎型”摆振Fig.3 Tire-yaw shimmy

周进雄和诸德培认为影响“结构型”摆振的主要轮胎特性参数是轮胎侧向刚度。增大轮胎侧向刚度不利于结构型摆振的防摆；影响“结构型”摆振的关键参数是减摆器传动系统扭转刚度。增大起落架扭转刚度，可显著提高“结构型”摆振的稳定性。发生“结构型”摆振的主要原因是支柱扭转刚度或减摆器传动系统扭转刚度较低或者是两者刚度不匹配。另外，起落架系统存在结构间隙同样会导致摆振，称为“间隙型”摆振。

向锦武和杨冬梅通过灵敏度分析方法，区别研究了“轮胎型”摆振和“结构型”摆振。首先计算稳定矩、支柱侧倾刚度和减摆传动系统扭转刚度等结构参数的改变对减摆器阻尼的影响，以获得速度-灵敏度曲线，然后利用速度-灵敏度曲线分析阻尼特性对摆振稳定区域的影响，灵敏度计算考虑了各参数之间的耦合效应。

3 起落架摆振动力学研究方法

摆振动力学研究方法主要包括线性/非线性摆振动力学理论建模、多体动力学数值仿真、多层级摆振动力学试验等。

3.1 摆振动力学理论建模

3.1.1 线性摆振动力学建模

起落架摆振动力学是典型的运动稳定性问题，根据李雅普诺夫经典理论，在小扰动下，由线性化假定得到的关于稳定性的结论，可以适用于真实的非线性系统，但应考虑足够的裕度。

轮胎是起落架与地面交互的唯一介质，轮胎力学模型和参数对摆振分析结果的准确性有着直接影响，轮胎动力学模型主要有“弦”模型和点接触模型。轮胎“弦”(张线)理论模型原理见图4，是轮胎回正力矩;是轮胎侧向力;是轮胎接触半长;是轮胎侧向变形;是轮胎松弛长度轮胎动特性随运动状态改变，且变化很大，轮胎动力学试验是获得模型参数的主要手段。轮胎刚度随轮胎的滚动状态、滑跑速度、振动频率变化，通过对比不滚动轮胎动力学特性与滚动轮胎动力学特性，两者力学特性相差很大，其中滚动轮胎扭转刚度不到不滚动轮胎扭转刚度的1/3。

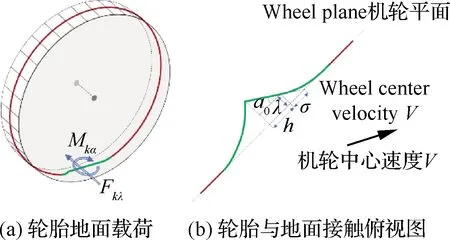
图4 轮胎张线理论模型[37]Fig.4 Stretched string tire model[37]

在20世纪90年代前，已形成了较为系统的摆振问题限定动力学建模理论，以Von Schlippe和Dietrich、Moreland、Collins和Black、Smiley和Pacejka等为代表，轮胎的动力学建模方法的不同是这些方法的主要差别。《飞机前起落架防摆设计要求》要求在建立摆振运动和动力学联立微分方程时，应包括起落架侧向旋转、起落架操纵扭转、机轮扭转、双轮耦合、转向操纵阻尼、机轮运动学方程、轮胎扭转变形、轮胎侧向变形等8个特征方程，其中包括2个独立变量以及机轮扭角、轮胎侧向倾角、机轮相对于飞机前进方向的转向操纵角、转弯操纵减摆器的转弯操纵角、轮迹相对于机轮方向的角位移、轮迹中心的侧向位移等6个自由度。

顾宏斌等采用液压减摆器的流体力学模型代替摆振分析中常用的线性或二次阻尼系数，模型中考虑了油液压缩性的影响采用变化的油液体积弹性模量。Sura和Suryanarayan在考虑摆振速度和摆振频率的情况下，建立了一个三自由度前轮起落架摆振模型，得到了摆振速度和摆振频率的解析表达式，前轮起落架在地面上的最低模态频率近似于摆振频率。Li等建立了包含摆振抑制装置的福克100飞机主起落架的摆振模型，对摆振抑制装置的参数进行了优化设计，应用2种激励方法进行了摆振试验验证，振动峰值降低了16.7%。

刘胜利和刘冲冲等分别建立了考虑起落架与机体连接局部刚度影响的起落架摆振分析模型，轮胎模型分别采用Smiley模型与Moreland模型，采用复特征值优化法对摆振稳定性进行了计算分析，研究表明起落架与机体局部连接刚度对起落架摆振稳定性影响比较明显，局部刚度偏弱可能导致起落架发生摆振。寇明龙等对飞机前起落架在转弯控制状态下进行了摆振分析，应用耗能等效原理建立了主动力和等效黏性阻尼力间的关系，建立并求解以轮胎变形为主的摆振方程组，并根据动态响应的收敛速度确定了防摆所需的主动力及转弯作动器的有效活塞面积。

陈熠等建立了考虑机体动力特性的起落架摆振动力学方程组，研究了机体结构弹性、轮胎刚度对起落架摆振特性的影响规律，发现起落架摆振临界速度、最大临界阻尼值及摆振频率随着轮胎扭转及侧向刚度的增大而增大，而机体弹性使飞机起落架的摆振频率更低，且摆振稳定区变小，更易发生摆振现象。考虑机体弹性飞机摆振响应与刚性飞机摆振响应对比见图5。

图5 考虑机体弹性飞机摆振响应[53]Fig.5 Shimmy response of aircraft shimmy considering fuselage elasticity[53]

周进雄和诸德培研究了起落架稳定距、支柱刚度和减摆器传动系统扭转刚度对摆振的影响，获得了各参数之间的耦合作用。摆振一般发生于飞机前起落架，主起落架动力学设计如果不关注振动匹配问题，同样可能发生摆振现象。Chuban提出了一种基于支柱自由振动频率和振型的主起落架摆振分析方法，考虑了结构的弹性效应，并以典型轻型飞机主起落架摆振分析为例给出了分析过程。

3.1.2 非线性摆振动力学建模

图6 不同轮胎充气压力下起落架双参数分叉图[65]Fig.6 Two parameter bifurcation diagram of landing gear under different tire inflation pressures[65]

Rahmani和Behdinan提出了一种基于非线性摆振振幅图和稳定性边界图的摆振阻尼器性能评估的有效方法，研究了扭矩连杆阻尼器参数和扭转间隙与对摆振的影响，获得了三维摆振图和二维稳定性边界，表明自由间隙会导致低振幅扭转振荡和零稳态侧向振动。Ran等采用能量流法对魔术公式和非恒定松弛长度的轮胎模型进行比较，结果表明非线性轮胎模型不会改变平衡的稳定性，但对振动的幅值有明显影响，为了在大振幅下获得更准确的结果，摆振分析中应包括非恒定松弛长度，如图7所示。Yin等等采用分岔分析方法研究了高速无人机在地面转向过程中方向稳定性，建立了考虑大角度转向运动对交互气动力影响的无人机非线性地面滑行动力学模型，进行了单参数分岔分析，给出了系统的失稳机理，还通过双参数分岔分析研究了主轮距和前轮转向角的影响。

图7 变松弛长度模型[61]Fig.7 Variable relaxation length model[61]

王学军和乔新给出了用以描述五自由度的前轮摆振运动的非线性微分方程组，使用描述函数法研究了扭转间隙、库仑摩擦以及速度平方阻尼3个非线性项对前轮摆振稳定区城的影响。结果表明，非线性项对前轮摆振稳定区域有着重要的影响，由于扭转间隙的存在，使得飞机临界滑跑速度大大降低。陈大伟等根据分岔理论，应用数值延拓算法求解参数化非线性摆振微分方程，得到摆振的 Hopf 分岔点(临界摆振速度)和摆振极限环的幅值，通过李雅普诺夫指数确定极限环的稳定性。

冯飞等建立了双轮共转起落架的摆振非线性动力学模型，并采用分岔计算方法对模型进行了稳定性求解，形成了一套适用于摆振分析的分岔计算方法，对轮间距和双轮共转对摆振稳定性的影响进行了分析，表明轮间距的增加能有效减小侧向摆振的发生区域，对扭转摆振区域则相反，且可能引起摆振区域拓扑结构的改变，双轮共转仅在轮间距较大的情况下，对侧向摆振起到抑制作用。向宗威等总结了国内外现有起落架摆振间隙分析模型，总结了含间隙摆振模型求解方法，说明了不同方法的适用性并，指出其中的局限性及今后建模方向。Cheng等研究了飞机前起落架模型的Hopf-Hopf分岔问题，结果表明，由于高阶项的影响，原始系统的分岔曲线与其截断振幅系统的分岔曲线之间存在偏差，在分岔曲线上可以检测到共振点，当在共振点附近选择垂直力和滑行速度时，会导致轮胎在扭转和侧向方向上产生地面振动。

3.2 多体动力学数值仿真

随着多体动力学仿真方法的发展，刚柔耦合数值分析在起落架动力学仿真中得到了广泛的应用。典型飞机前起落架各构件运动关系见图8。Besselink使用非线性有限元软件MECANO研究了双轮主起落架的摆振稳定性，构建了考虑非线性因素间隙、库伦摩擦和速度平方阻尼的仿真模型，并通过全尺寸试验验证了分析结果的可靠性。

图8 前起落架各构件运动关系Fig.8 Motion relationship of components of nose landing gear

冯飞等通过采用子结构模态综合法将关键部件柔性化，建立了计及前起落架和机身弹性的全机地面滑跑刚柔耦合动力学模型，机身柔性使得飞机中高速情况下所需防摆阻尼平均增加了12.1%。冯飞等根据试验数据对某型飞机进行了地面滑跑虚拟仿真，建立了考虑机身柔性、转向间隙和轮胎参数等非线性因素的刚柔耦合模型，见图9，给出了由滑行速度和临界抗摆振阻尼系数构成的稳定区图。结果表明，轮胎回中力矩系数、松弛长度和前起落架转向间隙对临界阻尼系数有显著影响。杨礼芳在获得轮胎静刚度参数的基础上，考虑到航空轮胎材料非线性、几何非线性、接触非线性等问题，建立了直升机尾起落架全柔性虚拟样机，进行了摆振稳定性分析。

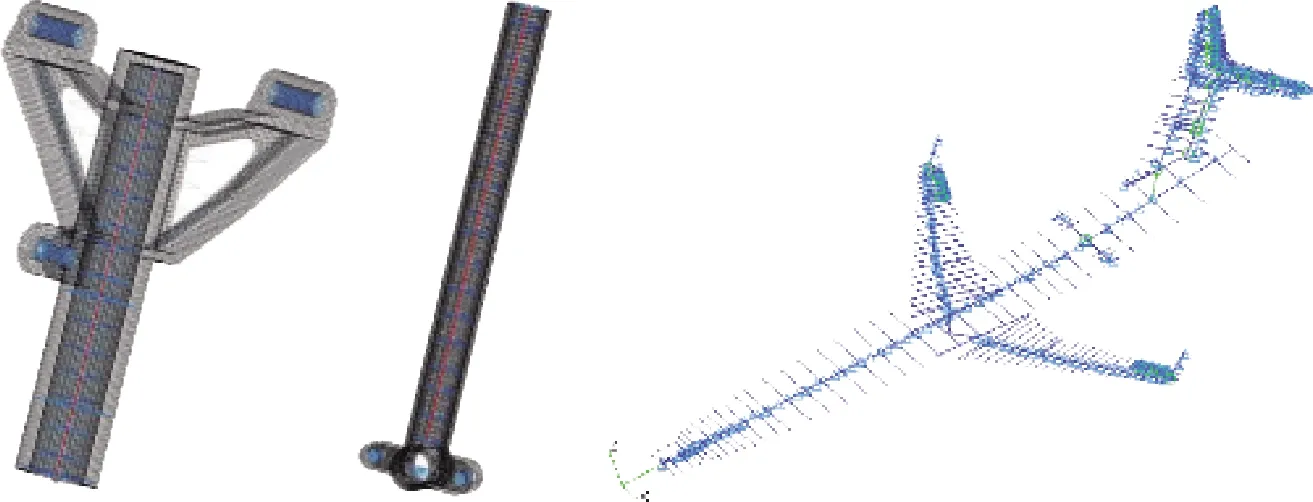
图9 起落架与飞机柔性模型[74]Fig.9 Landing gear and aircraft flexible model[74]

Tartaruga等进行了多体动力学分析和自动分岔分析，考虑了几种起落架和轮胎模型，建立了极限环振荡(摆振)与系统参数变化的关系。德国航空航天中心使用SIMPACK建立了考虑刹车控制系统柔性起落架模型，引入计及侧向动力学效应的轮胎模型，研究了起落架系统的滑行振动问题，评估了刹车走步和摆振等不稳定问题。Beckers等建立了柔性多体起落架模型，研究了摆振Hopf分叉，得到了飞机速度和垂直载荷的分岔图，并开展了摆振阻尼、稳定矩和扭转刚度的摆振敏度分析。Tartaruga等基于奇异值分解的方法，预测了典型飞机前起落架结构的摆振特性，表明分岔方法能够非常准确地预测稳定性边界，并通过敏度分析确定了关键结构参数，量化了不确定性对分岔特性的影响。

Rahmani和Behdinan通过多体动力学仿真，考虑起落架扭转、侧向、航向和轴向自由度以及轮胎、缓冲器和库仑摩擦非线性的影响，研究了前起落架稳定性与关键系统参数的关系，发现库仑摩擦是决定摆振起始和类型的关键因素，并使用非线性灵敏度分析研究了摩擦参数的影响，给出了防摆设计建议。何绪飞等针对民用前起落架系统，建立三维动力学仿真模型，模拟了不同的滑行速度、重量/重心和跑道障碍物，开展刚柔耦合起落架结构的摆振特性分析，评估了起落架减摆阻尼、轮胎松弛长度与侧偏刚度对摆振稳定特性的影响。

3.3 摆振试验

3.3.1 起落架摆振台架试验

起落架摆振动力学试验是验证摆振动力学建模分析方法正确性和起落架摆振设计符合性的可靠手段。《飞机前轮摆振试验要求》规定，起落架摆振试验由减摆器阻尼特性试验、轮胎刚度阻尼试验、起落架系统摆振试验与飞机滑跑验证试验等组成，见图10。通过减摆器阻尼特性试验获得不同频率和振幅下的减摆器阻尼，并发现减摆系统潜在问题，通过轮胎刚度阻尼试验，获得不同轮胎气压下的轮胎刚度及阻尼，为摆振分析提供基础数据。

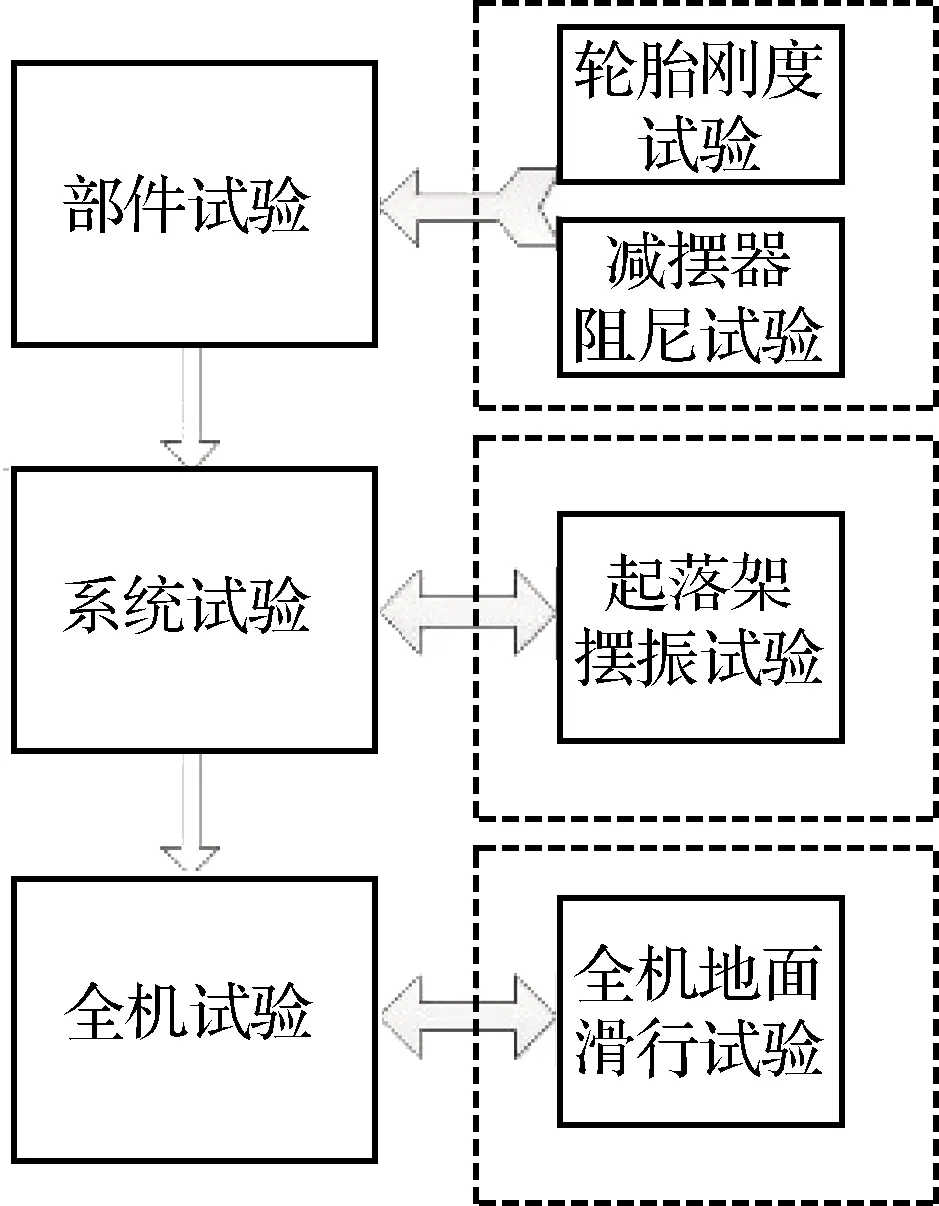
图10 多层级摆振试验验证体系Fig.10 Verification system of multi-level shimmy test

起落架系统摆振台架试验一般在专用的摆振试验台上开展，摆振试验台一般由提升系统、加载框架、飞轮系统等组成，如图11所示。通过飞轮模拟飞机滑跑速度，通过垂向加载模拟飞机重量，通过拉偏角等方式施加初始干扰，模拟验证起落架在地面操纵(起飞和着陆滑行)中受到初始干扰激励后引起的飞机动态响应是否存在不稳定问题。在台架模拟试验中，可以通过局部刚度模拟器与机体动特性模拟器模拟飞机局部刚度及机身动特性对起落架摆振性能的影响。

图11 起落架摆振试验台Fig.11 Landing gear shimmy test bench

早在1956年，美国兰利研究中心就建成了飞机起落架试验设备，中国飞机强度研究所结构冲击动力学航空科技重点实验室也构建了满足200 t级飞机起落架摆振试验要求的摆振试验台。

Krabacher介绍了T-46前起落架摆振参数的测试方法。描述了相关试验测试装置，定义了要测试的参数，描述了数据处理技术，给出了最终计算值，并对起落架扭转自由间隙的测试技术进行了讨论。Black利用模拟跑道的飞轮和模拟机身的起落架安装结构上的实验室摆振测试，说明了实验室测试和飞机滑行测试之间的差异，给出实验室测试和飞机外场滑行对比结果。

Yager在兰利中心的LLT(Landing Loads Track)设备上进行了前起落架摆振测试，试验结果表面混凝土跑道和飞轮摆振试验得到的试验数据十分相似，潮湿跑道和沙土跑道的前起落架稳定性能与干跑道类似。

3.3.2 全机滑跑试验

在飞机全机地面滑行试验阶段，分别进行全机低速、中速、高速及高速抬前轮地面滑行试验，测试起落架及飞机关键部位载荷、位移、速度、加速度、压力等动态响应，验证飞机的滑行稳定性和起落架的摆振稳定性。

贾天娇和汤阿妮开展了起落架地面滑跑试验研究起落架摆振稳定性。通过在跑道上加装激励板，如图12所示，有效激起起落架摆振相关模态；采用模态单峰隔离结合最小二乘算法，通过模态参数识别进行试验数据分析。谢帅等建立了前起落架摆振多体动力学模型，进行摆振工况仿真，识别出工作模态，并从时域和频域2个角度与飞行滑跑试验结果反复对比，不断修改更新模型，完成模型标定，仿真与试验结果对比见图13， 图中:表示起落架关键部位加速度；为重力加速度。最后用模型扩展试验包线，验证了起落架在整个包线范围内的稳定性。贾天娇等还对激励板扭转、侧向、纵向扰动的初始载荷进行了理论分析，包括尺度效应、延迟效应、形状效应，研究了激励板的安装角、横截面形状和尺寸等主要设计参数的影响作用。通过带有柔性体的起落架多体建模仿真方法，分析不同安装角下前起落架扭转、侧向和前后方向的激励效率，以及不同高度和宽度组合设计的激励板激励出的轮胎载荷及轮轴加速度响应。

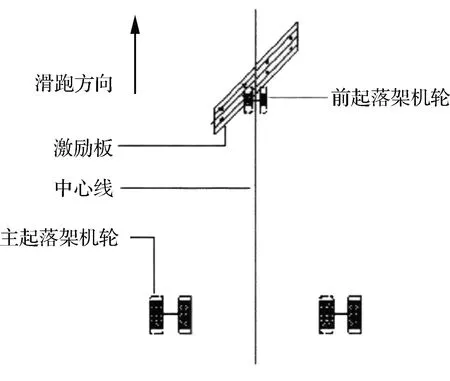
图12 摆振飞行试验激励方法[87]Fig.12 Excitation method of shimmy flight test[87]

图13 飞机地面滑行仿真与试验结果[88]Fig.13 Simulation and test results of aircraft ground taxiing[88]

Grossman开展了F-15飞机地面滑行试验，通过分析与试验结合的方法研究了摆振对轮胎参数值、支柱摩擦系数以及支柱扭转间隙变化的敏感性,评估了设计变更对前起落架摆振的影响。Sura和Suryanarayan分析起落架在地面横向激励的动力学响应，将跑道表面的空间变化转化为功率谱密度的随机地面激励。

某轻型飞机的前起落架在地面滑行过程中观察到了明显的摆振现象，在某些情况下，摆振问题非常严重，成为飞机安全地面操作的障碍。通过实验室摆振试验复现了问题，确定了摆振发生的一些特定条件。通过改进转向轴环，增加转向黏性阻力特性，获得了更大的阻尼和更稳定的摩擦特性，摆振问题最终得到解决。

4 起落架系统防摆振设计方法

工程实践中，主要通过对起落架总体设计参数、减摆器阻尼参数等进行优化设计，以及对起落架振动进行主动/半主动控制等方法，避免起落架在使用条件下发生摆振问题。

4.1 起落架摆振动力学优化设计

常正等阐述了摆振产生的机理和防摆设计中需要重点考虑的因素，结合国内外飞机起落架摆振研究进展，从工程设计角度，提出了起落架摆振分析与验证的思路方法与流程，认为采用减摆器仍是抑制摆振的重要手段，对于保持起落架的稳定性和安全性至关重要。

减摆器一般采用液压式，连接在上支柱与下支柱之间，或在支柱结构上并入扭矩连杆，也可以安装在扭力臂顶点连接处，见图14。另外，还可采用摩擦式减摆器或者安装惯性质量抑制起落架摆振。

图14 不同种类减摆器[66]Fig.14 Different kinds of shimmy dampers[66]

Rahmani和Behdinan介绍了一种新型前起落架摆振减振器的结构拓扑优化设计，见图15，采用一种满足强度要求的扭矩连杆机构抑制摆振，分析结果表明新型减摆机构可以有效降低摆振响应。

图15 扭矩连杆机构减摆器[93]Fig.15 Torque linkage shimmy damper[93]

Liu等利用反向传播(BP)神经网络能，建立了以摆振阻尼孔径、激励频率和激励幅值为输入，以摆振阻尼值为输出的BP神经网络结构软测量模型，利用神经网络对模型进行学习和预测，预测结果证明了方法的可行性和实用性。张海东等在轮胎和起落架结构基本确定的条件下，通过优化减摆器传递比和增加减摆器阻尼提高减摆器减摆能力，调节减摆器相关杆件的长度有效调节传递比，通过增加减摆器活塞面积和缩小阻尼孔油孔面积，增大减摆器阻尼，使改进的减摆器满足新飞机的设计要求。

4.2 摆振的主动与半主动控制

欧盟第七研究框架资助研究了一种电动机驱动的减摆系统，并加入主动控制，通过试验验证减摆器的效能。目前国内外多款中小型飞机已应用电动操纵减摆系统。Tourajizadeh和Zare将滑模控制(SMC)与状态相关方程(SDRE)相结合，设计了一种鲁棒最优控制器，该控制器能有效抑制起落架摆振。为了验证该控制器的最优性能和鲁棒性，利用MATLAB软件对系统的振动响应进行了仿真，并通过对比分析验证了其性能和效率。

陈大伟和顾宏斌采用主动控制策略抑制摆振，建立相应数学模型，应用数值延拓算法求解加入控制后的非线性摆振微分方程。结果表明，适当选取控制参数，在飞机滑跑速度范围内，应用主动控制策略可以达到完全抑制摆振的目的。列举起落架摆振控制研究中采用的控制方法，给出各种控制算法的效果和局限性分析。

Gaétan Pouly提出了2种基于间接模糊自适应理论和直接模糊自适应理论的状态反馈控制方案，并与经典的比例积分微分(PID)方案进行了比较。与PID控制器不同，针对不同测试场景的结果和鲁棒性分析表明，所提出的控制器能够有效地抑制摆振现象。Pouly等在欧洲DREAT项目的支持下，采用模糊自适应控制器进行起落架摆振主动控制。基于李雅普诺夫理论，证明了所提出的自适应控制方案保证了即使估计中出现近似误差，跟踪误差也将渐近收敛到零。仿真结果表明，所提出的控制律产生了真实的控制输入，能够适当地抑制摆振，见图16。

图16 加入主动控制起落架偏摆角响应对比[99]Fig.16 Comparison of yaw angle response of landing gear with active control under random excitation[99]

除了通过飞机转弯控制系统进行摆振主动控制，还可以通过智能材料实施半主动控制。祝世兴等等开展了磁流变减摆器结构设计、磁路设计、控制方法研究、地面摆振试验验证等研究工作，一种磁流变减摆器内部结构见图17。Atabay和Ozkol采用电流相关Bouc-Wen模型建模的磁流变(MR)阻尼器引入有间隙和无间隙的扭转起落架摆振模型。采用遗传算法对Bouc-Wen模型进行参数辨识，并在起落架减摆中应用。Dong等采用线性自抗扰控制技术(LADRC)对摆振进行控制，并与PID控制方法进行了比较。仿真结果表明，LADRC能很好地控制摆振。当飞行速度较高时，稳定时间和幅值均小于PID控制。

图17 一种磁流变减摆器内部结构[104]Fig.17 Internal structure of a magnetorheologic shimmy damper[104]

Kang等基于神经网络中的S型迟滞模型，提出了一种电流闭环和阻尼器活塞杆位移闭环的双闭环控制系统，针对磁流变摆振阻尼器阻尼力输出的强非线性，设计并制作了基于stm32控制器的小型控制电气系统。采用深度神经网络算法设计了多输入单输出的多层训练学习模型。振动频率24 Hz，振幅0.6 mm，不同电流作用下功量图见图18，图中：是阻尼器作用力，是阻尼器振幅。结合摆振试验数据，磁流变摆振阻尼器可以有效地降低起落架在不同工况下的振动，有效地抑制摆振。杨永刚等采用线性二次型(LQR)最优控制策略对由磁流变(MR)阻尼器构成的前起落架减摆器进行半主动控制，考虑其对机轮摆动角度、摆动角速度和侧向位移的影响，对前起落架系统的振动响应和控制性能进行比较分析。仿真结果表明在飞机滑跑速度范围内，半主动线性二次型最优控制作用于磁流变阻尼器中能有效地抑制前起落架摆振。

图18 磁流变减摆器阻尼试验结果[108]Fig.18 Damping test results of MR damper[108]

5 结 语

伴随着飞机发展，起落架摆振问题已有百年的历史，至今仍然是飞机使用过程中的多发性事故征候，军用飞机研制规范和民机适航标准均对飞机的摆振稳定性作了明确规定。从机理出发，摆振问题可分为“轮胎型”和“结构型”2类。一般采用动力学理论建模、数值分析与物理试验手段进行摆振稳定性研究，物理试验方面已形成了涵盖减摆器、轮胎、起落架系统与整机滑跑在内的多层级试验体系。工程中多通过动力学优化方法优化起落架设计参数以在要求的速度-载荷包线内确保起落架的滑跑稳定性，或采用半主动/主动控制手段对摆振响应进行抑制。

起落架摆振是复杂的非线性动力学问题，飞机机体、起落架系统和机场道面等组成一个复杂的动力学系统，摆振这一不稳定自激振动的能量反馈机制复杂，涉及到间隙、摩擦、阻尼等非线性现象，需要对机体结构动特性、起落架设计参数、轮胎参数、道面参数等进行综合匹配设计。随着新能源飞机、高超声速飞机等创新型飞行器的持续涌现，以及电动起落架、复合材料起落架等先进起落架技术的发展，在后续起落架系统摆振动力学研究中，以下几个方面的问题还需要着重考虑：

1) 持续研究湿滑跑道、结冰跑道、晃动舰面、侧风、非对称推力等对摆振稳定性的影响，发展更高精度的轮胎模型，进一步完善摆振稳定性的非线性随机动力学建模方法与求解方法。

2) 关注电驱动起落架、复合材料起落架、磁流变充填起落架等先进起落架的摆振稳定性问题。

3) 通过智能作动器件和半主动/主动控制方法，综合考虑起落架滑跑稳定性与滑跑动响应问题，在保持稳定性的同时，降低传递至机体的动态载荷，并提高滑行舒适性。

4) 随着数字技术的发展，探索数字孪生在起落架滑跑动力学领域的应用，构建起落架数字孪生模型，通过振动响应在线监测，开展数据驱动的摆振稳定性预测等研究。