白砂糖与赤砂糖联产的煮糖制度经济效益分析
黄振军,钟志才,李朝明,黄文华,曾练强*
(1云南西双版纳英茂糖业有限公司,云南 景洪 666100;2广东省科学院生物与医学工程研究所,广东 广州 510316;3云南西双版纳英茂糖业有限公司勐阿糖厂,云南 景洪 666100)
0 前言
我国甘蔗糖厂在生产普通一级白砂糖时最常用的煮糖制度是三系煮糖制度。但在榨季初期糖浆纯度低时,可以用二系或二系半煮糖制度;榨季后期糖浆纯度高时可以用三系半或四系煮糖制度。煮糖制度就是规定各系糖膏和糖蜜等中间制品的纯度,以及各种物料的使用流程,即煮制各种糖膏和种子所用的物料[1]。
如何制定合理的煮糖制度是制糖生产的重要环节,其中丙糖(又称赤砂糖)的处理方法直接影响白砂糖的质量和煮炼回收率,并影响糖厂的经济效益。目前常用的几种方法都有不妥之处:
(1)赤砂糖回溶,经过处理后用于煮甲糖。这样会加大物料处理量,增加能耗;处理过程造成蔗糖的转化损失;而且处理效果不好时,对白砂糖质量有较大的不良影响。
(2)赤砂糖作为乙糖种子进行套种处理。在赤砂糖色值较低时,这种方法有较大优点。但如果赤砂糖质量不好,例如色值高、晶粒不均匀,则会影响乙糖质量,并最终影响白砂糖质量,严重时会使白砂糖带有色泽较深的内核,成为“夹心糖”。这种方法只能用于煮制晶粒较细的白砂糖,不能煮粗粒糖(否则色泽不好)。
(3)将赤砂糖回溶糖浆与混合汁一起再过澄清处理,但流程长,糖分损失大,而且提高了蔗汁锤度会给澄清带来一定的影响。
(4)将赤砂糖加入乙糖蜜混合成糖糊再复筛,减少它表面所带的废蜜,但由于赤砂糖晶粒细(特别是使用连续分蜜机以后),效果不好。
将部分赤砂糖直接作为产品销售,这种白砂糖和赤砂糖联产的煮糖制度,使生产流程更加简单,白砂糖质量提升,且糖分回收率较高[2],减少回煮量有利于节能减排。但由于目前赤砂糖在国内不是主流产品,也尚未形成稳定的需求,销售价和销售量均不稳定。因此,有必要进行经济效益分析,以帮助企业面对变幻莫测的市场进行决策。
本文用敏感性分析方法[3],在制定白砂糖和赤砂糖联产的煮糖制度时,对产生影响糖厂收入的主要不确定因素进行分析,预测可能的风险,为企业决策提供依据。
1 敏感性分析
敏感性分析是针对潜在的风险性,研究项目的各种不确定因素变化至一定幅度时,计算其主要经济指标变化率及敏感程度的一种方法。敏感性分析是在确定性分析的基础上,进一步分析不确定性因素对项目最终效果指标的影响及影响程度。本项目中考虑甘蔗糖厂的主要产品为白砂糖、赤砂糖、糖蜜等,销售收入也主要受这些产品的产量和单价影响,计算公式如下:

其中:G为产品销售总额(元);
ms、m、mm分别为白砂糖、赤砂糖、糖蜜的产量(t);
Ps、Pb、Pm分别为白砂糖、赤砂糖、糖蜜的单价(元/t)。
而根据王鞠萱[4]推导的公式,当赤砂糖部分打包时,白砂糖与糖蜜的产量与赤砂糖打包量m的关系如下:

其中:J、M、S、Sc分别为糖浆、糖蜜、白砂糖、赤砂糖的简纯度(%);mJ为糖浆的量(t)。
则式(1)可换算为:

1.1 不确定因素
在式(4)中,A、B、C、D由J、M、S、Sc、mJ计算所得,与市场价格变化无关,在此作为常量处理。当白砂糖和赤砂糖联产时,根据Ps、Pb、Pm随市场的变化而制定赤砂糖打包量m,以期达到较好的经济效益,因此Ps、Pb、Pm、m为不确定因素。
1.2 单因素分析
令J=85%,M=40%,S=99.8%,Sc=88%,mJ=100 t来作假设计算。则A=75.25,B=0.8026,C=24.75,D=0.1973。
代入式(4)计算:
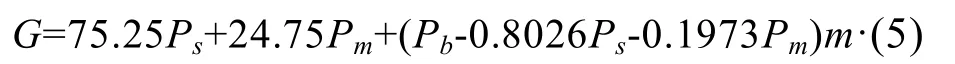
1.2.1 敏感系数
敏感系数是指分析指标变化的百分率与不确定因素变化的百分率之比。基本方案为:Ps=5800元/t,Pb=4800元/t,Pm=1600元/t,m=6 t,此时G=475025元。
敏感系数E=(ΔG/G)/(ΔK/K),其中K为不确定因素。
敏感系数计算示例:
求不确定因素m的敏感系数E(m):
m增加10%,则G=474922;m减少10%,则G=475127。
则ΔG/G=(474922-475127)/475025=-0.000431;
ΔK/K=[m(1+10%)-m(1-10%)]/m=20%;
因此E(m)=(ΔG/G)/(ΔK/K)=-0.00216。
其余以此类推,单因素敏感系数计算结果如表1所示。

表1 单因素敏感系数计算表
表1计算敏感系数时,与基本方案的假设有关。如果Pb-0.8026Ps-0.1973Pm≥0,打包量m的敏感系数是正数,说明打包越多越好;若Pb-0.8026Ps-0.1973Pm<0,打包量m的敏感系数是负数,说明打包越多越不好。本例中基本方案假设的情况下,打包量和敏感系数为-0.00216,说明打包越多,经济效益越差。
1.2.2 敏感性分析图
敏感性分析图见图1,纵坐标表示总收入,横坐标表示单因素分析指标变化的百分率,斜率绝对值越大,说明越敏感,正数为正相关,负数为负相关。
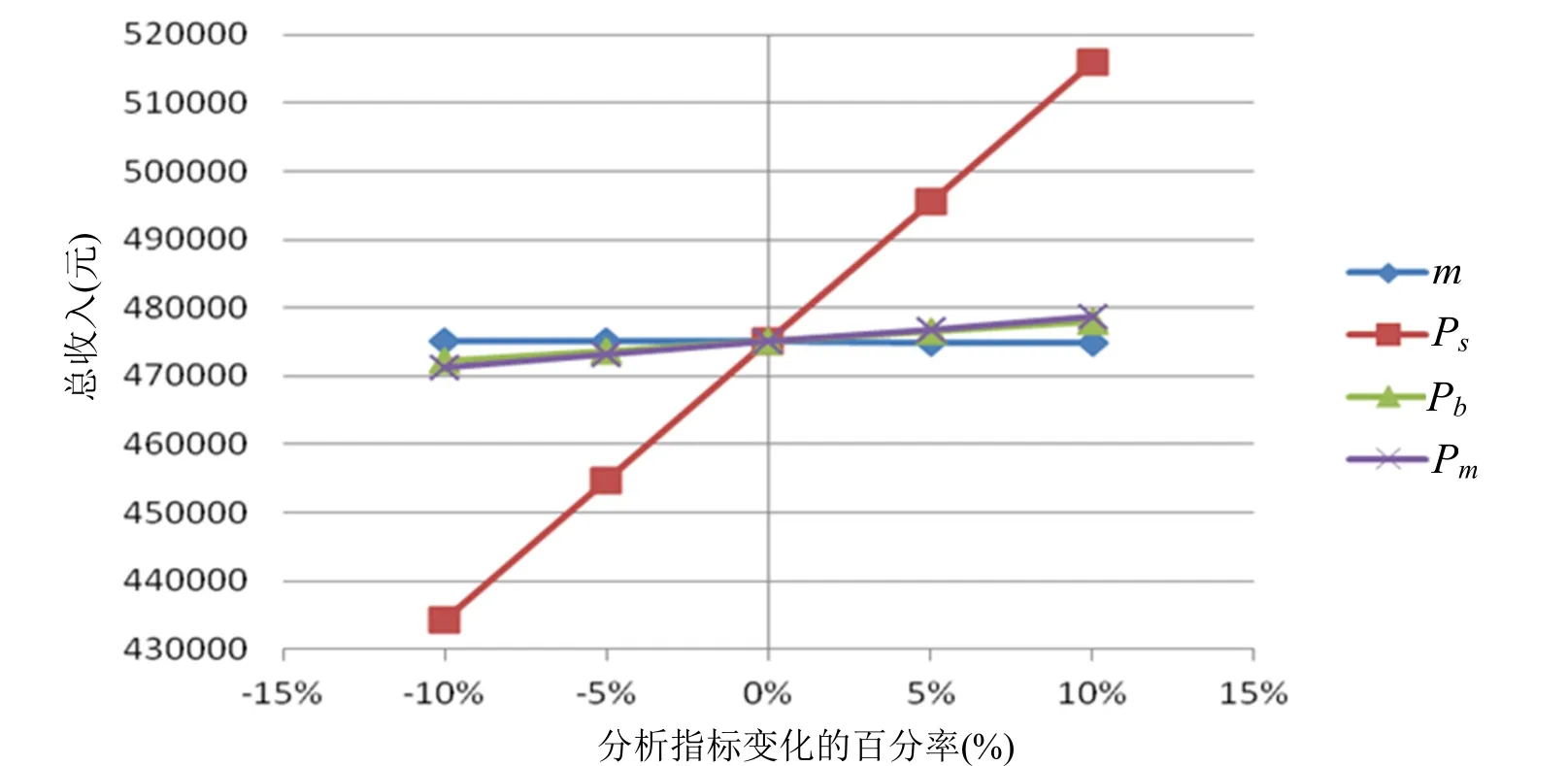
图1 敏感性分析图
2 敏感性分析结果解析
2.1 影响糖厂收入的主要因素
从表1可见,赤砂糖打包量、白砂糖单价、赤砂糖单价、糖蜜单价引起的敏感系数分别为-0.00216、0.860、0.0606、0.0794,白砂糖单价对糖厂收入起决定性的作用,其他因素的影响较小。原因是在于本方案中白砂糖的产量占据了绝大多数,赤砂糖打包量不到白砂糖产量的5%,糖蜜的量也只有白砂糖的产量的16.7%,而且糖蜜纯度只有40%。
2.2 赤砂糖打包量的决策
从式(4)可以看出,当Pb-0.8026Ps-0.1973Pm≥0时,m越大,G也越大;反之当Pb-0.8026Ps-0.1973Pm<0时,m越大,则G越小。即当赤砂糖单价高于0.8026倍白砂糖单价与0.1973倍糖蜜单价之和时,赤砂糖打包量越大越有利于糖厂经济效益;反之当赤砂糖单价低于0.8026倍白砂糖单价与0.1973倍糖蜜单价之和时,赤砂糖打包量越小越有利于糖厂经济效益,但由于赤砂糖打包有利于白砂糖产品质量的提高,因此应综合考虑。
3 应用实例
假设糖浆简纯度为85%,最终糖蜜简纯度为40%,100 t糖浆,经过精确计算白砂糖与赤砂糖联产的三系煮糖制度如图2、图3所示,赤砂糖打包量为0时,白砂糖产量为75.25 t,糖蜜产量为24.75 t;赤砂糖打包量为6 t时,白砂糖产量为70.44 t,糖蜜产量为23.56 t。
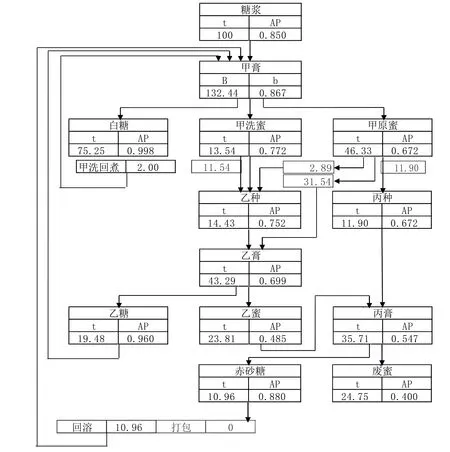
图2 赤砂糖打包量为0的三系煮糖制度
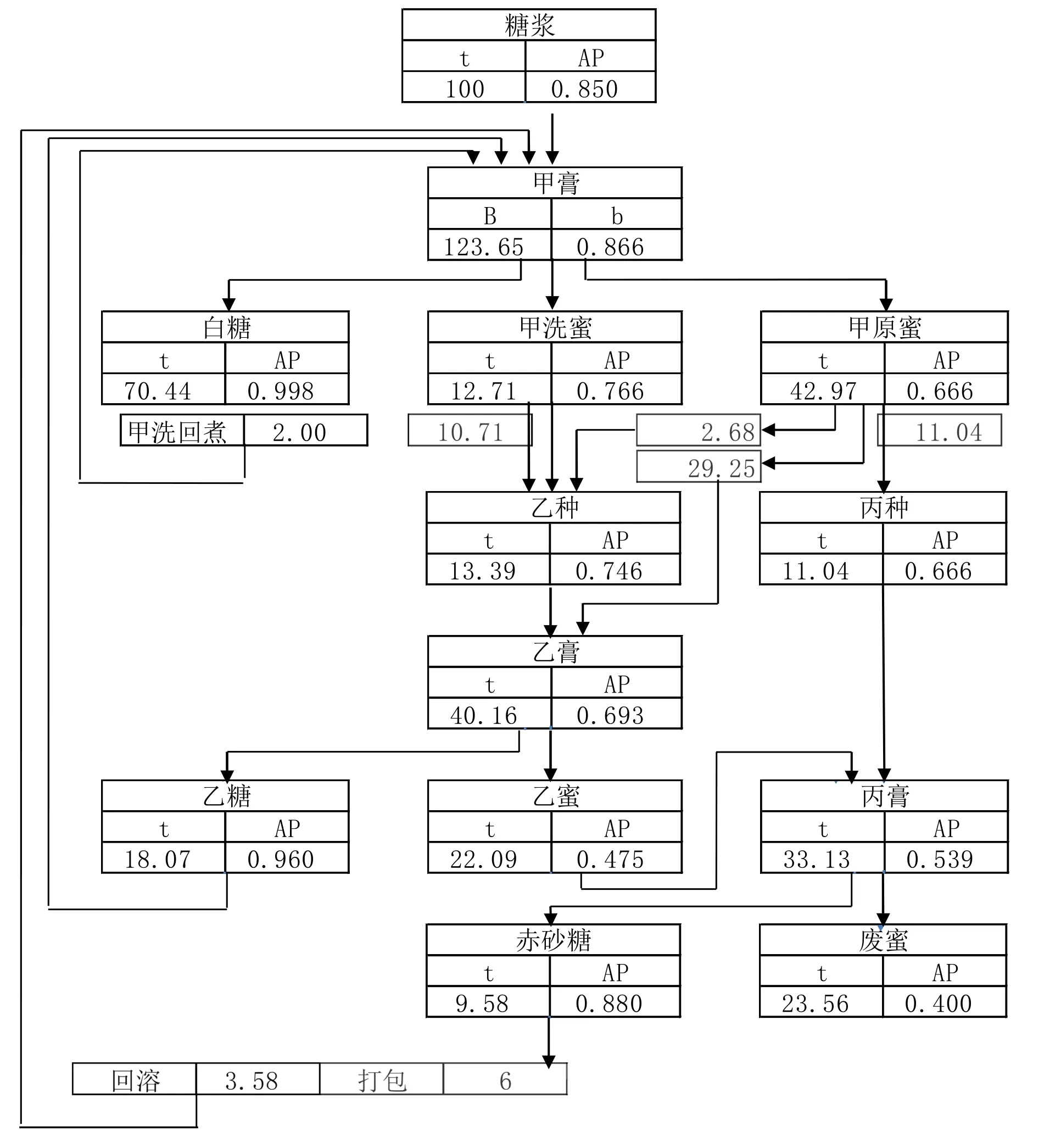
图3 赤砂糖打包量为6 t的三系煮糖制度
根据上述分析,如果Pb-0.8026Ps-0.1973Pm>0,打包越多,经济效益越好;反之,若Pb-0.8026Ps-0.1973Pm<0,打包越多,经济效益越差。
按当前市场价Ps=5800元/t,当Pb=4800元/t,Pm=1600元/t计,Pb-0.8026Ps-0.1973Pm=-268.2<0,从经济效益角度考虑,不建议赤砂糖打包。
根据上述公式(5),即G=75.25Ps+24.75Pm+ (Pb-0.8026Ps-0.1973Pm)m计算:打包量m=0时,总产值为=476053.5元;打包量m=6 t时,总产值为475026.1元。
同时,从煮糖制度图中也可根据公式(1),即G=msPs+mPb+mmPm计算总产值。
赤砂糖打包为0时,G=75.25×5800+24.75×1600 =476050元;赤砂糖打包6 t时,G=70.44×5800+ 6×4800+23.56×1600=475048元。
2种方法计算结果基本相同,误差可能是由于计算时所取的有效位数引起。
4 结果与讨论
在制定白砂糖和赤砂糖联产的煮糖制度时,敏感性分析方法可根据市场价格变化预测经济效益,当Pb-BPs-DPm>0时,可增加赤砂糖打包量,反之则建议赤砂糖不打包。
当然,我们也要考虑赤砂糖打包出售的煮糖制度工艺,除了经济效益之外的其他因素,比如说赤砂糖打包后无需循环处理,可以减少煮制糖膏的总量(见表2),并减少了煮糖过程的非糖杂质恶性循环和蔗糖转化的损失,对产品质量提升,节约能耗和提高日榨量等都有良好的作用。

表2 赤砂糖打包量对糖膏煮制量的影响

