数学建模案例融入线性代数教学的探索

李燕娟 王芬琴

兰州博文科技学院 甘肃兰州 730101

1 概述

线性代数课程是理工类专业必修的一门专业基础课，它在工程技术等领域有着广泛的应用，并且在培养学生逻辑思维能力方面起着非常重要的作用。但是线性代数教学目前仍然存在以下问题：第一，着重理论教学，晦涩难懂，导致学生学习主动性不强；第二，与实际问题联系较少，不利于学生数学应用能力的培养。因此，线性代数教学改革迫在眉睫。

数学建模是根据实际问题用数学语言转换为数学问题，进而分析问题，建立模型，然后运用数学知识对模型求解，最后根据计算结果来解决实际问题的过程[1]。线性代数中有许多概念抽象难懂，学生听得云里雾中，掌握不牢固，更是觉得学习相关知识没有什么用。所以，在讲解概念的过程中引入数学模型，有助于对概念的深入理解，起到事半功倍的作用[2]。将数学建模思想融入线性代数教学过程中，理论联系实际，不仅活跃课堂气氛，调动学生学习积极性，而且利用数学模型，变抽象为具体，有利于培养学生的数学应用能力。下面通过引入数学模型来诠释线性代数中矩阵的定义、矩阵相乘、矩阵的逆等知识点。

2 数学建模案例研究

例1[3]：某航空公司在A、B、C、D共4个城市之间开通若干条航线，这4个城市间的航班通行情况如下图所示。若有航班通行用“1”表示，无航班通行用“0”表示，则根据这4个城市之间的通行情况建立如下表1。问题：中转一次可以使C城市和D城市之间通航吗？

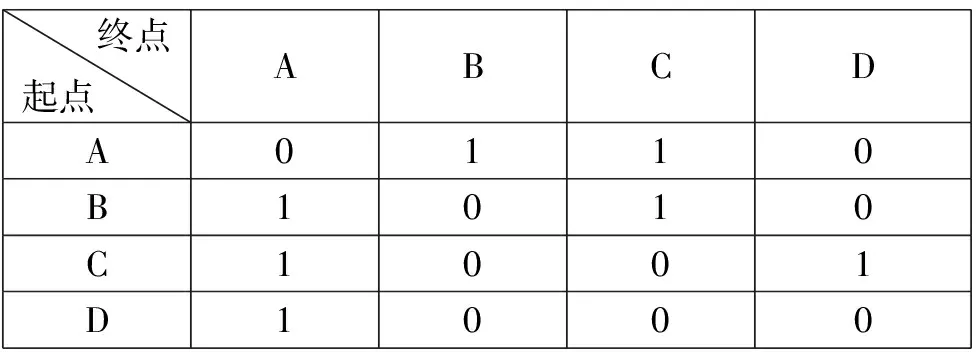
表1

分析：用图表示通行情况存在一定的弊端，比如当城市无限增多时，图形看起来很复杂。而换用表格表示，则只需增加相应行和列即可，此时恰好引入矩阵的概念，并利用表格说明矩阵的特点，矩阵是个数表，而且数表里面的元素不能随意变换位置。例1用矩阵就可以表示为:

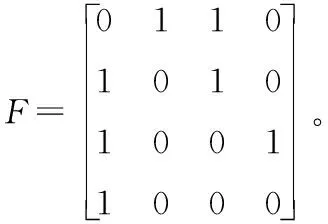
解：城市ABCD用数字1234表示，矩阵F中的元素fij等于1表示两个城市之间可以通航，等于0表示两个城市之间不能通航。则图或者表格可以表示为矩阵F，下面求中转一次两个城市之间的通行情况:

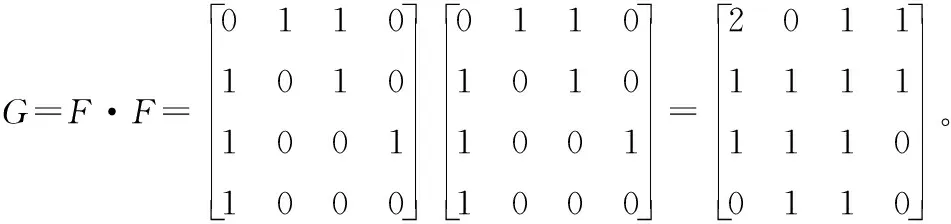
矩阵G中的元素gij表示从城市i到城市j中转一次的路线条数，b34=0表示从城市C到城市D中转一次不能通航；b43=1表示从城市D到城市C中转一次只有1条路线，D→A→C。

例2：线性代数课程的综合成绩是由考勤、提问、作业和末考构成的，分别占比10%、10%、20%和60%。已知甲、乙、丙、丁四名同学考勤、提问、作业、末考成绩如下表2所示，问题：四名同学成绩从高到低的顺序是什么？

表2

分析：将甲、乙、丙、丁四名同学的每项成绩乘以相应比例可得综合成绩，可以写出两个矩阵，第一个矩阵行表示四名同学，列表示各项成绩，第二个矩阵只有一列表示各项成绩占比，最后再相乘。

解：由题意可设以下两个矩阵:

由矩阵相乘可得:

C即为四名同学的综合成绩，从结果易得：第一名是甲，第二名是乙和丙，第三名是丁。

计算过程可借助Matlab软件，编写程序：

A=[100 90 90 82；100 95 95 78；85 90 90 83；90 90 80 85]；

B=[0.1；0.1；0.2；0.6]；

C=A*B

按Enter键，就可得结果为:

C=

86.2000

85.3000

85.3000

85.0000

从这个例题可以看出，末考成绩第一名其综合成绩并不是第一名，末考成绩最后一名其综合成绩是第二名，此时教育学生不要只为考试而学习，要注重平时学习的重要性，学习是持续性的，不是一蹴而就的。

例3：为确保传递信息的保密性，往往会对传输信息进行加密再解密，可得知传递的原信息。例如，若要传递信息stop，我们可采取26个英文字母与数字对应的加密法。假设26个英文字母与数字之间建立一一对应关系

分析：已知C=AB，求B，首先求A-1，再求B=A-1C，根据字母与数字的对应关系，就可以知道原传输信息内容。

解：根据伴随方阵法或者初等变换法求A-1，

方法一：伴随方阵法

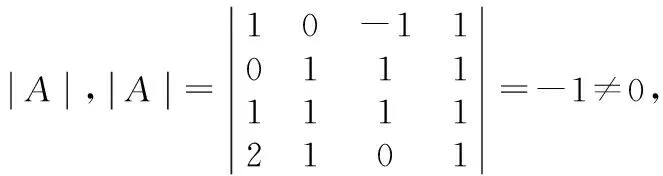
A11=0，A21=1，A31=-1，A41=0，A12=1，A22=-2，A32=3，A42=-2，A13=0，A23=1，A33=-2，A43=1，A14=-1，A24=0，A34=-1，A44=1，

方法二：初等变换法

所以:

根据字母与数字的对应关系，7，15，15，4对应的字母为g，o，o，d，可得原传输信息为good，以上为解密过程。

利用Matlab软件可求A-1和B，程序为：

A=[1 0 -1 1；0 1 1 1；1 1 1 1；2 1 0 1]；

inv(A)

ans=

B=[0 -1 1 0；-1 2 -3 2；0 -1 2 -1；1 0 1 -1]*[-4；34；41；33]

B=

结语

在线性代数教学过程中融入数学建模案例，使知识变得直观化、具体化，通过实际问题和数学联系起来，使学生更容易接受新知识，将实际问题转换为数学问题来解决，从而提高学生分析问题、解决问题的能力。在数学建模案例选取过程中，需要注意以下几点：(1)根据学生的接受能力选取适当的案例，不易太难。(2)根据学生的专业选取合适的案例，使学生能够将数学知识融入专业知识中，使后续的专业课学习更加得心应手。那么，如何有效地将数学建模思想融入线性代数课程的教学过程中，这是一个长期的、需要不断探索的、潜移默化的过程。因此，应逐步将数学建模与线性代数教学有机结合，将学与用有机结合，将专业基础知识教育与培养学生综合素质、创新能力、应用能力有机结合[4]，这对培养应用型人才具有很大的促进作用。