柴达木盆地蒸散发遥感估算与耗水有效性评价

涂晨雨,贾绍凤,朱文彬,*,吕爱锋,官云兰

1 中国科学院地理科学与资源研究所,陆地水循环及地表过程重点实验室, 北京 100101

2 东华理工大学测绘工程学院, 南昌 330013

我国西北干旱内陆区地处欧亚大陆腹地,是全球气候变化的生态脆弱区,也是丝绸之路经济带建设的核心区[1—2]。面对经济社会发展与生态环境保护的用水矛盾,水资源短缺成为制约该地区长远可持续发展的关键因子。从水资源消耗的角度来看,干旱区80%的降水通过蒸散发形式耗散[3—4]；对于人类社会而言,农业用水占我国用水总量的60%左右,其绝大部分也是以农田灌溉的形式消耗于蒸散发。因此,准确估算干旱区的陆面蒸散发,掌握其时空变化特征,对于该地区的水资源合理利用与生态文明建设具有重要意义[5—7]。

陆面蒸散发(Evapotranspiration,ET)是土壤蒸发与植被蒸腾之和。考虑到ET在水文学、气象学、生态学和农学等诸多领域中的重要作用,国内学者在我国西北干旱区蒸散发研究方面已取得较多成果,概括为以下3个方面：一是站点尺度典型生态系统蒸散发的观测与分析研究[8—10],二是区域尺度遥感蒸散发模型的研发与应用研究[11—13],三是基于蒸散发的水分利用效率评价与生态需水研究[14—16]。前两者为后者提供数据与方法支撑,后者是前两者的拓展应用。具体来说,基于涡度相关法、波文比-能量平衡法和称重法的站点观测技术,虽然可以实现ET的准确测量,对于把握典型生态系统局地的ET特征具有明显优势,但无法有效反映大尺度异质下垫面ET的空间变异性[17]。与之相反,遥感技术具有快速便捷、宏观性强等诸多优点,在获取区域尺度地表特征参数方面具有无可比拟的优势,因而成为当前大尺度陆面蒸散发模拟估算的主流方法[18—19]。当前关于遥感蒸散发模型的综述文章较多,分类也不尽相同[18,20]。根据模型内在的物理机制,基本可将其分为经验统计模型、能量平衡模型和特征空间模型三大类[21]。经验统计模型主要是基于蒸散发与遥感参量的统计关系进行模型研发,常用的遥感参量有植被指数、地表温度和反照率等；能量平衡模型通过净辐射、土壤热通量和显热通量的遥感估算,基于能量平衡方程余项计算法求得潜热通量,代表性模型有SEBAL模型[22—23]、SEBS模型[24]、TSEB模型[25]等；特征空间模型基于区域尺度地表温度、植被指数、反照率等遥感参量二维散点图的几何形态构建模型边界,进而通过插值算法获得像元尺度蒸散发。值得注意的是,上述模型虽然在过去几十年间获得了长远的发展,但仍然面临着共同的挑战。一是受云量对光学遥感的影响限制,上述模型一般只应用于无云条件下,陆面蒸散发的时空连续模拟方法仍待探索；二是上述模型在实际应用中以单源架构为主,如何构建双源遥感蒸散发模型,实现土壤蒸发和植被蒸腾的有效分离,尚缺乏成熟可靠的技术体系；三是针对我国西北干旱区这种实测资料稀缺的区域,如何摆脱实测资料匮乏的制约,发展完全基于遥感的蒸散发模型,仍面临较大困难。受制于上述挑战,当前我国西北干旱区基于蒸散发的水分利用效率评价仍以站点和灌区尺度为主,难以在区域尺度以时空连续的方式揭示蒸散发水分消耗的有效性,这严重制约了基于ET的水资源管理目标的实现[6]。

针对上述困难与挑战,本研究选定柴达木盆地这一高寒干旱内陆区为代表,利用MODIS(Moderate Resolution Imaging Spectroradiometer)遥感数据,构建了具有时空二维属性的地表温度-植被指数特征空间,在日尺度实现了陆面蒸散发的时空连续模拟,进而通过土壤蒸发与植被蒸腾的分离,从低效、中效和高效三个层次开展研究区水分消耗的有效性评价。

1 研究区及数据介绍

1.1 研究区概况

柴达木盆地处青藏高原东北部,介于90°16′—99°16′E、35°00′—39°20′N之间,四周被昆仑山、阿尔金山和祁连山环绕,平均海拔在3000 m以上,是我国四大盆地中海拔最高的盆地[26]。盆地总面积约为27.5万km2,整体呈干旱荒漠景观,自盆地边缘到中心依次分为高山、山地、戈壁、沙丘、细土平原带、盐沼、湖泊等地貌类型。从气候类型看,柴达木盆地属于典型的高寒干燥大陆性气候,各地全年太阳总辐射量均大于680 kJ/cm2,降水量总体在200 mm以下,并从四周山区向盆地内部递减[27]。图1展示了柴达木盆地地形分布状况。

图1 柴达木盆地地形状况及站点分布Fig.1 Topographic conditions and site distribution in the Qaidam Basin

1.2 数据来源

研究数据包括卫星遥感数据和气象实测数据两个方面。遥感数据采用的是MODIS系列产品。MODIS是搭载在Terra和Aqua卫星上的光学传感器,涵盖了从可见光到热红外的36个光谱波段。本研究采用的MODIS产品包括MOD03、MOD06_L2、MOD07_L2、MOD11A1、MOD13A2、MOD15A2和MCD43B3。其中,MCD43B3用于地表反照率(α)的提取,MOD13A2提供的归一化植被指数(NDVI)用于植被覆盖度(fc)估算,MOD15A2提取的叶面积指数(LAI)用于双源蒸散发模型的构建,而其他产品则主要用于地表净辐射的遥感反演。由于自然条件恶劣,柴达木盆地地广人稀,仅有九个国家气象站(图1)。本研究采用的地面实测资料包括这九个气象站的空气温度、相对湿度、风速与蒸发皿数据。

2 研究方法

本研究首先利用单源遥感蒸散发模型进行蒸散发的总体遥感估算,进而基于双源蒸散发模型的理论框架,实现土壤蒸发与植被蒸腾的分离,最后通过土壤蒸发的进一步分离,开展蒸散发水分消耗的有效性评价。上述三部分的具体研究方法如下。

2.1 蒸散发的遥感估算

图2 地表温度-植被指数特征空间法示意图[30]Fig.2 A conceptual sketch of the trapezoid Ts-VI space[30] Tsmax：纯裸土在极端干旱条件下的最大地表温度 maximum land surface temperature of the extremely dry bare soil；Tsoil：纯裸土地表温度 land surface temperature of the bare soil；Tw：充足水分供给条件下的地表温度 land surface temperature under unlimited water access conditions；Tcanopy：植被完全覆盖条件下的地表温度 land surface temperature of full vegetated canopy；Ts：地表温度 land surface temperature；fc：植被覆盖度 fractional vegetation cover

本研究采用的遥感蒸散发模型为地表温度-植被指数特征空间法[28—31]。该方法的基本假设是,若研究区内存在着足够多充分反映土壤湿度与植被覆盖度变化情况的像元,则由地表温度(Ts)和植被指数(VI)构成的二维空间,将形成具有物理意义的三角形或梯形(图2)。该形状的上下边界称为干湿边界,分别代表蒸散发的最小和最大速率,每个像元的蒸发比(潜热通量占地表总的可利用能量的比值)可以根据其在干湿边界中的相对位置,通过线性插值的方法求得。根据蒸发比(EF)的定义,在日尺度土壤热通量(G)忽略的前提下,日蒸散发(ET)的估算公式如下：

ET=Rn,day×EFday

(1)

式中,Rn,day为日尺度地表净辐射；EFday为日尺度蒸发比,可用卫星过境时刻的瞬时蒸发比近似代替[32]。

2.1.1瞬时蒸发比的遥感估算

本研究瞬时EF的估算方法是Jiang & Islam[33]根据Priestley-Taylor方程[34]提出的,具体公式如下：

(2)

式中,Δ表示饱和水汽压随气温(Ta)变化的斜率；γ是湿度计常数；φ作为一个无量纲变量,反映的是空气动力学和地表阻抗信息,是特征空间法EF求解的关键参数。具体来说,各个像元对应的φ值主要由土壤湿度决定,从干边向湿边由0逐渐增大到1.26。对于纯植被而言,由于冠层的热力学属性和显著的蒸腾降温作用两方面原因,其表面温度与空气温度处于平衡状态,两者基本接近,因此纯植被像元的φ值(φcanopy)恒等于1.26。而对于纯裸地的φ值(φsoil),借助于反映地表土壤湿度的修订型温度植被干旱指数(MTVDI),求解公式如下：

φsoil=1.26[1-exp(MTVDI-1)]

(3)

基于此,混合像元的φ值以植被覆盖度(fc)为权重,通过线性插值的方法求得：

φ=φsoil(1-fc)+φcanopyfc

(4)

本研究根据Gillies等[35]提出的方法,利用NDVI来估算fc,公式如下：

(5)

式中,NDVImin和NDVImax根据Zhu等[36]的研究,分别设为0.05和0.86。

2.1.2MTVDI的求解

Sandholt等[37]通过研究特征空间与土壤湿度之间的经验关系,提出了表征土壤湿度的温度植被干旱指数(TVDI)。然而Sun等[38]研究表明这种经验性的TVDI存在着较大的主观性,因此提出了改进型温度植被干旱指数(ATVDI),其中ATVDI的求解需要分别构建纯裸地和纯植被的地表能量平衡方程。在此之后,Zhu等[39]研究发现纯植被地表能量平衡方程的构建涉及复杂的参数化方案,具有较大的不确定性,进而对TVDI进行改进,提出修订型温度植被干旱指数(MTVDI),公式如下：

(6)

式中,Tsmax和Tw分别代表纯裸土在极端干旱和充足水分供给条件下所能达到的地表温度,两者构成了特征空间的干湿边界；Tsoil为任意像元通过温度分解求得的纯裸土地表温度,求解公式如下：

(7)

式中,Tcanopy为植被完全覆盖条件下的地表温度,可用近地表空气温度Ta近似代替,Ta根据Zhu等[40]提出的方法由MOD07_L2和MOD06_L2产品求得。Tsmax根据地表能量平衡原理,并参考Sun等[38]、Long & Singh[30]和Zhu等[31]的研究,求解公式如下：

(8)

式中,下标“s”和“d”分别表示相关参数是纯裸土在极端干旱条件下求得的。其中,σ、εss、ρ、cp和cs分别为斯蒂芬-玻尔兹曼常数、裸土地表发射率、空气密度、空气定压比热容和纯裸土土壤热通量占地表净辐射的比例,五者均为常数；Sd和εa分别表示下行太阳辐射和空气发射率,其遥感反演方法参见Bisht & Bras[41]；ras和Tasd分别表示裸土的空气动力学阻抗及在极端干旱条件下的空气温度,ras通过风速求得,Tasd参考Szilagyi等[42]的研究成果,求解公式如下：

(9)

(10)

式中,Td和Twb分别表示露点温度和湿球温度,e*表示对应温度的饱和水汽压。Td参考Bisht & Bras[41]等的研究方法由MOD07_L2产品求得。

传统特征空间法并未给出Tw的理论求解公式,一般选用水体、茂密植被等特定像元的地表温度值近似代替[38,43]。这不但增强了该方法的经验性,而且在很大程度上限制了其在柴达木盆地这类植被覆盖稀疏地区的应用。基于此,本研究参考Szilagyi[44]对于湿润环境表面温度的求解方法,将Tw用卫星过境时刻对应的湿球温度(Twb)近似代替。

2.1.3日地表净辐射的估算

在瞬时地表净辐射(Rn)遥感反演的基础上,本研究采用Rivas & Cormora[45]提出的经验公式进行Rn,day的估算,公式如下：

Rn,day=0.43Rn-54

(11)

式中,全天气条件下Rn的求解是完全基于MODIS产品实现的,具体参数化方案详见Bisht & Bras[41]和余晓雨等[46]。

2.2 土壤蒸发与植被蒸腾的分离

虽然Bisht & Bras[39]提供的参数化方案可以实现全天气条件下Rn的遥感估算,但特征空间法对EF的求解需要Ts和VI两个关键参数,这决定了该方法只能求得晴天条件下非水体像元的EF值。有云条件下EF的估算一直是遥感蒸散发模型面临的一大难题,关于云量对EF稳定性的影响也存在一定的争议。Santos等[47]和Farah等[48]的研究表明EF在5—10天具有一定的稳定性。基于此,本研究通过线性插值的方法获得相邻有云天的EF数据,最终实现陆面蒸散发的时空连续估算。在ET已知的前提下,计算土壤蒸发与植被蒸腾的任一组分,通过差值的方法即可实现另一组分的求解。柴达木盆地地处干旱区,总体的植被覆盖度极低,因此本研究重点对土壤蒸发进行估算。具体分为三步：第一步是土壤净辐射(Rn,soil)的计算,参考Purdy等[49]提出的参数化方法,估算公式如下：

Rn,soil=Rne(-kRnLAI)

(12)

式中,经验参数kRn为0.6。第二步是土壤蒸发比的计算,由公式(2)和(3)联合求得。第三步是日尺度土壤蒸发的计算,可参考公式(1)实现。

2.3 耗水有效性评价

在土壤蒸发与植被蒸腾分离的基础上,本研究采用王浩等[50]提出的土壤水资源消耗效应评价指标体系,进行柴达木盆地耗水有效性评价。具体来说,蒸散发的水分消耗效应被分解为三个部分：植被蒸腾直接参与干物质形成,被认为是高效耗水；植被棵间的土壤蒸发虽然并未直接参与干物质生成,但是具有调节植被生长小气候的作用,可认为是中效耗水；而在柴达木盆地广泛存在的盐壳、戈壁和沙漠等,常年属于无植被区,这些地区的土壤蒸发被认为是低效耗水。由此可见,为了实现低效耗水与中效耗水的分项评价,还需进一步将土壤蒸发进行分离。本研究以公式(5)求得的多年平均植被覆盖度为依据,将fc接近于零的土壤蒸发定义为低效耗水,将fc高于零的土壤蒸发定义为中效耗水。

3 结果与讨论

3.1 蒸散发精度评价与时空分布特征

3.1.1蒸散发估算精度评价

由于缺乏蒸散发实测数据,本文主要是通过与现有蒸散发产品的对比分析来进行精度说明。虽然当前国外机构已发布了多种全球尺度的遥感蒸散发产品,譬如MOD16A2、GLEAM与SSEBop等,但这些产品或者空间分辨率较低,或者在柴达木盆地存在数据缺失。鉴于此,本研究基于国内外蒸散发模拟研究的发展前沿,选用了两套由国家青藏高原科学数据中心发布的、相对较新并且具有较高空间分辨率的蒸散发产品作为参考。一套为Zhang等[51]通过总初级生产力与蒸散发耦合模拟生成的全球500m、8d时间尺度蒸散发产品,另一套为马宁等[52]基于蒸散发互补模型建立的我国0.1°分辨率、月尺度蒸散发产品,该产品的气象输入是由我国气象实测数据同化得到的。可以看出,这两套产品无论是在空间分辨率还是输入数据的准确性方面都有明显优势。与本研究相比,两者均未提供日尺度数据,因此仅从年尺度和月尺度两个方面来进行精度评价(图3)。从三组数据年尺度对比分析结果可以看出,前四年三者具有较好的一致性,此后2016—2018年,Zhang等人估算结果总体偏大,而马宁的数据虽然缺少两年,但整体与本研究结果比较接近。从本研究估算结果与马宁等的数据集在2011—2017年间月尺度对比的情况来看,两组数据平均绝对误差(MAE)、均方根误差(RMSE)和偏差(Bias)分别为4.04 mm、5.39 mm和0.58 mm,相关系数(r)高达0.96,具有显著的正相关性。此外,虽然蒸发皿观测数据代表的是潜在蒸散发,其数值在柴达木盆地这类干旱区远远高于实际蒸散发,但在实际蒸散发实测数据匮乏的条件下,两者之间的对比也具有一定程度的验证作用。图4为九个气象站2011—2019年间月尺度两者的散点图,可以看出两者在站点尺度具有很好的正相关性,r在0.52—0.85之间。基于以上两方面综合评价,本研究估算结果达到了一定的精度要求,可用于分析柴达木盆地蒸散发时空分布特征。

图3 本研究蒸散发估算结果与现有产品的对比分析Fig.3 Comparison of the ET estimation in this study and other existing productsET:蒸散发 Evapotranspiration

图4 站点尺度月蒸散发估算值与蒸发皿实测值之间的散点图Fig.4 Scatterplots of monthly estimated evapotranspiration and observed pan evaporation at site scale

3.1.2蒸散发时空分布总体特征

柴达木盆地2011—2019年蒸散发时间变化趋势如图5所示。盆地年蒸散发变化范围在173.04—205.99 mm之间,多年平均值为188.75 mm。从年际变化看,盆地蒸散发近九年整体呈现先减少后增加趋势,标准差为9.62 mm/a。从月际变化看,九年蒸散发年内变化趋势非常接近,均呈显著单峰型。1—5月盆地蒸散发持续增加,于6月或7月达到顶点,之后逐渐下降。2011年,月蒸散发最小值出现在1月,其余年份月蒸散发最小值均出现在12月。总体来说,4—9月份是盆地蒸散发的集中期,这6个月的蒸散发约占全年蒸散发的80%。

图6是柴达木盆地蒸散发空间分布图,可以看出盆地蒸散发地域分异特征显著,具有明显的从东南向西北减少的趋势。这种差异主要是由盆地降水量的空间格局决定的。具体来说,盆地降水整体表现为东部大于西部,四周山区高于盆地内部,这与本研究蒸散发的空间分布特征非常吻合。对于盆地内部而言,蒸散发高值受局部水文条件影响,多出现于盆地中部的地下水出流带以及河流湖泊等水体附近(如达布逊湖、托素湖、托索湖、柴达木河等),呈亮斑及条带状分布。

图5 柴达木盆地2011—2019年蒸散发时间变化趋势Fig.5 Temporal variation of ET in Qaidam Basin from 2011 to 2019

图6 柴达木盆地多年平均蒸散发空间分布图Fig.6 Spatial distribution of annual average ET in Qaidam Basin

3.2 土壤蒸发与植被蒸腾分项评价

图7为柴达木盆地2011—2019年土壤蒸发与植被蒸腾时间变化趋势图。土壤蒸发多年平均值为171.06 mm,植被蒸腾多年平均值为14.26 mm,两者分别占总蒸散发的92.3%和7.7%。根据本研究的估算结果,柴达木盆地总体的植被覆盖度仅为4%,因而盆地整体的植被蒸腾量远远低于土壤蒸发量。就年际变化来看,土壤蒸发年际波动明显,变化趋势与盆地蒸散发一致,整体呈单谷型,最大值出现在2012年(188.36 mm),最小值出现在2016年(156.41 mm),标准差为9.16 mm/年；而植被蒸腾与盆地蒸散发年际变化并非完全一致,两者在2014—2016年以及2019年期间的变化趋势相反。在年内变化方面,土壤蒸发与植被蒸腾均呈单峰型,与降水量年内分配不均相一致；然而植被蒸腾峰值出现时间(7月份)总体比土壤蒸发(6月份)晚1个月,具有明显的滞后效应。

图8是土壤蒸发与植被蒸腾空间分布以及两者分别占总蒸散发的比例分布图。具体来说,土壤蒸发的空间分布趋势与盆地总的蒸散发接近,具有明显的由西北向东南增大、从盆地内部向四周山区增加趋势；对于植被蒸腾而言,由于盆地内部属于无植被区,而在外部呈现半环状植被分布带[53],因此植被蒸腾的空间分布极不均匀,主要集中在盆地东南部,整体呈向西北开口的半环形,并在局部地区受河流及地下水等影响,具有间断条带状分布特征。从土壤蒸发与植被蒸腾占蒸散发的比例分布可以看出,两者具有显著的互补效应,土壤蒸发占比在39%—100%之间变动,高值区广泛分布于盆地内部及西北部的无植被地带；植被蒸腾占比在0—61%之间变动,这意味着在1 km的栅格尺度研究区尚无纯植被覆盖像元,其空间分布受植被覆盖度控制,高值集中分布在盆地东南部以及祁连山和昆仑山的部分山区。

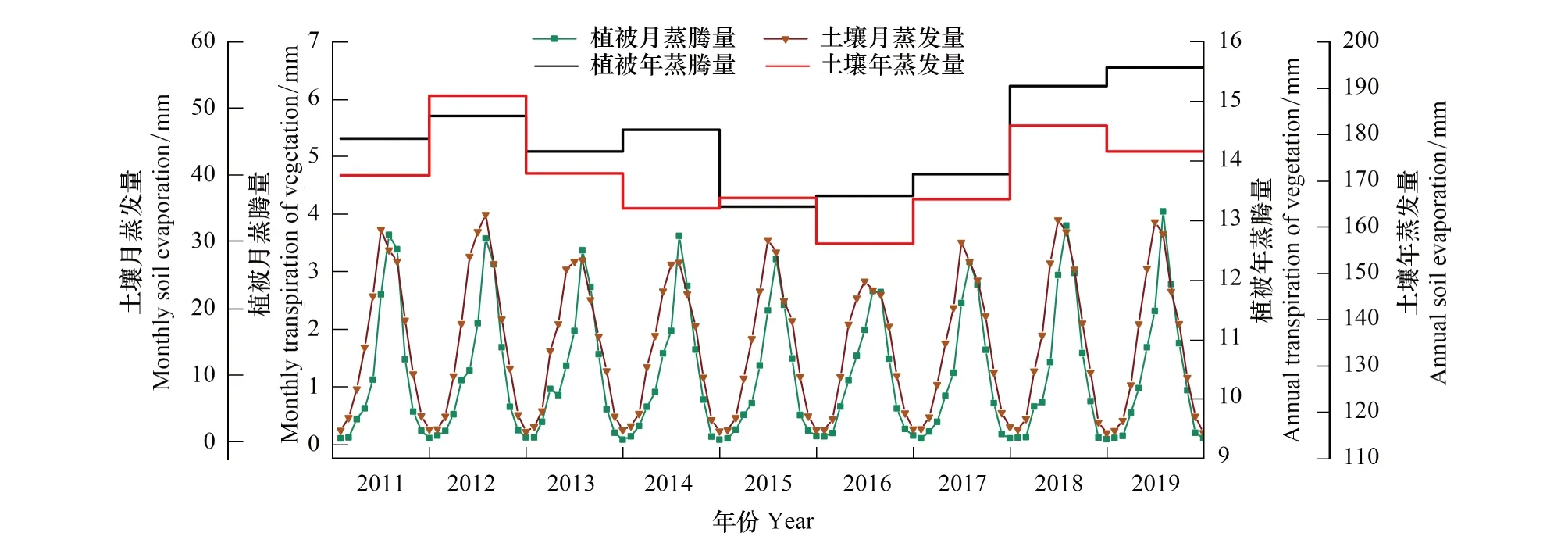
图7 柴达木盆地2011—2019土壤蒸发与植被蒸腾时间变化趋势Fig.7 Temporal variation of soil evaporation and vegetation transpiration in Qaidam Basin from 2011 to 2019

图8 柴达木盆地土壤蒸发与植被蒸腾空间分布及占比图Fig.8 Spatial distribution of soil evaporation and vegetation transpiration as well as their corresponding proportion in Qaidam Basin

3.3 自然生态系统耗水有效性评价

表1是根据土壤水资源消耗效应评价指标体系,对柴达木盆地2011—2019年自然生态系统耗水有效性评价的结果。具体来说,盆地自然生态系统多年平均耗水总量为430.94亿m3,耗水量大小按有效性排序依次为中效耗水>低效耗水>高效耗水,三者分别为226.55亿m3、176.17亿m3和28.22亿m3,占总耗水的比重分别为52.57%、40.88%和6.55%。高效、中效及低效耗水量年际变化整体均呈单谷型,即两端年份(2011—2012年和2018—2019年)高而中间年份(2013—2017年)低。其中,低效与中效耗水年际变化与盆地耗水总量年际变化相吻合,而高效耗水与耗水总量年际变化趋势相比存在一定差异,2014年高效耗水量增加,耗水总量减少；而2015年高效耗水量减少,耗水总量增加。此外,由于柴达木盆地自然景观以荒漠、戈壁及盐壳为主,植被覆盖度极低,因而盆地整体的高效耗水占比远远低于中效耗水和低效耗水。然而就单位面积高、中、低效耗水情况而言,三者耗水量分别为297.83 mm、252.83 mm和132.23 mm。可以看出,单位面积纯植被耗水实际要高于单位面积纯裸土耗水；而就中效耗水与低效耗水而言,两者虽然都是纯裸地耗水,但是植被株间的裸地耗水远远高于无植被区。

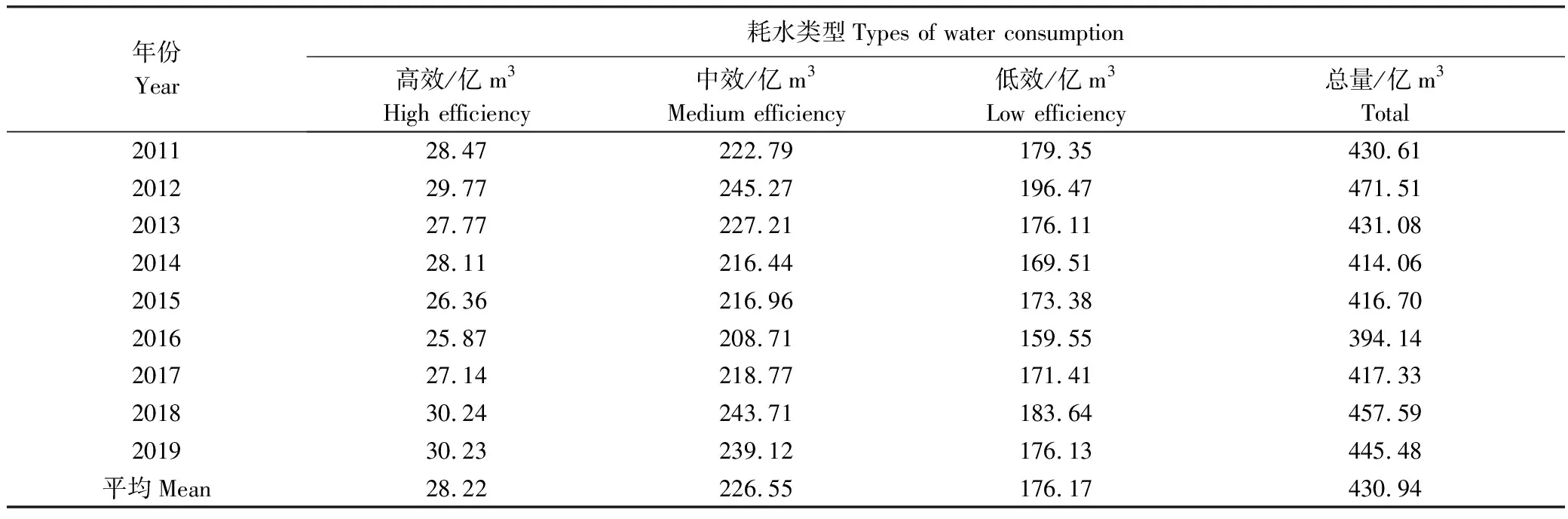
表1 柴达木盆地2011—2019年耗水有效性评价统计结果

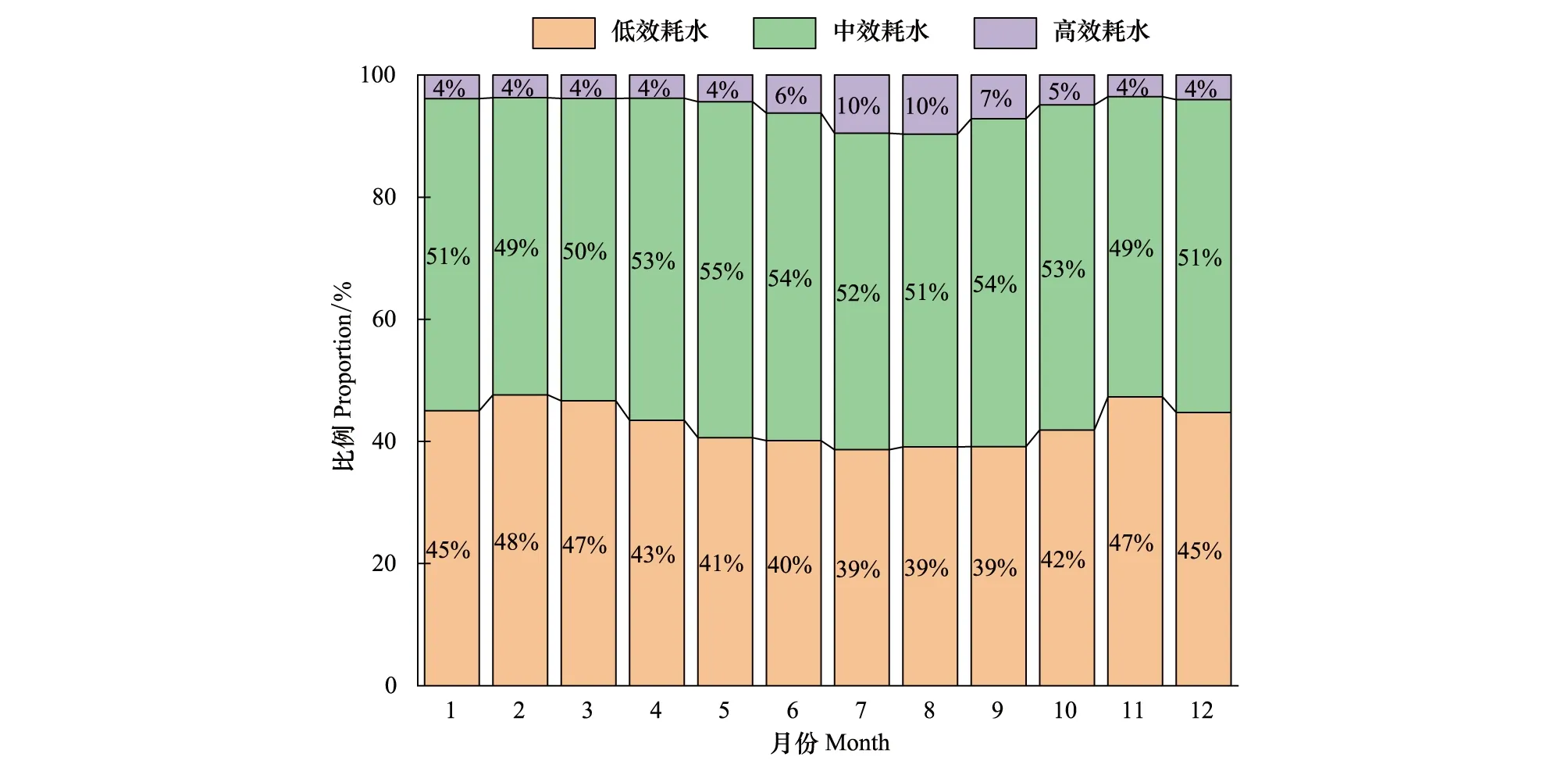
图9 柴达木盆地不同等级耗水量逐月占比情况Fig.9 Monthly proportion of water consumption with different efficiency in Qaidam Basin

图9是高、中、低效耗水量多年平均的逐月占比情况,其中高效耗水占比在3.57%和9.68%之间,具有明显的生长季高于非生长季特点,呈单峰型变化；低效耗水占比在38.63%到47.63%之间,则具有明显的非生长季高于生长季特点,表现为单谷型；而中效耗水占比在48.63%到55.01%之间,呈现双峰型,耗水量占比于3—5月(春季)显著上升,而6—8月(夏季)及10—11月具有明显下降趋势。

4 结论

本研究针对干旱内陆区实测资料匮乏的现状,利用特征空间法实现了柴达木盆地逐日陆面蒸散发的遥感估算,进而通过土壤蒸发与植被蒸腾分离技术研发和土壤水资源消耗效应评价指标体系构建,以时空连续的方式揭示了土壤蒸发与植被蒸腾的时空变化特征,评价了自然生态系统水分消耗的有效性。主要结论如下：

(1)近九年,柴达木盆地蒸散发总体呈先减少后增加趋势,多年平均值为188.75 mm,年内变化则呈现为单峰型分布,4—9月蒸散发占比达到80%。受降水空间格局影响,蒸散发具有明显的空间异质性,整体表现为东部大于西部,四周山区高于盆地内部,盆地内部高值区主要集中在湖泊、河流及地下水出流带等水体附近。

(2)盆地多年平均土壤蒸发与植被蒸腾分别为171.06 mm和14.26 mm,分别占总蒸散发的92.3%和7.7%。两者年内变化趋势一致,但植被蒸腾达到峰值的时间总体比土壤蒸发晚一个月,滞后效应显著。土壤蒸发空间格局与盆地总蒸散发相一致,而植被蒸腾整体呈东南向西北开口的半环形,并在局部地区具有间断条带状分布特征。

(3)盆地多年平均耗水总量为430.94亿m3,其中高效、中效和低效耗水的占比分别为6.55%、52.57%和40.88%。盆地植被覆盖度较低,因而高效耗水总量远远低于中效和低效耗水。然而就单位面积而言,三者的耗水量分别为297.83 mm、252.83 mm和132.23 mm,纯植被耗水和植株间土壤耗水均远远高于无植被区裸土耗水。