Mathematica在化学群论教学中的应用

周佳，魏梦娇

哈尔滨工业大学(深圳)理学院，广东 深圳 518055

群论是高等院校化学相关专业结构化学课的重要组成部分，也是其中教学的一个难点[1]。群论部分主要包括对称操作和对称元素、对称操作群、分子点群、群的表示等内容。这一部分的特点就是比较抽象，需要较强的空间想象能力，这些特点对于学生在课堂上充分理解掌握群论知识增加了难度，实际教学中往往需要教师在课下布置大量的作业才能获得满意的教学效果，不利于激发和培养学生的学习兴趣和学习主动性。然而，群论在化学中的应用已经十分广泛和普遍，学习掌握群论知识对化学相关专业的学生在今后科研实践中判断分子结构、推测分子性质都起着举足轻重的作用。

随着计算机技术的迅猛发展，当前越来越多的授课教师采用Mathematica软件来辅助课堂教学。例如，马安德等[2]在讲授分析化学中求解酸碱溶液pH时遇到非常复杂的酸碱体系，其质子平衡方程式会涉及一元N次方程，作者借用Mathematica软件进行求解不仅降低了方程求解的难度，也提高了计算的精度。赵文丽等[3]在大学物理教学中同样借用Mathematica研究了力学中单摆的小角问题以及电磁学中均匀带电细圆环场强和电势分布问题，将相关结论定量、直观地显示出来，提升了教学效果。杜迎春[4]针对化学反应工程通常涉及很复杂的数学模型，甚至需要对数学模型参数估值的特点，采用Mathematica求解非理想反应器轴向扩散模型的彼克列准数、对化学反应动力学的参数进行估值以及在设计反应器时预先进行模拟计算，这极大地降低了化学反应工程这门课的计算难度，提高了教学效率，提升了教学效果。量子化学是化学类课程中比较偏理论的专业课，对于学生而言难度也比较大，石卉等[5]在教学中运用Mathematica软件求解电子积分、Hartree-Fock方程以及绘制轨道图像，使原本复杂枯燥的理论变成可以应用的例子，激发了学生的学习兴趣，提高了学习效率。以上这些教学改革都表明Mathematica软件在课堂教学中具有显著优势。Mathematica自20世纪60年代由史蒂芬·沃尔夫拉姆主导设计研发以来，一直是应用最为广泛的数学软件之一，它能够很好地结合数值和符号计算引擎、图形系统、编程语言、文本系统以及其他应用程序的高级链接。Mathematica还是一种很好的可视化应用软件，可以很好地绘制二维、三维模型以及显示动画。因此，我们在群论课堂教学过程中采用Mathematica软件进行辅助教学，降低理论学习难度，使群论教学内容可视化和可操作化，更加形象地展示分子的对称元素以及对称操作，帮助学生理解与掌握分子的对称性以及对称操作，提升学生对群论课程的学习兴趣，进而提升教学质量。

1 C2v点群所属对称操作的表示矩阵和乘法表

对称元素以及对称操作是群论学习的基础。对称操作相当于将分子中的原子从原来的位置变换到新的位置而分子的结构保持不变。以往教学通常以黑板或者幻灯片加以演示。这里我们应用数学软件Mathematica进行教学。首先，通过Mathematica使用Molecule命令调出水分子(图1)。

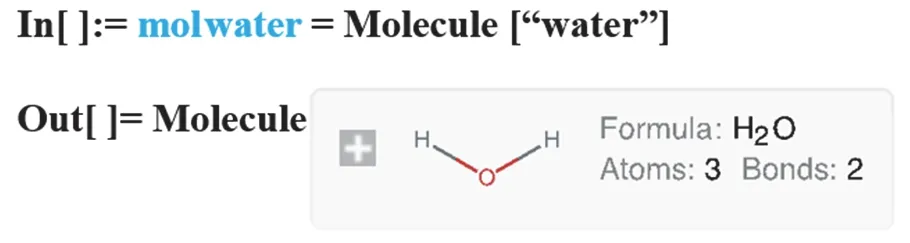
图1 Molecule命令调取水分子图

之后，使用MoleculePlot3D命令显示其三维结构(图2)。课堂上，可以通过鼠标进行旋转和移动等操作直观地观看分子。这里，水分子处在xy平面上。需要指出Mathematica内部还存储有大量其他分子，可供学生课后自行练习。

图2 水分子三维结构图

水分子有4个独立的对称操作(元素)，包括恒等操作、一个旋转操作和两个反映操作。通过前面的演示讲解，学生已经了解对称操作相当于空间坐标的线性变换，而数学中线性变换可以用矩阵来表示。通过对于4个对称操作进行分析，得到他们对应的变换矩阵(EU, C2,σxy,σyz)，如图3所示。水分子的4个独立的对称操作，组成了C2v点群，满足群的基本条件。群元素之间可能的乘积以表格形式列出，称为群的乘法表。群的乘法表是验证是否是一个合格群的重要标志，也是本部分学习的难点。这里，我们同样借助Mathematica构建C2v点群乘法表，如图3所示。结果表明，4个对称操作组成的C2v群，满足群的4条基本性质，即封闭性、恒等元素、结合律、逆元素。

图3 C2v点群乘法表

2 C3v点群分子对称操作的表示矩阵及其应用

水分子的各种对称操作比较容易被学生理解和掌握。接下来，笔者尝试带领学生一起深入分析更加复杂的分子结构。这里以氨分子作为例子，同样通过Mathematica使用Molecule命令调出其分子结构(图4)，但是我们应用AtomCoodinates自定义其中的原子坐标。

图4 Molecule命令调取氨分子图

通过MoleculePlot和MoleculePlot3D命令分别查看分子的二维(图5)和三维结构(图6)。同样，可以通过鼠标进行旋转和移动等操作直观的观看分子的三维结构。

图5 氨分子二维结构图

图6 氨分子三维结构图

通过自定义坐标，我们把N原子放置在z轴(0, 0, 1)位置，其中一个氢原子放置在x轴(1, 0, 0)位置，另外两个氢原子通过简单计算得到它们的位置和。定义了氨分子中原子坐标之后，通过AtomList命令确认原子顺序，并采用矩阵的方式查看原子坐标(图7)。

图7 矩阵表示氨分子原子坐标图

氨分子的几何结构属于C3v点群，有6个独立的对称元素，包括一个恒等操作、三个反映操作以及两个旋转操作。其对应的矩阵表示如下：

之后通过将对称矩阵与原子坐标相乘，查看各个原子位置的变化(图8)。与图7对比，发现3个氢原子彼此交换位置，而氮原子的位置保持不动。

图8 氨分子对称操作示例

同样，氨气分子的6个独立的对称操作也构成了一个封闭的C3v点群，可以用群的乘法表加以验证，这个验证留给学生自行编写Mathematica程序完成。此外，Mathematica程序还可以用来方便求解矩阵的特征标以及分解可约表示，这些我们在下面水分子的振动光谱中演示。

3 水分子的振动光谱

水分子属于C2v点群，前面我们已经获得了各种对称操作所对应的矩阵。这里我们应用已获得结果来研究水分子的振动光谱。我们已知水分子中每个原子都有3个运动自由度，如图9所示。把对称操作对应的矩阵作用到每个原子的运动自由度，得到一个矩阵，也就是我们前面得到的EU，C2，σxy，σyz四个矩阵，这样我们就得到4个对称操作的矩阵，每个矩阵包含9个运动自由度。同时，水分子本身3个原子也要像前面氨分子和对称矩阵作用，结果原子坐标发生变换。我们这里以C2对称操作为例加以详细说明。

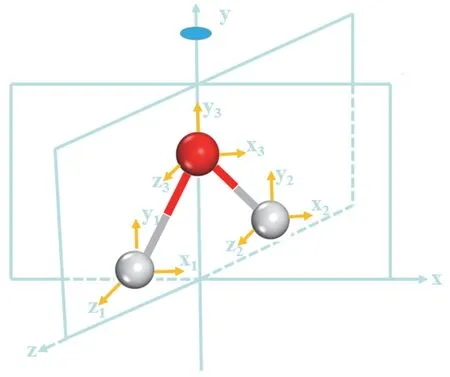
图9 水分子及各个原子运动自由度示意图

C2对称操作所对应的为C2= {{-1, 0, 0}, {0, 1, 0}, {0, 0, -1}}，每个原子都有一个C2，最后构成9 × 9的矩阵如图10左侧所示。考虑到C2对称操作使得H1和H2交换位置，对应为分块矩阵的第2行和第3行交换位置，因此最终C2对称操作得到的矩阵为图10右侧。

图10 C2对称操作示例图

之后通过Mathematica程序中Tr命令得到矩阵的迹，为-1，也就是特征标。最终四种对称操作所得到的可约表示的特征标为{9, -1, 3, 1}，对应{EU, C2,σxy,σyz}。此后，通过Projection命令将可约表示分解成不可约表示。这里以投影到B1{1, -1, 1, -1}为例，得到结果为3：

最后得到可约表示可以分解为不可约表示的和3A1+ A2+ 3B1+ 2B2。水分子的3个原子的运动通过线性组合构成平动、转动和振动，共9种。去掉平动的A1+ B1+ B2和转动的A2+ B1+ B2，最后振动的3个模式为2A1+ B1。将A1和B1对应的特征标作用到水分子即可得到水分子的3种振动方式，这里建议使用内坐标(键长和键角)，可以更加方便和直观地得到相应的振动方式，和教科书上的结果一致。

4 结语

群论是结构化学课教学的一个重点，也是难点，需要一定的数学基础和较强的空间想象能力。应用数学软件Mathematica展示分子构型、探索分子对称性，解决相关化学问题，降低了群论部分的学习难度，有利于学生对群论知识的理解和掌握，同时激发学生对群论的学习兴趣。数学软件Mathematica并不需要学生具备很好的数学或者编程基础，命令行与传统数学接近，便于学生理解和掌握，也利于培养学生的数学素养，以及未来应用数学工具解决化学相关问题的能力。