介质扰动对声波的调制效应-参量接收阵及其他

李颂文

（水声对抗技术重点实验室；上海船舶电子设备研究所，上海 201108）

0 引言

声传播本身就是一种介质扰动过程。本文标题中所谓的介质扰动，指的是所考察声波本身之外的介质扰动，可以是其他声波产生的，也可以是一般的流体运动带来的。介质扰动造成了介质的不均 匀，声波在不均匀介质中传播则会产生声散射。当介质的不均匀具有时间周期性时，则可能对声波产生调制效应，衍生出稳定的、新的频率的声波。

当一列声波由于另一列声波造成的介质不均匀而产生声散射时，一般称为“声散射声”[1]，可以产生频率为两列声波的和频及差频的散射波，水声工程中广泛应用的“参量阵”、以及曾经颇受关注的“参量接收阵”就是基于这种物理现象。而其他因素造成的流体中介质周期性扰动，如海洋中的内波、表面重力波等，可以形成非常大的介质不均匀散射体，对远距离声传播造成重要影响，也可能对声传播产生调制效应；其中由水下运动目标扰动流体而产生的这种效应，某些条件下也许具有非常显著的可观测性，因而或许可用于对水下运动目标进行间接探测的现象。

本文主要探讨两方面内容：（1）从水下目标辐射的低频声波对已知高强度高频声波的调制效应（参量接收阵）角度，介绍一种对低频声信号实现极高增益接收的方式；（2）从号称由于潜艇操纵而产生的不可避免的极低频、大尺度水波对已知声波的调制效应角度，介绍一种可能实现对潜艇超远程警戒的水声探测方法。另外，文章还基于声散射声现象，简单分析了利用高强度声波对某个单频声信号的吸收作用。

1 Lighthill 波动方程

Lighthill 在处理气体喷流噪声问题时提出了声类比理论[2-3]，为流动声的研究奠定了理论基础，其广为所知的Lighthill 波动方程，由于在处理声波相互作用问题上具有非常直观的物理意义且便于数学求解计算，在非线性水声学的研究中也起到了非常重要的作用。水声工程领域获得广泛应用的参量阵概念也因此而出现。

Lighthill 方程的表达式为

式中：ρ为流体密度；C0为介质中的声速；T为应力；x为笛卡尔坐标量，下标i，j=1,2,3 分别代表笛卡尔坐标系的三个坐标轴。

忽略粘滞效应，应力Tij满足：

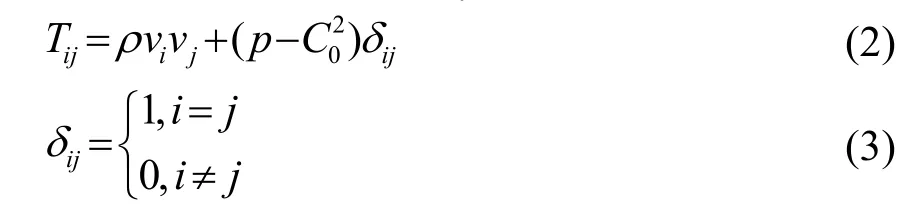
式（2）中的第一项是雷诺应力，由质点运动效应产生，第二项是波动过程中的温度效应，由物态方程决定。

方程（1）的右边是应力Tij的二阶导数，如果不为0，则方程（1）是非齐次波动方程，相当于存在密度波的辐射源。此方程有密度关于应力Tij的积分解：

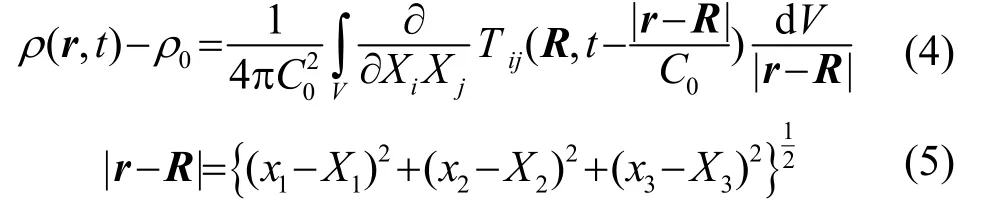
式中：r和R分别表示场点和源点。

而对于我们感兴趣的两列声波（或一列声波与一列水波）的相互作用，在合理的热力学假设（物态方程）下，应力Tij是已知的，积分空间也是已知的，因此声场可以通过式（4）积分求出。这就是基于Lighthill 方程研究声散射声、由声散射声衍生出的参量阵和参量接收阵的物理和数学基础。基于此方程，也可以研究水波对声波的散射效应。

2 参量接收阵

2.1 声散射声和声吸收声

最早将Lighthill 波动方程应用于声散射声研究的是美国麻省理工学院声学实验室的Ingard 和Pridmore-Brown[4]。他们根据Lighthill 方程的积分解计算了两列频率不同、传播方向互相垂直的声波的互作用声场，并通过实验测量到了和频和差频声波。这个最早的实验相对比较粗糙，测得的散射声压不稳定，并且比理论计算值低10 dB 以下。Westervelt 随即发表了两篇文章[5-6]，对Ingard 和Pridmore-Brown 的研究结果表达了不同的看法。Westervelt 认为Ingard 和Pridmore-Brown 的两列准直平面波束（即限制在一定矩形范围内的平面波）假设不满足Lighthill 方程的推导条件，他们的理论结果很可能是准直波束假设所带来的不连续边界造成的，而实验结果则很可能测得的是直接从换能器发出来的差频及和频频率的声波（声散射声造成的次级声场本来就很弱，并不容易测量到），而实际上通过Lighthill 方程求得的差频及和频声是由达朗贝尔源产生的，只能发生在两列波束的互作用区域内，不可能传播到互作用区域外。随后针对这个问题的争论持续了30 多年，学者们发表了大量的文章[7-10]。1989 年，挪威卑尔根大学的Berntsen 和Tjotta 发表的基于更一般的非线性方程进行数值计算的结果[11]，针对之前的各种理论和实验给出了较全面的分析解释，之后似乎很少再有关于这个问题的争论文章。

既然两个声波相互作用后产生了新的和频及差频信号，那么原来的信号必然要有所损失，这个损失的部分也可以理解为被吸收了，即所谓的“声吸收声”。Westvelter[12]依据其修正的声散射声计算方法，得出声吸收系数的公式为

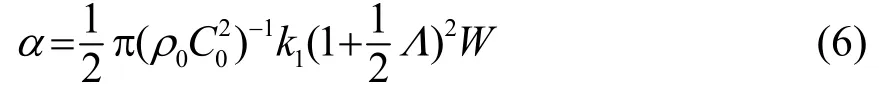
水介质的非线性转换效率低，这在参量阵的水声工程应用中一直是一个备受关注的问题。提高参量阵转换效率通常是从改变介质参数入手，如果介质的密度减小、声速减小、非线性参数增大，则非线性转换效率可显著增大。硅橡胶、气泡层作为提高转换效率的手段都获得了实验验证[14-15]。因为工程上很难在声呐前方产生足够大范围的高非线性效应介质，这种方法对于利用参量阵声纳进行水声探测的应用价值不大[16]，但对水下特定环境下降低低频辐射噪声或许有一定的效果。

虽然关于声散射声的争论还不能说有了确定的结论，但这对于非线性水声学的工程应用并没有太大影响。实际上参量阵和参量接收阵所关心的是声波相互作用区域范围内的声场，通常并不关心次级声源产生的辐射声问题。Westvelter 恰恰是在关于声散射声的争论过程中，在Lighthill 的建议下，发表了其著名的论文Parametric Acoustic Array[17]，建立了参量阵的基本概念和理论。也是在该文章的最后，提及了参量接收的概念（但没有用这个名称）。

2.2 参量接收阵

2.2.1 参量接收阵的基本原理

参量接收阵的基本原理是：用一个高频换能器发射一个频率为f0的高频强声波（称为泵波），使其与被接收的频率为fs（波长λs）的低频信号产生相互作用，由于泵波幅度很强，考虑声传播的非线性效应时，泵波与被测信号在相互作用区内会产生具有累加效应的差频波及和频波，参量接收阵原理示意图如图1 所示，其中L为泵波换能器到接收水听器的距离，称为参量接收阵的阵长，θ为被测低频信号传播方向与泵波-水听器连线之间的夹角。

图1 参量接收阵原理示意图 Fig.1 Schematic diagram of parametric receiving array

声散射声之所以会产生差频及和频波，从数学上理解是因为式（4）中Lighthill 方程的右边积分项（即所谓密度波的“虚源”）中出现了声压的平方项[17]，而声压又是两个不同频率声波的叠加，因此虚源中会出现两个不同频率声波的乘积，此即为产生差频波及和频波的虚源。

在 Westvelter 提出参量接收的概念之后，Berktay 最先对此进行了定量分析[18]。Berktay 最早的出发点是通过非线性效应获得的边带（差频及和频）信号应该比原来的低频信号强，即实现了所谓的参量放大。由于参量接收阵输出的边带信号幅度与其频率的平方成正比，要获得比原来的低频信号更强的边带信号，通常要求泵波频率足够高。而频率越高，则声吸收越大，接收到的边带信号会有更大的传播损失。并且，通常需要泵波在较长的距离上可近似为平面波，才能够获得足够大的参量放大系数。这些因素使得实际应用中实现边带信号比低频信号的幅度更大。因此，随后关于参量接收阵的研究更多的是其可以通过频率搬移，实现对低频信号的窄波束接收，而并非对弱信号的放大[19-23]。

由于参量接收阵是一个端射阵，因此其波束宽度与阵长密切相关。当被测信号为低频信号（几十至数千赫兹）时，往往要求参量接收阵的阵长达数十至数百米，才能实现窄波束接收。而这种情况下，泵波一般不再是平面波。Berktay 等推导出了泵波为球面波时参量接收阵输出的边带信号幅度及指向性公式[24]：

其中：ks=2 π/λs，P1是被测低频信号在接收换能器处的声压级，P2是泵波信号声源级。下标为±的变量表示和频和差频变量，ρ0和c0表示介质的密度和声速。参量接收阵在水平和垂直方向上都是指向性接收，从式（8）可知，参量接收阵的指向性类似于平面活塞换能器，是圆锥形波束。参量接收阵的空间增益即来自于其接收的空间指向性。

2.2.2 参量接收阵湖试测量试验

由于参量接收阵在水平和垂直方向上都形成了指向性，因此其在相对较短阵长情况下可获得更大的低频空间增益。阵增益DI满足公式[5]：

式中：L为参量接收阵阵长，λs为被测低频信号的波长。Richard 等通过湖试验证了参量接收阵可以获得式（9）所体现的很高的低频空间增益[25]。该试验的步骤为：

（1）校准参量接收阵的接收灵敏度。低频声源置于足够远处，使得声源发出的信号到达参量接收阵位置处可视为平面波。比较参量接收阵输出的差频信号和标准水听器输出的低频信号，获得参量接收阵的接收灵敏度。

（2）在没有低频发射信号的情况下，比较参量接收阵输出的差频信号，根据其灵敏度折算成低频信号的等效声压级，与标准水听器输出的低频信号（即环境噪声）比较，确定参量接收阵对环境噪声的抑制效果。

在文献[25]介绍的试验以前，绝大多数的参量接收阵试验都是在实验室进行的，并且主要是验证参量接收阵的接收指向性及输出差频及和频信号的声压级与理论计算的一致性，因此泵波和被测信号普遍采用的是频率相对较高的信号，并且被测信号的幅度都很大，以保证测量的准确性。但文献[25]中湖试测量的是低频环境噪声与泵波相互作用后的输出差频信号，被测信号幅度非常小，输出的边带噪声也非常小，差频信号比泵波信号幅度低150～160 dB。因此试验对泵波信号的频率稳定性和接收解调电路的自噪声特性要求非常高。该试验选取的泵波信号的频率为65 kHz，泵波声源的信号发生器输出信号在偏离载波频率400 Hz 处衰减了170 dB，偏离100 Hz 处衰减160 dB，频率稳定性非常高。

在参量接收阵中，两列声波相互作用本质上是相位调制[26-27]，泵波为纯单频信号时，有[25]：

其中：

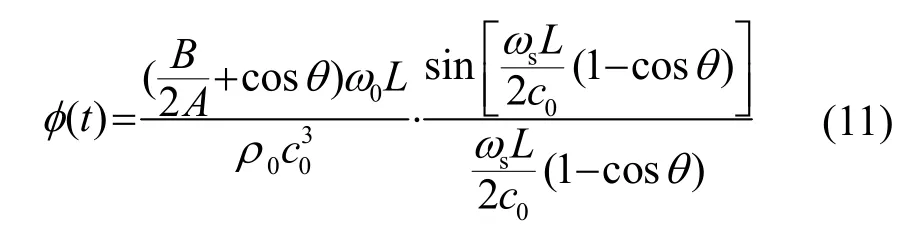
式（10）展开后的表达式为

由于调制相角ϕ(t) <<1，有：

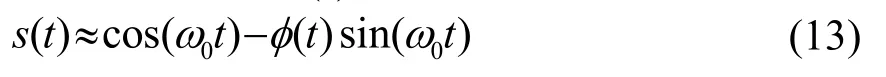
即相位调制与幅度调制基本上是等效的，参量接收阵的信号由泵波信号和抑制载波的双边带调幅信号组成，调制信号ϕ(t)即为参量接收阵的输出信号，式（11）显示其幅度和指向性与式（7）和式（8）是一致的。

该试验选择的参量接收阵泵波信号的频率为65 kHz，阵长L为340 m，对于频率为800 Hz 环境噪声的增益约为29 dB。对于频率为100 Hz 环境噪声的增益应该在20 dB 左右，但实际测得的增益也达30 dB。文章认为这是由于环境噪声在100 Hz 以下并非各向同性，而是存在一个与参量接收阵泵波信号传播方向相反的干扰源，而参量接收阵对这种反向干扰源有更强的抑制能力。

上海船舶电子设备研究所也开展了参量接收阵的湖试研究。湖试除了进行参量接收阵的低频空间增益试验外，还进行了模拟目标检测试验。湖试选择的泵波频率为100 kHz，声源级接近230 dB。选择参量接收阵的阵长约为200 m，重点测量对2 kHz 单频信号可实现的空间增益（由式（9）计算的理论阵增益约为30 dB）。与文献[25]中的试验略有不同，上海船舶电子设备研究所的试验增加了一个单频目标信号，通过直接测量接收该目标信号的信噪比变化来确定参量接收阵的阵增益。

图2 是标准水听器与参量接收阵检测频率为2 kHz 单频信号的比较结果。由于测试环境的本底噪声很低，试验中参量接收阵的信噪比增益实际上是受设备的自噪声限制。实际测得的信噪比增益约为25 dB，并没有实现对环境噪声抑制30 dB 的理论结果。

图2 参量接收阵与标准水听器输出信号比较 Fig.2 Comparison of output signals between the parametric receiving array and a standard hydrophone

试验还进行了对600 m 处模拟低速运动目标跨波束运动的探测，图3 是探测结果。图3 中模拟目标有三根线谱，频率分别为 1 950、2 000 和2 050 Hz。时间历程显示的是压缩后的目标穿过波束宽度为7°左右的参量接收阵波束的结果。

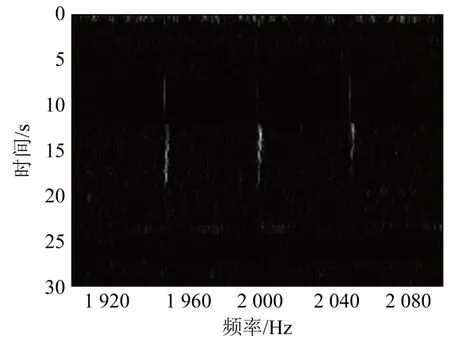
图3 参量接收阵对跨波束运动模拟目标检测结果 Fig.3 Detection result of simulated target cross-beam motion with parametric receiving array

2.2.3 参量接收阵应用于低频高增益接收的难点

由文献[25]和上海船舶电子设备研究所的试验结果可知，如果参量接收阵主要用于抑制低频环境 噪声，则要求阵长比较长，因此泵波声源一般只能是球面扩散声源；受限于水的弱非线性效应，泵波与被测低频声波相互作用所产生的边带信号往往比低频信号本身的幅度要小很多。从式（7）可以计算出当泵波源级为230 dB、频率为100 kHz、阵长为200 m 时，考虑海水对泵波的声吸收，输出的边带信号比低频信号低约25 dB。例如，对于强度为40 dB 的低频信号，其输出的边带信号强度仅为15 dB，而源级为230 dB 的泵波信号在考虑扩散衰减和声吸收后，强度为179 dB，因此“泵波-边带比”约为164 dB，即参量接收阵的接收端需要在强泵波干扰下检测极弱的边带信号。

另外，参量接收阵输出的是高频边带信号，还需要考虑高频环境噪声带来的影响。对于泵波频率为100 kHz、信号频率为2 kHz 的情况，边带频率下的环境噪声谱级比信号频率下的环境噪声谱级低约35 dB。如果接收换能器无指向性，则参量接收阵输出的信噪比增益仅为−25−（−35）=10 dB，要获得参量接收阵理论上30 dB 的增益，接收换能器还必须有20 dB 以上的高频空间增益。对于频率为100 kHz 左右的高频边带信号，采用平面阵接收相对比较容易实现此增益。

由于泵波信号远大于被测低频信号，因此边带信号与泵波信号的频率非常接近，如被测信号的频率为2 kHz，对于频率为100 kHz 的泵波信号则边带信号的频率为98 kHz 或102 kHz。对于源级为230 dB 的泵波和谱级为40 dB 的被测信号，泵波-边带比约164 dB，假设检测阈为6 dB，若要有效检测到边带信号，则要求泵波声源中所含有的边带频率噪声的谱级比中心频率谱级低170 dB，这对泵波声源的信号发生器和功率放大器的要求都极高。如果硬件能力难以满足该要求，则可考虑采用自干扰抵消的软、硬件结构设计，以在工程应用上实现参量接收阵对低频弱信号的高空间增益接收。

3 流散射声

流场对声传播的影响，是一个有很长研究历史的问题。海洋中最重要的，也是研究得最多的流场对声场的影响问题就是内波对声场的影响问题。对于内波对声传播影响的研究，主要是从内波区域的介质密度不均匀产生折射效应的角度开展的，而Lighthill 理论是基于造成介质不均匀的质点运动产生的应力效应的角度来进行分析，这二者是不同的思路。

Kraichnan 基于Lighthill 理论研究了湍流散射声波的问题[28]。从其研究结论来看，固然散射声场与流场的质点运动状态密切相关，但即使流场质点运动是单频简谐波，散射声场也是宽带声场，而不具备声散射声那种简单的单频调制效应。

Semenov 研究了潜艇运动产生的流场对声场的散射效应，并且声称基于此效应实现了对潜艇的超远程双基地主动探测[29]。其研究声散射的基本方程也是Lighthill 波动方程。本节主要对Semenov 的研究进行概略的介绍和初步的探讨[29]。

Semenov 的主要工作是基于其所描述的这样一个现象：潜艇在水下进行水平运动时，并不能完全保持深度不变，而是要通过操纵潜艇使其围绕某个深度不断周期性地上下调整深度，才能保持潜艇的稳定前行，只是深度调整的幅度很小，且周期很长（可达数百秒）。

由于潜艇这种周期性的低频运动，会导致潜艇本身产生极低频的左右摆动式的振动（不是类似于球面波声源的振动），如图4 所示。

图4 潜艇水下水平运动时的极低频摆动 Fig.4 The extremely low frequency swing of a submarine in underwater horizontal motion

振动频率满足Strouhal 关系：

其中：Ω为振动角频率，V和u分别是潜艇的体积和运动速度，Γ是量级为1 的常数，具体取值取决于潜艇的设计。对于排水量10 000 kg、航速10 kn的潜艇，Γ取0.1～0.2 时，振动频率为3.8～4.5 MHz（周期为260～220 s）。

文献[29]中认为，由于潜艇的振动，也会导致介质产生同频率的运动，即形成极低频率的重力波。该重力波的传播速度满足：

式中：c为重力波的传播速度，g为重力加速度，h为海深。式（15）是长波理论中的水波传播速度公式。Semenov 并未说明为什么潜艇这种极低频振动可以产生如此长的波长，以至于传播速度能满足长波理论。实际上Semenov 是先根据式（15）确定了重力波的传播速度，再反过来计算其波长，由此才计算出巨大的散射截面。由此自然也导致了不同海深时，潜艇振动产生的重力波的波长和传播速度也不同，所以才得出了海深h越大，重力波的散射截面也越大的结论。

Semenov 认为，由式（15）计算出这种重力波的传播速度远大于海洋自然环境中内波的传播速度，且不像形成常见的海洋内波那样需要环境中存在介质密度分层，因此这种重力波不仅对入射声波可以形成更大的散射截面，而且在任何有一定海深的海洋环境中都将由于潜艇的运动而出现。Semenov估算对于前述参数的潜艇运动，在海深200 m 时，其散射截面可达潜艇本身散射截面的200 倍，在深海时更大，因此即使其散射系数很小，也能够形成显著的散射效应。并且，其前向声波可以跟声散射声一样，形成明显的重力波对声波的调制效应。因此，Semenov 认为通过检测频率在毫赫兹量级的水重力波对声信号的调制效应，可以用于对潜艇的超远程探测。

基于上述理论，Semenov 还进行了实际的海上探测试验，声称在浅海环境下发射低频宽带声信号，潜艇运动造成的毫赫兹重力波对声波有显著的调制效应，检测到的调制深度可达20%；深海环境下更是可以达到40%。采用双基地探测模式时，通过对前向散射信号的检测、解调，可以探测到距离接收端300～500 km 之外的潜艇。

Semenov 的试验结果远远超出常规探潜技术的探测能力，因此引起了各方面的兴趣。不过到目前为止，我们还没有发现任何其他团队开展相关研究的文献资料，无论是理论的、还是实际海试的，都只能找到与Semenov 研究相关的文献。并且这本专著中关于这种新的超远程探潜方法的论述，仅有理论分析和实际海试探测潜艇的内容，中间没有提出可以对理论进行某种程度上的实验室或湖试验证的方法，这使得其他人如果要对此理论进行验证，并没有可供参考的低成本方式。而一般研究者也很难对真实潜艇进行海试探测，这应该也是造成我们很难找到其他研究者开展相关研究的参考文献的重要原因。

另外，仅从参考文献[29]来看，还有些不确定的理论问题。从该文献的4.3 节来看，作者似乎直接把潜艇的极低频振动（如果存在）当成一个中心位置不动的球面波振动源（尽管指出了多普勒效应可以忽略）。但实际上这种潜艇振动是在持续的水平和微弱的垂直运动中进行的，期间不断有潜艇运动的体积效应造成的流场扰动；并且对于运动中前后摆动的物体，其水下兴波也不是各向同性的[30]；这其中的关键因素可能还是在于式（15）对于由潜艇振动产生的重力波是否成立。再有，水下重力波的传播速度与声波的传播速度存在显著差异且声波及重力波传播方向不相同时，不能像参量接收阵一样实现同相累加。这种情况下流场仍然可以对入射声波的前向散射信号产生非常显著的单频调制效应，这也与Kraichnan 基于Lighthill 理论的研究结论[28]不同，值得进一步研究探讨。

4 结论

Lighthill 波动方程在已知流体应力分布的情况下可以获得简洁的积分解，对于研究介质扰动下的声传播效应有独特的优势。从Lighthill 方程出发，国内外学者对声散射声、参量接收阵等非线性声学问题进行了广泛、深入的研究。参量接收阵由于能以简单的配置形式实现低频高指向性接收，进而可以实现较高的低频接收增益，对于岸基低频声探测有较大的潜在应用价值。参量接收阵的应用难点在于自噪声的抑制，在硬件能力受限的情况下，需要考虑先进信号处理方法来实现。海洋中的流体运动也会对声传播产生影响。有报道认为由潜艇运动而产生的极低频海水重力波，可以用于双基地超远程探潜，对此还需要进一步的研究和观察。