圆周合成孔径声呐技术综述

杜选民，曾 赛

（1.上海船舶电子设备研究所，上海 201108；2.水声对抗技术重点实验室，上海 201108）

0 引言

合成孔径声呐（Synthetic Aperture Sonar,SAS）依靠小孔径基阵沿方位向移动形成虚拟的大孔径，对子阵获得的回波信号进行相干处理获得高分辨二维斜距面声图像[1-2]。SAS 图像的距离向分辨率与发射信号带宽有关，带宽越大，距离向分辨率越高；方位向分辨率与方位多普勒带宽相关，多普勒带宽越大，方位向分辨率越高。自20 世纪60 年代美国Raython 公司提出SAS 技术以来，经过半个多世纪的发展，SAS 技术已经逐渐发展成熟并走向工程应用，广泛用于水下沉底小目标的探测与识别。

由于水下沉底小目标具有尺度小、强度弱、散射不均匀、周围干扰目标多等特点，导致SAS 在水下沉底小目标的探测识别过程中仍然面临着漏警和虚警问题。首先，条带SAS 沿直线航迹扫测，这就使得声呐仅在有限的方位角范围内观测沉底小目标，仅能获取被测目标在部分方位或姿态下的回波信号，在一定的波束角条件下，合成孔径相干积累的距离或时间有限，限制了成像分辨率的进一步提高；其次，由于水下目标散射声场空间指向的不均匀性，在有限的观测角范围内存在探测不到目标的可能性，给条带SAS 图像的解释及目标识别带来困难；再者，目标深度或高度信息对于水下小目标的识别有重要价值，在条带SAS 基础上延伸出的干涉合成孔径技术虽然可以获得海底地形地貌的三维曲面高程图像，但并不是真正意义上的三维成像，即无法分辨相同距离-方位单元内不同高度的散射中心，并且由于干涉合成孔径体制需要采用两条接收阵，增加了系统的硬件复杂度和成本[3]。

圆周合成孔径声呐（Circular Synthetic Aperture Sonar,CSAS）[4]借鉴了圆迹合成孔径雷达[5-7]（Circular Synthetic Aperture Radar,CSAR）观测体制，基于圆形运动孔径测量水下目标回波数据，采用层析成像处理获得目标全孔径声学图像，是条带SAS 的一种改进。其基本原理是声呐在目标上方一定高度处，以被测目标或被测区域为中心按一定半径进行圆周运动；在运动过程中，声呐波束始终照射同一场景区域，同时获取被测目标或区域在不同方位角和掠射角下的回波数据；在数据处理阶段，沿高度向构建一系列断层，对每个断层分别进行层析成像[8-13]，从而获得二维成像图像序列，然后对序列图像进行相干叠加获得目标区域的三维图像。

CSAS 可以在多个方面弥补条带SAS 的不足[14]：（1）CSAS 对被测目标及环境的全角度回波进行相干成像，能够获得目标的三维声图像，降低了因目标散射声场各向异性、图像叠掩导致的漏警问题；（2）CSAS 最大化利用了测量孔径，能够获得更高成像分辨率；（3）CSAS 具备真正的三维成像能力，有利于提高对识别目标的置信度。

本文对国内外CSAS 成像技术的研究进展进行了概述，首先介绍了CSAS 成像的基本概念与分辨率特性，然后分析了国内外CSAS 试验研究进展，接着对CSAS 成像关键技术研究现状进行了分析，最后对CSAS 成像技术进行了总结与展望。

1 CSAS 基本原理

1.1 水声层析成像

CSAS 成像原理与医学层析[15]成像一致，其理论基础是空域傅里叶变换[16]，本质上是通过测量空间目标图像的波数谱或空间频率谱（与目标图像互为傅里叶变换对）数据实现成像。根据傅里叶变换的性质，成像分辨率由波数谱或空间频率谱数据获取范围确定，范围越大，分辨率越高。水声层析成像原理简述如下：首先，假设被测目标分布在二维平面内，建立水声层析成像测量的目标回波信号模型，如图1 所示，以被测成像空间区域的中心O为 原点建立平面直角坐标系xOy，声呐到被测区域中心的距离为R0，声波入射方向与x轴的夹角为θ，即声呐运动方位角。

图1 CSAS 层析成像原理 Fig.1 Principle of CSAS imaging

当声呐与被测目标之间的距离满足远场条件时，采用平面波近似，声呐在θ方位角采集的回波信号可以表述为：

其中：p0(t)是声呐主动发射信号；c是水中声速；q（x,y）为目标外形及其内部结构特征反射特性图像分布，它的物理意义是能产生几何亮点的目标外形轮廓及内部强回声结构的空间分布。在式（1）中，相对延迟距离s是散射点矢量r（x,y）沿θ方向的投影距离，s=xcosθ+ysinθ。对pθ(t)进行一维傅里叶变换，可以得到：

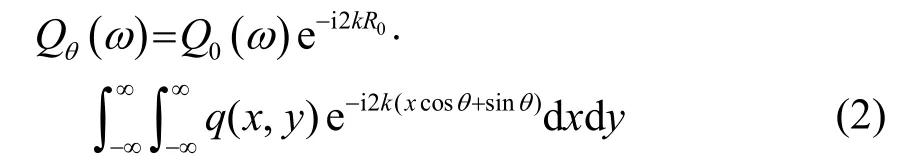
其中：Q0(ω)为主动发射信号频率谱；波数k=ω/c。

对q（x,y）进行二维傅里叶变换，可以得到空间频率谱：

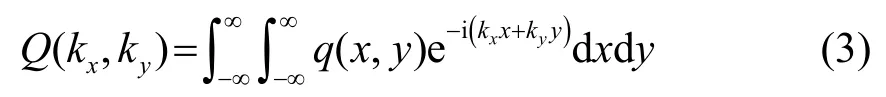
令kx=2kcosθ、ky=2ksinθ，代入式（3），并与式（2）比较，可以得到：

式（4）建立了时域回波信号pθ(t)的一维频率谱与被测目标或被测区域反射特性图像q（x,y）的二维空间波数谱之间的数学关系，从而可以获得全方位角的空间频率谱。回波信号谱与二维空间谱之间的关系如图2 所示。

图2 回波信号谱与二维空间谱之间的关系 Fig.2 Relation between echo signal spectrum and 2D spatial spectrum

如果声呐沿部分圆周进行测量，从方位角θ1运动到方位角θ2，则被测目标或被测区域的空间谱数据分布如图2 中的扇形圆环部分。通过二维傅里叶反变换可以得到被测目标或被测区域成像结果，即：

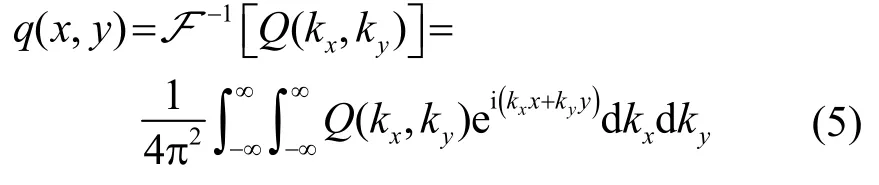
1.2 CSAS 分辨率分析

条带SAS 方位向和距离向的成像分辨率分别为[17]

其中：R0为声呐到被测目标的距离，λ为中心频率对应的波长；B为信号带宽；Lsa为合成孔径长度。

将合成孔径角θsa≈ 2asin (Lsa/2/R0)代入式（6），则有δ x=λ/ [4 sin (θsa/2)]，方位向分辨率决定于观测方位角范围，通过增大观测方位角，可以提高分辨率。若θsa=π，则δ x=λ/4，即在理论上，水声层析成像的方位向分辨率可以达到亚波长量级。

点扩散函数能够描述声呐的成像性能，通过公式推导可以得到CSAS 的点扩散函数[18]：

由式（8）可以看出，基于圆形运动轨迹的水声层析成像系统方位向的分辨率在窄带条件下取决于工作频率，宽带条件下取决于工作带宽，并与距离向的分辨率相当。

2 典型CSAS 试验研究进展

CSAS 的概念源于CSAR，一经提出，便引起多国研究机构的关注。从CSAS 成像原理分析到CSAS 试验研究，国内外研究机构做了大量的研究工作。

2.1 国外研究进展

Soumekh[5]于20 世纪90 年代首次提出了CSAR基本信号模型，标志着CSAR 研究的开端。此后,多国水下机构开展了CSAS 的原理试验。

1995 年，澳大利亚国防研究机构宾克利夫斯（Defence Research Agency Bincleaves,ARAB）采用圆形测量轨迹，利用计算机断层扫描（Computed Tomography,CT）成像原理对水中的石块以及圆柱目标进行了二维成像。2001 年，澳大利亚汤姆森马可尼声呐公司为澳大利亚海军开发了水雷声成像声呐原型样机AMI，旨在帮助澳大利亚海军在浑浊水域识别水雷目标，在该原型样机中，采用了圆轨迹测量模式，对圆柱形水雷目标进行了二维成像。2005 年，澳大利亚国防科技组织（Defence Science and Technology Organization,DSTO）开展了水下目标圆迹层析成像理论和试验研究[19]，利用傅里叶中心切片定理，该组织成员对实测的水声数据进行了二维成像，试验中采用高频150 kHz 和低频40 kHz的频率在自由场条件下对Manta 水雷各个姿态角下的回波数据进行采集。试验用Manta 水雷如图3 所示，其尺寸为：顶部与底部直径分别为 49 和98 cm，高为47 cm。成像处理后得到的结果如图4所示。此后，DSTO 开展了对沉底Manta 水雷的CSAS 成像试验，并取得了较好的成像效果。

图3 试验用Manta 水雷 Fig.3 Manta mine used in trail

图4 两个不同频率的Manta 水雷成像 Fig.4 Manta mine imaging with two different frequencies

2006 年，美国海军研究局（Office of Naval Research,ONR）支持开展了基于无人水下航行器（Un-manned Undersea Vehicle,UUV）平台的CSAS 原理样机研究，该项目进行了湖上沉底目标成像试验，采用主动声信标用于运动误差补偿[20]，试验取得较好的成像结果。2011 年，美国海军水面战中心（Naval Surface Warfare Center,NSWC）支持Marston 等开展有限孔径的圆合成孔径数据处理研究[21]；2013 年，为深入开展CSAS 成像算法和补偿算法研究，NSWC 专门建造了试验水池以及水下圆形导轨用于实验的测量[22]，获得了沉底水雷和掩埋雷的二维成像结果。2014～2016 年，美国海军研究局（ONR）持续支持华盛顿大学应用物理实验室开展CSAS 项目研究，项目组采用REMUS 600 UUV 搭载小型合成孔径猎雷声呐（Small Synthetic Aperture Minehunter，SSAM）沿不同高度做圆周测量或螺旋线测量，获得了典型水下目标的三维图像[23]，效果非常好，图5 为“梯子”目标和自行车目标的成像结果。通过对美国在CSAS 领域中的研究现状分析可知，其在CSAS 领域处于国际领先地位。

图5 水下实验目标及其三维成像结果 Fig.5 Underwater experimental targets and their 3D imaging results

2008 年，挪威国防研究机构（Norwegian Defense Research Establishment,NDRE）支持开展基于HUGIN1000 UUV 平台的单航次层析成像试验[24]与运动补偿研究，相关研究结果在国际会议上以摘要形式发表[25]。

2016 年，加拿大研究机构利用Kraken 海洋机器人系统搭载AquaPix Multispectral 合成孔径声呐，开展了CSAS 原理研究[26]。其在水池中利用旋转平台对铝制圆柱目标进行了二维成像研究，并根据圆迹回波的角度频率谱分析了铝制目标的弹性特征。

2014 年，印度海军物理与海洋测绘实验室展开水下目标声层析重建研究，对回波采用后向投影重建，得到了较为精确的目标外形轮廓[27]。

2.2 国内研究进展

国内开展CSAR 成像技术研究的单位众多[28-41]，而开展CSAS 成像技术研究的单位较少。从2016年开始，上海船舶电子设备研究所在国内率先开展CSAS 成像技术的理论研究与试验验证工作[3-4]，已完成了原理样机的研制，突破了一系列关键技术，正在开展工程应用研究。通过水池试验对CSAS 的成像原理进行了验证。如图6 所示为Benchmark 潜艇目标的二维成像结果，从中可以看出，潜艇模型的指挥台、肋板以及外形结构均得到了重建，并且与真实的结构一致。图7 为立体架目标的三维成像结果，通过三维层析成像处理，能够精确反演得到三维小球模型的三维立体像结构，每层小球个数与实际模型吻合，而且小球间距与实际吻合。项目组开展了湖上试验，获得了水底目标的二维和三维图像，如图8 和图9 所示。

图6 Benchmark 目标模型二维成像结果 Fig.6 Two dimensional imaging result of Benchmark model

图7 水下立体架及其成像结果 Fig.7 The underwater 3D frame and its imaging result

图8 湖上试验的沉底目标及其二维成像结果 Fig.8 Bottom target in lake trial and its 2D imaging result

图9 湖上试验沉底目标的三维成像结果 Fig.9 Bottom target in lake trial and its 3D imaging result

3 CSAS 关键技术

国内外的多次试验已经证实了CSAS 成像效果的优异性，但其优势是建立在复杂的硬件系统和算法之上。下面从成像算法、运动补偿、三维成像与后置处理4 个方面对CSAS 成像技术的现状进行分析。

3.1 成像算法

由于CSAS 采用的是特殊的曲线孔径，导致基于直线孔径的条带合成孔径声呐的成像算法[42-47]（距离-多普勒算法、C-S 算法、ω-k算法）不再适用于CSAS 成像。

CSAS 成像一般分为两大类，一类是时域法[2-4]，代表性的时域算法有后向反投影（Back Projection,BP）算法、滤波反投影（Filter Back Projection,FBP）算法、因式分解快速后向投影（Fast Factorized Back Projection,FFBP）算法、互相关法和共焦成像算法等；另一类是频域法[40,48]，代表性的频域算法有极坐标算法[49]、傅里叶重建算法和基于子孔径的频域算法[50-53]。

时域成像算法中，BP/FBP 算法由于成像精度高、成像模式简单、运动补偿容易、无运动轨迹限制等优点而成为CSAS 常用的成像算法。但由于CSAS 的成像孔径远大于SAS 的成像孔径，使得回波数据量较大，基于BP/FBP 算法的CSAS 成像存在计算量大、成像效率低的缺点。因此，BP/FBP算法通常用于衡量CSAS 其他算法的性能。

为了解决BP/FBP 算法计算量大、成像效率低的问题，学术界通常从两个方面开展研究。（1）通过硬件并行化处理提高BP/FBP 计算效率，如利用图形处理器（Graphics Processing Unit,GPU）[54]结合BP 算法，能显著提高CSAS 成像效率，其缺点在于提升了硬件成本。（2）改进BP 算法，较为成功的是FFBP 算法。FFBP 算法的核心思想是牺牲部分图像分辨率达到提升计算效率的目的，其通过对圆形孔径进行子孔径分解达到计算效率提升的目的，但FFBP 算法需要对子图像进行插值，会引入插值误差，孔径的划分会影响插值误差，且误差会不断累积放大，最终影响成像质量。对数据进行频域处理是提升CSAS 成像计算效率的有效途径，其中典型的算法是傅里叶中心切片定理（Fourier Slice Theorem,FST）。FST 算法通过对回波数据进行波数域插值后完成对二维图像的重建，大大提升了计算效率。此外，极坐标算法亦是计算效率较高的频域算法。FST 算法的缺点是只能对观测场景中心及其较小的邻域场景进行高效成像，随着观测场景的增加，算法对内存需求急剧增加、插值运算误差放大导致成像分辨率下降。非均匀快速傅里叶变换（Nonuniform Fast Fourier Transform,NUFFT）算法[53]通过对全体回波数据插值替换FST 算法的内插方法，从而减小了插值误差，提升了成像效率，但成像结果会有主瓣展宽、旁瓣升高的缺点。

CSAS 的点扩散函数特性表明其二维成像具有高旁瓣的特点，旁瓣形状为环状，通过加窗[33]、低通滤波均无法抑制或降低旁瓣，反而牺牲了成像分辨率和信号相位，导致聚焦失败。基于Lp范数[55]图像特征增强的CSAR 成像方法为降低CSAS 二维图像旁瓣提供了思路，该方法将成像问题转化为最优化求解问题，降低了旁瓣，但会导致主瓣展宽，影响成像精度。

3.2 运动补偿算法

CSAS 运动平台在观测过程中易受到水流的影响而偏离理想运动轨迹[56]，从而产生运动误差。从运动误差的特征来看，可以分为平动（纵荡、横荡、垂荡）误差和转动（纵摇、横摇、横滚）误差两大类[57]。平动误差会导致声呐基阵相位中心偏离理想运动轨迹，产生距离单元徙动（Range Cell Migration,RCM），从而使相位误差增大，严重影响成像质量；转动误差会导致声呐发射阵波束脚印偏离目标场景区域中心，当波束脚印较窄时，易导致目标场景偏出声呐辐射范围，无法获取目标有效回波。转动误差通常可以通过宽波束发射或运动云台控制来补偿，平动误差则必须进行传感器数据修正或回波数据补偿。

相比于条带SAS，CSAS 运动误差呈现出新的特征，一是合成孔径增大，且孔径为曲线，更易形成误差；二是误差呈现严重的二维空变性[58]，即场景中的每个目标遭受的运动误差各不相同，难以进行统一补偿，而条带合成孔径误差可以分为方位向误差和距离向误差分别进行补偿。

CSAS 的运动误差特性导致对其进行图像聚焦具有很大的挑战性。其成图所需的相干积分孔径比同范围的线性扫描积分孔径大一个数量级，圆形积分孔径的高度非线性导致聚焦依赖于水中散射体的高度，在图像自动对焦问题中，这种特性会导致导航误差与目标真实位置之间的强耦合。除了运动误差会导致图像聚焦模糊之外，水体声速非均匀也会导致成图模糊[59-60]。

针对CSAS 运动误差的补偿方式主要有两种：（1）基于运动传感器进行误差粗补偿[57,60-62]，如利用惯性导航系统（Inertial Navigation System,INS）或惯性测量单元（Inertial Measurement Unit,IMU）、多普勒测速仪（Doppler Velocity Log,DVL）和GPS 对运动平台信息进行感知后修正运动偏航，基于运动传感器的补偿方法的补偿精度取决于传感器性能，其通常无法修正亚波长级别的运动误差，但其优点是实时性好，处理过程相对简单，能够完成对场景的粗略成像。（2）基于声呐回波数据的运动补偿[63-74]，其基本原理是运动误差必然藏在回波结构中，该方法能够补偿亚波长级别的误差，实现对目标的精确成像，补偿精度高，适用性好，其缺点是处理过程繁琐。根据使用回波的形式可以将基于回波信号的补偿方法分为“微导航”和自聚焦两类。“微导航”方法使用原始信号估计载体的运动信息，如偏移相位中心法（Displaced Phase Center,DPC）。自聚焦方法使用回波图像域数据进行相位补偿，如相位梯度自聚焦（Phase Gradient Autofocus,PGA）方法和偏移帧图像自聚焦（Displace Frame Image Autofocus,DFIA）方法。

针对运动传感器测量精度无法满足亚波长运动补偿需求的问题，在早期CSAS 试验过程中，国外研究机构通过在场景中布置主动声信标或水听器进行载体运动轨迹重建[20]，计算运动误差引入的相位误差，补偿原始信号回波，实现亚波长导航精度，从而完成对目标的精确二维成像。该方法一般用于成像算法验证，缺点是实用性较差，因为在真实的工作场景下，往往不允许在成像场景中布设合作信标。值得指出的是，早期的CSAR 试验依赖于成像场景中的各向同性散射体（非合作信标）来完成运动补偿[59]。其原理与合作信标有所区别，CSAR依赖各向同性散射体补偿的本质是在小的观测场景半径、扫描半径比下点扩展函数（Point Spread Function,PSF）在图像上近似均匀，而CSAS 的场景半径、扫描半径比较大，像差孔径方差（Aberration Spatial Variance,ASV）很大导致点扩展函数非均匀。值得注意的是，CSAS 场景半径与扫描半径较大的原因在于观测目标位置不确定与载体导航积分漂移共同导致的[60]。

为了摆脱对观测场景中主动信标的依赖，采用子孔径半相关方法进行CSAS 运动补偿[75-76]，其本质是通过谱相关对子孔径图像之间的最优平移量进行估计，从而实现图像对焦。该算法的缺点在于，其要求信号的相位一致性较好，且限于处理点目标，在远离点目标的区域，图像质量会迅速下降。

为了解决CSAS 图像中像差空间变异的问题，研究人员提出了一种利用局部二次相位误差来估计运动误差并进行校正的方法[77]，该方法使用一对一维方位滤波器生成斜视“伪条带”图[21,78-79]，在此基础上，估计二次相位误差的距离和角度的相关性并将其分解为导航误差进行校正。由于斜视“伪条带”图是二维的，对于三维运动误差估计，因此该方法是欠定的。

为了同时解决对主动信标的依赖以及运动误差导致空间畸变而引起的图像像差问题，Cantalloube[80]提出了一种鲁棒的圆周合成孔径数据聚焦方法，即多点定位（Multilateration,MLAT）法。该方法利用多子孔径相关技术对成像场景中的子图像块单独聚焦，通过生成微导航方案，完成对斜距误差的估计。由于没有考虑导航误差与聚焦平面（高度）误差之间的强耦合关系，特定条件下该方法补偿失效。

事实上，Callow 等已经指出运动平台的导航误差与聚焦平面误差都会导致CSAS 图像散焦[76]，二者高度耦合，在进行运动估计时必须同时给出导航误差估计值与散射体高度值（聚焦平面高度）。Ran等在条带扫描数据聚焦处理中[81]，基于多点定位理论，通过加 权总最 小二乘（Weighted Total-Least-Squares,WTLS）方法同时估计了导航误差和子图像位置，为CSAS 图像聚焦处理提供了参考。

现有MLAT 算法基于的是子孔径相关技术。由于子孔径相关技术强烈依赖于图像的目标-杂波比，当场景中存在极端各向异性散射体、目标-杂波比很低或者波束在某些角度未覆盖目标时，基于子孔径相关的参数估计模型会由于这些异常值的影响而导致误差估计失败，从而导致多点定位方法失效。为了降低多点定位算法对异常值的敏感性，Marston 等[60,82]通过引入正则化项，对噪声解区域进行隔离和平滑插值处理，采用数据加权的正则化高斯-牛顿（Guass-Newton,G-N）方法求解全局非线性超定方程，同时给出了导航误差和聚焦平面误差，实现了图像聚焦。此外，Marston 等[83]还针对子图像相位误差估计，提出了波数域广义锥模型，较好地对图像进行了相位补偿，实现了图像聚焦。

3.3 三维成像

单航过CSAS 波数谱支撑域为圆台或倾斜圆台三维结构，波数谱三维结构表明单航过CSAS 具备三维成像能力[3]。文献[4]通过改变聚焦平面，仿真与试验验证了单航过CSAS 的三维成像能力。此外，基于投影共焦三维成像算法以及最小能量准则参数估计的三维成像算法在单航过CSAR 中得到了验证，为单航过CSAS 成像提供了依据。

为提升CSAS 三维成像的高度向分辨率，研究人员提出并试验验证了CSAS 多航过观测模式。典型的多航过（Multi-Pass）模式分为三种：径向多航过、高度向多航过和沿着高度向的螺旋上升式多航过。多航过模式增加了高度维的合成孔径长度，通过垂直维高分辨算法实现高度维的高分辨，最终实现CSAS 的高分辨三维成像，文献[23]、[83-85]也表明，压缩感知（Compressed Sensing,CS）算法是抑制CSAS 高旁瓣、高度维高分辨率和三维成像的理想技术途径。

水下航行器绕观测目标进行多航过测量，会导致测绘时间较长、不同航过数据难以对齐等问题，而且由于运动载体容易受到水文环境的影响，多航过测量时会形成运动平台累积误差，这会对多航过CSAS 三维成像的运动补偿形成巨大挑战。为了解决该问题，文献[3]通过利用垂直短阵进行单航过测量，一次性解决了多航过测绘时间长、数据对齐难的问题，对高度向数据进行高分辨阵列处理，对水平向数据进行二维层析处理，对不同高度向数据进行相干处理获得了水下目标三维图像。垂直短阵测量模式的缺点是工程使用受限。

此外，CSAS 三维成像图像的渲染、表征与快速显示[82]也是值得研究的课题。

3.4 后置处理

随着人工智能技术的发展，许多机器学习和深度学习方法已经应用于前视声呐、侧扫声呐和合成孔径声呐图像的后置处理，如目标的自动检测、图像分割、特征提取与识别[86-95]等，并取得了较好的处理效果。

与传统的声呐图像相比，CSAS 图像分辨率更高，具备三维特征，信息量更加丰富。在光学图像处理领域获得成功的深度学习方法在CSAS 图像后置处理方面具有广阔的应用前景[96-97]。2020 年，美国海军海上系统司令部（Naval Sea Systems Command）机器智能防御实验室（Machine Intelligence Defense Lab）采用半监督深度卷积自编码-解码网络对CSAS 声呐图像进行了目标检测、分割和识别处理[98]，其基本思路是采用单支编码（Single-Branch-Encoding,SBE）、多支解码（Multi-Branch-Decoding,MBD）卷积网络实现对CSAS 图像目标的检测、跟踪和分割，编码器分支从CSAS 图像中提取不同空间尺度的对比特征，一支解码器分支以无监督方式突出显示视觉域显著区域，其他解码器分支通过监督学习细节标记图像的前景和背景，将候选分割解决方案输入深度解析网络，得到最终目标的轮廓，完成目标分割和特征提取，实现目标自动识别。结果显示，该深度学习方法在其CSAS 图像数据集上取得了显著的分割与识别效果。

4 CSAS 存在的问题和发展趋势

4.1 存在的问题

本文对CSAS 系统和试验的研究进展进行了综述，详细分析了其关键技术的发展现状，对比国内外研究现状，CSAS 技术尚存以下问题：

（1）成像算法有待进一步优化。时域成像精度高但效率低，频域成像算法计算效率高但算法复杂实时性较差。因此，亟待发展适合硬件并行处理的快速时域成像方法。此外，旁瓣抑制也是需要考虑的问题。

（2）运动补偿方法有待进一步改进。运动补偿是合成孔径声呐成像处理永恒的主题，CSAS 由于曲线孔径引起的导航误差与聚焦平面误差高度耦合，尚不存在鲁棒性的运动估计补偿算法，需要在该方向持续研究[99]。

（3）三维成像技术有待优化。CSAS 多航过测量方式导致高度维采样稀疏非均匀且航过次数有限的情况下，高度维的分辨率将更多地依赖于阵列信号处理，由于高程采样是时变的，需要考虑高程数据的对齐问题。如何用最少的航过次数实现高精度三维成像也是需要考虑的问题。此外，三维图像的快速显示与表征、基于方位角的图像显示也是值得研究的课题。

4.2 发展趋势

从二维成像拓展到三维成像是SAS 成像技术的一次重要跨越。CSAS 三维成像解决了常规SAS中的成像叠掩问题，能够实现目标的三维分辨，从而可以在复杂场景下对目标进行三维定位、获取垂直结构等。未来CSAS 三维成像技术结合UUV 平台技术，能够大大提高对水下小目标探测识别的工作效率，尤其是可以采用分阶段搜索的方法。在目标搜索阶段，利用前视声呐、侧扫声呐、合成孔径声呐等多种成像模式远距离发现目标；在目标查证阶段，利用声呐层析成像获取目标的全方位精细图像。

5 结论

由于CSAS 具有亚波长量级的二维平面分辨率、三维成像能力以及全方位观测能力等优势而得到广泛关注。本文分析了CSAS 成像原理和分辨率特征，详述了CSAS 国内外研究和试验进展，从成像算法、运动补偿、三维成像和后置处理等4 个方面综述了CSAS 关键技术的研究进展，分析了其存在的问题和发展趋势。随着电子技术和信号处理技术的迅猛发展，CSAS 技术将得到进一步发展，并走向工程应用。