等效阻尼比模型对高桩码头地震位移需求的影响分析*

高树飞，冯云芬，贡金鑫

(1.聊城大学 建筑工程学院，山东 聊城 252000；2.大连理工大学，海岸和近海工程国家重点实验室，辽宁 大连 116024)

由于基于位移的抗震设计方法相比于传统基于力的抗震设计方法具备诸多优点，已为国外多个高桩码头抗震设计规范和标准所采用，此方法中准确合理地确定地震作用下码头上部结构的最大水平弹塑性位移反应(地震位移需求)是关键[1-4]。由于强震作用下，码头结构会进入弹塑性状态，地震反应分析须考虑材料非线性。一般而言，对于给定的地震动时程记录，非线性时程分析可较为准确地计算结构的整体位移和局部变形，此方法也被公认为是最准确的抗震分析方法。但是，非线性时程分析复杂且计算量大，在分析时须选取多条地震动时程记录，而抗震设计一般是基于设计反应谱而不是地震动时程。因此，基于位移的抗震设计方法需要一种简便且具有足够精度的位移需求分析方法，相关规范和标准[5-7]常用的是替代结构法，该方法是等效线性化方法的一种，此类方法的基本假定是单自由度体系的最大弹塑性位移可由一个周期和阻尼比较原体系更大的线弹性体系的弹性位移确定，此方法需要确定等效线弹性体系的等效周期和等效阻尼比，故不同等效线性化方法的差别在于等效周期和等效阻尼比的计算方法，一般而言等效周期均是基于结构的割线刚度确定，而阻尼比则由相关的计算模型确定，因而阻尼比是替代结构法的关键参数，高树飞等[8]的研究结果表明其取值对于位移需求有至关重要的影响。

等效阻尼比被用来表征非线性结构体系能量耗散，已有学者针对不同结构类型提出了很多计算模型[9]。对于高桩码头而言，长滩港码头设计标准(WharfDesignCriteria)采用的阻尼比计算公式是基于建筑结构框架得出的，美国土木工程师协会标准ASCE/COPRI 61-14采用的计算公式是基于修正Takeda滞回模型推导得到的，而Takeda滞回模型是基于普通钢筋混凝土柱拟静力试验提出的。针对码头设计规范和标准采用的阻尼比计算式并非是基于码头结构特点而提出这一问题，文献[10]和[11]提出了两组计算公式，并各自做了简单验证。但是，等效阻尼比对于码头位移需求的影响仍缺少定量分析，在抗震设计如何考虑这一影响有待研究。

本文为分析等效阻尼比计算模型对码头位移需求的影响，选取一定数量的地震动记录，同时采用替代结构法和非线性时程分析方法对码头进行位移需求分析。考虑到非线性时程分析的准确性，将时程分析结果视为位移需求的准确值，计算两种方法所得位移之比，对位移比开展统计分析，并基于分析结果评估阻尼比计算模型的影响，并给出相关的建议，以供抗震设计参考。

1 替代结构法基本原理

非线性动力时程分析计算量大且收敛困难，当获取的反应是结构整体最大位移而不是局部变形时，非线性静力需求分析则较为简便。非线性静力需求分析方法有两大类：一类是前文提及的等效线性化方法，替代结构法和建筑结构中常用的能力谱法均属于此类，只是能力谱法可用于多自由度体系，而替代结构法只能用于单自由度体系，对于码头则是求解码头横向位移反应Δt，即求解一个排架或断面[12]；另一类则是位移系数法，该法认为单自由度体系的最大弹塑性位移可通过将相应弹性体系的最大弹性位移乘以一个系数确定，该系数为最大弹塑性位移与最大弹性位移之比，即非弹性位移比，此法可参考文献[13]。在进行非线性静力需求分析时须将原结构等效为单自由度体系，对于一般的梁板式码头而言，码头质量主要集中于上部结构，故直接将码头视为单自由度体系，不必再利用振型(一般是第一振型)将其等效为单自由度体系，但对于多层系缆的框架码头，等效过程不可或缺，此时可使用能力谱法，而不是替代结构法。

图1 码头推覆分析

使用替代结构法时，按以下分析步骤进行：1)建立码头数值分析模型，一般采用非线性Winkler地基上的梁模型进行建模，再对码头进行推覆分析，即对码头上部结构施加逐级递增的水平荷载，见图1a)，得到水平荷载F和上部结构水平位移Δ的关系曲线，即Pushover曲线；2)由于待求的码头横向位移需求Δt未知，可先假定一个初始值，再对Pushover曲线进行折线化处理，得到码头的割线刚度Ke、延性系数μ=Δt/Δy以及屈服后刚度比r等参数，见图1b)，分析中码头初始刚度K可取曲线原点至曲线上桩基首个塑性铰出现时对应点连线的斜率；3)计算码头地震质量m，ASCE/COPRI 61-14规定m考虑上部结构质量以及作用在上部结构上外荷载的换算质量，同时还包括桩顶至岸坡坡面以下5倍桩径范围内桩基质量的1/3；4)采用前述参数计算码头割线周期T和等效阻尼比ξeq；5)利用T和ξeq从设计加速度反应谱上得到相应的谱加速度值Sa；6)计算新的位移需求，如果计算值和初始值的误差在可接受的范围则停止，否则迭代计算直到精度满足需要。替代结构法的分析流程，见图2。

图2 替代结构法计算流程

2 等效阻尼比模型

从替代结构法计算流程不难看出，等效阻尼比是该方法的关键参数。等效阻尼比包含弹性阻尼比和滞回阻尼比两部分，弹性阻尼比表征结构体系在弹性范围内的耗能，一般取固定的数值，而滞回阻尼比则表征结构进入非线性状态后的滞回耗能。不同码头规范和标准采用的等效阻尼比ξeq计算模型并不相同，主要差异在滞回阻尼部分，长滩港码头设计标准采用的计算公式为：

ξeq=0.10+0.565[(μ-1)/(μπ)]

(1)

ASCE/COPRI 61-14采用的公式为：

(2)

由于式(1)(2)非针对码头结构特点提出的公式，文献[10]考虑将码头的滞回阻尼耗能分为桩塑性铰耗能EDp和土弹簧耗能EDs两部分，由此推导出的计算公式为：

(3)

针对式(3)存在的问题，文献[11]通过开展码头拟静力数值试验分析其滞回特性，进而提出对混凝土桩码头采用Pivot滞回模型[14]表征其滞回特点，由此基于该滞回模型推导出阻尼比计算公式：

(4)

其中：ψ=1+r1μ-r1

(5)

ψ′=1+r1μpk-r1-r2μ+r2μpk

(6)

β′=[1-(r2μ-r2μpk)/(1+r1μ-r1)]β

(7)

式中：r1为强化段刚度比；r2为下降段刚度比；α和β为滞回模型参数，取值参考文献[11]；μpk为峰值承载力Fpk对应的延性系数。由于Pivot模型使用带下降段的骨架曲线，故在使用式(4)时，当Δt超过Fpk对应的位移Δpk时，须对实际Pushover曲线进行三折线化处理，见图3，否则按图1b)处理即可。另外，初始刚度K的计算方法与式(1)(2)相同。

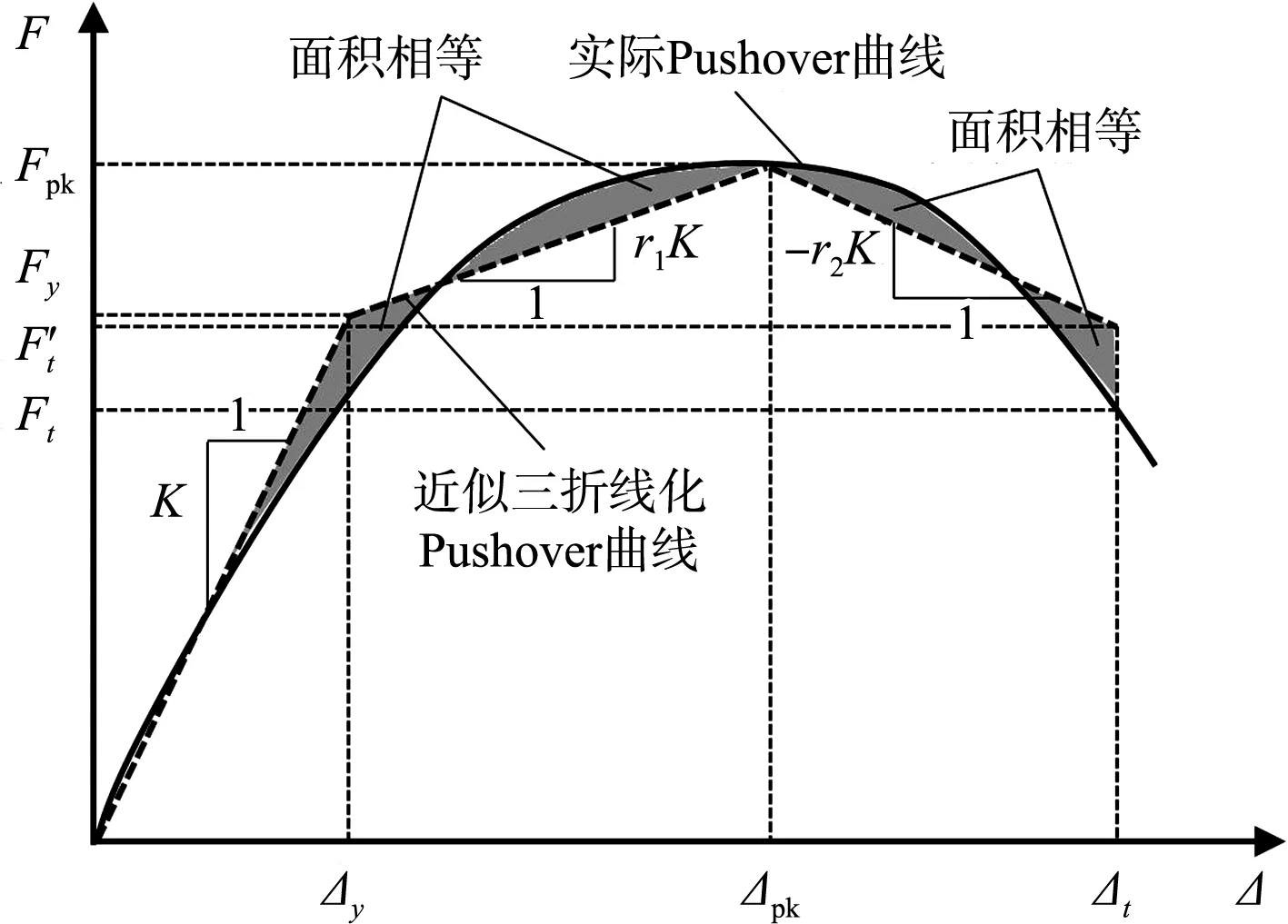
图3 Pushover曲线三折线化处理

对于钢管桩码头，文献[11]则提出采用Masing准则刻画其滞回特性，进而提出相应的阻尼比计算式：

(8)

Ft′=bF1ln[a(Δt/Δ1)+1]

(9)

式中：Δ1、F1分别为首个桩塑性铰出现时上部结构水平位移、荷载；a、b为参数，按文献[11]确定。使用式(5)时，无需对Pushover曲线进行任何处理。

3 影响分析

3.1 分析流程

(10)

(11)

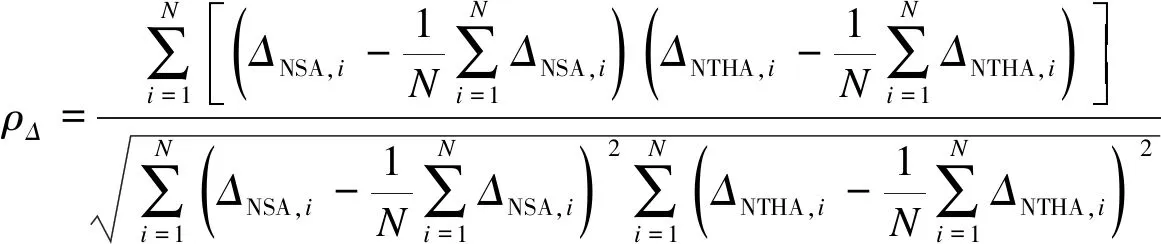
(12)

3.2 地震波

一般而言，当地震波数目超过20条时，时程分析结果就具备足够的统计意义，同时考虑计算量，故本文将地震波数目N取60。地震波从美国大平洋地震工程研究中心的数据库中选取，选中的地震波同时满足以下条件：1)峰值地面加速度PGA>0.2g；2)场地等效剪切波速大于180 m/s。限于篇幅，有关地震波的信息不再列出。另外，计算每一条波在不同阻尼比(0.05～0.35)下的弹性加速度反应谱，其中5%阻尼比下所有地震波的反应谱见图4a)，图中每条灰色曲线代表一条波的反应谱，不难看出不同波的反应谱差别极大；某条波在不同阻尼比下的反应谱见图4b)，限于线条种类，图中仅给出阻尼比取7个值时的结果，可看出阻尼比越大，加速度反应越小。

3.3 案例概况及建模

某码头断面见图5，排架间距6.30 m，轨道梁宽度是1.6 m，除此之外的纵梁和横梁的宽度均是1.5 m，码头面堆载是40 kN/m2。由于上部结构刚度和强度相比于桩基大得多，强震下梁板一般不会进入非线性，故结构非线性耗能主要集中于桩基，而不同桩基耗能能力不同。另外，不同土体耗能能力不同，为降低模型复杂程度，考虑岸坡为单一土体。为反映上述影响，考虑3种桩基和土体类型组合，分别为案例1～3。其中案例1的桩基为混凝土灌注桩，直径800 mm，纵筋配筋率1.25%，土体是内摩擦角为38°的粗砂；案例2的桩基为PHC管桩，直径1 200 mm，纵筋配筋率0.87%，土体是内摩擦角为34°的粗砂；案例3的桩基为钢管桩，直径800 mm，壁厚10 mm，土体是内摩擦角为30°的中砂。限于篇幅，桩的具体构造以及土体物理力学参数略。

按照文献[7]的方法进行码头建模，即采用非线性Winkler地基上的梁模型考虑桩-土相互作用，土体采用土弹簧模拟，土弹簧的荷载变形曲线由土的p-y(反力-位移)曲线确定，桩非线性由塑性铰模拟；另外，考虑上部结构刚度较大，将其设为刚性，建模在商业软件SAP2000中完成，然后按照3.1节的流程开展分析，得到各案例的计算结果。对模型进行非线性时程分析考虑两种弹性阻尼比，即0.05和0.10，以与前文阻尼比公式采用的弹性阻尼比值对应，除式(1)外的公式均采用0.05的弹性阻尼比。

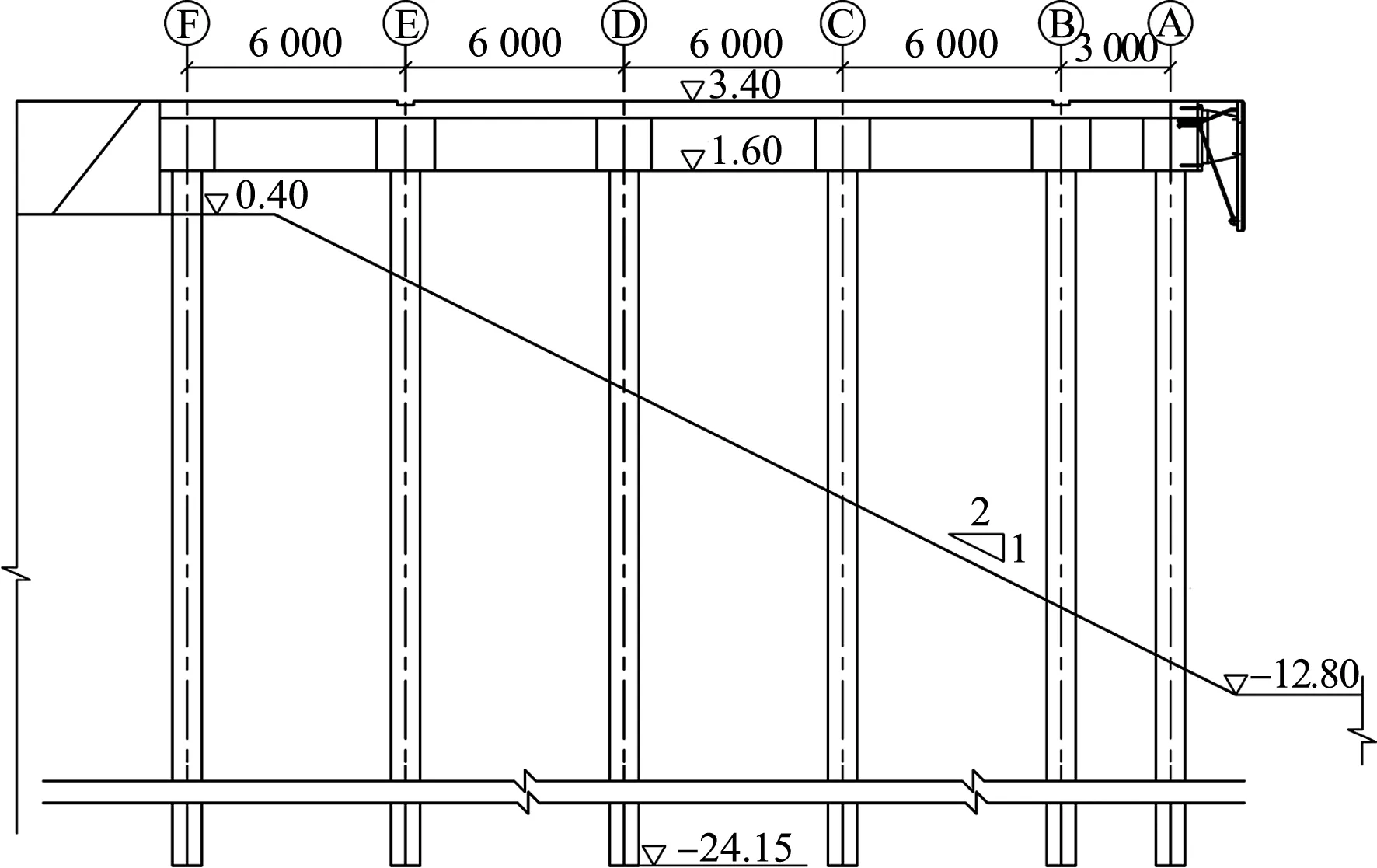
图5 码头横断面(尺寸：mm；高程：m)

4 结果与讨论

4.1 案例1

案例1的码头Pushover曲线见图6a)，图中标示出首个桩塑性铰形成时的位置。根据前述阻尼比计算公式确定的阻尼比随位移的变化趋势见图6b)，为便于不同公式进行对比，未将位移转化成延性系数。可以看出，不同公式的阻尼比值差别较大，其中式(4)的阻尼比值最大，但与式(3)相差不大；式(1)(2)在位移较小时差别较大，位移较大时差别不大，由于式(1)(2)均未能考虑土体耗能，故阻尼值偏小。

图6 案例1的Pushover曲线和等效阻尼比

替代结构法和非线性时程分析法确定的位移需求见图7，图中给出位移结果的相关系数ρΔ。可以看出，替代结构法的位移需求与时程分析结果相关性很强，相关系数均接近于1，说明采用替代结构法近似计算最大弹塑性位移反应是合理的。总体而言，式(3)(4)的相关性较高，式(2)的相关性最差。

图7 案例1位移需求分析结果

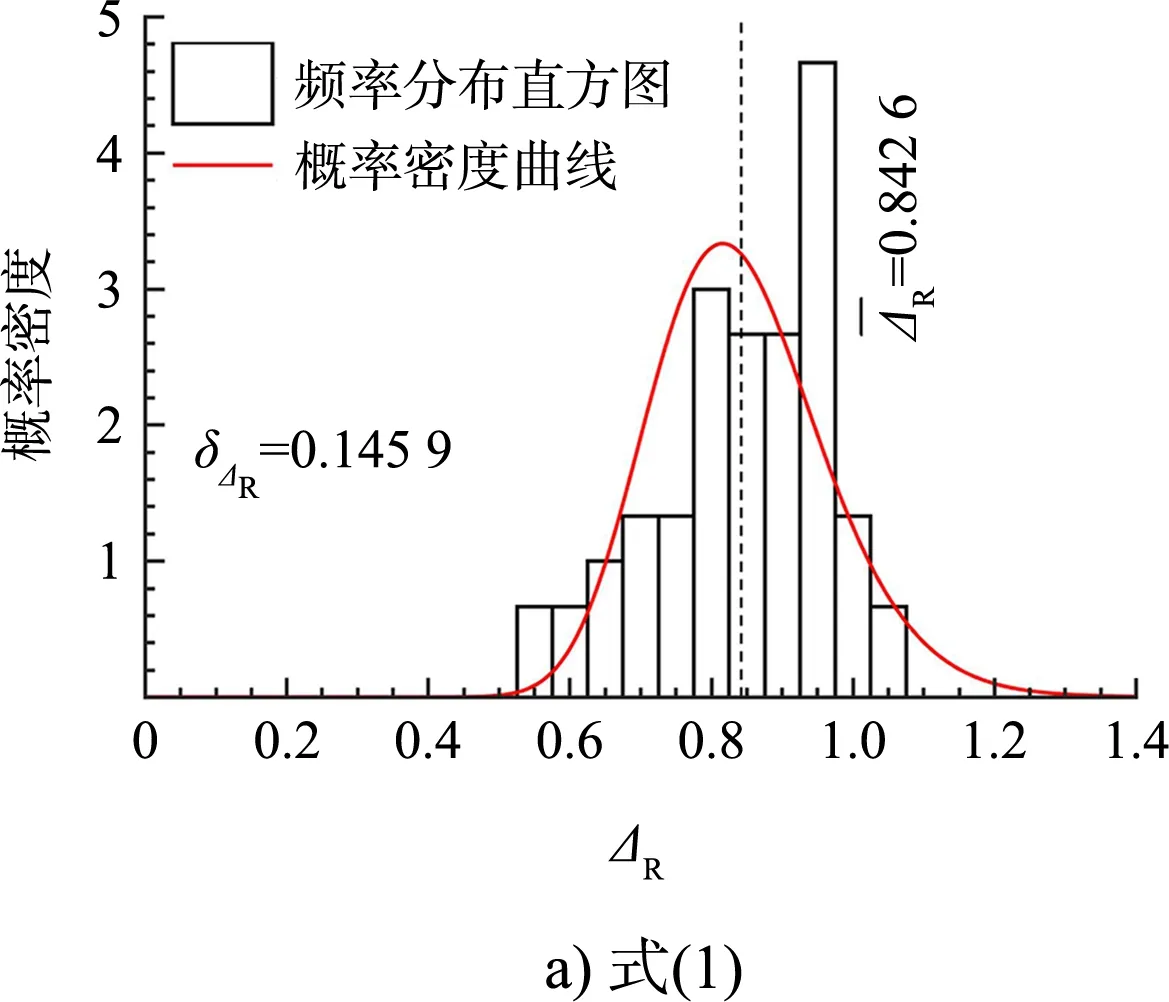
图8 案例1位移比频率分布和概率密度曲线

4.2 案例2

案例2 的Pushover曲线和等效阻尼比见图9。可以看出，与案例1的情况相似，式(3)(4)确定的阻尼比相差不大；与案例1不同的是式(1)(2)确定的阻尼比较大，这是因为案例2的桩基是预应力管桩，耗能能力弱于案例1的灌注桩，而式(1)(2)均是基于普通混凝土得到的，将其用于预应力结构会高估阻尼比。

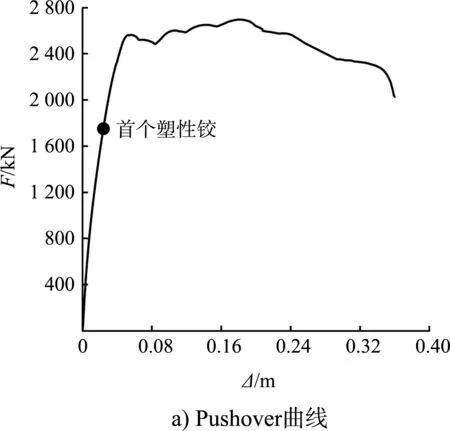
图9 案例2的Pushover曲线和等效阻尼比

两种位移需求分析方法的结果见图10。可以看出，式(3)(4)确定的位移与时程分析结果相关性较强，式(1)相关性最差；与案例1相比，两种方法分析结果的相关性变差，特别是式(1)(2)。

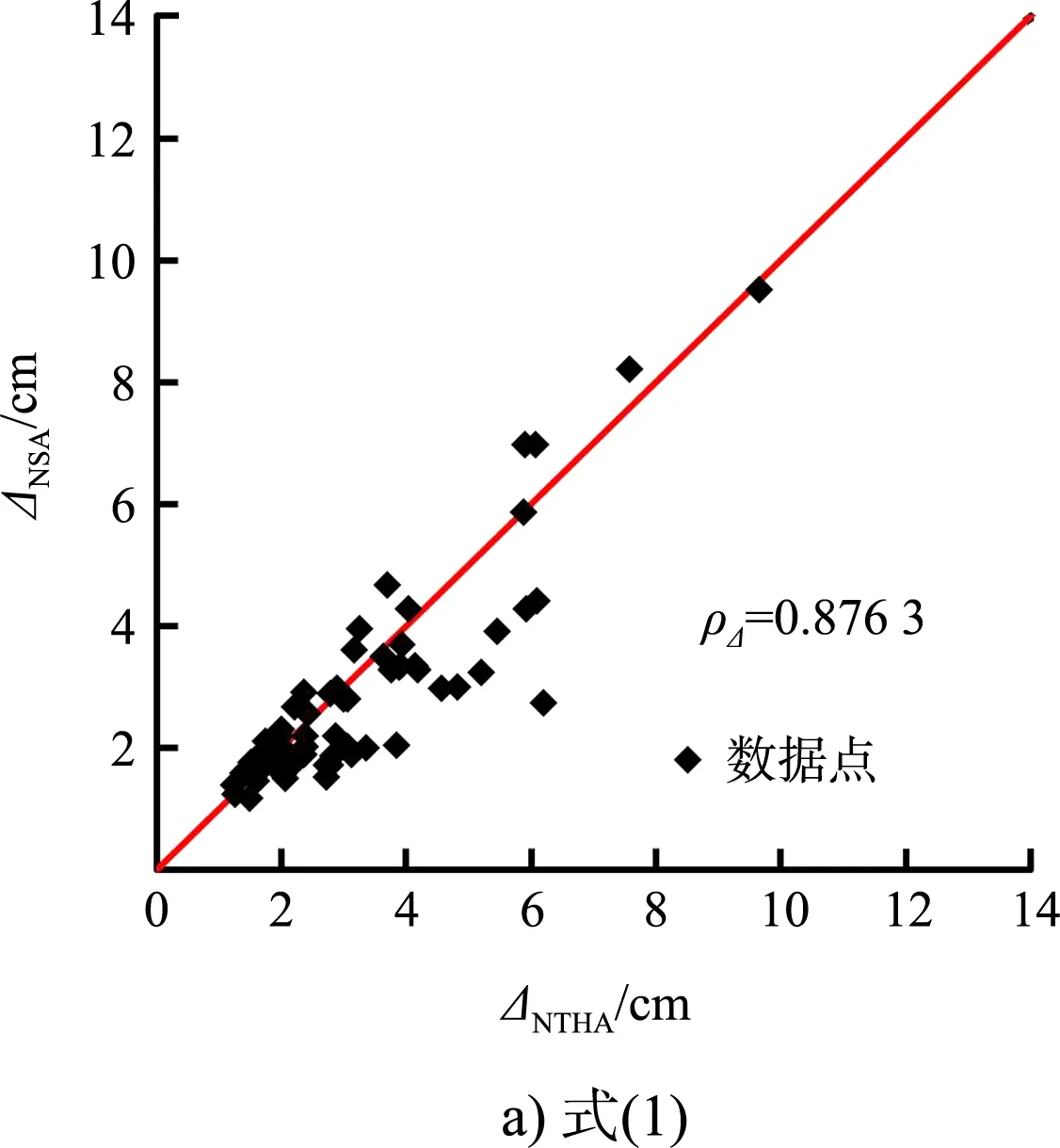
图10 案例2位移需求分析结果

位移比频率分布和相应的对数正态概率密度曲线见图11。K-S假设检验结果表明，位移比服从对数正态分布。由图11可看出，式(2)的位移比均值最小，式(3)(4)次之，但式(1)(2)的离散性较大；所有公式的位移比均大于1，说明对于预应力桩码头，替代结构法会低估位移需求。

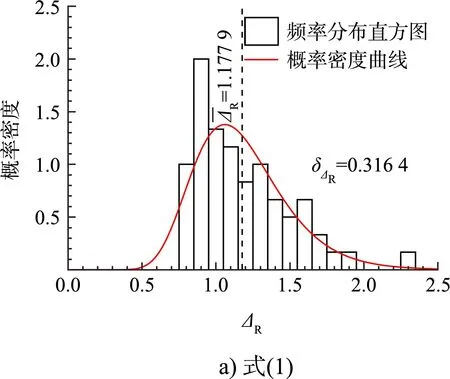
图11 案例2位移比频率分布和概率密度曲线

4.3 案例3

案例3的Pushover曲线和阻尼比见图12，与案例1、2的情况相似，由式(3)(8)确定的阻尼比相差不大；式(1)的阻尼比最小，说明采用基于普通混凝土构件的阻尼比公式会大幅低估钢管桩码头的阻尼比。

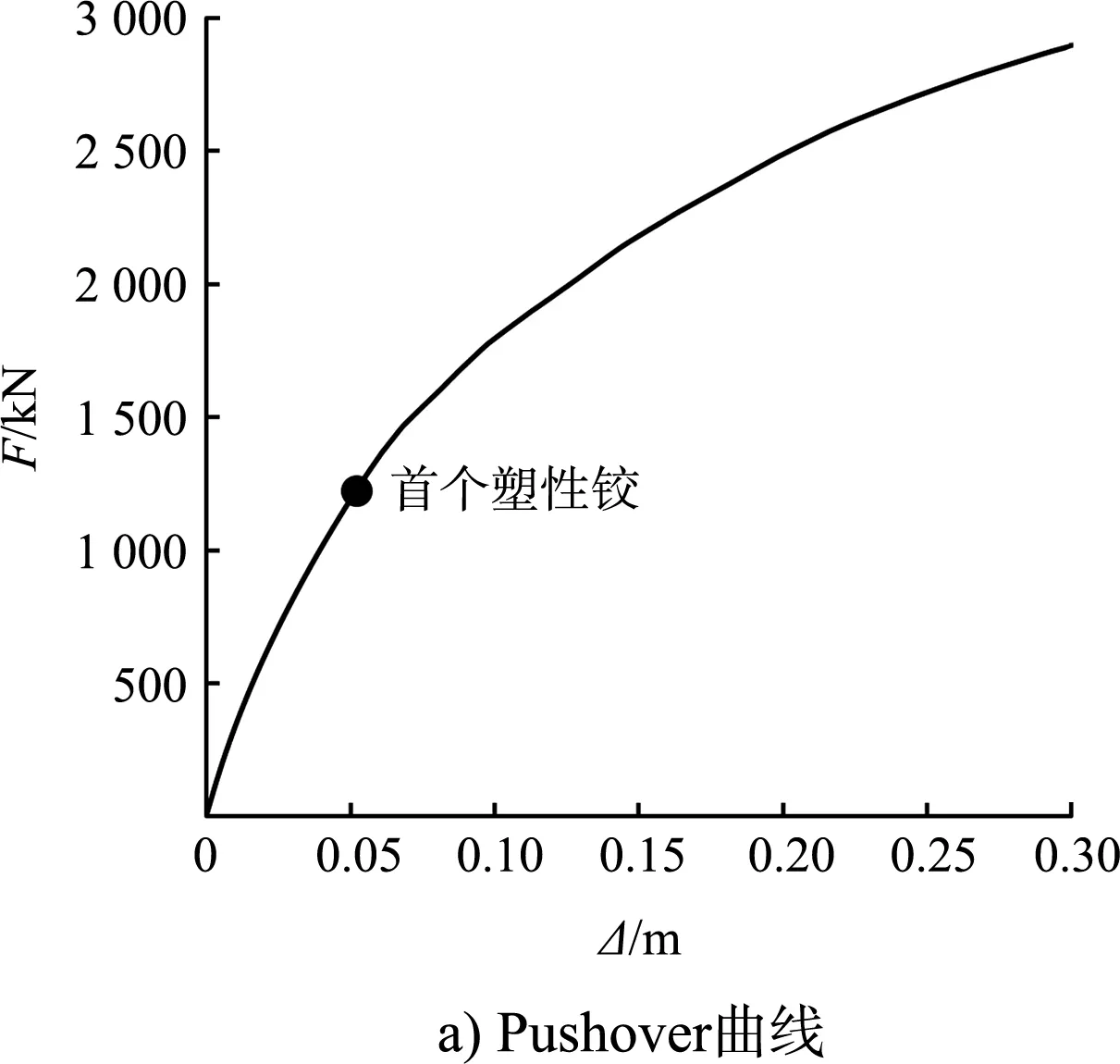
图12 案例3的Pushover曲线和等效阻尼比

案例3的位移需求计算结果见图13。可以看出，式(3)(8)的相关性更高，式(2)的相关性最差；与案例2相比，替代结构法的计算结果与时程分析结果的相关性变好，与案例1差不多。

图13 案例3位移需求分析结果

位移比的频率直方图和概率密度曲线见图14。K-S假设检验结果表明，位移比同样服从对数正态分布。由图14可看出式(2)的位移比均值最小，与1的偏差最大，精度最差，且离散性也最大；式(1)的位移比均值与1的偏差最小，精度最好，但离散性较大；式(3)与式(8)的精度差不多，位移比均值均大于1，说明两式的分析结果会低估位移需求，但式(8)的离散性最小。

图14 案例3位移比频率分布和概率密度曲线

4.4 讨论

(13)

(14)

(15)

式中：P(·)为概率函数；Φ(·)为标准正态分布函数。

对于式(2)，由式(13)计算可知，均值的保证率只有约56%，保证率偏低。那么对于常用的75%和95%的保证率，位移比ΔR，75%和ΔR，95%的计算公式为：

lnΔR，75%=μlnΔR+0.675σlnΔR

(16)

lnΔR，95%=μlnΔR+1.645σlnΔR

(17)

5 结论

1)相比于非线性时程分析方法，替代结构法是一种近似的位移需求简便分析方法，两种方法的计算结果相关性强，二者位移需求之比均值在0.8～1.2，但受等效阻尼比模型影响较大。

2)由长滩港码头设计标准和美国土木工程师协会规范ASCE/COPRI 61-14中阻尼比计算式确定的位移需求精度不如文献中的计算公式，且结果离散性较大，长滩港标准的计算公式对于灌注桩和钢管桩码头精度较高，ASCE/COPRI 61-14中计算公式对于预应力桩码头精度较佳，文献中的计算公式可作为设计参考使用。

3)对于灌注桩码头，替代结构法会高估位移需求，偏于安全；对于预应力桩码头，替代结构法会低估位移需求，对于ASCE/COPRI 61-14中阻尼比计算公式，当保证率分别取50%左右、75%和95%时，建议对其位移需求分别乘以1.10、1.25和1.65以提高结果的可靠性；对于钢管桩码头，规范中的计算公式会高估位移需求，但文献中的公式会低估位移需求，当保证率分别取50%左右、75%和95%时，可分别考虑1.10、1.20和1.35的放大系数。