波浪作用下矩形沉箱墩群受力规律试验研究*

张亚敬，刘海源，刘鸣洋，陈汉宝

(交通运输部天津水运工程科学研究所，港口水工建筑技术国家工程研究中心，工程泥沙交通行业重点实验室，天津300456)

随着港口工程大型化以及深水岸线资源的缺乏，离岸深水码头建设越来越多。重力式码头要求地基基础好，同时深水海域浪大、流急导致施工困难，结构断面庞大且造价高，因此墩柱式透空结构或桩基结构码头成为相对较好的结构形式。由于墩柱式透空结构码头的沉箱墩并不是孤立存在，波浪传播至墩群中时存在墩间反射、绕射，使得群墩之间的波高分布呈现出不同于单墩周围的波高分布规律，从而影响码头面高程设计以及沉箱墩受力计算。我国现行规范对透空式码头面高程的设计并未考虑群墩效应，定义群墩中波浪力衰减程度的群墩系数也仅适用于圆柱形墩，并不能反映矩形墩群中的波浪力变化规律。

关于群墩波浪力分布规律，已有许多研究者开展了相关研究。季新然[1]通过物理模型试验分析多向不规则波与群墩作用时波浪在大尺度圆形墩柱上的正向力、横向力和爬高，同时建立多向不规则波浪与大尺度墩柱及群墩结构作用的计算方法，给出不同布置形式的群墩系数，发现了不规则波作用下的波浪俘获现象；许佳[2]建立数值计算方法，对多向不规则波与大尺度群墩结构的作用进行模拟计算，分析不同布置形式群墩受横向力和正向力的变化规律；任效忠等[3]通过物理模型试验研究不规则波对准椭圆沉箱群墩结构的作用力，分析入射波向、周期、相对间距等因素与沉箱所受波浪力之间的关系，之后又进一步开展模型试验[4]研究规则波对准椭圆沉箱群墩结构的波浪力，发现与正向波浪力相比，群墩效应对横向波浪力的影响更大，对于大型结构准椭圆沉箱，波浪非线性的影响不容忽视；王永学[5]提出求解任意截面群墩结构波浪荷载的数值计算方法，对2个方形等截面群墩的系数进行研究，探讨群墩截面几何形状不同与群墩间相互影响的关系；周枝荣等[6]通过物理模型试验，研究矩形重力墩及墩间面板在斜向波浪作用下的波浪力大小及其群墩折减情况，提出矩形重力墩结构上最大总水平波浪力简化计算公式。可以看出，已有研究绝大多数揭示的是圆柱形群墩受力规律，针对矩形群墩的受力规律研究则远不及对圆柱形墩的研究丰富。因此，需要开展模型试验研究，观察和揭示矩形群墩式码头的墩间波高分布规律以及波浪力在墩间的衰减规律。

本文以茂名某墩式散货码头工程为例，通过开展三维物理模型试验，研究波浪作用下矩形沉箱墩群周围的波高分布及沿程衰减规律，研究代表性沉箱墩所受水平、侧向和浮托总力以及倾覆力矩，研究波浪力沿码头轴线方向的衰减规律。

1 工程概况

本工程位于茂名港博贺新港区大宗干散货作业区中突堤东侧岸线，中突堤西侧岸线为已建的粤电项目配套码头工程。从南向北连续建设1个20万吨级(M7)、1个10万吨级(M8)和1个5万吨级散货泊位(M9)，水工结构分别按照30万、20万和10万吨级预留。拟建工程码头结构总长度960 m，其中20万吨级泊位长度447 m，10万吨级泊位长度276 m，5万吨级泊位长度237 m，栈桥结构长度401.7 m，均采用透空式墩台结构，墩台之间采用大跨度预应力梁连接。距离码头前沿线102.4 m处为已建的粤电防波堤。工程位置如图1所示，工程区域平面布置见图2。

图1 工程位置

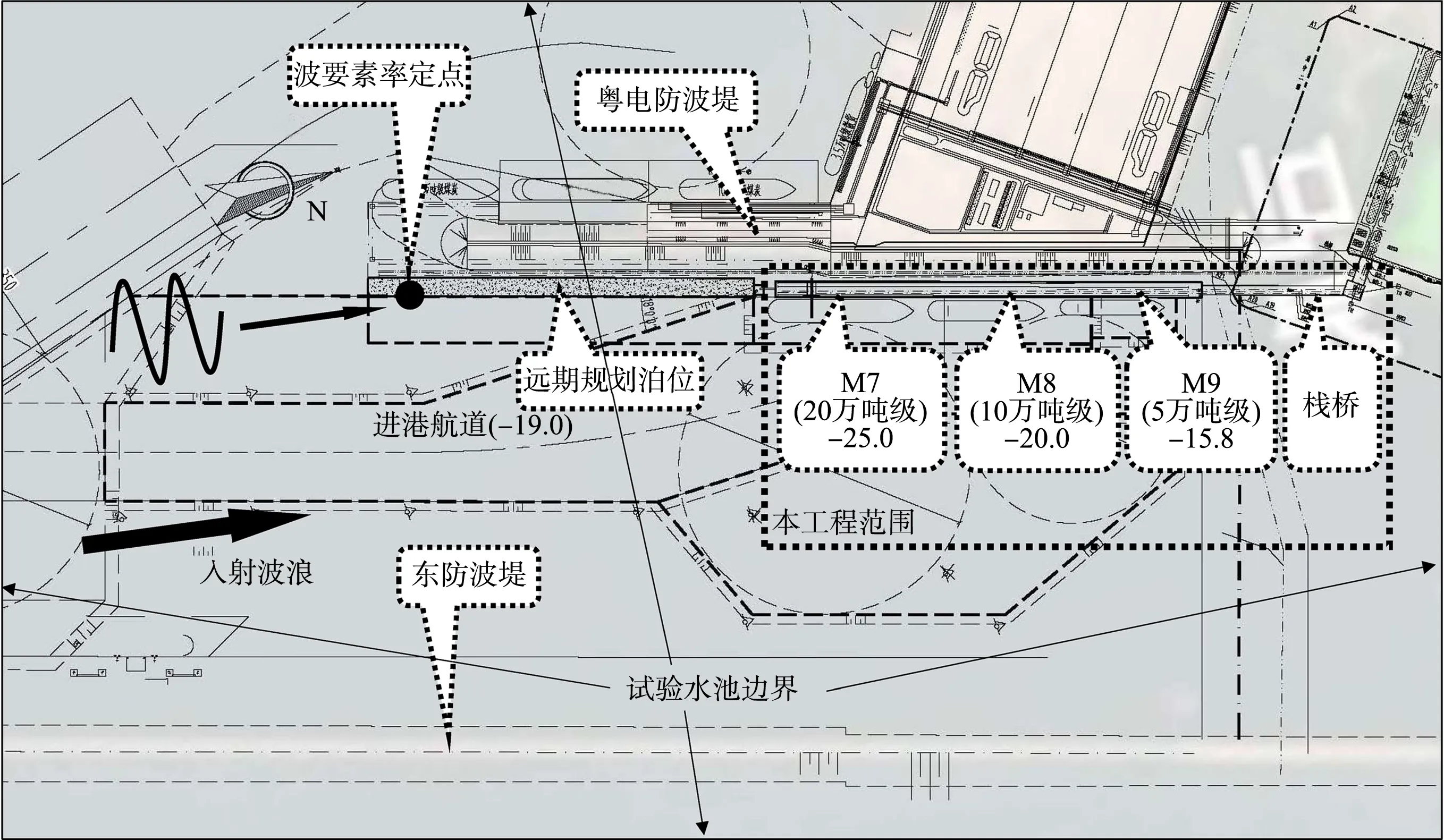
图2 工程平面布置(单位：m)

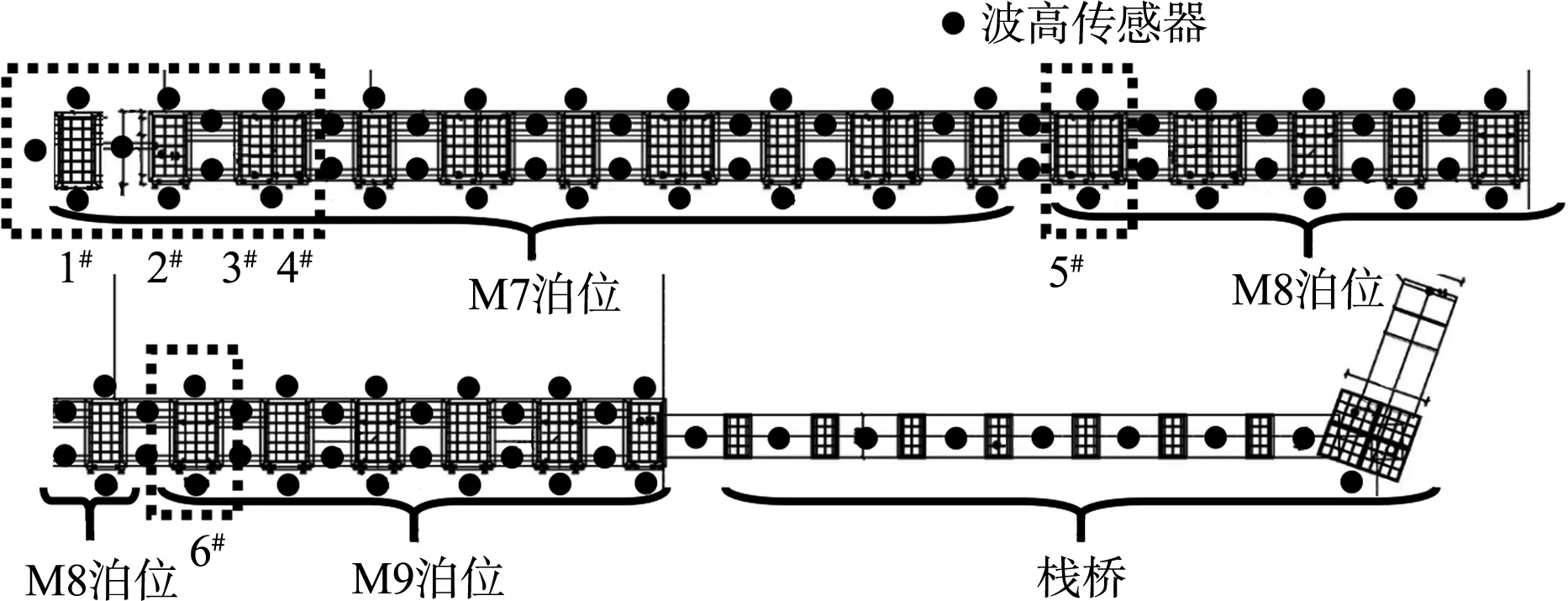
图3 沉箱墩布置及波高传感器分布

图4 代表性沉箱墩(M7泊位)结构断面(单位：m)

表1 率定点波要素

2 试验方法与试验工况

2.1 模型制作

模型试验在交通运输部天津水运工程科学研究院综合试验厅中完成。模型按重力相似准则设计，采用正态、定床模型。试验场地为55 m×42.5 m×1 m(长×宽×高)的矩形水池(试验水池边界见图2)，采用几何比尺λL为55。模型中粤电防波堤、东西防波堤和本工程沉箱墩的护底以及沉箱墩与粤电防波堤之间的护坡结构中的各种块石按重力比尺挑选，粒径级配符合《防波堤与护岸设计规范》[8]以及《波浪模型试验规程》[9]的要求。本工程港池内的水底地形包括航道、码头前沿以及天然地形，按照试验规程采用水准仪进行高程控制，偏差控制在±1 mm以内；工程区域所有结构的平面尺寸及位置偏差控制在±1 cm以内。矩形沉箱墩、预应力箱梁和码头面板等根据设计图纸采用木板组装制作，并根据试验规程和设计水位在沉箱墩的侧立面和底板预留安装压强传感器的孔位。

2.2 试验设备及方法

造波采用可移动摇板式造波机及其控制系统。模型造波时，由计算机根据输入的造波参数计算出目标波浪的板前波浪信号，并按一定算法将其转换成相当于造波板运动速度和位置的数据，由伺服驱动器输出脉冲信号控制伺服电机的转速和转动的角度，从而造出期望的波浪。本模型试验研究采用不规则波进行，不规则波根据《港口与航道水文规范》[10]采用JONSWAP谱进行频谱模拟，其解析式为：

Sη(f)=

(1)

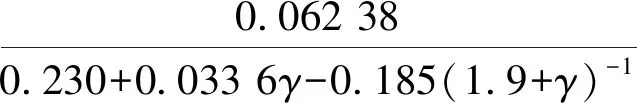
(1.094-0.019 15lnγ)

(2)

Tp=Ts/[1-0.132(γ+0.2)-0.559]或

(3)

(4)

本试验水位采用表1的设计水位。根据试验要求，各个试验水位依据给定的波浪要素进行率定，率定误差控制在0%～5%范围内，产生严格控制的正向偏差以保证实际造波波要素偏差的一致性。每组波要素的波列都保持波个数在100以上，将最后得到的造波参数存储在计算机中。正式试验前，均应用小波持续作用一段时间。模型试验采用TK-2008型动态水位测量系统(仪器精度为1.0 mm)对波高进行采集分析。波高传感器布置在每个沉箱的前沿、后沿以及之间(图3)，以记录波浪在沉箱之间的分布情况和沿程衰减规律。

各个矩形沉箱墩所受前后向、侧向和浮托总力采用两种测力方式取得，其一为利用2010型总力仪直接测量总力；其二为利用布置在沉箱侧立面和底板的若干压强传感器，测得压强值与其代表面积进行积分得到各个方向的总力。总力仪测力原理为：在两个平整的刚性矩形面板之间的4个角上分别布置4个三维测力天平，其中一个矩形面板与所测结构刚性固接，另一个矩形面板与刚性足够大的固定支架固接，所测结构形心在平面上的投影与传感器矩形面板的形心重合；结构所受的力传递到与其固接的总力仪时，每个测力天平可测得其所受的3个分力Fxn、Fyn和Fzn；根据六分力原理，由所有测力天平上的共计12个分力可计算得出结构整体所受的6个分力，即水平总力Fx、侧向总力Fy、浮托总力Fz、x轴力矩Mx、y轴力矩My和z轴力矩Mz。各个力的关系见式(5)，力的分布见图5。

图5 总力仪原理

(5)

式中：Lx和Ly分别为每个力传感器之间在x和y方向上的距离。

对于由压强值积分得到总力的方式，依据《波浪模型试验规程》和试验技术要求，在沉箱结构的底面和侧面布置相应数量的压强传感器，其中沉箱上部静水面附近布置的传感器密度比下部大，综合考虑不同设计水位，并保证能够准确捕捉到波峰波谷变化导致的沉箱壁面所受波压强的变化。波压力数据通过SG2008型数据采集系统进行采集分析，试验中连续采集至少100个波作用的波压力过程，模型采样的时间间隔均为0.01 s。试验时在静水条件下，对所有测点标零，在静水面以下的测点以此时的静水压强作为对应测点的零点，在静水面以上的测点以此时的大气压强作为零点。试验采集到的压强值为测点实际压强与标零时测点对应压强的差值。将沉箱置于x、y、z坐标轴所构成的三维直角坐标系内，然后将各测点所代表的压强和面积在该坐标系x、y、z3个方向分别进行投影，再由各测点测得压强过程线，利用积分得到在x、y、z3个方向所受到的波浪力，最后统计其所受总的水平力Fx、侧向力Fy和浮托力Fz。对于力的方向规定为：Fx与x轴正方向相同为正，反之为负，Fy和Fz的规定与Fx相同。将沉箱沿前后和两侧方向的倾覆力矩的旋转中心定义为沉箱底板两个方向的中心线，则结合每个测点受力所对应的力臂，可以得到沉箱在前后以及两侧的总倾覆力矩，即My和Mx。压强传感器的布置方式如图6所示，图中箭头所指方向分别定义了x、y、z3个方向的总力以及沿前后和两侧倾覆力矩的正方向。同时，将总力仪得到的力和力矩与图6所示坐标系相统一。

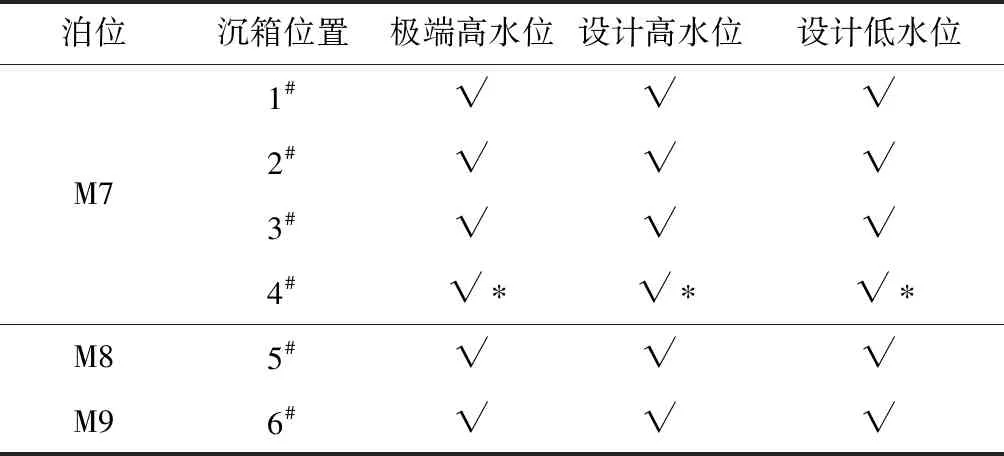
表2 试验工况

图6 压强传感器布置方式以及本文定义坐标系

2.3 试验工况

本文针对该工程实例的不同泊位的沉箱间波高分布以及代表性沉箱墩所受的波浪力变化规律进行研究。观察在极端高水位、设计高水位和设计低水位，重现期为50和10 a的波浪条件下，沉箱间波浪传播现象和波高沿程衰减规律，揭示各泊位代表性矩形沉箱墩所受波浪力的沿程变化规律。对于沉箱间波高分布，本模型试验的沉箱墩上均不放置预应力箱梁，以排除预应力箱梁与水体接触对沉箱间波高产生的干扰。对于波浪力，沿码头轴线方向选取M7泊位的系缆墩沉箱、第1个单沉箱、第1个双沉箱南侧沉箱和第1个双沉箱北侧沉箱，选取M8泊位第1个双沉箱南侧沉箱，选取M9泊位第1个单沉箱，以进行墩群中波浪力沿程变化规律的研究。将上述代表性沉箱按顺序进行编号1#～6#，其位置如图3中虚线框和标记所示，试验工况和组次见表2。

3 试验结果与分析

3.1 沉箱间波高分布

试验中对港区的波浪传播情况进行观察，发现港池和航道存在挖深的情况下，加上粤电防波堤的影响，波浪经过率定点后传至本工程区域时，其传播方向基本与码头轴线方向一致。通过波高传感器所采集的数据发现，不同水位不同重现期波浪条件下，该码头沉箱墩区域波高沿程分布呈现出相似的规律，即：受沉箱侧面的阻水和反射的影响，沿码头轴线方向，位于M7泊位南端5个沉箱墩范围内波高衰减幅度最大。以最不利的极端高水位重现期50 a的波浪作用为例，M7泊位1#墩南侧测点H1%=7.38 m，随后沿码头轴线方向逐渐衰减，至M7泊位第6个沉箱时H1%=3.07 m，波高衰减58.4%；至M8泊位的5#墩时H1%=1.87 m，波高衰减74.7%；至M9泊位所有沉箱H1%均在1.40 m左右，波高衰减81.0%。极端高水位重现期50 a波浪条件下代表性沉箱四周H1%分布沿程变化如图7所示，其中图7b)为归一化的波高值，其定义为该沉箱的前沿、后沿、沉箱间前侧或沉箱间后侧位置的波高与M7泊位1#墩四周相应位置波高的比值。对波高沿程衰减幅度最大的M7泊位南端5个沉箱区域的波高分布进行观察可知：受相邻沉箱侧壁的入射波与反射波叠加的影响，波高分布呈现两沉箱间波高>沉箱前沿波高>沉箱后沿波高的规律；而随着波高由南向北沿程衰减，其余位置各沉箱四周波高差别也逐渐减小。

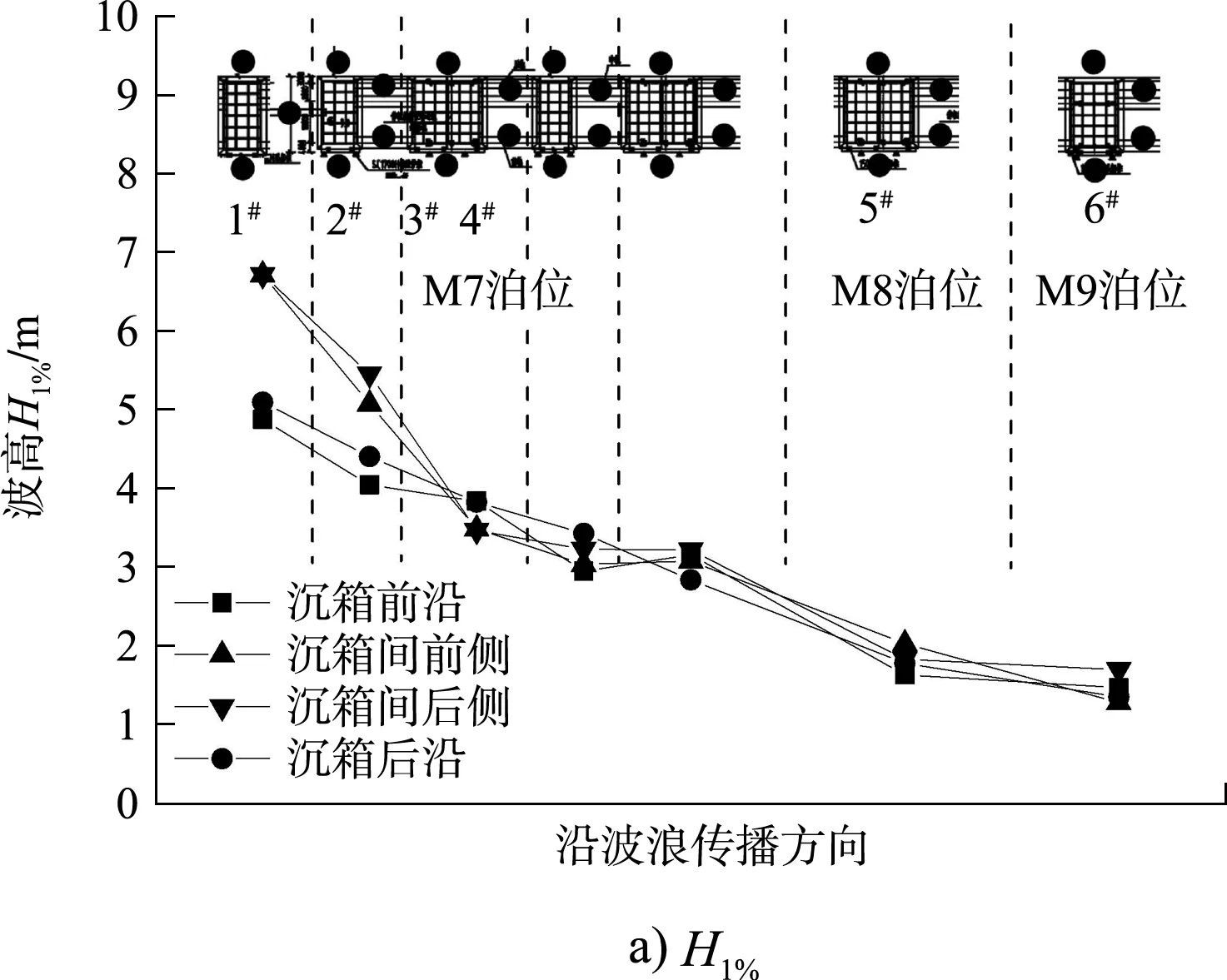
图7 极端高水位重现期50 a波浪条件下代表性沉箱H1%波高沿程变化

3.2 沉箱受力

根据表2所列试验工况，对选取的不同泊位的沉箱进行受力测量，结果见表3、4。其中表3为首先受到波浪作用的M7泊位系缆墩(1#墩)的受力结果，可以看出，由总力仪直接测量得到的沉箱在各个方向所受波浪力和力矩，与由压强传感器所测压强值积分所得结果较为接近，且呈现出的随设计水位和波浪重现期的变化规律是一致的，即沉箱所受的水平力Fx、侧向力Fy、浮托力Fz以及侧向倾覆力矩Mx和前后倾覆力矩My均与设计水位和波高呈正相关。以上结果也验证了本文采用的模型试验方法以及试验过程。

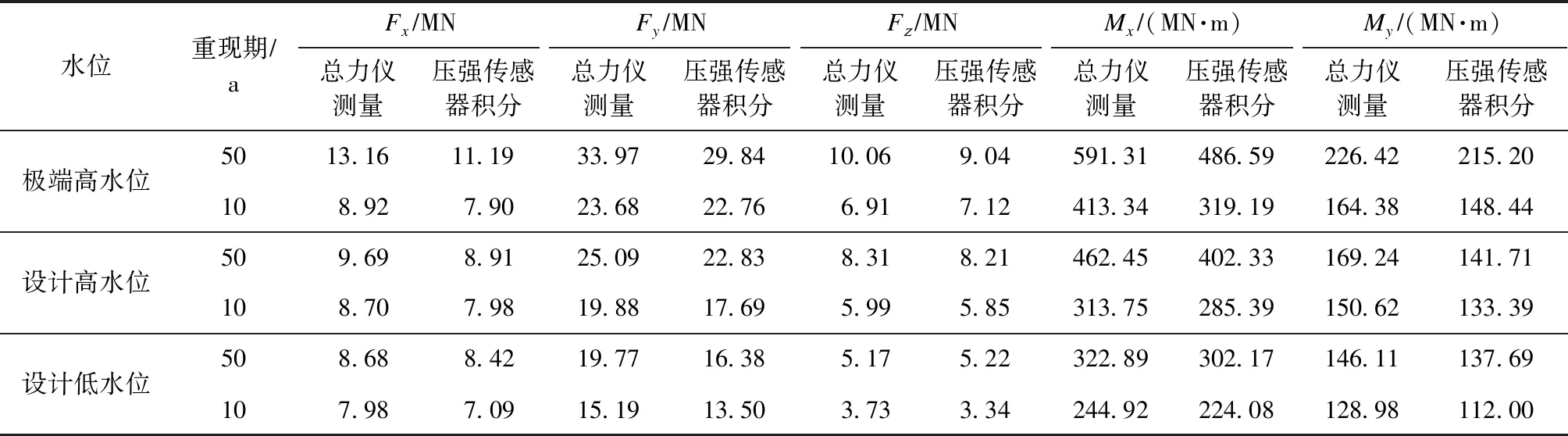
表3 M7泊位1#墩受力结果

表4为所有选取的代表性沉箱(1#～6#墩)在极端高水位和重现期50 a的波浪条件下，所受波浪力的对比。极端高水位重现期50 a波浪条件下代表性沉箱受力沿程变化如图8所示，其中纵坐标为归一化的各沉箱受力值，其定义为该沉箱在某个方向的总力(Fx、Fy或Fz)或倾覆力矩(Mx或My)与M7泊位1#墩所受相应的力或力矩的比值。可以看出，不同沉箱所受波浪力的沿程衰减幅度，呈现出与沉箱周围波高沿程衰减情况一致的规律，即：作用在M7泊位3#和4#墩的波浪力相比M7泊位1#墩所受波浪力已经发生了很大程度的衰减；从M7泊位3#和4#墩开始沿码头轴线方向向北，直到M8和M9泊位，沉箱所受波浪力不再有明显衰减。

表4 极端高水位下重现期50 a波浪的不同泊位代表性沉箱墩受力结果

图8 极端高水位重现期50 a波浪条件下代表性沉箱受力沿程变化

3.3 波浪力衰减规律

本文的矩形沉箱墩形成了串列式的墩群，波浪在矩形沉箱墩组成的墩群中的衰减导致的沉箱所受波浪力的衰减规律，尚未有试验进行研究。本文针对M7泊位1#～3#墩的串列结构进行群墩系数计算。由于波浪入射方向与码头轴线走向非常接近，故本文研究y方向的波浪侧向总力Fy的变化规律。根据《港口与航道水文规范》中群墩系数的定义和计算方法，对以上选取的3个沉箱墩结构所受y方向的波浪总力Fy的沿程衰减情况进行计算，并与模型试验所得结果进行对比。《港口与航道水文规范》定义的参数k(由谱峰周期Tp对应的波长Lp定义的波数，k=2π/Lp，得0.03)和D(圆柱体直径，本文定义为矩形沉箱上垂直于码头轴线方向的尺度，即矩形沉箱沿码头前后方向的长度，取27.55 m)，对于本文矩形沉箱的kD=0.83。则根据规范计算所得群墩系数为：M7泊位2#墩(距离1#墩45 m)，群墩系数为0.99；M7泊位3#墩(距离1#墩90 m)，群墩系数为0.96。然而，本文模型试验得到的对应沉箱在y方向所受侧向力Fy的归一化结果分别为0.75和0.49，与规范计算所得结果相差较大。这是因为矩形沉箱墩存在较大面积的直立壁面，一方面阻水面积较大，另一方面波浪在沉箱间多次反射，致使波能衰减的幅度相比在圆柱形墩群中明显更大。因此，针对矩形沉箱组成结构的群墩系数计算，《港口与航道水文规范》的圆柱形墩的群墩系数计算方法不再适用。在后续工作中应开展系统性的试验研究，以得到适用于矩形沉箱的群墩系数计算方法。

4 结论

1)受沉箱侧面的阻水和反射的影响，沿码头轴线方向，位于M7泊位南端5个沉箱墩范围内波高衰减幅度最大；受相邻沉箱侧壁的入射波与反射波叠加的影响，波高分布呈现两沉箱间波高>沉箱前沿波高>沉箱后沿波高的规律，随着波高由南向北沿程衰减，其余位置各沉箱四周波高差别逐渐减小。

2)不同沉箱所受波浪力的沿程衰减幅度，呈现出与沉箱周围波高沿程衰减情况一致的规律。作用在M7泊位3#和4#墩的波浪力相比M7泊位1#墩所受波浪力已经发生了很大程度的衰减；从M7泊位3#和4#墩开始沿码头轴线方向向北，直到M8和M9泊位，沉箱所受波浪力不再有明显衰减。

3)矩形沉箱墩阻水面积较大，且波浪在沉箱间多次反射，致使波能衰减的幅度相比在圆柱形墩群中明显更大。针对矩形沉箱组成结构的群墩系数计算，规范中的圆柱形墩的群墩系数计算方法不再适用。