PC简支梁预应力效应与结构自振频率研究
周国贤
(北京市建设工程质量第三检测所有限责任公司,北京 100037)
0 引 言
随着预应力混凝土结构在我国桥梁工程领域的广泛应用,其在服役过程中受荷载和环境的影响,产生不同程度的预应力损失,导致结构的使用性能下降。准确快速识别现存有效预应力,对结构性能的量化评估具有重要意义。
利用结构自振频率来识别预应力筋的有效应力是一种理论可行的无损检测方法。由经典理论[1]提出的梁在轴向力作用下横向自由振动方程得到随轴向力增加,固有频率减小的结论,为预应力有效应力识别提供了理论依据。但Saiidi[2]等人对一系列预应力损失的情况进行动力试验表明一阶自振频率随着轴向力的增大而增大,与预测结果不符。对于Saiidi的试验结果:Dallasta和Dezi[3]认为在线弹性范围内,预应力对梁弯曲振动频率的影响可以忽略,出现上述情况是由于未考虑预应力筋的非线性效应。Jain和Goel则指出预应力属于结构内力,不会引起“压缩软化”效应。Miyamoto[4]等人分析体外预应力加固梁结构时建立的考虑预应力增量的运动方程却得到随预应力增大,自振频率趋于降低的结论。Chan和Yung[5]也在预应力识别的理论研究中指出“压缩软化”效应造成桥梁自振频率随预应力的增大而降低。而Hamed和Frostig[6]通过能量法对粘结与无粘结情况分析中得出预应力大小不会影响结构自振频率的结论。
同时,预应力效应与结构自振频率的关系受到多种因素的影响。张耀庭[7-8]等人通过对粘结和无粘结简支梁试验,都得到预应力增大,结构自振频率增大的结果。刘龄嘉[9]等人通过不同梁截面试验得出预应力对混凝土梁的振动频率的影响与梁截面形式有关,而且振动频率随预应力值的增大而增大。陈一飞[10]等人通过三根无粘结简支梁试验得出预应力对频率的影响分为前后两个阶段。(1)前期,自振频率随着预应力增加而增加;(2)后期,自振频率随着预应力增加而下降。并将其归结于预应力对混凝土内部微裂纹的作用。熊辉霞[11]等人基于损伤理论对结构弹性模量分析提出了负损伤理论,认为预应力提高了弹性模量,从而增强结构刚度。吴泽玉[12]等人又讨论了不同布筋形式对自振频率的影响,得到直线布筋对频率的影响小于折线布筋和曲线布筋,折线布筋对频率的影响略大于曲线布筋。谭国金[13]等人提出了偏心直线配筋的预应力简支梁自振频率计算方法,公式表明自振频率随预应力增大而增大,而且与偏心距有关。
目前,预应力效应机理尚未明确,现有的结构动力检测方法并不能直接用于评估桥梁的内力状态,尤其是预应力桥梁结构中现存应力的识别。预应力构件作为结构的承重体系的主要构件,预应力损失过大必定影响结构的安全性,而预应力效应机理及其影响因素研究是建立有效预应力快速识别指标的基础。
1 预应力效应机理分析
1.1 有无“压缩效应”分析
经典理论对承受轴向力的梁做出了分析,给出了考虑轴向力影响的梁的弯曲振动方程。
(1)
自振频率表达式为
(2)
式中:m(x)为分布质量;N为轴力;EI(x)为弯曲刚度;ωn为n阶自振频率。
显然,轴向力与曲率的乘积形成了作用在梁上的附加竖向荷载,导致频率降低。
值得注意的是,经典模型中的轴向力与预应力产生的等效轴力并不相同,对于预应力结构,任何配筋形式的梁在振动过程中,预应力筋与梁轴线相对位置不会发生改变,其产生的等效轴力方向会随曲率变化而变化,从而振动方程中轴力与曲率的乘积始终为零,微元两侧轴力受到预应力筋长度变化的影响,数值会增大,但不会对梁产生附加竖向荷载,即预应力等效轴力只是改变了结构的应力水平,并不会引起“压缩软化”效应,其横向振动方程仍为
=P(x,t)
(3)
自振频率计算式为
(4)
1.2 影响因素分析
公式(4)表明结构自振频率与跨度L、弹性模量E、截面惯性矩I、分布质量m有关。结构跨度是结构设计的重要参数之一,高跨比能够直接反应结构的整体刚度,从而对结构自振频率产生直接影响。然而,对于已有预应力结构,跨度和质量往往是固定的,不会引起自振频率的变化。文献[11]中试验表明应力水平与材料弹性模量之间存在关系。预应力结构中由于预应力的存在,给予了结构一个初始的应力状态,从而引起材料内部的变化,使得混凝土原生微裂缝收缩,从而提高弹性模量,增强结构刚度,结构自振频率随预应力的增大而增大。随预应力的不断增大,结构处于高应力状态,当预应力达到一定限值时,继续增大预应力,混凝土内部开始出现由预应力产生的次生微裂缝,降低了结构的刚度,导致自振频率下降,从而表现出两阶段的性质。结构采用不同的配筋形式和偏心距会影响截面惯性矩的计算,对于曲线和折线配筋的桥梁结构,截面惯性矩沿桥梁长度方向发生变化,由于配筋形式引起截面惯性矩变化导致结构的自振频率与配筋形式有关。对于直线配筋的结构,截面惯性矩沿梁的长度不会发生变化,但是改变偏心距同样会对截面惯性矩产生影响。因此,预应力效应对结构自振频率的影响是预应力对弹性模量和截面惯性矩综合作用的结果。
2 粘结和无粘结机理分析
2.1 截面惯性矩取值
对于粘结和无粘结预应力结构均不会产生“压缩软化”效应,二者在预应力大小等值的情况下使结构处于相同的应力状态,所以弹性模量变化是相同的。但是对于粘结预应力结构,预应力筋与混凝土之间能够共同工作,设计[14]中采用换算截面计算结构刚度,而无粘结预应力结构预应力筋与混凝土之间可以相对滑动,采用去除管道面积的净截面计算结构刚度。考虑截面惯性矩取值,粘结预应力结构的自振频率要大于无粘结预应力结构。
2.2 变形协调
在振动过程中,由于混凝土与预应力筋之间存在粘结力,使得预应力筋的变形与周围混凝土的变形保持一致,即在动力反应中,预应力筋与混凝土变形协调。对于无粘结预应力结构预应力筋与混凝土之间可以发生相对滑动,预应力筋的变形与周围混凝土的(轴向)变形并不一致。为了分析粘结与无粘结预应力结构变形协调对自振频率的影响,可以将预应力结构视为混凝土与预应力筋两个子结构,计算预应力筋对整体结构刚度的贡献大小。忽略预应力筋的弯曲刚度(拉力影响的分布参数体系),其自振频率可采用下式[6]。
(5)
式中:Lcable、mcable和T分别表示预应力筋长度、分布质量和拉力。
可以看到,影响预应力筋自振频率的关键参数是拉力T。在拉力相同的情况下,预应力筋对结构刚度贡献与其和混凝土工作时的接触方式有关。粘结预应力筋受到周围混凝土的固结约束,而由于无粘结预应力筋存在套管,混凝土不能形成对预应力筋的轴向约束,使得在振动过程中,无粘结预应力筋的轴向应变小于相应位置上混凝土的应变,粘结预应力筋则与相应位置混凝土应变相同。振动过程中,由于粘结预应力筋增量产生的附加拉力ΔT大于无粘结预应力筋产生的附加拉力ΔT′,从附加预应力大小的角度,粘结预应力结构自振频率大于无粘结预应力结构。
变形协调对自振频率的影响还可以从能量角度得到解答,体系中的总能量包括系统动能和应变能。
(6)
式中:E为系统总能量,EK为系统动能,ES为应变能,ρ为密度,u(x,t)为结构的横向位移,“·”表示位移对时间的导数,σx和εx、σxcab和εxcab分别表示混凝土应力应变和预应力筋应力应变。
由于预应力筋有无粘结与结构密度和结构横向位移无关,所以两种情况系统动能理论上等值,其主要差异在于系统应变能中由预应力筋变形产生的应变能。由上述对预应力筋附加拉力的分析可知,与混凝土接触方式导致无粘结预应力应变能小于粘结预应力筋应变能,即在给予结构相同初始振动条件下,采用无粘结形式的结构振动应变能总是小于相同条件下粘结预应力结构,即粘结预应力结构的刚度大于无粘结结构,粘结预应力结构自振频率大于无粘结预应力结构。
2.3 接触刚度
预应力筋有无粘结还存在与混凝土的接触刚度问题,对于接触刚度有如下结论[15]。动态相对位移幅值越大,动态接触刚度增量和接触阻尼也越大。粘结预应力筋与混凝土的接触刚度明显大于无粘结情况,所以在相同位移幅值情况下,其接触阻尼大于无粘结情况,已有试验[16]也表明粘结预应力结构阻尼较大,其耗能能力优于无粘结预应力结构。
粘结与无粘结预应力结构自振频率影响是上述三个方面的综合作用,对截面惯性矩取值和变形协调影响分析得到粘结预应力结构自振频率大于无粘结预应力结构,考虑接触阻尼,粘结预应力结构拥有较好的耗能能力。
3 分析验证
3.1 模型建立
对文献[16]中试验梁进行建模分析,梁的计算跨度为4 000 mm,矩形截面高300 mm,宽200 mm,截面上部配置2根直径14 mm的HRB335架立筋,底部配置3根直径18 mm的HRB335纵向钢筋,曲线配置2根预应力直径15.2 mm的低松弛高强钢绞线。梁体材料为C40混凝土,弹性模量为3.45×104MPa,阻尼比为0.05,预应力钢绞线弹性模量为1.95×105MPa,阻尼比为0.02。
模型采用一致质量法和Lanczos法对结构进行动力分析,得到结构的前三阶自振频率,模型所得数据与试验和ANSYS模型数据统计见表1。采用midas Civil建立的结构模型计算结果,一阶频率与试验数据的最大误差为3.7%。利用该模型可以分析不同线型的预应力筋自振频率的变化规律。
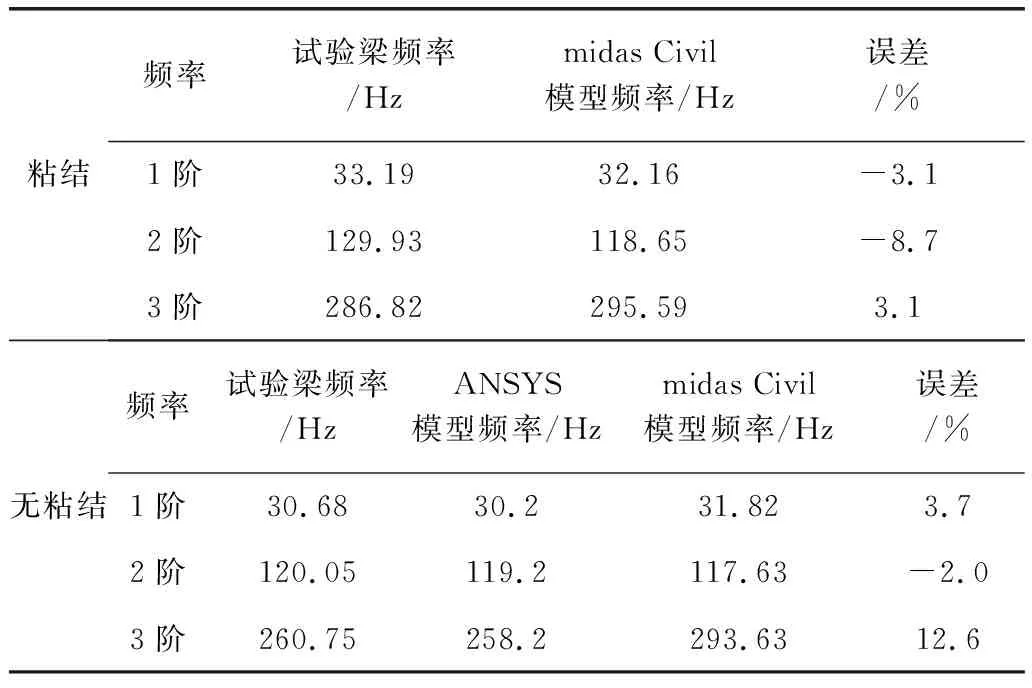
表1 模型结果与文献[16]数据对比
改变布筋形式和偏心距分析粘结与无粘结预应力结构,可以得到不同线型和不同偏心距简支梁的自振频率变化规律。对预应力筋形状分为直线、折线和抛物线三种,其中直线偏心距又分为0 mm、50 mm和100 mm三种,折线和抛物线偏心距分为50 mm和100 mm两种。运行分析得到不同条件下简支梁的一阶自振频率,通过比较不同条件下一阶频率的变化规律,分析偏心距和线型对粘结与无粘结预应力简支梁动力特性影响。
3.2 粘结预应力结果分析
对于粘结预应力结构,不同布筋形式的截面惯性矩的取值不同,相同偏心下,直线配筋沿梁长度方向上预应力筋换算面积与混凝土梁中性轴之间的距离不变,且数值与偏心距e相等。曲线配筋和折线配筋的预应力筋与中性轴之间的距离沿梁长度方向发生变化,且数值≤偏心距e。所以相同偏心距下,直线配筋惯性矩最大,曲线配筋略大于折线配筋,由自振频率计算式(4),结构自振频率:直线>曲线>折线。直线偏心不同偏心距,截面惯性矩按下式计算
I=Ih+Is+(αEp-1)Ap×e2
(7)
式中:Ih和Is分别表示混凝土截面惯性矩和普通钢筋的换算截面惯性矩,αEp为预应力筋弹性模量与混凝土弹性模量之比,AP为预应力钢筋截面面积,e为偏心距。
公式(7)表明截面惯性矩取值与偏心距e的平方成正比。结构自振频率随偏心距增大呈现非线性增长。
通过模型数据作图分析,发现对图粘结预应力不同条件下一阶频率的变化趋势与理论分析一致。
(1)相同偏心下,一阶频率直线布筋最大,曲线次之,折线最小,三者之间呈现线性增长关系。
(2)直线偏心下,一阶频率随偏心距增大呈现非线性增长,偏心距越大频率增长速率越快。
3.3 无粘结预应力结果分析
对于无粘结预应力结构,截面惯性矩采用去除孔道的净截面计算。
I=Ik+Is+[(αEp-1)Ap-AK]×e2
(8)
式中:AK为预应力孔道面积,其余各项含义同式(7)。由于直线配筋距离截面中性轴最远所以惯性矩损失最大,曲线次之,折线最小。由自振频率计算式,不同配筋形式的自振频率关系为:直线<曲线<折线。同理,直线配筋不同偏心的情况,自振频率随偏心距增长非线性下降。无粘结预应力不同条件下一阶频率的变化趋势与理论分析结果一致。
(1)相同偏心下,一阶频率折线布筋最大,曲线次之,直线最小,三者之间呈现线性增长关系。
(2)直线偏心下,一阶频率随偏心距增大呈现非线性下降,偏心距越大频率下降速率越快。
上述规律表明粘结预应力简支梁结构与无粘结预应力简支梁结构自振频率表现出相反的的性质。粘结预应力简支梁一阶自振频率按照直线布筋、曲线布筋和折线布筋依次近似线性递减(忽略考虑尺寸效应),而无粘结预应力简支梁则接近线性递增。考虑直线配筋不同偏心时,粘结预应力结构一阶自振频率随偏心距增加呈非线性增长,偏心距越大,频率越高,变化速率越快。无粘结一阶自振频率随偏心距增大快速降低,偏心距越大,频率越低。总体来看粘结预应力简支梁一阶频率要大于无粘结简支梁,其中直线布筋差别最为显著,曲线次之,折线最小,分别为1.24%、0.87%和0.47%。考虑截面惯性矩的影响,讨论预应力线型和偏心结构自振频率的变化时,粘结预应力和无粘结预应力的变化趋势相反,实际工作中应该将两者分开考虑。同时,表1中数据,无粘结和有粘结预应力筋的一阶频率试验结果分别为30.68 rad/s和33.19 rad/s,由频率计算公式(4),刚度比为频率比的平方,可以得到无粘结的刚度为有粘结的85.4%。
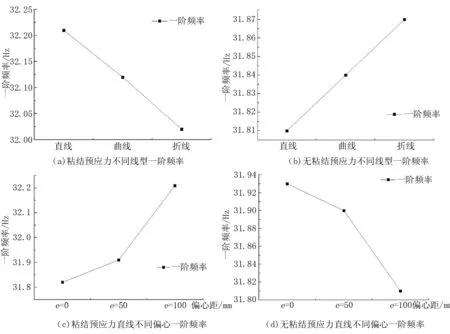
图1 粘结与无粘结预应力一阶频率变化趋势
4 结 论
(1)从有无竖向附加荷载分析预应力不会产生“压缩软化”效应,轴向力模型不适用于预应力结构。预应力效应通过引起弹性模量和截面惯性矩的变化影响结构自振频率。
(2)从截面惯性矩取值、变形协调和接触刚度讨论了粘结和无粘结预应力结构影响自振频率的差异,粘结预应力结构自振频率大于无粘结预应力结构。
(3)考虑截面惯性矩的影响讨论预应力线型和偏心结构自振频率的变化时,粘结预应力和无粘结预应力的变化趋势相反,实际工作中应该将两者应该分开考虑。

