提高新能源消纳的电-热综合能源系统 日前优化调度策略

王 森，张照彦，袁玉宝，张东月，成霄楠，石松铠

（1.河北大学电子信息工程学院，河北 保定 071000； 2.河北省智能电网配用电技术创新中心（石家庄科林电气股份有限公司），河北 石家庄 050000）

在我国经济快速发展、能源需求量与日俱增、全球生态环境受损严重的背景下，发展清洁能源产业，推进能源生产和消费革命，构建清洁低碳、安全高效的能源体系，是我国未来能源发展的方向[1-2]。电-热综合能源系统（integrated energy system，IES）可通过电热能量单元与负荷的有机协调降低整个系统的运行成本，同时提升新能源的消纳率，完善新能源规模化开发利用水平。目前，综合能源系统已经成为世界各国能源转型争相发展的重点[3]。

国内外学者已对于电-热IES的日前优化调度进行了研究。文献[4-9]在多方面充分考虑了储能设备在综合能源系统中的影响。文献[10]充分考虑源、荷不确定性对系统的影响，建立了含新能源、电转气设备和多源储能设备在内的IES经济调度模型。文献[11]提出了一种鲁棒协同优化调度模型，以研究综合能源系统与电转气设备协同优化运行问题。文献[12]充分考虑柔性负荷下的虚拟电厂热电联合鲁棒优化调度方法，提高了多种柔性负荷协调优化效果。文献[13]结合各类可平移负荷的特性，分别 对冷热电负荷进行负荷平移，建立了包含经济、环境和能源等多方面运行成本的优化调度模型。文 献[14]建立了考虑柔性负荷的区域综合能源系统储能设备优化配置模型，并采用LINGO商业软件进行仿真分析。文献[15-18]通过对太阳能供热采暖系统的设计及系统优化，为我国太阳能资源高效利用提供了思路。文献[19-20]分析了GLPK的算法原理，并应用其进行了调度问题和区域供能配置的研究。文献[21]利用机会约束来处理风电与负荷的不确定性，验证了气网的动态特性作用。文献[22]基于区间线性规划方法对光伏和负荷的不确定性进行区间描述，建立区域综合能源系统日前经济优化调度模型。文献[23]研究综合能源投资者在计及不确定性因素情况下的投资决策方法，提出一种基于区间线性规划和可逼近理想解排序法的园区型综合能源系统投资决策方法。文献[24]建立了考虑风电与光伏出力不确定性的电气热综合能源系统日前区间优化模型。

综上所述，目前对太阳能集热系统的研究多采用一个独立系统供给热负荷，并未与其他设备相耦合参与调度，而且GLPK作为一个开源的求解器，被用于能源调度求解的例子较少。本文综合考虑新能源不确定性以及需求侧响应的可削减负荷和平移负荷两类柔性负荷与储电、储热单元协调配合，建立了太阳能集热系统与风电机组、蓄电池、蓄热式电锅炉、地源热泵以及生物质锅炉相耦合的电-热综合能源系统日前区间调度优化模型，并在Python程序设计语言环境下运用Pyomo-GLPK对优化模型进行求解；通过算例分析，对比了不同方案的新能源消纳能力、系统运行成本和模型求解速度，验证了本文所提优化策略的有效性。

1 电-热综合能源系统数学模型

电-热综合能源系统结构如图1所示，系统包括风电机组、蓄电池、蓄热式电锅炉、地源热泵、太阳能集热系统以及生物质锅炉。风电机组利用清洁能源风能发电；太阳能集热系统利用太阳能和辅助热源蓄热来提供热负荷；蓄热式电锅炉可以实现电能向热能的转化并储存热量；生物质锅炉作为太阳能集热系统的辅助热源，利用生物质燃料进行制热；地源热泵在电能驱动下利用地热能供热。

1.1 太阳能集热系统

太阳能集热系统采用热管真空管集热器，晴天时集热器吸收太阳能，将蓄热水箱下部进水加热后送入蓄热水箱上部，并将热量储存在蓄热介质中，采暖热水在循环水泵的作用下进入采暖盘管，采暖系统回水进入蓄热水箱底部，如此反复循环将热量传递至室内。夜间或阴雨天时，集热循环泵停止工作，蓄热水箱直接供热，辅助热源在适当的情况下向蓄热水箱补充热量来满足需求。太阳能集热系统结构如图2所示。

本文太阳能集热系统连接室内地板辐射采暖端，地板辐射系统的热媒温度只需40～60 ℃就能满足要求[16]。因此本文设定其回水温度为35 ℃，供回水温差大于5 ℃且小于15 ℃，储热水箱初始水温为40 ℃。

1.1.1 太阳能集热器面积

太阳能集热器面积由以下公式确定[16]：

式中：As为集热器总面积，m2；Qs为1天所需的热负荷；JT为当地日平均太阳辐照，取15.285 MJ/(m2·d)；ηcd为采暖集热器平均集热效率，取60%[16]；ηL为管路及储热装置热损失率，取10%；f为太阳能保证率，应综合考虑当地实际情况来取值，本设计取30%[16]。根据式(1)计算得到太阳能集热器总面积约为2 800 m2。

1.1.2 储热水箱容积

经济研究得出储热水箱的最佳蓄水容积（每平米太阳能集热器面积储水量）是50～100 L/m2。本设计储热水箱的设计容积为75 L/m2×As≈212 m3，因此取水箱体积为220 m3。

1.1.3 太阳能集热器有效输出热量

式中：Qs,t为t时刻太阳能集热系统产热量；Jt为当地t时间段内的平均太阳辐照量；ηd为使用期集热器平均效率，取0.6。

1.2 生物质锅炉

受季节、气候、地点等因素限制，雨雪天或连阴天不能利用太阳能。因此，要保证太阳能系统稳定的热量供应，必须和其他能源的加热设备联合使用，加热设备称为辅助热源。生物质锅炉以生物质能源作为燃料，比传统锅炉效率更高，排烟温度低。生物质能属于可再生能源，合理利用生物质能可以缓解能源危机，减少环境污染，本文选用生物质锅炉作为太阳能集热系统的辅助热源[19]。

生物质锅炉供热的转化模型为：

式中：QBb,t为生物质锅炉在t时间段的产热功率；ηBb为生物质锅炉的热效率，取0.8；βBb为生物质固化燃料发热值，取19 680 kJ/kg；WBb,t为生物质锅炉在t时间段内的使用燃料重量，燃料价格0.7元/kg。

1.3 需求侧响应

柔性负荷的利用是需求侧管理的重要手段之一，需求侧管理通过与需求侧用户签订政策协议给予用户补偿以促使用户根据电价调整用能计划。在这种方式下，将部分刚性负荷转化为柔性负荷，可增强整个系统的协调性，减小用户用电的峰谷差，保证系统运行的安全性和经济性。本文引用可削减负荷和可平移负荷两种柔性负荷。

1.3.1 可削减负荷

可削减负荷为根据用户签订的协议在不影响正常需求的情况下削减其电负荷。负荷削减后时段t的电功率Pper,t,cut为：

式中：Pper,t为用户优化前t时段电负荷；ηt为判断负荷是否发生削减的0-1状态变量；αt为协议范围内的削减比例。

调度后的补偿费用Ccut为：

式中：Ccut,price为协议中单位功率电负荷补偿价格，取值为0.2元/(kW·h)。

1.3.2 可平移负荷

可平移负荷的用电时间连续且时长固定，负荷平移需整体进行。可平移负荷可接受的平移时间区间为t1—t2，当负荷平移到以τ为起始时间的区间内，为保证运行时间连续应满足[14]：

式中：ts为可平移负荷的持续时间，取3 h；mt为判断负荷是否发生平移的0-1状态变量；平移时间区间t1—t2取[3, 22]。

优化后时段t的可平移负荷功率为：

式中：Pshift,t为可平移负荷的额定功率。

调度后给予用户的补偿Cshift为：

式中：Cshift,price为单位功率负荷平移的补偿价格，取0.05 元/(kW·h)。

1.4 新能源不确定性

在区域综合能源系统内，风电出力及太阳能集热受天气因素的影响，其出力预测具有较强的不确定性。在实际系统决策中，获得精确的概率密度函数往往较困难，然而获得不确定变量的取值范围则相对容易，且所需要的信息也会大大减少。由于区间线性规划更适宜处理不确定信息的隶属度函数或分布函数未知的情形。因此，本文利用区间数描述风电出力及光伏产热（－表示区间下限值，+表示区间上限值）从节约成本出发，综合考虑多能互补和网络互济、系统中风电及太阳能产热的预测误差等不确定性因素，建立基于区间线性规划的区域综合能源系统日前经济优化调度模型。

区间线性规划是一种有效处理不确定性问题的方法，它将区间数的理论和方法应用于线性规划中，并且在目标函数或约束条件中含有区间数的一类线性规划。首先，根据实际问题，依据区间线性规划模型一般形式（式(9)）构建优化模型；然后，将构建的模型分解为2个子模型，用最优子模型和最劣子模型代替原模型，通过两阶段分解法分别求得最优值，具体分解方法可参照文献[23-25]得到最优值取值区间，在求解模型过程中需调用Pyomo+ GLPK进行求解。

区间线性规划模型一般形式为：

式中：X表示目标函数的决策变量，即24 h的各设备调度值和交易能量情况A表示不等式约束中X的系数矩阵，A=(aij)m×n，；B表示风电出力及太阳能集热预测区间，表示目标函 数中X的系数矩阵；f表示整个系统的总费用，f= [f-,f+]。

2 电-热综合能源系统日前优化调度模型

2.1 目标函数

考虑需求侧响应和储能的电-热综合能源系统，通过不同设备之间的协调配合在满足用户的负荷需求的同时，寻求整个系统的总运行成本最低。总运行成本包括从电网购电费用、生物质燃料购买费用、弃风惩罚费用、设备运维费用和需求侧响应补偿费用：

其中：

式中：F为系统的总运行成本；Cele为购电费用；Cb为购买生物质燃料的费用；Cwind为弃风惩罚费用；Cyw为能源设备的运维成本；Cbc为柔性负荷补偿成本；λele为分时电价，PBuy,t为t时间段系统从电网购买的电量；λBb为购买生物质燃料单位质量价格；λwind为风电机组的弃风惩罚系数，Ppre,wind,t为风电机组在t时间段的预测产电功率；Pwind,t为风电机组在t时间段的实际用电功率；λj,yw为能源设备j的单位运维成本；Pj,t为t时间段设备j的出力；T为调度总时间段，为24 h。

2.2 约束条件

2.2.1 电功率平衡

整个系统的电力输入和输出应当满足供需平衡，即：

式中：为t时间段用户优化后用电负荷需求；分别表示风电在t时刻的出力上、下限；PREB,t、PHp,t分别为蓄热式电锅炉和地源热泵用电量；PBattery,t为蓄电池出力。

2.2.2 热平衡约束

整个系统的热负荷满足能量守恒定律，即：

式中：Qout,s,t为太阳能集热系统在t时间段的放热量；QREB,t为电锅炉在t时间段的放热量；Qin,s,t和Qout,REB,t分别为蓄热式电锅炉的蓄热体在t时间段的蓄热量和放热量；QHp,t为地源热泵在t时间段的放热量；Qper,t为用户在t时间段需求的热负荷；Ain,t、Aout,t分别为表示蓄热式电锅炉蓄热部分蓄热、放热状态的0-1变量。

2.2.3 蓄热式电锅炉运行约束

蓄热式电锅炉是消耗电力产生热的设备，是系统运行优化的核心设备，同时也是电力系统和热力系统的耦合装置。

1）蓄热式电锅炉产热时的能量转化模型为：

2）蓄热式电锅炉蓄热部分的特性可描述为设备自身容量、输入输出能力、传热效率和热损耗之间的关系，其热传递模型可表示为：

3）为方便管理，蓄热式电锅炉蓄热量周期始末相等：

4）蓄热式电锅炉的不等式约束为：

式中：Pmax,REB,t为蓄热式电锅炉的最大用电功率；Qinmax,REB,t和Qoutmax,REB,t分别为蓄热式电锅炉蓄热部分的最大蓄、放热功率；Smax,REB,t和Smin,REB,t分别为蓄热式电锅炉最大与最小蓄热量。

2.2.4 太阳能集热系统运行约束

太阳能集热系统为集热器和辅助热源相互配合将热量储存在储热水箱，当用户需要时由储热水箱放出热量。

式中：Qoutmax,s,t为太阳能集热系统在t时间内最大放热量；Ss,t和Ss,t+1为t时间段与t+1时间段内的蓄热水箱的蓄热存量；ηsr,in和ηsr,out分别为储、放热效率；Ss,min和Ss,max分别为蓄热水箱的最小和最大蓄热量；、表示太阳能集热器在t时刻的集热上、下限。

2.2.5 生物质锅炉运行约束

生物质锅炉的出力约束为：

式中：Qmax,Bb,t为生物质锅炉在t时间内最大放热量。

2.2.6 蓄电池运行约束

蓄电池作为电储能单元是综合能源系统的重要组成部分，能够有效平抑新能源出力的波动，并实现能量生产与消耗在时间上的解耦，有效解决能量供需不匹配的矛盾。

1）蓄电池出力的数学模型为：

式中：Pin,Battery,t和Pout,Battery,t分别为蓄电池t时间段的输入、输出功率。

2）蓄电池充放功率上下限约束为：

式中：Pinmax,Battery,t与Poutmax,Battery,t分别为蓄电池的最大储、放电功率；Ain1,t、Aout1,t分别为蓄电池充、放电状态的0-1变量。

3）蓄电容量约束为：

式中：SBattery,t和SBattery,t+1分别为t时间段与下一时间段内的蓄电量；ηB,in和ηB,out分别为储、放电效率；Smax,Battery,t和Smin,Battery,t分别为蓄电池的最大、小容量。

4）蓄电池的蓄电量周期始末相等：

2.2.7 地源热泵运行约束

地源热泵设备的数学模型为：

式中：Ccoph为地源热泵的制热能效比。

地源热泵的出力约束为：

式中：Pmax,Hp,t为地源热泵在t时间内最大出力量。

2.2.8 削减负荷约束

可削减负荷的限值约束为：

式中：αmax,t为可削减负荷的上限值，取0.1。

2.3 模型求解方法

模型求解流程如图3所示。建立含有风电和太阳能集热不确定性区间出力的日前区间调度优化模型，将区间模型转换为最优解和最差解的MILP模型，运用Pyomo+GLPK求解。

因模型中存在设备运行状态的二值变量（0或者1）与其出力相乘的非线性耦合关系式，故本文用以下线性化处理方法进行处理[26]。设P(t)为设备出力值，N(t)为设备运行状态的0-1变量。为了对P(t)N(t)线性化，先假定P(t)的上限值为Pmax，增加2个临时变量Q(t)、R(t)。线性化的步骤如下。

1）加入等式约束：

2）加入不等式约束：

经线性化处理后，Q(t)完全等价于P(t)N(t)，但增加了2个变量和3个约束条件。

3 算例分析

本文选取某地算例数据具体分析（算例结构如图1所示），设备包含风电机组、太阳能集热系统、蓄电池、蓄热式电锅炉、地源热泵。以24 h为1个调度周期，单位调度时间为1 h，比较模型在不同场景下的新能源利用情况和总成本。风电机组发电功率预测值、热负荷预测与太阳能集热器集热量预测如图4所示。

算例各时段优化前电负荷构成如图5所示。 图5中：基础负荷为不可优化负荷；可平移负荷是供电时间可按计划变动的负荷，包括洗衣机、消毒柜等；可削减负荷主要是照明灯，可对灯光的使用数量进行削减。

3.1 基础数据

电-热综合能源系统中分时电价如图6所示，各出力设备运行参数见表1，储能设备运行参数见表2。

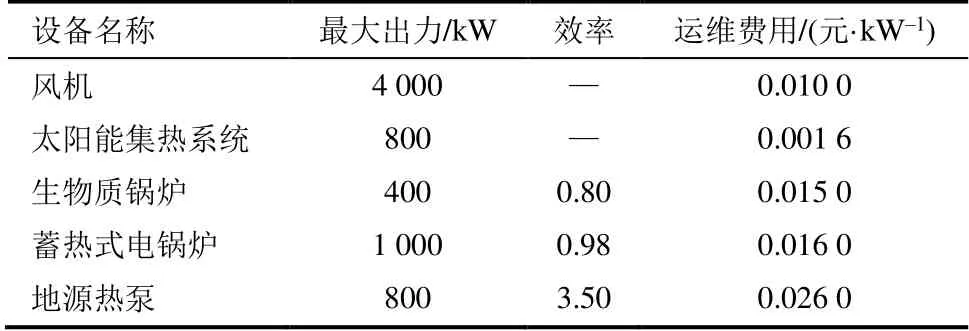
表1 出力设备参数 Tab.1 Parameters of the output equipment

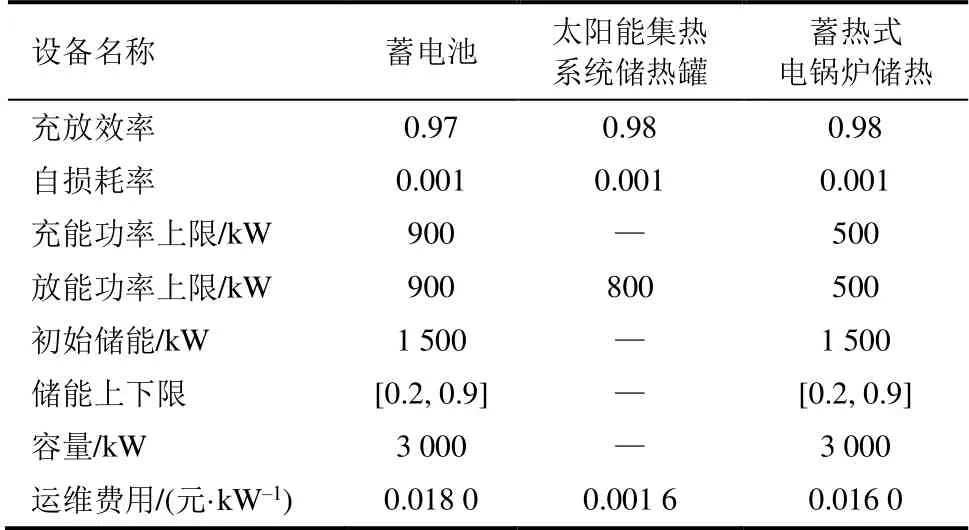
表2 储能设备参数 Tab.2 Parameters of the energy storage equipment

图7为综合考虑电力柔性负荷后电负荷优化前后对比。

由图7可见，在08:00—21:00时段电力负荷均在满足削减条件下进行了削减，缓解了整个系统的供电压力。由图4可知，在00:00—08:00与21:00—24:00 2个时段风电机组发电完全满足用电负荷需求，所以未对其进行削减。对比图6和图7可知，在17:00-20:00时段的3 h，可平移负荷平移到了时段03:00—06:00，以缓解晚高峰的供电紧张，降低了电负荷峰谷差，同时从分时电价的峰时平移到谷时，有利于提高系统经济性。

3.2 不同场景调度结果

为了验证本文所建模型中太阳能集热系统与其他设备的协调利用在优化调度中的影响，设置了以下3种场景。

场景1（S1）：太阳能集热系统与其他设备独立进行供能，考虑风电、太阳能集热的不确定性为5%，运用Pyomo+GLPK进行求解。

场景2（S2）：太阳能集热系统可由地源热泵辅助储热，考虑风电、太阳能集热的不确定性为5%，运用Pyomo+GLPK进行求解。

场景3（S3）：太阳能集热系统与其他设备独立进行供能，考虑风电、太阳能集热的不确定性为5%，运用Yalmip+CPLEX进行求解。

图8—图10分别为S1下最优调度结果的电 负荷、热负荷和太阳能集热系统的出力平衡图， 图11—图13分别为S2下最优调度结果的电负荷、热负荷和太阳能集热系统的出力平衡图。对比S1和S2这2个场景下相应的出力平衡图可知，S1和S2的电负荷出力平衡图相差不大，但因S2中地源热泵可以作为辅助热源对太阳能集热系统进行能量补充，S1和S2的热负荷出力平衡图和太阳能集热系统出力平衡图相差较大。

当00:00—05:00时，风电机组发的电量可以在保证日常负荷需求以及设备约束条件的同时，尽可能多的在蓄电池和蓄热式电锅炉的蓄热体中储存能量。由图8与图11相比可知，S2中地源热泵可以作为辅助热源，因此其所占产热比例比S1多，接近于满负荷运行，且增加了风电的消纳能力。

当05:00—08:00时，虽然风电机组发电量降低，但仍可满足负荷需求。此时蓄电池和蓄热式电锅炉蓄热体的容量已满，为了消纳更多的风电，因此增加电锅炉供热比例。由图13可知，S2中太阳能集热系统储热罐已拥有足够多的能量，因此S2开始使用太阳能集热系统进行供热。

由图8和图11可知，08:00—12:00、16:00—21:00电价峰时段风电机组发电不能满足日常负荷需求，因此优先考虑利用储能装置中储存的能量供给用户需求，在满足负荷要求的同时尽量减少电网购电，以降低系统成本。

12:00—16:00时段为电价平时段，由于储能装置中的能源需优先考虑在电价峰时放出，因此需从电网购电来满足负荷需求，同时还需储存适量能量来供给电价峰时。由图10和图13对比可知，因S2太阳能集热系统提前储存热量，此时比S1的供热量多，S2买电量亦较少。15:00—16:00时，由于S1太阳能集热系统储热不足，需利用地源热泵来供给热量，即购电量相对较多。

由图8和图11可知，21:00—24:00时段需满足储能设备在周期始末储能量一致的约束条件，所以此时供热部分在太阳能集热系统没有多余热量的情况下多选用成本较低的地源热泵来供热。

图14和图15分别为S1和S2的蓄电池和蓄热式电锅炉蓄热体的储能状态变化。对比图14和 图15可明显看出：蓄电池变化曲线差异不大，但S2蓄电池变化曲线较S1的平滑；蓄热式电锅炉蓄热体的差异较明显，S2比S1较为平滑且曲线降低趋势较晚，因此S2的供热承受能力较S1强。

表3给出了3种情景下系统各项成本区间和计算时间。通过对比可知：S2可以有效降低成本和提高对风电的消纳能力；S2比S1的最优调度结果费用降低了17.13%，弃风成本降低了61.75%；而S1中运维费用较低。这是由于S2增加了对地源热泵和太阳能集热系统的使用且风电利用率高，因而设备的运维费用较高。S2中太阳能集热系统和其他供能设备耦合使用，仅小幅增加了设备使用频率，但增加了风电的消纳能力且降低了系统的运行成本。并且由表3可知，本文采用的求解器Pyomo+GLPK，其求解精度和求解速度和常用的求解器Pyomo+CPLEX相差无几，且其可以在多种语言下调用，由于Pyomo+GLPK开源求解器，因此使用相对自由，便于工程运用。

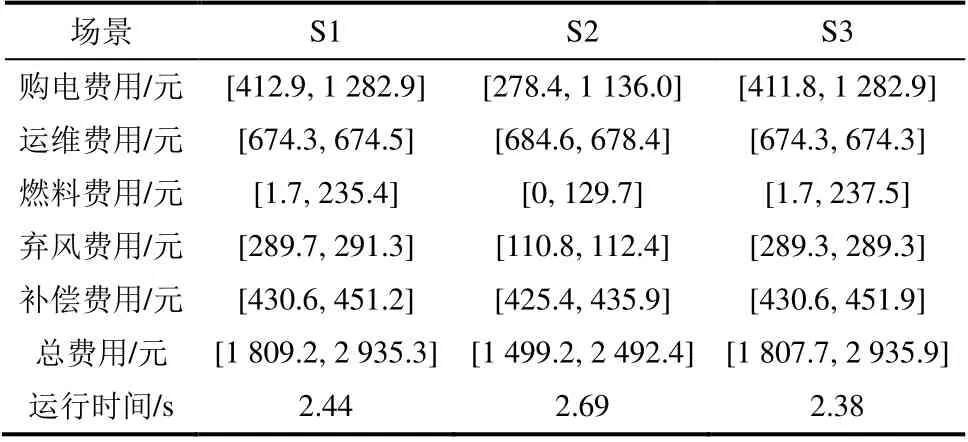
表3 3种场景下系统各项成本区间和计算时间 Tab.3 Operating cost intervals and computation time in three scenarios

4 结 论

1）本文基于MILP模型构建了区间电-热综合能源系统日前调度模型。将地源热泵作为太阳能集热系统的辅助热源，把太阳能集热系统与其他供能设备相耦合进行日前调度，通过Pyomo-GLPK进行建模并求解计算。仿真实例表明，太阳能集热系统和其他供能设备相互耦合进行日前调度，可以在提高新能源消纳能力的同时有效降低系统的运行成本。Pyomo+GLPK的求解精度和求解速度不差于CPLEX，Pyomo+GLPK因其为开源求解器，使用相对自由。

2）本文提出的调度方法相对于太阳能集热系统与其他供能设备独立供能系统，总成本降低了17.13%，弃风成本降低了61.75%，并且增加了系统的供能承受能力。

3）本文所提出的模型对电-热综合能源系统的规划提供了一定的参考。本文主要研究设备间的相互配合，忽略了热网传输以及用户热感知的延时性。因此，在本文所提出模型的基础上，热网传输以及用户感知延时性对系统调度的影响将成为后续研究的重点。