随机变化耦合复杂网络同步与信道衰落估计

刘小斌， 张金南， 侯 男， 董宏丽

( 1. 上海电子信息职业技术学院 中德工程学院，上海 201411； 2. 东北石油大学 人工智能能源研究院，黑龙江 大庆 163318； 3. 东北石油大学 黑龙江省网络化与智能控制重点实验室，黑龙江 大庆 163318； 4. 东北石油大学 三亚海洋油气研究院，海南 三亚 572025 )

0 引言

随控制理论和信息技术的发展，有关复杂动态系统(如传感器网络、多智能体、复杂网络、神经网络)的研究增多[1-5]。复杂网络由一系列相互作用的动态单元组成，包括自然界中的食物网、蜂窝，以及人类生活中的生物网络、交通网络、社交网络等[6-8]。复杂网络的特征是存在网络节点耦合，其动力学行为研究涵盖控制、稳定性、同步与状态估计等问题[9-12]。复杂网络同步可理解为，在初始条件不同的情况下，各个网络节点或子系统通过相互作用使输出趋于接近。复杂网络同步现象常见且重要，如挂在同一个横梁上的两个钟摆通过横梁而相互作用，经过一段时间后自然地出现同步摆动；5G无线通信网络通过各基站间交互信令，实现时钟同步(发射与接收数据的时间基准相同)，保证基站有序传输数据，避免产生强烈干扰而影响正常运转。

状态估计作为复杂网络的另一种动态行为分析，受到人们广泛关注[13-15]。在网络实时监控、故障诊断和工业生产等需要掌握网络行为特征的工程应用中，准确且全面地获取网络节点的状态，是保证设计实现的关键。由于复杂网络规模大、节点耦合强或环境条件恶劣等因素，难以直接获取全部网络节点的状态信息。基于可获得的网络节点的传感器测量信号，在给定性能指标的约束下设计状态估计器，得到复杂网络状态尽可能准确的近似值。如EDWARDS C等提出分布式观测器结构，估计由正时变耦合强度连接的大型半线性网络状态，并应用于互联柔性连杆机器人系统网络，估计电机轴与连杆角位置和速度[14]。

复杂网络的外耦合描述不同节点之间的连接强度或拓扑结构，内耦合反映一个节点内部各状态分量的连接情况[16]，复杂网络的外耦合或内耦合是固定的。当发生链路故障、重建连接、通道阻塞、网络攻击或其他突发现象时，复杂网络的外耦合发生改变；当受到工作条件或环境扰动等影响时，复杂网络的内耦合发生改变，可能对复杂网络的性能产生作用[17]。在复杂网络的性能分析过程中，考虑耦合变化可以有效保证研究的现实性及有效性。有关复杂网络的不固定外耦合和内耦合的研究包括切换拓扑[18-19]、时变拓扑[20-21]、马尔可夫切换拓扑[22]、不确定内耦合[23]、时变内耦合[24]及随机内耦合[25]等，其中马尔可夫链通过转移概率反映模态切换，是典型的随机切换模型，用来描述复杂网络的随机变化耦合强度现象。

随网络通信的产生，在信号传输网络为生产提供便利的同时，通信信道带宽有限等物理条件易引发多种网络诱导现象[26-28]。特别是当信号通过无线通信信道传输时，受地理位置或障碍物影响而引起反射和衍射，导致接收到的信号包含来自不同路径的信号分量。在接收端，各路径信号分量的到达时间和相位不尽相同，与原信号相比，它们迭加后导致信号振幅变化和延迟，降低信号的质量和精度，称为多路径衰落[29-30]。相较于使用理想测量信号，使用信道衰落信号设计估计器更加反映真实情况。人们在信道衰落研究方面取得进展[31-33]，如SHEN Y等引入Rice衰落模型，描述传感器测量信号经由衰落信道传输至滤波器时，随机发生数据缺失及延迟，为克服测量信号的时滞项给数学推导带来影响，设计递归滤波器。

在复杂网络系统的实际使用过程中，发生元件老化和工作条件差异等现象，使系统的模型参数具有时变特性[34-35]。引入时变参数可以较准确地描述系统的动态演变，提高研究的可靠性和应用有效性。复杂网络系统也受到环境的随机突变、部件故障或子系统互联等扰动，直接影响系统的状态和动态性能。为避免建模理想化，在状态中考虑乘性噪声和加性噪声以反映存在的扰动[36-37]。实际系统一般还具有非线性特性，在复杂网络系统分析与综合研究过程中，不可缺少对非线性的处理[38-39]。因此，非线性时变复杂网络的同步及信道衰落估计，是符合工程需要和亟待解决的基础研究课题。

首先，介绍一类贴合实际的具有乘性噪声和加性噪声的时变离散复杂网络系统模型，复杂网络系统的拓扑连接和内耦合连接强度随机变化，随机性由马尔可夫链刻画，模态按照转移概率随机切换。其次，分析系统的同步性能和设计复杂网络H∞同步方法。再其次，基于更为一般化的复杂网络模型，考虑实际测量传输时产生数据随机缺失和延迟等，采用信道衰落的数学模型反映信息不完全现象，设计基于信道衰落的H∞状态估计器；借助于计算递归矩阵不等式确定H∞估计器增益。最后，通过两个仿真实例说明设计方法是可行的。

1 问题描述

在有限域[0,N0]上，考虑节点个数为Λ的复杂网络系统。节点i(i=1,2,…,Λ)动态：

(1)

式中：xi(k)和zi(k)分别为节点i的状态向量和输出向量；ϑj(k)符合标准正态分布，即ϑj(k)～N(0,1);若γjq(k)≠0，则Γq(k)diag{γ1q(k),γ2q(k),…,γrxq(k)}≥0为连接第j(j=1,2,…,rx)个状态变量的内耦合矩阵；v(k)表示干扰；A0(k)、B0j(k)(j=1,2,…,a)、Gi(k)和E0(k)为已知且维数恰当的参数矩阵；非线性向量函数h(·)(h(0)=0)遵循约束条件：

[h(x)-h(y)-H1(x-y)]T[h(x)-h(y)-H2(x-y)]≤0,∀x,y∈Rrx,

(2)

式中：H1和H2为给定矩阵。马尔可夫链q(k)(k≥0)在一个有限状态空间{1,2,…,U}中取值。给定转移概率矩阵Δ[πmn]U×U中的各个元素：

Prob{q(k+1)=n|q(k)=m}=πmn,∀m,n∈{1,2,…,U}，

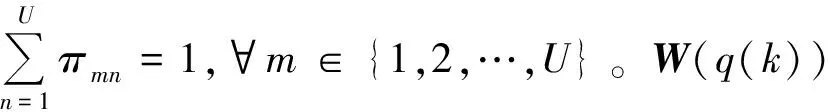
注1受环境干扰或元件老化等影响，复杂网络内部动态可能出现随机特性。采用马尔可夫链刻画复杂网络的随机变化耦合[19,22]，并考虑乘性噪声开展分析。

(3)

成立，那么离散时变复杂网络系统为全局同步。

2 同步分析

(4)

定理1在引理1情形下，如果存在常数c>0和矩阵Qm(k)>0，在初始条件

(5)

下，可保证递归矩阵不等式

(6)

成立，那么离散时变复杂网络系统(1)为全局渐近同步，其中，

证明根据式(1)，可得xi(k)(i=1,2,…,Λ)的紧凑表达形式：

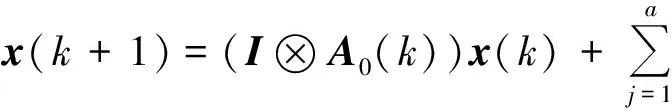
h(x(k))+(Wm⊗Γm)x(k)+G(k)v(k)。

(7)

为简便处理时变复杂网络(7)的同步问题，选择函数：

(8)

式中：

(9)

(10)

定义符号xir(k)xi(k)-xr(k)和hir(k)h(xi(k))-h(xr(k))。

由约束条件(2)可得

(11)

借助于引理1并根据式(10)和(11)，可得

(12)

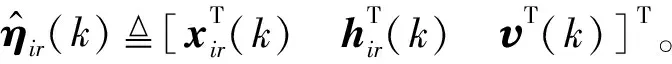
考虑式(6)，可得

(13)

对式(13)两边关于k由0至N0求和，可得

进而可得

根据式(5)，式(3)成立。

注2受环境噪声影响，在存在本质非线性等工程的实际情况下，建立具有时变参数、随机变化耦合、非线性、乘性噪声和加性噪声的复杂网络系统(1)。在定理1中，给出使时变复杂网络(1)实现同步的充分条件。计算递归矩阵不等式(6)的解集，使复杂网络各个节点的输出之差符合H∞性能指标要求，即在任何干扰存在的情况下，不同节点的输出之差仍低于给定的扰动衰减水平。

3 估计器设计

基于式(1)，考虑表达形式更为一般的复杂网络节点状态估计：

(14)

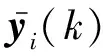
在传感器测量信号经由通信网络传输至接收装置(估计器)的过程中，发生信道衰落现象，使实际被接收到的信号不再是原测量信号，而是来源于多路径且有强度差异的各信号分量相迭加。采用数学表达形式描述信道衰落信号：

(15)

注3不充分信息现象一方面来自于传感器本身的特性(传感器非线性、量化、饱和、传感器分辨率引起的不确定性)，另一方面来自于测量信号经由网络传输过程中受外部环境和扰动等因素的影响，使原信号发生失真(信道衰落、测量丢失、误码、数据包错序)。在信道衰落信号(15)中，被接收的信号为来自多个不同路径的子信号的迭加。区间[0,1]上，按照概率密度函数随机取值的信道系数，反映各个信道中信号幅值的衰减。测量信号时滞描述由不同传输路径的传输距离带来的通信延迟。当ε=0，δis(k)=1且Li(k)=0时，式(15)与理想测量信号相同。

基于信道衰落信号(15)，采用时变状态估计器得到复杂网络(14)各节点的状态估计：

(16)

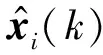
定义OmO(q(k))(O=Γ,ωir,Ki(k))和令和分别描述状态与输出的估计误差。由式(14)和(16)可得：

(17)

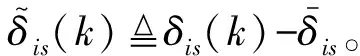
为了数学表示简便，定义变量：

X(k)diag{X1(k),X2(k),…,XΛ(k)}(X=A,C,E),Bj(k)diag{B1j(k),B2j(k),…,BΛj(k)},

根据式(14)和(17)，可得xi(k+1)、ei(k+1)和zei(k)的紧凑形式：

(18)

(19)

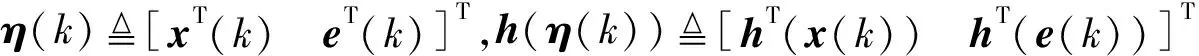
(20)

设计复杂网络(14)的时变状态估计器(16)的增益参数，使增广估计误差动态系统(20)满足H∞性能指标要求：

当k=-ε,-ε+1,…,-2,-1时，η(k)≠0,

(21)

式中：γ为已知的干扰抑制水平；Zζ(ζ=-ε,-ε+1,…,0)为已知的正定矩阵。

分析增广估计误差动态系统(20)的有限域H∞性能，给出时变状态估计器(16)的存在条件。利用递归矩阵不等式方法计算估计器(16)的未知增益。

定理2给定干扰抑制水平γ>0及估计器增益参数Kim(k)(i=1,2,…,Λ)。如果存在正定矩阵Rm(k+1)>0，Pv(k)>0(v=1,2,…,ε)及正常数t，在初始条件

(22)

下，满足不等式：

(23)

那么增广估计误差动态系统(20)满足H∞性能指标要求，其中，

证明定义函数：

V(k,η(k),q(k))V1(k,η(k),q(k))+V2(k,η(k)),

(24)

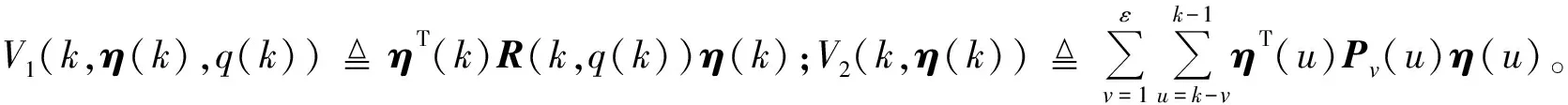
为简化表达，令Rm(k)R(k,q(k)=m)，计算V(k,η(k),q(k))的差分的数学期望：

E{ΔV1(k,η(k),q(k))}=E{V1(k+1,η(k+1),q(k+1)=n)|η(k),q(k)=m}-V1(k,η(k),m)=

ηT(k)Rm(k)η(k)。

(25)

式中：

(26)

考虑非线性约束条件(2)，可得

(27)

则得

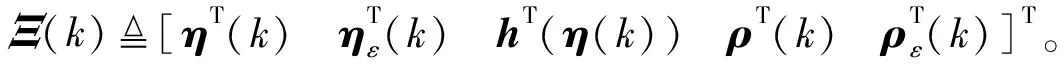
根据式(23)和初始条件(22)，可得式(21)成立。

讨论时变H∞状态估计器(16)的增益参数Ki(k,q(k))的求解方法。

定理3给定干扰抑制水平γ>0。若存在正定矩阵Rm(k+1)diag{R1m(k+1),R2m(k+1)}>0(R1m(k+1)diag{R11m(k+1),R12m(k+1),…,R1Λm(k+1)},R2m(k+1)diag{R21m(k+1),R22m(k+1),…,R2Λm(k+1)})，Pv(k)>0(v=1,…,ε)，矩阵Φm(k)diag{0,Φ2m(k)}(Φ2m(k)diag{Φ21m(k),Φ22m(k),…,Φ2Λm(k)})和正常数t，在初始条件下，满足递归矩阵不等式：

(28)

则增广估计误差动态(20)达到H∞性能指标要求(21)，其中，

状态估计器(16)的增益参数为

证明式(23)与不等式等价：

(29)

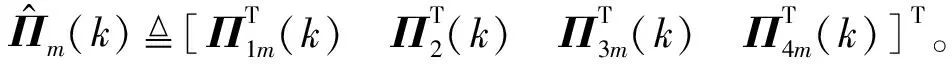
根据Schur补引理，可得

(30)

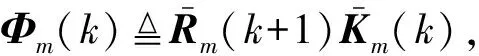
时变状态估计器(16)的设计算法：

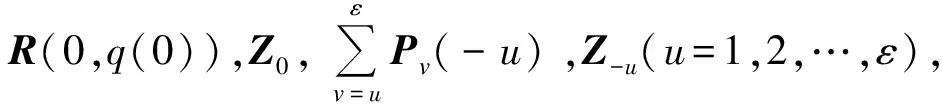
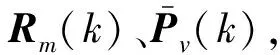
步骤4结束。

注4基于定理2的H∞性能分析结果，在定理3中，对时变复杂网络(14)提出有限域H∞状态估计器(16)的设计方法。由递归矩阵不等式(28)可知，估计器设计方法形式简单，易于实现。采用定理3的算法，可以在估计误差达到H∞性能指标要求(21)下，通过计算递归矩阵不等式的解，求出估计器(16)的增益参数，可得复杂网络(14)的节点状态的近似值。在有限域H∞性能指标(21)的约束下，即使面对强烈噪声，估计误差也被限制在给定的干扰衰减水平下。定理3结果包括复杂网络系统的时变参数、非线性约束条件中的矩阵、描述随机变化耦合强度切换的马尔可夫链转移概率、信道系数的均值和均方差。

4 仿真实例

例1考虑有限域[0,30]，选择复杂网络(Λ=4)的参数：

给出非线性函数

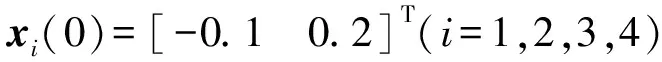
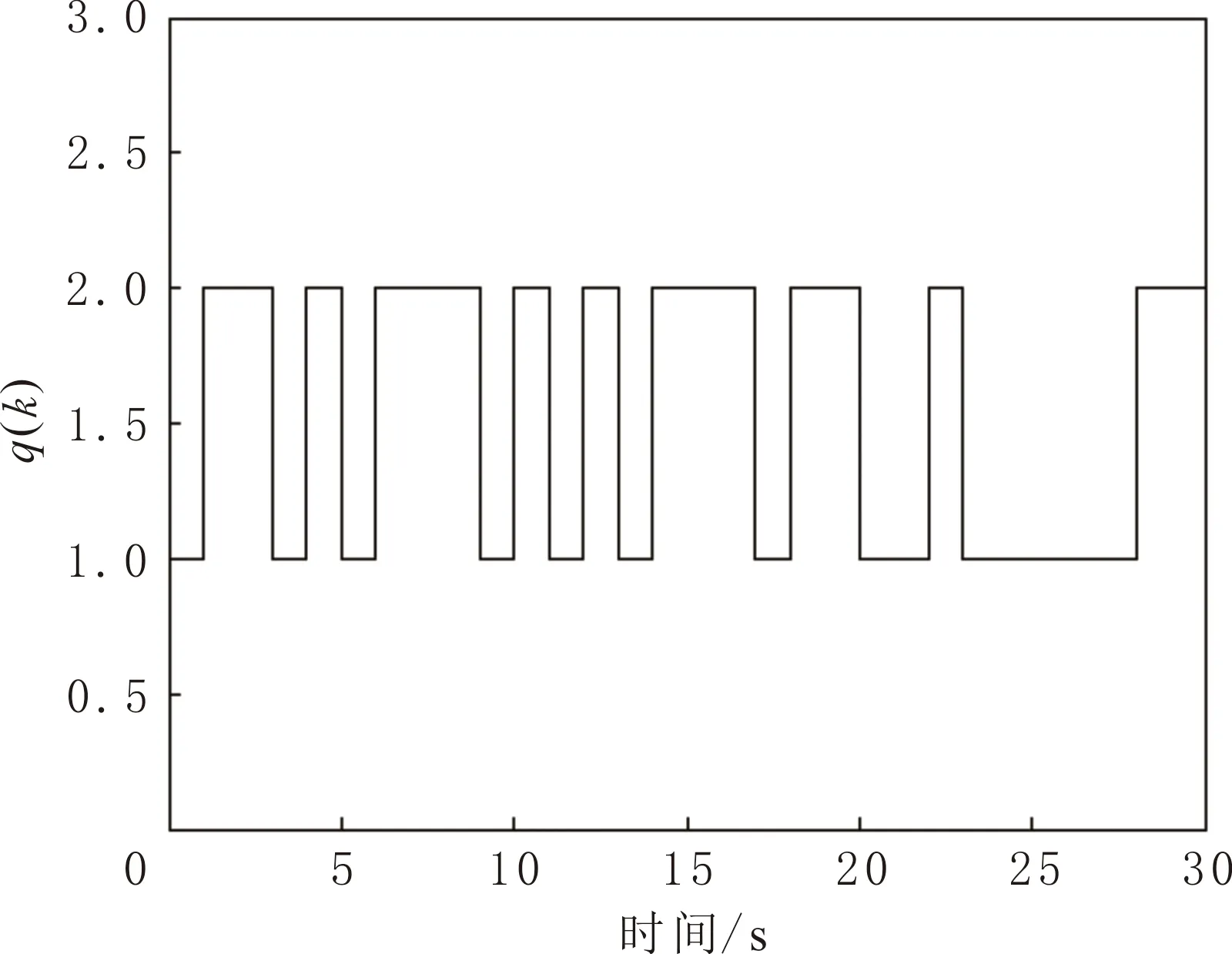
图1 仿真实例1模态切换Fig.1 Mode switching of simulation example 1

图2 仿真实例1复杂网络同步误差Fig.2 The synchronization error of complex network in simulation example 1

图1为马尔可夫链q(k)在转移概率矩阵Δ下，随时间在2个模态q(k)=1和q(k)=2之间的随机切换情况。图2为节点1的输出z1(k)分别与其余3个节点的输出z2(k)、z3(k)、z4(k)之间的同步误差曲线。由图2可知，在第0～13 s之间，节点1和节点2的最大同步误差是0.010，节点1和节点3的最大同步误差是0.026，节点1和节点4的最大同步误差是0.045；从第14 s开始，节点1与其余3个节点之间的输出同步误差开始趋于0。

例2在有限域[0,30]上，选择复杂网络(Λ=4)的参数：

其他参数和非线性函数的选择见例1。

关于信道衰落信号(15)，给出ε=2，选择信道系数的概率密度函数：

表1 仿真实例2的时变状态估计器增益参数

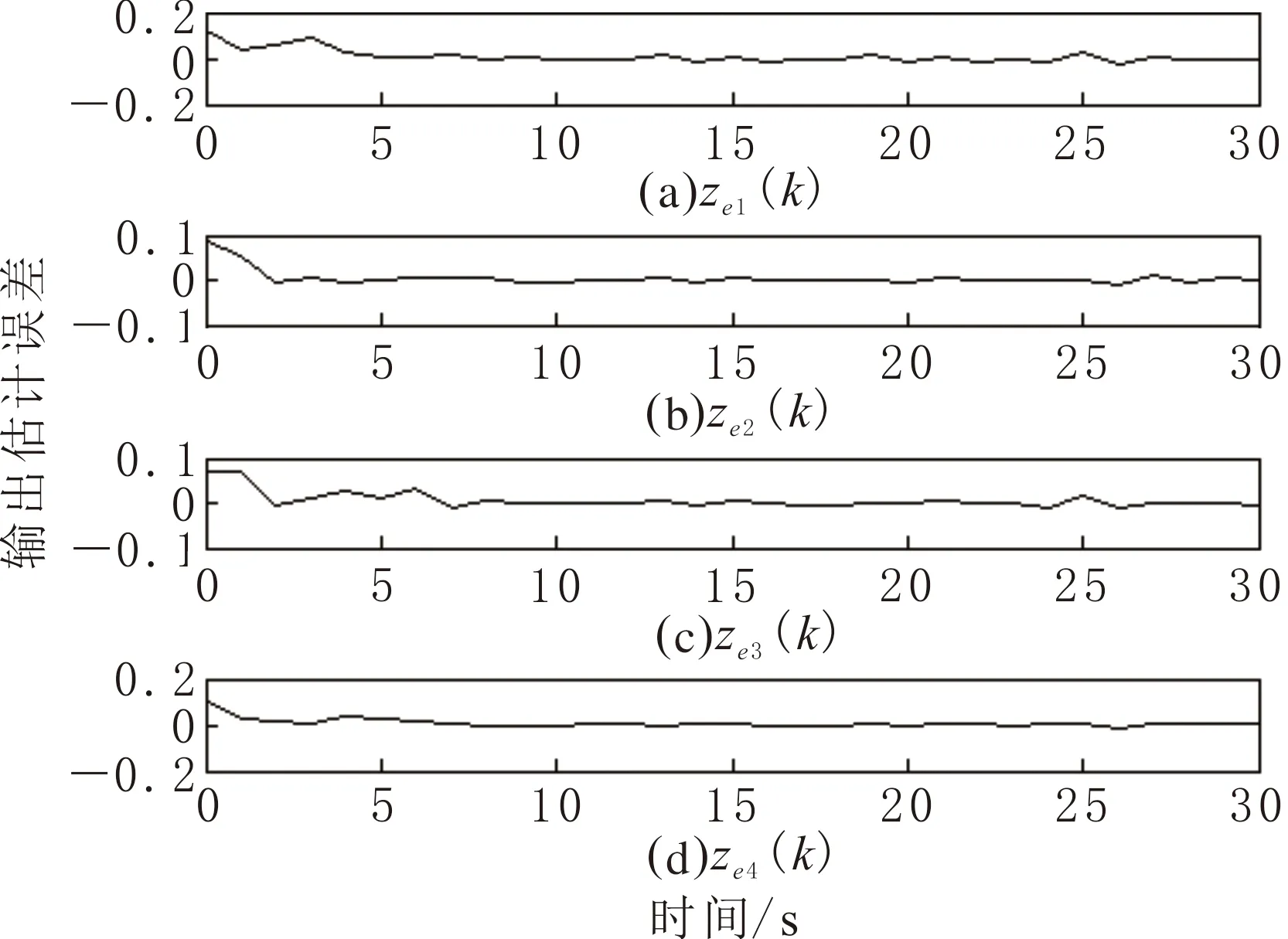
图3 仿真实例2输出估计误差Fig.3 Output estimation error of simulation example 2

图4 仿真实例2估计性能Fig.4 The estimation performance of simulation example 2

5 结论

(1)对于考虑时变参数、随机变化耦合、非线性、乘性噪声和加性噪声的复杂网络系统，设计H∞同步方法与基于信道衰落的H∞状态估计器。

(2)分别基于复杂网络的有限域同步与估计性能分析，以递归矩阵不等式表示使同步误差与估计误差具有H∞性能的充分条件。

(3)仿真实例证明设计方法具有有效性，复杂网络达到H∞同步，并且设计的状态估计器使得估计误差系统满足H∞性能要求。在后续研究中，将基于部分网络节点的测量，讨论具有网络诱导现象的复杂网络非脆弱性状态估计。