压缩感知下最短路径的无线网络数据收集算法

魏连锁， 马敬云， 郭 媛

( 齐齐哈尔大学 计算机与控制工程学院,黑龙江 齐齐哈尔 161006 )

0 引言

无线传感器网络(Wireless Sensor Networks, 简称WSNs)[1-4]是由大量传感器节点组成，对数据进行收集、处理、传输的一个无线自组织网络。由于传感器节点的铺设成本与功耗日益降低，WSNs在数据收集[5-7]、海洋环境监测等方面的应用价值越来越大[8]。同时，数据收集是WSNs各个应用中数据通信不可或缺的重要环节，参与数据收集的数据通常具有一定的稀疏性，可将压缩感知(Compressed Sensing, 简称CS)[9-10]稀疏随机投影技术应用于WSNs数据收集过程。由于传感器节点能量有限且不能及时更换，减少投影过程的节点能耗成为WSNs数据收集和处理的关键。目前，对WSNs数据收集过程主要针对数据包的收发能耗，采取有效途径使数据收集过程中的数据包数目减少，可有效减少网络能耗。存在问题：(1)压缩处理数据时，采取数据先收集后压缩的方式，对资源受限的无线传感器网络造成资源浪费；(2)数据传输过程中，未考虑节点多跳通信与网络数据处理，而是将节点收集数据包直接发送至汇聚节点。因此，在设计算法时，对数据处理以减少网络节点能耗是WSNs数据收集算法需要考虑的因素。

人们提出多种将压缩感知(CS)应用于WSNs数据收集的算法，如BAJWA W U等[11]将CS技术应用到WSNs数据收集过程，在数据的传输过程中未进行数据处理，而是将收集到的数据直接发送给汇聚节点，网络能耗由于参与数据收集的节点数目冗余而过大。在降低节点数据量方面，较多将稀疏投影应用于WSNs数据收集，如杨浩等[12]提出区域化的压缩感知数据收集算法，将压缩感知稀疏随机投影矩阵引入WSNs数据收集，对每部分单独压缩，解决数据收集过程中数据量过大的问题，但稀疏投影矩阵的设计过于复杂；WU C等[13]提出的基于CS减少数据冗余的WSNs数据收集算法，稀疏随机投影矩阵的建立相对简单，采用网格编码的形式降低数据的冗余度，但算法中冗余数据的数目过大，造成过多的网络能耗。

文献[11-13]的WSNs数据收集算法主要集中于数据传输的方式而忽略网络能耗，真实的WSNs数据收集算法过程产生大量能耗，人们提出多种解决方案，如CHOU C T等[14]提出的算法综合考虑节点能耗问题，以较小的能耗获取收集的节点数据，在数据收集效果较好的情况下减少网络能耗，但算法需要交换信息的节点数目较多且采用的是穷举法，复杂度过大，只能用在小型无线传感器网络中；VELMANI R等[15]提出的算法可应用在大型无线传感器网络中，但恢复原始数据需要收集的节点数目随网络规模的变大而增加，网络能耗随之变大。

将压缩感知稀疏随机投影矩阵与WSNs数据收集过程相结合，设计能耗低、网络负载均衡的WSNs数据收集算法具有重要意义。WSNs数据收集算法需综合考虑数据通信节点数量对网络能耗的影响，同时避免因观测数过少而导致重构误差变大的问题。笔者综合考虑节点能耗、重构误差等因素，采用压缩感知稀疏随机投影技术，提出低能耗、误差小的无线传感器网络数据收集算法，为WSNs数据收集方案的发展提供思路。

1 系统模型

1.1 压缩感知模型

根据压缩感知理论，当原始信号由某个稀疏矩阵稀疏化时，可通过一个投影矩阵将稀疏信号投影为低维列向量，求解一个凸优化问题，重构出原始信号。其中，投影矩阵的制定必须符合有限等距约束条件(Restricted Isometry Property,简称RIP)[16]，即

(1)

式中：当δK∈(0,1)时，矩阵Φ满足K阶约束等距，即可近似地重建原始信号矩阵X，X=[x1,x2,…,xn]N，为N维原始信号。

在压缩感知投影矩阵过程中，投影矩阵Φ的稀疏度越高，消耗的能量越少。目前，投影矩阵研究大多是在投影次数和重构算法上对基于压缩感知的投影机制做优化，采用稀疏投影观测矩阵[17]减少单个投影值产生的损失。稀疏随机投影矩阵表达式为

图1 基于压缩感知的稀疏随机投影数据收集过程Fig.1 Sparse random projection data collection process based on compressed sensing

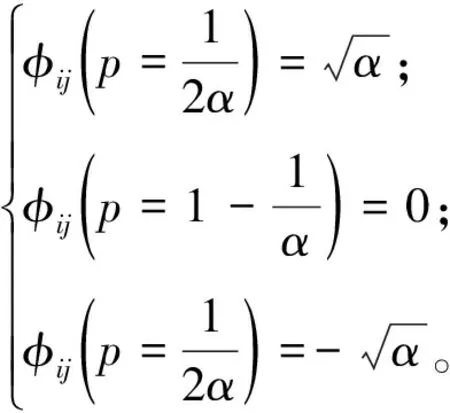
(2)

式中：φij为随机投影因数；p为φij取相应值时的概率；α为投影矩阵的稀疏程度。

稀疏投影过程：首先，生成稀疏投影矩阵，在每次投影过程中节点i从投影矩阵的第i行中选择出φij≠0的节点；然后，投影节点根据路径选择策略获取节点数据，将投影节点本身的数据与感知节点传递的数据融合后，再通过路径选择策略传递给Sink节点，汇聚节点从这些节点中任意选取m个节点的数据；最后在Sink节点处通过m个观测值重构原始信号。基于压缩感知的稀疏随机投影数据收集过程见图1。图1基于稀疏投影的一次数据收集过程，参与投影过程的节点为1、3、7，则融合数据为

y1=φ11x1+φ13x3+φ17x7,

(3)

式中：xi为节点收集数据。转换为矩阵形式，即

(4)

原始信号X的重构过程是指通过一定的重构算法，将原始信号稀疏化后的低维观测向量再重构为X。通过求解最小l0范数实现，但l0范数的求解为非确定性多项式(Nondeterminism Polynomial, 简称NP)问题，可将之转化为最小l1范数[18]求解得出，即

(5)

s.t.ΦX=y,

求解过程为一个线性优化问题，可以运用贪婪迭代算法求解；采用正交匹配追踪(Orthogonal Matching Pursuit, 简称OMP)算法[19]作为信号重构算法。

1.2 数据收集模型

在能量有限的无线传感器网络中，节点能耗过大导致网络陷入瘫痪，因此减少网络能耗，以最少的能耗实现数据有效收集是关键。将CS与路径选择策略相结合引入数据收集过程，可解决节点信息冗余对网络资源带来的浪费及数据冲突造成信息收集效率低等问题。

由n个传感器节点组成的无线传感器网络模型见图2。由图2可知，在数据收集过程中，使用的数据传输信道为无线信道，由传感节点、感知节点、投影节点、汇聚节点构成。在第i轮数据收集过程中，随机选取m个节点进行数据收集传输至汇聚节点，其表达式为

yi=ΦX+λ=φi1x1+φi2x2+…+φimxm+λi,

(6)

式中：yi为m个节点传输至汇聚节点的融合数据矩阵；φim为随机投影矩阵Φ的第i个列向量；xm为节点收集数据；λ为噪声矢量，在不考虑噪声的情况下为0。

图2 n个传感器节点组成的无线传感器网络Fig.2 Wireless sensor network composed of n sensor nodes

图3 基于压缩感知的数据收集机制Fig.3 Data acquisition mechanism based on compressed sensing

由式(4)将图3转换成矩阵的形式，即

(7)

式中：

(8)

传统的稀疏投影模型先将数据传递到某个投影节点后再传递给汇聚节点，但有较多的节点到汇聚节点的距离小于到投影节点的距离。若继续按照传统的稀疏投影进行数据传输，增加数据传输过程的数据量，产生的能耗也大，故直接将此类节点传输到汇聚节点，然后与投影节点传到汇聚节点的数据融合处理。相较于传统的稀疏投影模型，可使基于最短路径树的数据收集模型中参与节点的数量显著降低，产生的网络能耗有效减少(见图4)。

图4 基于压缩感知的最短路径树数据收集过程Fig.4 Shortest path tree data acquisition process based on compressed sensing

1.3 能耗模型

在无线传感器网络数据收集过程中，数据处理所需能耗远小于数据收发能耗，因此主要考虑数据收发能耗，忽略影响不大的因素(节点数据处理的能耗等),建立能耗模型。应用文献[20-21]的通信能耗模型，假定两个节点间的距离为d，发送的数据包长度为b，则任一节点发送数据的能量消耗表达式为

Et(b,d)=Ee×b+b×εad2,

(9)

Er(b)=b×Ee,

(10)

式(9-10)中：Et(b,d)为将长度为b的数据发送距离d需要的能耗；Ee为发送能耗因数；εa为能耗放大因数；Er(b)为数据接收能耗。

根据式(7)改进能耗模型，将路径损失考虑在数据收集的过程中。若在一次数据收集的过程中，一共有m个节点参与，则Et(b,d)表达式为

Et(b,d)=m[Ee×b×A(d,f)+b×εad2]=

(11)

式中：

A(d,f)=dk·a(f)d,

(12)

(13)

式(12-13)中：A(d,f)为路径损失函数；dk为损失因数；f为信号频率；k为路径损失指数(在实际应用中，通常取1.5)；a(f)为吸收因数。由式(12-13)可以看出，数据传输距离d越大，路径损失A(d,f)越大，能耗Er(b,d)越多。

节点接收数据的能量消耗表达式为

Er(b)=m(b×Ee),

(14)

式中：Er(b)为数据接收能耗。

总体上，除了数据收发能耗以外，传感器节点数据的处理及寻找最短节点等也产生一定的能量消耗，但收发能耗较小时，这部分将不纳入总体能耗计算。总能耗Etl可表示为

(15)

2 算法实例

2.1 步骤

步骤1对数据进行初始化和预处理。依据节点在网络中的位置对节点执行一维化操作，将数据转化到一维空间进行处理。

步骤2获取节点的邻接矩阵，通过最短路径算法(Dijkstra算法)分别将网络中各个节点到节点的最短路径与最短距离计算出来。

步骤3根据式(2)生成稀疏投影矩阵Φm×n=[φ1,φ2,…,φn]，其中φi(1≤i≤m)为每一个数据包的随机投影因数，将其加入投影节点集合Ui={Ui(1),Ui(2),…,Ui(lgn)}。从Φm×n中选取非零元素对应的节点加入感知节点集合Γi={Γi(1),Γi(2),…,Γi(n/m)}；随机从感知节点集合中选取一个作为投影节点，根据步骤2得到各个节点到汇聚节点的最短路径，生成一个最短路径树集合。此外，矩阵的行数由获取数据包的数量m决定，且每一行代表一条传输路径。

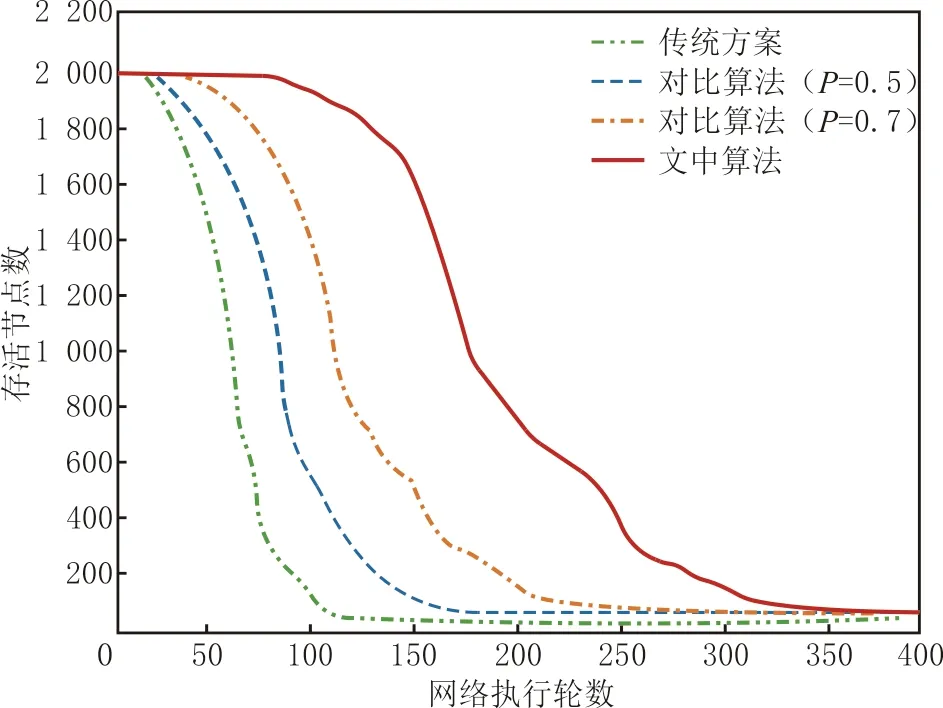
步骤4对参与传输的节点进行判断。若节点到Sink节点的距离dSink小于投影节点的距离dUi，即dSink

步骤5重复对步骤4执行m次，Sink节点得到可以恢复数据的所有m个测量值，再汇聚节点进行信息重构。

步骤6若不同的投影节点在传输过程中某一节点处开始重合，则在该结点处先将数据融合再传输。

算法伪代码见表1。

表1 算法伪代码

续表1

2.2 算法时间复杂度分析

算法的复杂度是衡量一个算法计算量的重要指标。文中算法的核心是数据的传输部分，主要包含路径选择和数据转发两个阶段。数据转发的时间复杂度为O(1)，路径选择策略的时间复杂度为O(n2)，故文中算法的时间复杂度为O(n2)。

3 算法仿真与分析

以python语言为工具，在pycharm集成开发环境下进行算法仿真实验，并对无线传感网中节点的能耗及存活量与对比算法[22]进行对比分析。该实验将CS与最短路径结合应用于数据收集过程，数据收集效率提升，网络能耗显著降低，网络生命周期变长。

3.1 参数设置

算法仿真实验的相关参数设置见表2。

表2 算法仿真参数设置

3.2 实验结果

通过三个标准全方位、多角度分析算法的性能，即

(1)重构误差；

(2)网络节点最大能量消耗；

(3)网络生命周期(按照执行轮数，以网络中出现第一个死亡节点作为一个生命周期)。

实验中，采用重构误差τ对重构效果进行评价，表达式为

(16)

式中：

(17)

(18)

(19)

首先，就算法对信号的重构效果进行仿真分析。文中算法与对比算法的重构误差随观测数变化的曲线见图5。仿真结果表明，对于观测数的不同，重构误差有所不同，随观测数增加，信号的重构质量呈递增趋势。算法的重构误差随观测数增加而逐渐降低，在观测数相同的情况下，文中算法的重构精度高于对比算法的。

图5 观测数与信号重构质量的关系Fig.5 The relationship between observed quantity and signal reconstruction quality

重构质量的对比关系见图6。由图6可知，在相同的观测数下，文中算法的重构误差小于对比算法的。原因在于投影过程中，文中采用的是稀疏投影矩阵，而对比算法采用的是密集矩阵。与对比算法相比较，信号的稀疏度越高，数据的重构误差下降越慢，数据的重构质量越高，文中算法对信号的重构有较好的效果。

图6 重构质量的对比关系Fig.6 Comparison relationship of reconstruct quality

不同算法网络执行轮数与节点最大能耗的关系见图7。在数据传输过程中，采用稀疏随机投影矩阵，在数据的传输阶段只进行信息中转与信息传输操作，并不执行数据融合；在数据传输过程中，对比算法采用密集投影矩阵，在数据融合阶段仅对节点数据简单迭加。由图7可知，随网络执行轮数的增加，节点的能耗呈递增趋势。在网络执行轮数相同时，节点的最大能耗由高到低依次为传统方案、对比算法与文中算法，且文中算法的能耗最小。同时，在文中算法中，当网络执行到第55轮时，出现首个死亡节点，相较于对比算法(P=0.5，P为节点接入概率)，明显延长网络寿命，使网络生命周期增加6轮；与对比算法(P=0.7)算法相比，网络生命周期增加20轮，而传统方案在网络执行到第25轮时出现首个死亡节点。在能耗方面，文中算法相较于传统算法既节约网络能耗，又延长传感器网络的生存周期，具有较好的性能。

图7 不同算法执行轮数与节点最大能耗的关系Fig.7 The relationship between the number of rounds executed by different algorithms and the maximum energy consumption of nodes

网络执行轮数与存活节点数的关系见图8。由图8可知，在网络执行的初始阶段没有死亡节点出现；随网络执行轮数的增加，网络的节点能耗逐渐增大，网络开始出现死亡节点，存活节点数逐渐减少。文中方案延长网络的生命周期，其中，传统算法在执行到第29轮时，出现首个节点因能量耗尽而死亡，而对比算法的次之。文中算法在执行到第79轮时，最晚出现死亡节点，与对比算法相对比，网络的生命周期延长约2倍。传统算法出现死亡节点的时间最早，节点的死亡速率最高，但随网络执行轮数越来越多，存活节点数目减少，死亡速率又趋于平缓。文中算法在初期节点死亡速率最低，随执行轮数的增加，节点死亡速率增大后又趋于平缓。因此，文中算法的死亡节点出现的时间最晚，节约网络能耗效果良好。

图8 网络执行轮数与存活节点数的关系Fig.8 The relationship between the number of network execution rounds and the number of viable nodes

3种算法的节点广播半径与网络能耗比的关系见图9。由图9可知，随节点广播半径的增加，网络能耗比逐渐上升；在广播半径相同的情况下，传统算法的能耗比例最高，对比算法的次之，文中算法的能耗比最低，效果最好。因此，文中算法可有效延长网络寿命，解决数据收集能耗问题。

图9 节点广播半径与网络能耗比的关系Fig.9 The relationship between node broadcast radius and network energy consumption ratio

4 结论

(1)基于稀疏随机投影压缩感知下最短路径的无线网络数据收集算法与对比算法相比，在保证原始数据重构精度的前提下，能够减少数据收集过程中的数据量，降低能耗；提出根据自身收集信号强度调节选择数据发送概率机制，延长网络寿命。

(2)文中算法为稀疏投影压缩感知下的无线传感器网络的数据收集提供一种新的解决方案。