k-means 聚类分析算法在人工智能+个性化学习系统中的应用

浦慧忠

（无锡城市职业技术学院，江苏 无锡 214153）

0 引言

通常情况下，人们在逛电商网站时都会收到一些推销活动的通知，但该客户之前并没有关注过那些商品。那么，这些电商网站是依据什么决定给客户推销该商品的呢？究其原因就在于电商网站会根据用户的年龄、性别、地址以及历史数据等等信息，将其分为：“年轻白领”、“一家三口”、“家有一老”、”初得子女“等类型，在此基础上就会根据用户的特征类型，向其推送不同的优惠活动。研究中，利用这些数据将用户分为不同的类别时，就会用到聚类分析。

研究可知，聚类就是将一个数据集划分为若干组或类的过程。通过对数据进行分组（目的），若组内的相似性越大、组间的差距越大，聚类效果就越好（评价标准）。而聚类分析就是致力于发现这些数据对象之间的关系，期寄在相似的基础上收集数据来分类。聚类大多是应用在数据挖掘、数据分析领域，并属于机器学习中非监督学习的范畴。目前，已经比较成功地解决了低维数据的聚类问题。但由于实际应用中存在数据的复杂性，特别是面对高维数据和大型数据的情况下，现有算法的性能则亟待改进。

随着技术的进步，数据收集越来越容易，导致数据库规模越来越大、复杂性越来越高，其维度（属性）通常可以达到成百上千维，甚至更高。因此，许多在低维数据空间表现良好的聚类方法往往在高维空间上无法获得好的效果（图1 为二维和三维空间下的聚类结果对比）。聚类效果的好坏主要取决于2 个因素：一是衡量距离的方法（distance measurement），二是聚类算法（algorithm）的选择。聚类分析的核心是选择合适的聚类算法，目前许多聚类算法在小于200 个数据对象的情况下成效明显，但对于一个大规模数据库，将导致结果有很大的偏差。因此，亟需研发出一个具有高度可伸缩性的聚类算法。迄今为止，高维聚类分析已成为一个重要研究方向，同时也是聚类技术的难点。

图1 二维、三维空间下的聚类Fig.1 Clustering in two-dimensional and three-dimensional spaces

1 k-means 算法

通过研究经典和常用的聚类方法，并分析比较各自的优缺点后可以发现：k-means 算法不仅容易理解，而且也容易用代码实现。k-means 算法采用基于划分的方法，简单易行、效率高，现已广泛应用于大规模数据的聚类分析中，目前绝大多数聚类分析的研究均围绕着该算法进行扩展和改进。

1.1 算法原理

k-means 中的是指簇的个数，需预先指定。迭代时选择簇内样本的均值向量作为簇的中心。k-means 聚类算法的核心思想是把若干数据对象划分为个聚类，使每个聚类中的数据点到该聚类中心的平方和最小。算法的主要步骤如下：

从若干数据对象中任意选择个对象作为初始聚类中心。

根据每个聚类对象的均值（中心对象），计算每个对象到这些中心对象的距离，并根据最小距离重新对相应对象进行划分。

计算每个（有变化）聚类的平均值（中心对象）。

循环Step2、Step3，直到每个聚类不再发生变化为止。

1.2 算法优缺点

k-means 算法的优势主要有：简单、易于理解和实现，只需要计算点和簇中心之间的距离即可，所以运算速度非常快；收敛快，一般仅需5～10 次迭代即可；高效，时间复杂度为（**）。

对于k-means 算法存在的问题，可做分述如下：

（1）必须设置簇的数量（预先给定值）。由于是先验给定的，但值却往往难于确定，特别是对于大型数据集，在算法启动前是无法精准给出的。

（2）k-means 算法对初始选取的聚类中心点是敏感的，需要研发出初始随机种子点启动算法，且随机种子点的选取至关重要。不同的随机种子点得到的聚类结果完全不同。一般从随机选择的聚类中心开始执行，可能会在算法的不同运行过程中，产生不同的聚类结果，这也会导致结果无法复现且缺乏一致性。

（3）对噪点过于敏感。因为算法是基于均值的，但均值求取上有时也并不简单。如：对于球形簇的分组效果较好，而对非球型簇，特别是不同尺寸、不同密度的簇分组效果却欠佳。如果初始点选择不当，最终的分组效果就会存在很大的差异，如图2 所示。

图2 初始点选择后的分组效果对比图Fig.2 Comparison chart of grouping effect of initial points selection

1.3 改进方法总述

针对k-means 算法存的问题，考虑到本文重点研究的学生成绩数据库的实际问题，在开展聚类分析过程中，本文将进行适当的优化，以减少算法缺陷导致的不良结果。

研究中，需选取合适的值，就要用到先验知识。常见的方法有拍脑袋法、肘部法则（Elbow Method）、间隔统计量（Gap Statistic）、轮廓系数（Silhouette Coefficient）、Canopy 算法等。比照这些方法，本文借鉴选用一种简单且操作简便、基于平方误差的计算方法来确定值。

针对值需事先给定的问题，在没有先验经验的情况下，可采取几种不同的值尝试，分别计算平方误差（值），找到“拐点”。基于平方误差的计算公式为：

其中，为簇内样本数，为簇的中心。值越小，说明簇内样本距离越小，相似度越高。

研究得到的平方误差曲线如图3 所示。由图3可知，当5 时，聚类性能基本达到最优效果；当继续增加时，性能并没有明显变化，则可将最终的聚类算法值选择为5。

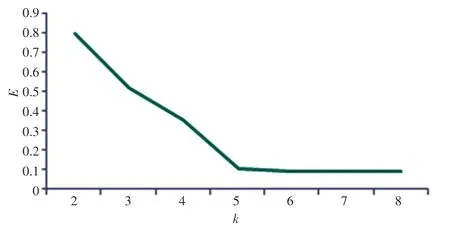
图3 平方误差曲线Fig.3 Square error curve

k-means 算法是初值敏感的，选择不同的初始值可能导致不同的簇划分规则。如k-means++算法就是针对K-means 聚类算法中随机选取初始聚类中心的缺陷问题的改进，这是一种基于数据分布选取初始聚类中心的算法，整体上与k-means 算法相差不大，同样是采取迭代更新的思想。算法的主要改进是在第一步选取个初始聚类中心时，不再是在整个数据集中随机选取个数据对象作为初始聚类中心，而是遵循初始的聚类中心之间的距离应尽可能远的原则，选取个初始聚类中心。

借鉴k-means++算法的一些思想，本文对于初始值的选取采用简化的办法。在选择初始点时，可以选择距离尽可能远的点；在预处理阶段，对数据进行归一化处理时，可考虑剔除噪点。如果99%的学生成绩在20～95 之间，只有1%的学生成绩超过95或是低于20，则在做归一化处理时，可选取99%学生中成绩的最高分作为最大值，剩余1%的学生成绩直接置为1 即可。

2 实验结果验证与分析

现行的以考试成绩绝对分数来衡量学生学习状况的方法比较主观，且评价方式过于单一。例如：成绩在90 分以上为优秀，成绩在60 分以上为及格，低于60 分为不及格等。这样的处理方法虽简便易行，但存在一些不妥之处，如成绩中有用信息未获重视、成绩绝对分值相差不大但划分后相差很大、总体成绩的动态分布情况不合理等现象出现，导致无法公正、合理、有效地评价学生成绩。充分挖掘、且利用隐含在学生成绩中的有用信息，并采取针对性的措施，如能从学生期中考试成绩挖掘出一些预判性的有用信息，并采取积极有效措施，就有可能提高学生的期末考试成绩。为此，通过上述聚类方法尝试进行相关成绩分析很有必要。

为了实现系统的可视化，采用Java 与PHP 混合编程，借鉴经典的k-means 聚类算法，优化和改进初始点及值的确定，并同时最大限度地保证系统的稳定性。主要数据源来自北京超星学习通平台中具体课程相关班级的部分科目期中考试成绩，导出数据为Excel 表格形式，成绩均为百分制。前期进行数据清洗，主要去除一些无关或空白数据，如学生缺考将会置零并删除，以免影响聚类结果。

2.1 聚类分析

基于聚类分析的成绩划分是将原有绝对成绩划分改为相对成绩的划分。每个簇组成一个成绩群，每个簇中心的数据就是该成绩群的中心成绩。这些中心成绩是学生成绩等级划分的参考标准之一，因此用于学生成绩评价也更为准确。通过聚类分析，将学生成绩划归到各个簇中，簇的大小、形状、中心值可以用来评价教学效果的好坏。

通常，聚类个数值要尽可能地接近所用的聚类变量的个数。如：5 个变量用于聚类分析，通常就会分为5 个类。类个数太多不利于对类的解释；太少不利于分开，并降低了类的同质性。比较可行的办法是每次用不同类的个数来做实验并对比所得结果，确定最理想的类个数。通过k-means算法聚类划分学生成绩数据，类的个数从1 到8，依次运行一遍，计算类内平方误差和J（1，2，3，…，8），绘出J和值个数的曲线图。在J值随变化的曲线上，其拐点对应的类别数基本接近于最优聚类个数。文中绘制得到的值选取曲线如图4 所示。由图4 可见，J随的增加而单调减少。当值为68 时，J呈平缓状态，因此可以认为6 是比较合适的聚类个数。

图4 k 值选取曲线图Fig.4 k value selection curve

2.2 聚类结果评价

从学生成绩数据库中随机选择6 个学生的学习成绩作为初始聚类中心，经过k-means 聚类算法生成6 个类别，见表1。

表1 生成的最终聚类中心Tab.1 Generated final cluster centers

在学生成绩评价中通过聚类分析发现，每一个类就是一个成绩群，处于每个类中心的数据就是该成绩群的中心成绩。例如：第4 类学生的计算机基础成绩随中心值82.51 的变化与第6 类学生的大学英语成绩随中心值74.23 的变化如图5 所示。由图5 可以看出相近的成绩都被划分到了同一类，避免了采用传统划分方法可能出现“学生成绩差别不大，划分后结果可能相差很大”的情况。另外，每一科成绩随中心的变化就是相对于整体成绩的分布情况。

图5 学生成绩随聚类中心变化图Fig.5 Changes in student grades with cluster centers

总之，该聚类分析不仅可以使学生清楚自己相对于整体成绩的位置，还可以体现某类学生在某些学科的不足，从而提醒任课教师采取针对性措施。从表1 中所划分的类的人数及中心成绩可以看出，所有学生前三门基础学科成绩较低，尤其大学英语成绩最低，而思政课程的成绩就相对较高。同时也可以看出，每一类学生哪些学科成绩相对偏低，从而制定有效改进的解决办法，提高学生期末考试的成绩。比如第二类别英语成绩最低的这一部分学生，可以反映给学校教务处适当增加英语学科的课时，具体评价解释见表2。

表2 聚类评价和解释Tab.2 Cluster evaluation and interpretation

3 结束语

随着人工智能技术在各类信息化领域中的不断深入，学习过程中数据源的大量涌现，作为常见的无监督学习的典型算法—k-means 聚类算法，对其在个性化学习系统中开展相关应用研究有着广阔的前景。本文从经典的k-means 算法出发，探索并寻找一种效率更高、稳定性更好的聚类分析方法，并在个性化学习系统中进行实践，取得了不错的应用效果，也为后续的进一步研究提供了有益借鉴。