季冻区玄武岩纤维复合高粘改性沥青性能评价

于保阳， 刘美鸥， 孙宗光

(1. 大连海事大学 交通运输工程学院， 辽宁 大连 116026； 2. 沈阳建筑大学 交通工程学院， 沈阳 110168； 3. 中铁九局集团 第一建设有限公司， 江苏 苏州 215299)

1 试验设计与指标分析

1.1 试验原材料

本文采用玄武岩纤维、高粘改性剂与辽河90#基质沥青进行复合改性沥青试验.表1为基质沥青技术指标.玄武岩纤维由海宁安捷有限公司生产，其基本技术指标如表2所示.高粘改性剂为国产OLB-1型，由多种聚合物复合而成，如图1所示.

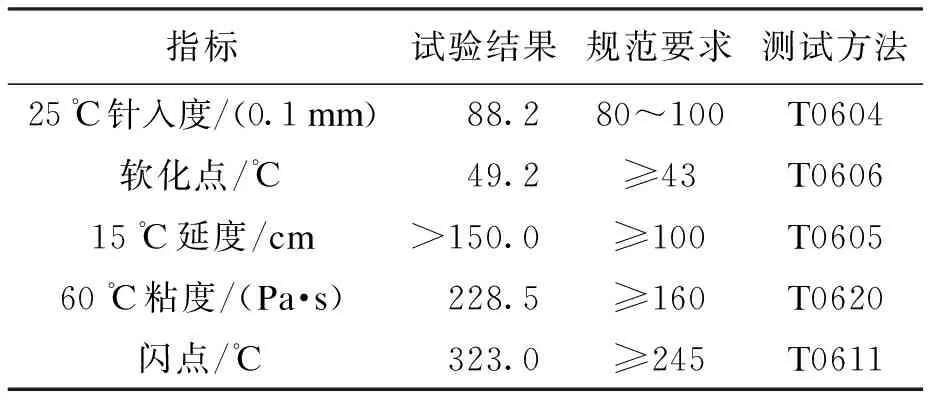
表1 基质沥青技术指标Tab.1 Technical indexes of matrix asphalt

表2 玄武岩纤维技术指标Tab.2 Technical indexes of basalt fiber

图1 高粘改性剂Fig.1 High viscosity modifier

选取高粘改性剂掺量、玄武岩纤维掺量共2个影响因素，参考透水沥青路面工程中的高粘改性剂掺量为8%和玄武岩纤维掺量为3%(占沥青胶浆的质量百分数)两种试样[11-12].每个因素取4个水平，采用正交试验方法对复合改性沥青进行试验设计.其中，基质沥青中的玄武岩纤维掺量为0%、1%、3%、5%；高粘改性剂掺量为0%、4%、8%、12%，试验试样共16组.对两种改性材料不同掺配比下复合改性沥青的软化点、延度、锥入度、135 ℃粘度和小梁弯曲蠕变(BBR)指标进行试验.

1.2 试验结果与分析

1.2.1 粘度指标

针入度、软化点、135 ℃粘度均为沥青粘度的一种表征形式.由于玄武岩纤维与高粘改性剂加入基质沥青中形成了非匀质状态的复合改性沥青，若用针入度法测量复合改性沥青的粘稠性，离散程度较大并且试验结果不稳定，因此本文采用锥入度法进行测试[13].不同掺配比下复合改性沥青的粘度指标测试结果如表3所示.

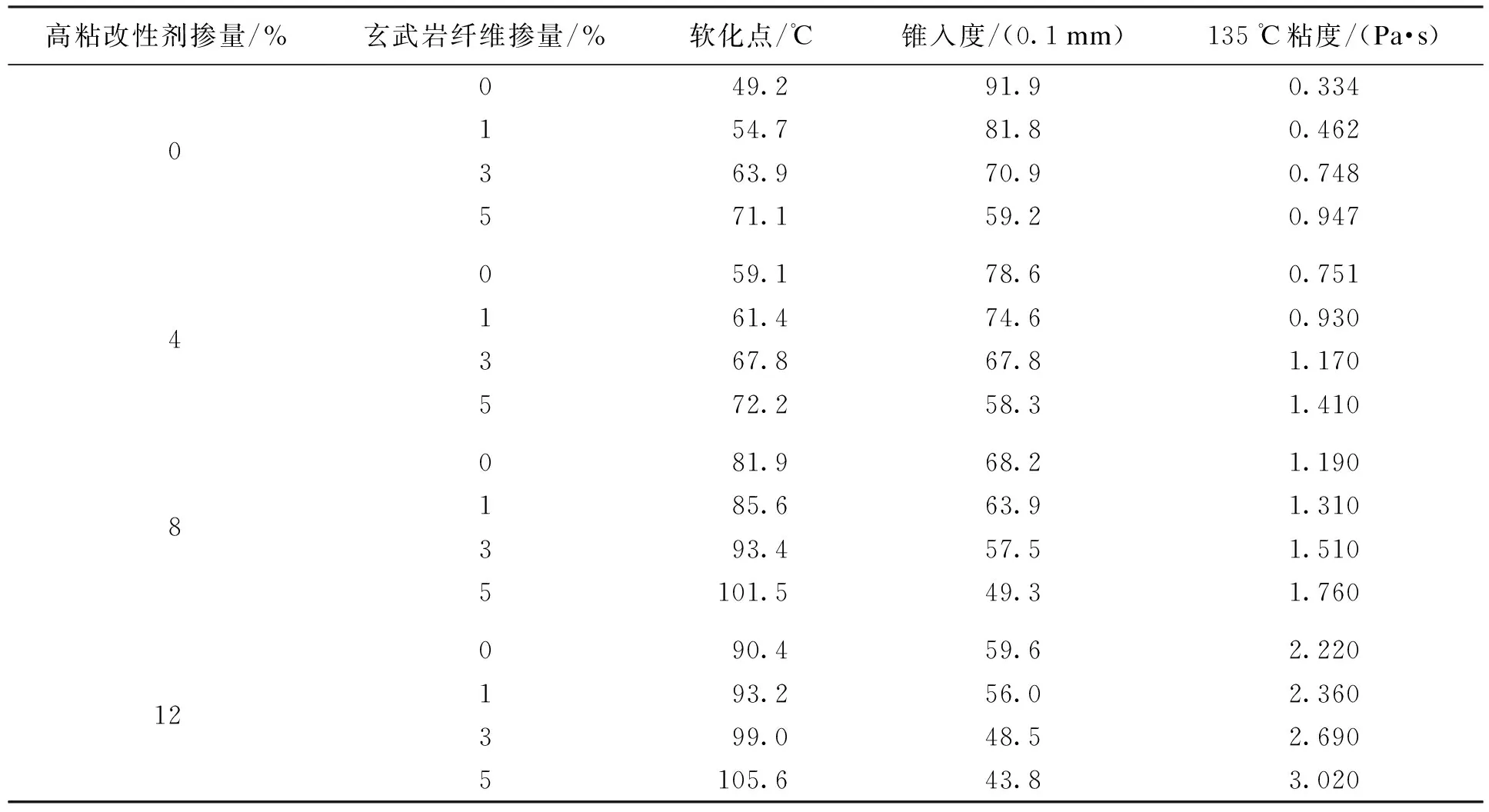
表3 复合改性沥青粘度指标及试验结果Tab.3 Viscosity index and test results of composite modified asphalt

通过表3数据分析可知，单一使用玄武岩纤维或高粘改性剂加入沥青后，会对沥青的粘度指标产生影响.而对于两种材料共同使用时，随着掺量的增加，复合改性沥青的软化点、135 ℃粘度明显增大，锥入度下降.本文对玄武岩纤维和高粘改性剂不同掺配比与粘度指标建立线性方程，对复合改性沥青进行粘度预测分析.

1.2.2 延 度

延度指标能够间接评价沥青的低温性能，延度越大，低温延展性越好，低温条件下变形程度越高，抵抗开裂性能越好.本文选择5 ℃环境条件对16组改性沥青进行低温延度试验.图2为复合改性沥青延度试验结果.

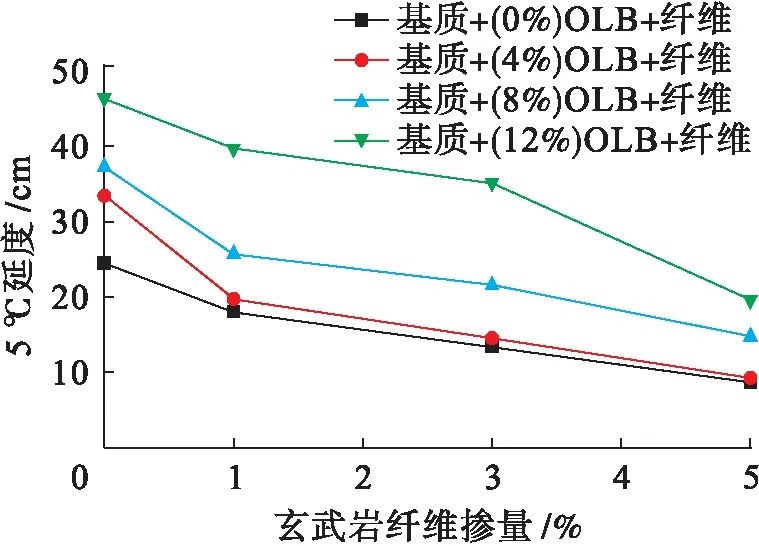
图2 复合改性沥青延度试验结果Fig.2 Ductility test results of composite modified asphalt

由图2可知，不掺加玄武岩纤维时，随着高粘改性剂掺量的增加，延度值增大；当高粘改性剂掺量为0%、4%、8%、12%时，随着玄武岩纤维掺量的增加，延度值减小.玄武岩纤维吸收沥青内的轻质组分，使得沥青体现出脆性，掺量增大使其延展性降低；高粘改性剂的掺入能够增强纤维与沥青间的粘结作用，提高沥青在低温时的拉伸变形能力，弥补纤维掺入后延度降低的不足，体现出两种材料复合改性的优势.

1.2.3 低温蠕变试验

为了进一步研究复合改性沥青低温性能，本文引入低温蠕变试验，试验采用低温弯曲流变仪(BBR).在不同温度下，对16组不同掺配比复合改性沥青浇筑的小梁试件进行测定，得到其劲度模量S和蠕变速率值m.

SHARP计划提出，沥青的劲度模量S值过大，沥青呈现脆性，表示模量值越小越好，沥青抵抗永久变形的能力越强；沥青的蠕变速率值m越大，表明沥青劲度的时间敏感性越强，路面随着温度降低发生收缩时产生低温开裂的可能性减小[14-16].本文根据东北气候条件，采用BBR分别在-18 ℃和-24 ℃条件下对复合改性沥青进行低温弯曲蠕变试验，进一步评价其低温性能.表4为东北季冻区气候条件数据.图3～4为两种温度下复合改性沥青蠕变劲度模量值和蠕变速率值.

表4 东北季冻区气候条件Tab.4 Climate conditions of seasonal frozen region in northeast China

图3 复合改性沥青蠕变劲度模量值Fig.3 Creep stiffness modulus of composite modified asphalt

由图3可以看出，在-18 ℃和-24 ℃，S值随着温度的下降而升高，温度降低，沥青的低温变形能力变差.在掺入两种改性材料后，沥青的蠕变劲度模量S值呈现减小的趋势.当高粘改性剂的掺量一定时，S值随着玄武岩纤维掺量的增加先减小后变大；当玄武岩纤维掺量一定时，S值随着高粘改性剂掺量的升高先增大后减小.在两种温度下，玄武岩纤维与高粘改性剂掺配比为3%和12%时的S值均达到最小，说明两种材料可以综合提高沥青低温变形的能力.但当纤维掺量大于3%时，S值开始变大，这是因为过量的纤维在高温浇筑试件时极易粘结成块状，导致低温下沥青的蠕变模量增大.

由图4可以看出，在不同温度下，温度越低，沥青的蠕变速率值m越小.当掺入玄武岩纤维和高粘改性剂后，m值先增大后减小，玄武岩纤维掺量为1%时达到最大，该掺量下玄武岩纤维与高粘改性剂复合改性对于提高沥青的应力松弛能力最佳.随着两种材料掺量的增大，复合改性沥青应力松弛能力下降.在-24 ℃条件下，玄武岩纤维掺量为5%时，不同高粘改性剂掺量下的m值呈接近趋势，如果继续增加纤维掺量，各掺配比下的复合改性沥青的应力松弛能力将达到限值不变.虽然两种材料可以综合提高沥青的低温抗永久变形和应力松弛能力，但要在合理掺量的范围内使用.

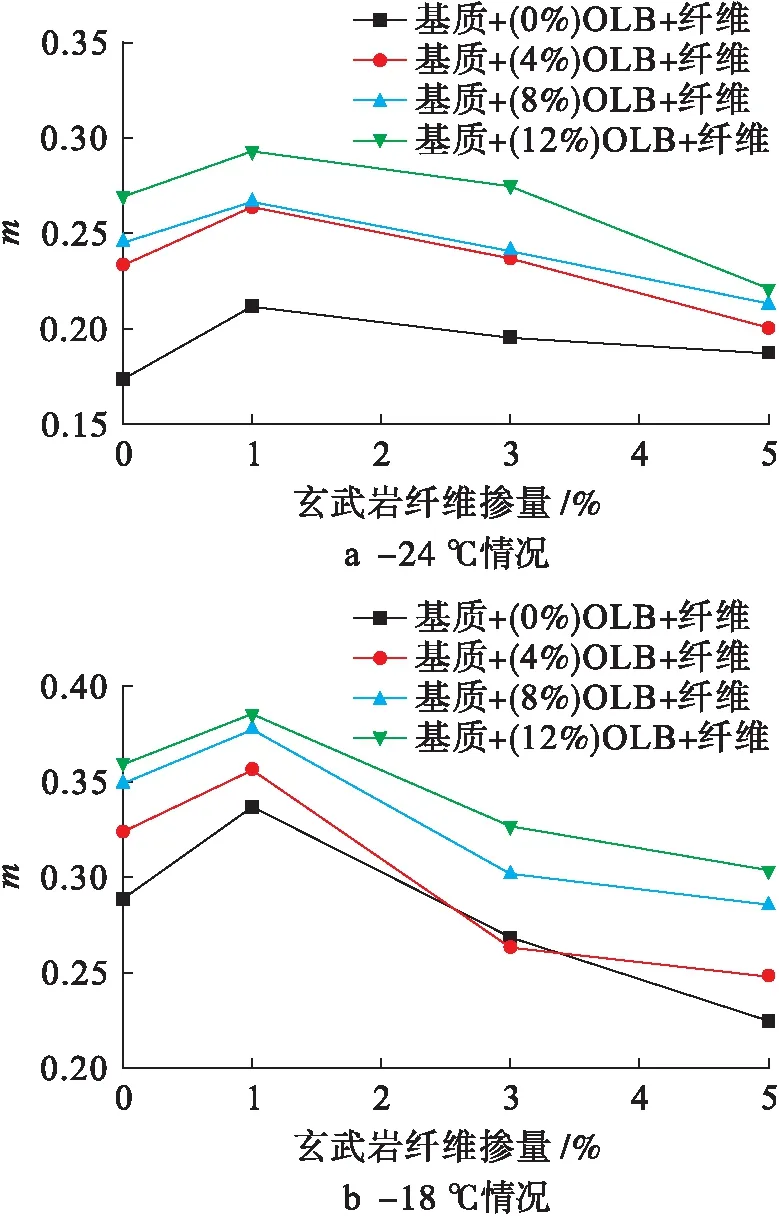
图4 复合改性沥青蠕变速率值Fig.4 Creep rate of composite modified asphalt

2 复合改性沥青增粘预测

本文将玄武岩纤维与高粘改性剂同时作为固态的增强剂掺入基质沥青中，以物理混合方式影响沥青的性能.以复合材料理论的广义混合率为依据，将复合材料的性能看作是各组分的性能与相应体积含量乘积的加权和，其表达式为

(1)

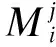
在高温条件下，复合改性沥青是以沥青为液体，玄武岩纤维和高粘改性剂为固体的复合体系，对于两相复合的固液悬浮体系来说，复合材料的广义混合率公式可以表示为

M=MW(1-VS)1/j

(2)

式中：M为复合改性沥青的粘度指标(软化点、锥入度、135 ℃粘度)；MW为基质沥青粘度指标值；VS为固体颗粒的体积分数.

当式(2)满足Albert Einstein在其经典论文《论分子大小的测定》中做出的若干假设之后，即可推导出爱因斯坦增强模型(粘度方程式)为

M=MW(1+KEVS)

(3)

式中，KE为爱因斯坦系数.KE也可看作改性材料的增粘速率，随着沥青中逐渐加入两种改性材料的掺量变化，两种改性材料产生一定的交互作用使增粘速率产生变化.根据爱因斯坦假设，两种改性材料的固体粒子等大，在爱因斯坦粘度公式中加入交互作用系数β，拟定出复合改性沥青粘度公式为

M=MW(1+βKEMh)=

MW[1+βKE(Mx+Mg)]

(4)

式中：Mh为玄武岩纤维与高粘改性剂的总质量分数；Mx为玄武岩纤维质量分数；Mg为高粘改性剂质量分数.总质量分数为两种改性材料的质量分数之和.

2.1 增粘方程拟合

根据表3中数据，当高粘改性剂掺量一定时，利用式(3)对不同玄武岩纤维掺量下的复合改性沥青的粘度指标进行拟合，拟合结果如表5所示.

表5 不同高粘改性剂掺量的玄武岩纤维增粘方程Tab.5 Viscosifying equation of basalt fiber at different blending contents of high viscosity modifier

2.2 交互作用系数

将高粘改性剂掺量为4%、8%、12%时的复合改性沥青增粘速率与高粘改性剂掺量为0%时的纤维改性沥青增粘速率的比值作为交互作用系数βn′(n′=1，2，3)，并对所得交互作用系数进行方程拟合，结果如表6～7所示.

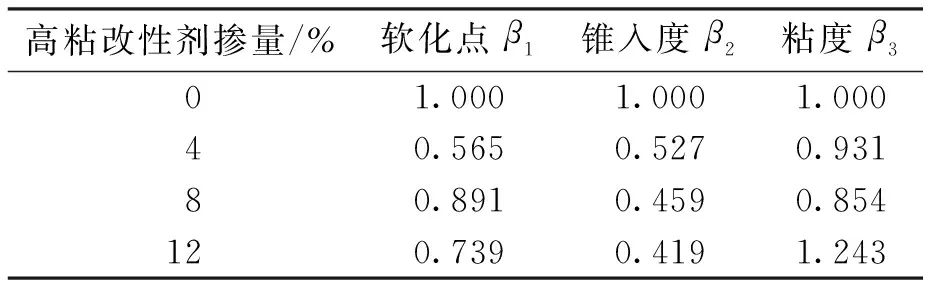
表6 不同高粘改性剂掺量的交互作用系数Tab.6 Interaction coefficient of high viscosity modifier at different blending contents

2.3 增粘预测模型

将表7中交互作用系数方程代入式(4)中，可得到复合改性沥青的粘度指标(软化点、锥入度、135 ℃粘度)的预测模型.

表7 不同高粘改性剂掺量的交互作用系数方程Tab.7 Interaction coefficient equation of high viscosity modifier at different blending contents

软化点预测模型为

LSP=49.2[1+0.092(1-0.307 13Mg+

锥入度预测模型为

135 ℃粘度预测模型为

LV=0.334[1+0.379(1+0.023 25Mg-

3 复合改性沥青性能的综合评价

3.1 熵值组合权评价法

本文对16组玄武岩纤维与高粘改性剂不同掺配方案下的复合改性剂沥青建立软化点、锥入度、135 ℃粘度、延度、低温蠕变多指标体系，同时考虑复合改性沥青对东北季冻区透水路面的适用性，需要对沥青的高低温指标进行主观赋权来确定主观权重系数，熵值法确定客观权重系数，最后将主客观权重系数“加成”得出各掺配方案的综合评分.计算步骤如下：

1) 数据矩阵.将表1、图2～4中试验数据代入矩阵A中，方案序号和指标顺序(从左至右为1，2，…，8)如表8所示.

式中，Xij为第i个方案第j个指标的数值，i=1，2，…，n，j=1，2，…，q.

2) 数据的非负数化处理.为了避免求熵值时对数的无意义，需要进行数据平移.

① 对于越大越好的指标，则有

(5)

② 对于越小越好的指标，则有

(6)

为了方便起见，记非负数化处理后的数据为Xij.

3) 计算第j项指标下第i个方案占该指标的比重为

(7)

4) 计算第j项指标的熵值为

(8)

5) 求组合权值.

① 熵权值为

(9)

② 主观赋权.本文参考大量研究资料确定复合改性沥青性能指标的模糊权向量[17-18]，并考虑季冻区最低温条件下沥青性能指标的适用性，对其多性能指标进行主观权重分配，即

λ=(λ1，λ2，…，λn)=

(0.1，0.1，0.1，0.1，0.15，0.15，0.15，0.15)

③ 组合权值为

(10)

6) 计算各方案的综合评分为

(11)

3.2 数据分析

将矩阵A按式(5)～(11)计算，得到16组复合改性沥青指标试验数据的非负数化处理值、熵权值、组合权值及各掺配方案的综合评分，计算结果如表8所示.

由表8计算结果分析可知，方案15得到最高的综合评分为3.22，为最佳掺配方案，与试验结果分析相互验证，在方案15掺配比下复合改性沥青的低温变形能力最强，两种改性材料的最佳掺配比为高粘改性剂掺量12%，玄武岩纤维掺量3%.

表8 复合改性沥青性能的熵值组合权综合评分Tab.8 Comprehensive scores of composite modified asphalt performances with entropy-combination weight

4 结 论

本文通过分析得出以下结论：

1) 通过多指标沥青性能试验，确定复合改性沥青的最佳掺配比，高粘改性剂掺量为12%，玄武岩纤维掺量为3%.

2) 建立复合改性沥青的增粘预测模型，拟合复合改性沥青的增粘方程，可以较为精准地预测复合改性沥青在不同掺配比下的性能.