高气压氩气辉光放电条纹等离子体的形成和演化*

朱海龙 师玉军 王嘉伟 张志凌 高一宁 张丰博

(山西大学物理电子工程学院,太原 030006)

辉光放电等离子体正柱区内的自组织条纹现象是气体放电物理中的基础性问题,涉及电子动力学、输运过程、放电不稳定性、非线性现象等丰富的物理内容,是基础物理及其应用中备受关注的重要课题.本文报道了一种在千帕量级气压下产生的氩气辉光放电条纹等离子体,重点关注了条纹等离子体的电学、光学及电离波传播特征,从物理上分析了氩气条纹等离子体的产生及消除机制.研究结果表明,在此气压下产生的氩气条纹等离子体,其条纹长度约为1.5 mm,且随气压减小;电离波波速为1.87 m/s,频率为1.25 kHz.发射光谱诊断证实,条纹等离子体的产生与丰富的亚稳态原子密切相关,亚稳态原子导致的分步电离过程会引起电离不稳定性,这种不稳定性以电离波的形式传播,使得等离子体参数发生纵向调幅,从而形成明暗相间的条纹等离子体.加入氮气可有效猝灭亚稳态氩原子,调整电子能量分布函数,这使得等离子体的不稳定性条件被破坏,因此,条纹等离子体消失.本工作可为人们进一步认识和理解高气压下辉光放电条纹等离子体的形成及消除机制提供新的思路和实验依据.

1 引言

众所周知,辉光放电等离子体是一种典型的碰撞等离子体,其中包涵了丰富的高能电子、离子、激发态粒子等,放电过程中存在着复杂的集体作用和非线性现象;它在现代科学技术,如气体激光器[1,2]、微电子工业[3,4]等领域中有重要且广泛的应用,是近年来基础研究中备受关注的研究热点.

辉光放电等离子体的正柱区常会呈现不连续的、明暗相间的条纹结构,因此被称为辉纹(图1).辉纹是一种典型的放电非线性现象,也是一种特殊的辉光放电,具有区别于正常辉光放电的物理机制.辉纹按是否发生移动分为固定辉纹和移动辉纹.固定辉纹是指其产生后不会在放电电极间传递的条纹,一般发生在氢气、氮气、空气等双原子气体放电环境中或者由分子气体和稀有气体所组成的混合气体放电中,它能被肉眼清晰分辨;移动辉纹一般存在于惰性气体中,其移动速度可以达到10—1000 m/s,不易被肉眼所分辨,但有时移动辉纹会同固定辉纹共存[5].辉纹被认为是由不稳定性引起的电离波,由放电时的输运过程、电离过程和电子动力学行为所支配,明纹是电子碰撞电离和激发频繁的区域,而暗纹中电离过程较弱,扩散过程和电子损失占主导地位[6,7].

图1 几种典型的辉纹 (a) 250 Pa 下的氩气辉纹[8];(b) 133 Pa下的氮气 辉纹[9];(c) 18 kPa 下的氦气辉纹;(d) 38 kPa 下的氩气辉纹Fig.1.Several typical striations:(a) Argon striation at 250 Pa;(b) nitrogen striation at 133 Pa;(c) helium striation at 18 kPa;(d) argon striation at 38 kPa.

辉纹的形成对气压十分敏感,一般在低气压下(Pa 量级)容易被观察到,近年,在中等气压、大气压甚至更高的气压下也观察到了辉纹.条纹的长度与气压的依赖关系服从Goldstein-Wehner 定律[10]:λ/R=C/(pR)m,其中λ 为条纹长度,R是放电管半径,C和m都是常数,它与气体类型有关[11].此外,辉纹的形成还与放电电流和气体成分密切相关.在确定的气压下,放电电流增大到某一临界值时条纹就会消失,这一临界值被称为Pupp 界,可表示为I=A/(pR)n,A和n常数[12].辉纹间电势降满足Novák定律[13],Uλ=E·λ,E是周期性电场.例如,对于氖气辉纹,在放电条件为0.4 ＜pR＜ 5 Torr·cm (1 Torr=1.33×102Pa),I/R≤ 0.1 A/cm,可形成3 种类型的辉纹,分别命名为p 型、r 型和s 型辉纹,它们的Novak 势降分别为9.8,13.5 和 20 eV[6];对于氩气辉纹,它们的值分别为5.8,7.7 以及11.55 eV[14].

目前,对辉纹产生机制的认识还有不足,物理图像还不够清晰,这是由于辉纹类型的多样性、辉纹属性对放电条件的复杂依赖性,以及电子动力学数据的缺乏,使得合理解释各种条纹的形成过程成为一个异常困难的问题.起初人们利用各种类型的波动机制解释辉纹的形成机制,例如,离子声波,驻波等,后来研究发现辉纹是非平衡气体放电等离子体的固有现象,等离子体中的电离、激发过程,输运过程及电子动力学过程在辉纹的形成过程中起主导作用[6,15].

大部分辉纹是在低气压下产生的,电子动力学共振是低气压下辉纹形成的重要机制[16,17].电子从阴极出发,在电场的作用下加速,当电子的动能ε 达到或大于原子的激发能阈值εe时,电子就会与原子发生非弹性碰撞变为慢电子,其损失的能量为εe,这些慢电子继续被加速,继续发生非弹性碰撞,如此反复下去就会形成周期性的电子能量分布函数(EEDF)[18]、电子密度及电场分布,在电极间隙形成了明暗相间的条纹放电.然而,在高气压下(大于100 Torr)[19],由于电子的平均自由程减小,电离、激发及复合过程异常频繁,电子动力学共振行为成为了非主导因素.例如,在低气压下粒子的损失机制是扩散以及表面复合,而高气压下体积复合就变得重要,电离和激发过程也需要考虑分步电离和分步激发.此外,高气压下,电流的增大会使得放电由扩散模式向收缩模式转变,此时,等离子体的某些参量在较小的扰动下会失去稳定性,表现为电离率和电子密度呈现非线性效应[20].因此,高气压下,辉纹的形成机制常常认为是由放电不稳定性引起.Golubovskii 等[21,22]通过数值模拟和实验证实,高气压下,辉纹的形成常伴随着放电通道的收缩,这在氩气放电中十分明显;并且认为非均匀气体加热、分步电离以及电子能量分布函数背离麦克斯韦分布会引起不稳定性,这种不稳定性的发展和传播引发了放电通道的径向收缩和纵向分层.具体到惰性气体放电,如氦气或氩气,放电过程中会产生大量的亚稳态原子,这些亚稳态原子具有较长的寿命(He[23S]:7870 s[23],Ar [1 s5]:5.5±0.5 ms[24])和极高的能量阈值 (He[23S]:19.82 eV,Ar [1s5]:11.55 eV)[5],这使得它极易与慢电子发生碰撞发生电离,称为分步电离.当分步电离与电子直接碰撞电离相当时,甚至分步电离主导整个电离过程时就会引起电离不稳定性.Siefert 等[25]通过数值模拟证实,若考虑亚稳态原子导致的分步电离过程,就会导致电子密度的波动,电离率和电子密度发生一定相移,电离不稳定性就会以波的形式向前传播,形成辉纹.

近年,在大气压[26]甚至更高的气压下[7],各种激励源(直流[27]、射频[14,28]以及微波[29])驱动的放电等离子体中都发现了辉纹现象,笔者课题组在千帕量级气压下,直流脉冲驱动氦气等离子体中也发现了辉光放电条纹,并且研究了氦气辉纹的电学、光学和电离波特性[30].本文在前期工作的基础上进行了拓展,对比性地研究了氩气辉纹的放电特征,重点关注了与亚稳态原子有关的4 条发射线的变化规律,分析了由亚稳态原子引发的分步电离过程,及其对电离不稳定性的影响,揭示了注入氮气后辉纹消失的原因.

2 实验装置与方法

辉纹等离子体产生装置见图2,其中包括真空腔体,电极调节装置,气体控制端,以及电源激励装置.真空腔体容积为295 mm × 150 mm × 149 mm,腔室内置两个铜制电极,电极结构为针-针式,针长为5 cm,直径为8 mm,针尖直径约为50 µm,针尖的斜面角度30°,两电极与不锈钢导轨机构相连,用于可控调节电极间距和等离子体形态.腔体左端置有抽气阀和充气阀,抽气阀和旋片式真空泵相连,用以控制所述腔体内气压,右端置有一真空测量规在线监测腔体内部的真空度.实验所用电源是一台直流脉冲高压电源.辉纹的产生过程如下,首先建立适宜自组织条纹等离子体生成的气压环境,约7.00 kPa,并保持此气压值不变;其次调节导轨机构使电极间距保持在3 mm,开启高压电源在电极两端施加电压击穿气体形成正常辉光放电等离子体;开启充气阀向腔室内缓慢通入氩气至气压区间21.22 kPa,与此同时调节导轨机构使得电极间距保持10 mm,在正负电极的间就会形成明暗相间的条纹状等离子体.实验过程中采用高压电压探头 (Agilent 10076 B,100:1) 与示波器 (Tektronix TDS2014) 相连,用于测量放电过程中的电压信号;放电回路中接入一个 100 Ω 的取样电阻用于测量放电电流;光谱测量系统由凸透镜(焦距为12 cm),成像屏(其中的狭缝为0.5 mm),光纤光谱仪(Avaspec ULS2048 USB2) 和计算机构成,如图2 所示,将放电发光等大成像到真空室外的成像屏上,光穿过狭缝进入光纤探头,测量到的等离子体发射光谱在计算机上显示并记录;放电图像由一台数码相机(Canon EOS760 D) 记录.此外,对放电图像进行了后处理,以获得更直观、更精确的放电形态.数码相机得到的辉纹图像是彩色RGB 图像,它是由偶R(红色)分量、G(绿色)分量和B(蓝色)分量3 个基色分量叠加而形成的.基于此,利用MATLAB程序包并自行编制程序对放电图像进行灰度化和滤波降噪处理,进而对放电图像进行边缘提取,从而获得辉纹的边缘和条纹间距;通过计算放电图像轴向上每个像素的灰度值(0—255)分布,间接反映辉纹的光强分布.

图2 实验装置示意图Fig.2.Schematic diagram of the experimental setup.

3 结果与讨论

3.1 氩气辉纹放电图像特征

图3(a)所示为典型的高气压下 (21.22 kPa)氩气辉纹的放电图像,其特征是放电通道呈现不连续的,明暗相间的条纹状等离子体柱(从阴极端始,依次定义为1 级明纹,2 级明纹,3 级明纹…).由图3(b)所示的边缘检测图像可看到,每一级条纹厚度约为1.5 mm (明纹约为1.0 mm,暗纹约为0.5 mm).从阴极至阳极,辉纹的灰度值(间接反映发光强度)也呈现周期性分布 (图3(c)),柱区的发光强度较弱于阴极端(阴极辉区)和阳极端(阳极辉区),每级明纹存在一个带头 (近阴极端),且具有较高的发光强度.与我们在类似的条件下获得的氦气辉纹相比[30],氩气辉纹的条纹间距更短,且没有明显的法拉第暗区,这是由于氩气具有较低的第一激发能 (氩:11.55 eV,氦:19.82 eV),电子被加速到第一激发能所经历的路程更短.此外,氩气和氦气放电通道形态存在一定的差异性,氩气辉纹较易呈现弧形的收缩通道,气压越大,弧形越大;而氦气放电通道相对弥散,是直线形或弱弧形.研究表明,放电通道收缩主要是由于电离率对电子密度的非线性关系,以及复合导致的带电粒子的损失[31],氦气放电比氩气放电较弥散,收缩效应较弱,这与氦气比氩气具有较低的原子质量和较高的热导率有关[32].

图3 (a) 氩气辉纹放电图像,电极间距为10 mm,气压为21.22 kPa,曝光时间为1/200 s;(b) 辉纹边缘检测图像;(c) 辉纹灰度值分布Fig.3.(a) Typical image of argon striation plasmas in electrode spacing of 10 mm and gas pressure of 21.22 kPa,within exposure time of 1/200 s;(b) image edge detection of striation;(c) gray distribution of striation plasmas.

3.2 氩气辉纹电学、光谱学特征及产生机制

图4 给出了典型的放电电压和电流特征波形.放电电压和电流峰值分别为414 V 和3.9 mA,每个电压周期进行一次放电,放电电压和放电电流具有相同的频率,约为40 kHz.图5 所示为明纹(2 级明纹) 的特征发射光谱图.放电过程中,检测到20 条氩的发射线 (主要是Ar I),对应的激发能处于13—15.5 eV;并未检测到Ar II 发射线,这是由于Ar II 线对应更高的激发能19—22 eV.这表明放电过程中电子能量分布函数的“尾巴”主要分布在13—15.5 eV 这一区间.图6 给出实验中检测到所有Ar I 线对应的能级和跃迁图.所有谱线主要来源于激发态氩原子从能级3p54p (2p1—2p10) 到3p54s (1s2—1s5)的自发辐射跃迁,其中,3p54s 包含两个共振态(1s2和 1s4),两个亚稳态(1s3和 1s5).在惰性气体放电等离子体中,亚稳态原子的作用是非常重要的,这与它们的长寿命,高激发能,可存储能量等特点有关.在氩气辉光放电中,亚稳态原子的产生一方面来自于基态原子的碰撞激发,另一方面是来自于高激发态(如2p1—2p10) 的退激发过程,而且1s5态的密度要高于1s3态约2—5 倍[33].从图5 可以看到,发射强度较高的谱线分别是696.543 nm,763.511 nm,811.531 nm 和706.722 nm,且这4 条谱线全部来自于激发态氩原子从2p 态到1 s5亚稳态的退激发过程,它们分别为2p2—1s5,2p6—1s5,2p9—1s5以及2p3—1s5.这从一方面反映了明纹中包含了一定量的亚稳态氩原子,特别是1s5态原子.明纹与暗纹的光谱发射强度有显著的差别.图7 给出了这4 条谱线在各级明纹和暗纹处的强度变化规律.从1 级到5 级条纹,每一级条纹其明纹的谱线强度远高于暗纹,且谱线强度呈周期性变化,这与图3 所示的放光强度变化规律几乎是一致的.已知谱线强度与激发率有关,明纹处谱线强度高,意味着明纹处的激发率,激发态(包括亚稳态)浓度,以及平均电子能量要高于暗纹.

图4 放电电压和电流波形Fig.4.Typical waveforms of discharge voltage and discharge current.

图5 2 级明纹的发射光谱Fig.5.Optical emission spectroscopy of 2nd bright striation.

图6 氩激发态能级图Fig.6.Energy-level diagram for argon excited states.

图7 各级明暗条纹的发射强度Fig.7.Emission intensity of bright and dark striations.

亚稳态氩原子极容易与电子发生碰撞被电离,因为亚稳态氩原子具有较低的电离能量阈值,例如,对于1s5态其电离能为4.2 eV,而电子直接碰撞基态氩原子的电离能为15.76 eV.由于明纹存在大量的亚稳态原子,亚稳态原子被电子碰撞电离甚至主导了整个电离过程.这一过程被称为分步电离[6],可表达如下:

亚稳态原子的分步电离会引起电离不稳定性[34,35],其表现为电离率与电子密度会呈现一种非线性关系.这种不稳定的发展会引起等离子体参数的纵向调制,从而形成明暗相间的放电条纹.一旦亚稳态原子被部分猝灭,由亚稳态原子导致的分步电离就会被削弱,电离不稳定性就会减小,此时放电就会变得稳定.下文借助扰动理论来分析这种不稳定性.假设放电过程中存在一个小的电子密度扰动,这样电子密度ne就可以表达如下:

其中,ne(r)是稳态时的电子密度,是扰动下的电子密度,k决定扰动的纵向尺度或波长λ=2π/k.将方程 (3) 代入粒子平衡方程 (4):

其中Da是双极性扩散系数.代入后的电子密度扰动方程为

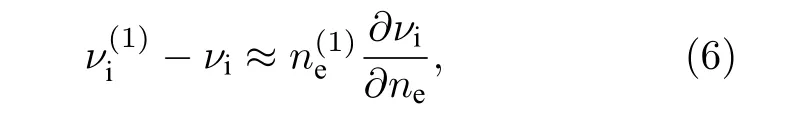
将(6)式代入(5)式得到扰动方程:

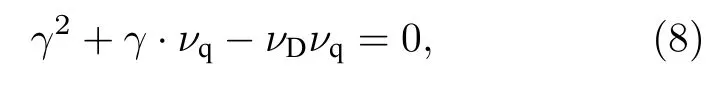
方程 (8) 中,νq是亚稳态猝灭率.方程 (8) 中总存在一个正的实数根,这表明放电过程中如果考虑亚稳态导致的分步电离过程,扰动必然随时间增长,从而引起电离不稳定性.电离不稳定性的发展会引起等离子体参数的纵向调幅,并以电离波形式传播,结果在等离子体柱中形成分层现象.当亚稳态猝灭率 (通过双原子分子N2或O2猝灭) 大于亚稳态激发率,这一模型就不会成立,因为此时电离过程会由分步电离主导转变成电子直接碰撞电离主导,放电变得稳定.3.4 节将分析放电过程中通入N2导致等离子体辉纹消失的情形.

3.3 氩气辉纹的电离波特征

综上可知,在氩气辉光放电过程中,亚稳态原子导致的分步电离会引起电离不稳定性,且这种不稳定性会以电离波的形式传播,使得等离子体参数在纵向上起伏波动,从而形成辉纹.现在讨论这种电离波的速度和频率.电离波的速度为[37]:

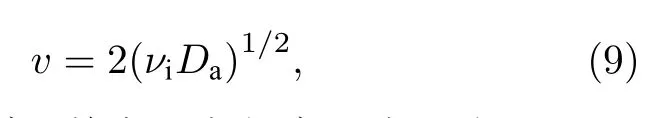
其中νi是电离频率.其中电离频率可表达为

式中,vd是电子漂移速度,它是电场强度E和气压p的函数:

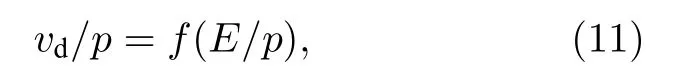
氩气辉光放电中,vd可表达为vd=0.33×106(E/p)cm2·Torr/(V·s).本实验中,腔室气压p=21.22 kPa=159.16 Torr,电极间距d=10 mm,放电电压U=414 V,由此可得出电场强度的表达式为E/p=2.60 V/(cm·Torr).进而可以计算得到漂移速度为0.86×106cm/s.汤生第一电离系数α可表达为α/p≈1.0×10-4cm—1·Torr—1[5].于是,可由(10) 式得到电离频率νi=1.37×104s—1.在辉光放电等离子体是典型的非平衡等离子体,电子温度远大约离子温度,双极性扩散系数满足爱因斯坦关系:

其中µi是氩离子迁移率,kB是玻尔兹曼常数,Te是电子温度.本文中,µi=1.6 cm2/(V·s)[38],利用玻尔兹曼斜率法估算电子温度为0.4 eV.由(12)式可得到双极性扩散系数Da=0.64 cm2/s,并将其代入 (9)式可得到电离波速度约为1.87 m/s.考虑电离波波长λ与条纹间距相等,约为0.15 cm,对应的波数k=2π/λ.电离波频率f=ω/(2π)=kv/(2π)=1.25 kHz.放电条件接近的情况下,与氦气和氮气相比,氩气放电产生的电离波具有更低的速度和频率.表1 列出了几种典型气体的电离波特征.

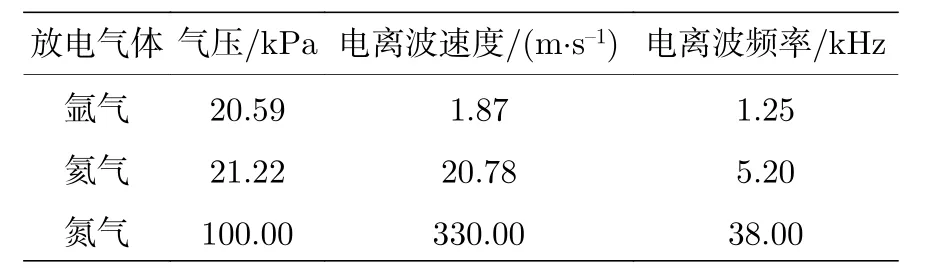
表1 几种典型气体的电离波特征[30,39]Table 1.Ionization wave characteristics of typical gases [30,39].

3.4 氩气辉纹随气压和混入气体的演化和消除

如上文所述,氩气辉光放电条纹对气压十分敏感,可在一定气压范围内存在(20—50 kPa),且随着气压增大,辉纹间距减小,数目增加,如图8 所示.当气压增加到42.51 kPa 时,辉纹变得几乎不可分辨,继续增大气压,辉纹就会演变成为连续的等离子体柱.这是由于随着气压的增大,电子的平均自由程减小,电子与氩原子的碰撞就会更加频繁,氩原子可在更短距离内就可以被激发或电离,因此辉纹的间距减小,数目增加.氩气辉纹的这种随气压演化规律与氦气辉纹的演化规律是一致的[30].

图8 辉纹随气压的形态演化 (a) 28.54 kPa;(b) 32.84 kPa;(c) 37.62 kPa;(d) 42.51 kPaFig.8.Evolution of striations with pressure:(a) 28.54 kPa;(b) 32.84 kPa;(c) 37.62 kPa;(d) 42.51 kPa.

杂质气体是影响辉纹形态另一重要因素,特别是具有较低激发能的双原子分子气体,例如氮气.图9(a)所示为23.17 kPa 时产生的氩气辉纹,图9(b)—(d)分别为逐渐注入氮气对辉纹形态的影响状况.注入极少量的氮气就会对辉纹产生显著的影响,当气压在23.26 kPa (氮气含量为0.4%)和23.37 kPa (0.9%)时,辉纹逐渐被消除,只有在阴极端可观察到辉纹,且氮气含量越高辉纹越易被消除.当通入氮气到气压为23.64 kPa (2.0%)时,辉纹几乎全部消失.本质上,氮气的加入会产生两个重要影响,一是显著地猝灭了亚稳态氩原子,二是改变了电子能量分布函数[40].如前文所述,亚稳态原子的来源一方面来自于基态原子的碰撞激发,另一方面来自于2p 态的辐射跃迁.图10 给出了随着氮气含量的增大,最强发射线696.543 nm (2p态到1s5态的辐射跃迁)的变化情况.从图9 可知,当逐渐加入氮气时,这一谱线的强度有十分明显的减小,这反映了亚稳态原子相当程度地被猝灭.尽管谱线强度不能直接代表Ar(1s5)亚稳态密度,但它的变化可以间接反映亚稳态密度的变化趋势[41,42].亚稳态氩原子导致的分步电离会引起电离不稳定性,这种不稳定的发展会引起等离子体参数的纵向调制,从而形成明暗相间的放电条纹.氮气的加入会猝灭亚稳态氩原子,相应的反应过程为

图9 加入氮气对辉纹的影响 (a) 23.17 kPa;(b) 23.26 kPa;(c) 23.37 kPa;(d) 23.64 kPaFig.9.Effect of nitrogen gas addition to striations at different pressure:(a) 23.17 kPa;(b) 23.26 kPa;(c) 23.37 kPa;(d) 23.64 kPa.

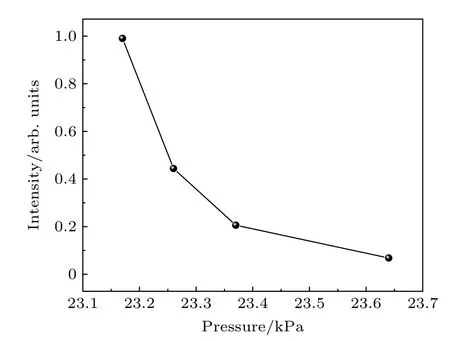
图10 加入氮气对主要发射 线696.543 nm 的影响(a) 23.17 kPa;(b) 23.26 kPa;(c) 23.37 kPa;(d) 23.64 kPaFig.10.Effect of nitrogen gas addition to dominant emission of 696.543 nm:(a) 23.17 kPa;(b) 23.26 kPa;(c) 23.37 kPa;(d) 23.64 kPa.

这一过程被称为激发转移[43].亚稳态氩原子(Ar,1s5)在此过程中被猝灭所需的时间极短,只需2 ns,且Ar (1s5)态的猝灭率高达 3.6×10—11cm3/s[25],这一猝灭率高于 (约为2 倍) 电子碰撞猝灭亚稳态.亚稳态氩原子被大量的猝灭会弱化电离不稳定性,从而使放电过程从条纹模式转变为连续的等离子体柱.需要指出的是,在此放电条件下,由于亚稳态氩原子的能级(11.55 eV)低于氮分子的电离能(15.58 eV),因此潘宁电离过程不存在,亚稳态氩原子的猝灭主要是通过激发转移过程.此外,氮气的加入使电子能量分布函数由非麦克斯韦分布转变为麦克斯韦分布函数,同时电子平均能量变小.当氩气辉纹存在的时候,由于氩气具有较高的第一激发能,电子需被加速到较高的能量才能激发氩原子,放电过程中存在大量的高能电子,这会造成电子能量分布函数的尾巴会发生“扭曲”,电子能量分布函数呈现非麦克斯韦化.当氮气加入时,由于氮分子具有较低的转动、振动激发能(2.0—3.5 eV),且在此能量区间,氮分子与电子碰撞的激发截面非常大,大部分电子被消耗于激发氮气分子[44],这造成电子平均能量减小,电子能量分布函数麦克斯韦化,放电过程向稳定态发展[45],辉纹消失,如图9(d)所示.因此,加入少量的氮气可有效消除放电条纹等离子体,形成连续稳定的等离子体,这对气体激光器等实际应用有重要意义.

4 结论

本文对千帕量级气压下产生的氩气辉纹进行了研究,主要研究了辉纹基本特征,包括电学、光学和电离波特征,辉纹随气压和杂质气体的演化规律;分析了辉纹的产生及消除机制;基于以上分析得到如下结论:氩气辉纹的条纹长度约为1.5 mm,且随着气压升高,条纹的数目增加,条纹长度减小;与氦气辉纹相比,氩气辉纹的条纹长度较小,这与氩气具有较低的激发能有关.此外,发射光谱诊断研究表明,明纹具有更强的发射强度,且主要发射线来自于2p 激发态到1s5亚稳态,这意味着明纹中存在一定量亚稳态氩原子,这些亚稳态原子可能是辉纹形成的重要原因.亚稳态原子具有较高的能量阈值和较长的寿命,使得它们很容易发生分步电离,从而引起电离不稳定性.微扰理论表明,当电离增长率大于双极性扩散率时,这种不稳定就会增强,并以电离波的形式传播,形成辉纹.氩气放电中,电离波的传播速度和频率约为1.87 m/s 和1.25 kHz,这一特征值要略小于氦气辉纹的速度和频率值.放电过程中,加入极少量氮气可有效消除辉纹,使其变成连续的稳定的放电.氮气的加入主要有两个贡献,一是有效猝灭了亚稳态氩原子,减小了分步电离的源头;二是改变了电子能量分布函数,使其趋向麦克斯韦分布,从而放电变得稳定.