三维水平井轨道优化对齐设计模型
李小平,李伟峰,贾红娟,郝世彦
(1.延长油田股份有限公司 志丹采油厂,陕西 延安 716000; 2.延长石油(集团)有限责任公司研究院,陕西 西安 710075; 3.延长油田股份有限公司 勘探开发技术研究中心,陕西 延安 716000)
引 言
三维水平井是井口和各个靶点不在同一个铅垂面内的多目标水平井[1]。在进行轨道设计时,水平段的方位和形态受地质靶点的约束,直井段受造斜点深度的约束[2]。斜井段的轨道形态与参数受工程允许狗腿度的约束,直井段的末端和水平段起点是斜井段的边界。
井眼轨迹的连线不可能只是简单的对接。水平井轨道优化对齐设计就是要实现在限定斜井段狗腿度的情况下,以科学合理的井斜、方位和狗腿度实现相邻井段之间的准确相切[3]。
目前,国内外普遍采用的三维水平井轨道设计方法,缺少关于井眼轨道曲线的严格数学表达,需要使用复杂的数值迭代或积分运算求解,不易于被普通技术人员所掌握,因此设计简单直接的轨道数学模型和易于理解的计算方法,避免复杂的迭代和积分求解,不仅可以大幅提高轨道设计效率,而且更有利于设计人员和现场施工人员直观理解和优化轨道参数。
1 三维水平井轨道设计模型
在三维空间内建立水平井轨道设计的空间模型。如图1所示,横轴为水平面东西坐标,用+E(东)、-W(西)表示,向东(E)为正,向西(W)为负,纵轴为平面南北坐标,用+N(北)、-S(南)标识,向北(N)为正,向南(S)为负,Z轴表示垂深,向下为正。

图1 水平井轨道设计模型示意图
1.1 模型参数
井口:O,O点井斜为0°,无方位;
造斜点:Z,Z点井斜为0°,无方位;
第一圆弧段末端,同为稳斜段起点:C,井斜角αab,方位角φab,待求解;
稳斜段末端,同为第二增斜段起点:D;
第二圆弧段末端,同为水平段起点:A;
水平段末端:B;
其余参数:ΔN为南北坐标增量,m;ΔE为东西坐标增量,m;ΔD为垂深增量,m;D为垂深,m;L为井深或长度,m;ΔL为井深增量,m;α为井斜角,(°);φ为方位角,(°);γ为井眼曲率,(°)/30 m;R为曲率半径,m;下标a、b、c、d、z、o即水平井A、B、C、D、Z、O的相应位置点。
1.2 轨道设计算法
根据上述模型,Z点为造斜点,属已知条件。A、B点为水平段靶点,坐标及垂深为已知条件[4]。ZC圆弧段长度Lzc未知、DA圆弧段长度Lda未知,CD稳斜段长度Lab及方位角φab未知,CD稳斜段井斜角αab是Lzc的线性函数。所以轨道设计的问题,就转化成了已知造斜点、靶点、第一、第二圆弧段全角变化率(狗腿度)的情况下,求解圆弧ZC、DA长度及直线CD段长度和方位角的问题,未知参数为4个。
第一步:根据水平段A点与B点已知垂深,计算水平段井斜角
(1)
根据A点与B点坐标值,计算井斜方位角φ(以正北为起点),方位角函数取值用反正切函数表示:
(2)
(3)
当Nb-Na=0时,Eb≠Ea。如果Eb>Ea,表明水平段自西向东,水平段方位角φab=90°;如果Eb 第二步:计算靶前距,设定造斜点。根据靶前距估算不含稳斜段的全角变化率γ。通过靶前距估算全角变化率时,需假定从造斜点Z至水平段A点为一条理想空间圆弧曲线(可用靶前距对全角变化值进行初步估算),采用最小曲率法[5-6],估算空间圆弧曲线的全角变化率 (4) 那么估算狗腿度 (5) 第三步:试算双增斜井眼曲率γzc和γda。γzc和γda可采取试错法不断修正,由于理想空间圆弧曲线的γ在取值时,并不考虑稳斜段的影响,只是一种近似解,所以,可以根据双增轨道模式,初步设定实际狗腿度γzc和γda都略大于γ。 一般经验是:当需要实现压低造斜点时,可取两段的狗腿度γzc略大于γda,那么,第一圆弧段(ZC)和第二圆弧段(DA)的狗腿度分别为[7-10] γzc=γ+i,i建议取1~2; (6) γda=γ+j,j建议取0~1。 (7) 当需要采取常规双增式轨道设计时,可取γzc略低于γda,即 γzc=γ+j; (8) γab=γ+i; (9) γzc=arccos[cosαozcosαcd+sinαozsinαcd· cos(φcd-φoz)] ; (10) γda=arccos[cosαcdcosαda+sinαcdsinαda·cos(φ-φcd)]。 (11) 第四步:计算不同井段的坐标增量。第一圆弧段,即圆弧ZC段的垂深增量ΔD、南北坐标增量ΔN、东西坐标增量ΔE分别为 (12) sinαcdcosαcd); (13) sinφcd)。 (14) 式中, (15) 第五步:圆弧段DA的垂深D、南北坐标N、东西坐标E的增量分别为 (16) (17) (18) 第六步:从井口至A点的垂深增量、东西坐标增量、南北坐标增量为已知值,则 ΔDzc+ΔLcdcosαcd+ΔDda=|Da-Dz|; (19) ΔNzc+ΔLcdsinαcdcosφcd+ΔNda=|Na-Nz|; (20) ΔEzc+ΔLcdsinαcdcosφcd+ΔEda=|Ea-Ez|。 (21) 第七步:合并方程(10)、(11)、(19)、(20)、(21),方程组中只有4个未知参数,5个方程,可直接求解Lzc、Lab、Lda、φab。 第八步:根据方程结果,即可得出造斜率、方位扭转率等全部输出参数。如取值不合理,可进一步调整γzc和γda,重复式(6)—式(21)计算步骤即可。 为证实上述算法的精确性,以一口三叠系延长组长6层三维水平井为例,实例井靶点参数见表1。 表1 实例井靶点参数 2.2.1 第一次验证 假定造斜点位置:250 m。 第一步:根据水平段A点与B点已知垂深,计算水平段井斜角 计算水平段方位角φ,方位角函数取值用反正切函数,即 第二步:预设造斜点250 m,计算靶前距(A点相距井口的水平位移) 空间圆弧曲线的全角变化值 则估算空间曲线的全角变化率(狗腿度) 第三步:由于该井靶点埋深较浅,需要实现压低造斜点,因此取γzc略大于γda,即 γzc=(γ+1.17)=6.04°/30 m, γda=(γ+0.67)=5.54°/30 m。 第一圆弧段、第二圆弧段全角变化值为 建立等式 (22) 第二圆弧段狗腿度满足: sin 90°cos(36.87°-φcd)], (23) 简化为 (24) 第四步:建立第一圆弧段的坐标增量方程,圆弧段ZC的垂深D、南北坐标N、东西坐标E的增量分别为: (25) (26) (27) 第五步:圆弧段DA的垂深D、南北坐标N、东西坐标E的增量分别为: (28) (29) (30) 第六步:从井口至A点的垂深增量、东西坐标增量、南北坐标增量为已知值,将式(25)—式(30)代入式(19)—式(21)则 ΔDzc+ΔLcdcosαcd+ΔDda=|Da-Dz|=330; (31) ΔNzc+ΔLcdsin|αcdcos|φcd+ΔNda=|Na-Nz|=300; (32) ΔDzc+ΔLcdsin|αcdcos|φcd+ΔEda=|Ea-Ez|=200。 (33) 第七步:合并方程(24)、(25)、(31)、(32)、(33),方程组中只有4个未知参数,4个方程,可借助Mathcad求解Lzc、Lab、Lda、φcd。 通过上述计算方法,当γzc=6.04°/30 m,γda=5.54°/30 m时ΔLzc=240.62 m,Lab=30.12 m,Lda=273.46 m,αcd=48.44°,φcd=68.65°。 那么,采用行业普遍使用的兰德马克系统,预设同样的造斜率和造斜点,计算双增剖面下的轨道参数,结果见表2。 从表2可以看出,第一圆弧段长度Lzc=490.62-250=240.62 m;稳斜段长度Lcd=520.74-490.62=30.12 m;第二圆弧段长度Lda=490.62-250=240.62 m;稳斜段井斜角αcd=48.44°;稳斜段方位φcd=68.65°。设计模型的计算结果与Landmark Compass软件计算的双增剖面参数一致。 表2 采用Landmark Compass软件计算的双增式井身剖面参数(γzc=6.04°/30 m,γda=5.54°/30 m) 2.2.2 第二次验证 为进一步验证设计模型的准确性,预设γzc=7°/30 m,γda=5.5°/30 m时,采用文中的计算方法,求解结果为:第一圆弧段长度ΔLzc=174.03 m,稳斜段长度Lcd=50.40 m,第二圆弧段长度Lda=317.16 m,稳斜角αcd=40.61°,稳斜段方位角φcd=72.69°。 采用Landmark Compass软件计算的轨迹见表3。 表3 采用Landmark Compass软件计算的双增式井身剖面参数(γzc=7°/30 m,γda=5.5°/30 m) 由表3可知, 第一圆弧段长度Lzc=424.03-250=174.03 m;稳斜段长度Lcd=474.43-424.03=50.40 m;第二圆弧段长度Lda=791.59-474.43=317.16 m;稳斜段井斜角αcd=40.61°;稳斜段方位角φcd=72.69°。所以,二者计算结果仍然是吻合的。 (1)斜井段的曲线形态和轨道参数是三维水平井轨道设计的核心问题。优化对齐设计的目标就是在限定斜井段狗腿度的情况下,以科学合理的井斜、方位和狗腿度实现相邻井段之间的准确相切。 (2)通过本文的研究,将三维水平井的轨道设计问题转化成了一个多元一次方程组的求解问题,只要确定了造斜点、靶点、预设好第一圆弧段和第二圆弧段的狗腿度,井眼轨道参数的解就具有唯一性,计算结果与Landmark双增剖面设计的结果一致。 (3)本文所形成的计算方法,第一圆弧段的狗腿度与造斜率一致、第二圆弧段造斜率恒定,方位扭转率不恒定,距离水平井A点越近,方位扭转率越小,可以实现在小井斜段多扭方位,大井斜段少扭方位,有利于现场井眼轨道控制和水平段矢量中靶。
2 实例验证
2.1 实例井靶点参数

2.2 验证过程及结果
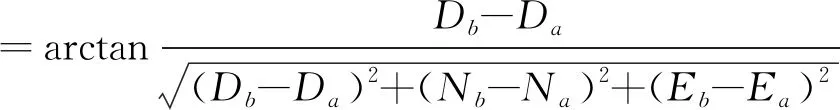




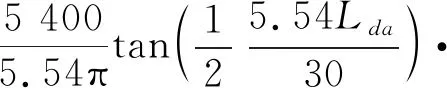
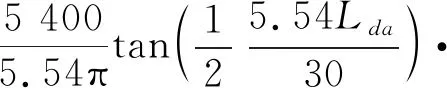


3 结 论

