基于熵权-逼近理想解排序法-多群体问询的山区农村公路无信号交叉口安全风险评估模型

任一玮， 刘星良*， 刘瑜， 张子乾

(重庆交通大学交通运输学院， 重庆 400074; 2.贵州省遵义市播州区交通运输局， 遵义 563100)

截至2020年底，中国农村公路总里程达438.2万km，占公路总里程的84.3%，等级公路比例达到95%以上[1]，但农村公路建设依旧存在着道路等级较低，道路环境复杂、养护意识欠缺、交通安全设施匮乏等问题，让许多农村公路成为了事故多发的“重灾区”，具有事故总量大、死亡率高、重特大事故时有发生的鲜明特点，因此山区农村公路交通安全引起了相关部门和专家学者的高度重视。根据中国交通事故统计分析结果可知，发生在交叉口的事故数约为总事故数的30%，发生在山区农村公路交叉口路段的事故占据事故总数的11%[2]。由于山区农村公路交叉口范围与面积较小、建养资金紧缺等现实问题，大量交叉口并无信号控制，有些位于相对偏远的山区农村公路交叉口甚至成为无信号、无标志、无标线的“三无”交叉口，机非混行现象严重，具有重大安全隐患。因此，针对风险隐患提出可靠的安全风险评估模型，具有一定程度的实践价值。

当前，研究学者主要针对城市道路信号交叉口交通安全风险进行了改善与评估研究。Yao等[3]运用改进社会力模型，考虑行人屈服准则，分析了城市干道交叉口安全风险；Vuong等[4]提出基于信息熵和层次分析法，利用交通冲突和云模型构建混合交通条件下交叉口安全评价模型；Nopadon等[5]提出基于视频的交通冲突分析构建评价交叉口碰撞风险模型；赵晓华等[6]提出一种基于导航数据的进口道风险与交叉口相关属性间量化关系的挖掘方法,从而实现交叉口进口道风险的评估与诊断。基于以上研究发现，国内外学者对城市干道交叉口普遍采用模型定量、实际状况定性的手段来评估风险隐患，对定量研究不足的山区农村公路无信号交叉口安全评估具有指导价值，但仍存在不足。一是定性评估方面，常采用的专家打分法具有一定局限性。山区农村公路与城市道路交叉口风险隐患特征不尽相同，其环境复杂，事故种类多样，往往伴随一定偶发性，专家人员很难短时间内对道路构成成分、事故致因、安全影响因素做出有效判断，且评估人员群体较为单一，数量较少，缺少多角度、多方面的综合因素分析，存在有偏估计的可能。二是定量评估方面，国内外学者提出了基于灰云模型、冲突极值模型、交通冲突理论等分析方法对城市干道交叉口进行安全评价，但以上方法对于数据匮乏的山区农村无信号交叉口难以实现。

基于此，现基于熵权逼近理想解排序法(technique for order preference by similarity to an ideal solution，TOPSIS)法对山区农村无信号交叉口安全风险进行建模，说明特征指标选取原因及标准，通过多群体问询的调查方法，改善原有方法定性评价的不足，得出客观的风险矩阵，从而计算不同风险指标熵权，运用加权广义马氏距离与欧式距离贴近度的比较，给出最优综合得分，提出基于山区数据匮乏环境下无信号交叉口安全风险的评估模型，最终根据风险隐患的分析结果从而给出相应的解决方案。

1 山区无信号交叉口安全风险特征指标体系构建

建立无信号交叉口风险模型的科学、合理性决定了事故分析、改善结果的可靠性与准确性。在安全特性、实地勘察的基础之上，围绕着事故多发路段进行了道路安全分析与调研，根据事故路段最典型、普遍的风险特征，筛选并总结出9个最为影响山区无信号交叉口安全的风险特征指标。

(1)平均日交通量(average daily traffic，ADT)。该指标可衡量山区农村无信号交叉口设施的需求，用来评价现状交通量与道路通行能力的相互适应性，从而确定是否需要增加路面宽度、车道条数或使用其他改善措施来增加通行能力，是无信号交叉口安全隐患的重要影响因素。

(2)速度标准差。在事故统计中发现，车速平均值越高，速度的离散程度越大，事故发生的概率越大[7]。对于农村山区无信号交叉口而言，汽车通过交叉口时速度的稳定性，对事故的发生有显著影响。根据调查发现，通过山区农村公路无信号交叉口的车辆速度差异大，在遇紧急事件时，快车容易从后方追尾前车或与两侧路口驶出车辆发生严重横向碰撞，造成财产损失与人员伤亡，故选取速度标准差作为特征指标。

(3)路权分配比。机动车与非机动车混行是山区农村公路无信号交叉口的典型问题，附近村民横穿道路或驾驶农耕车辆与机动车抢行的现象频繁，路权的分配不合理严重影响交叉口交通安全，这种混合交通类型需要作为参数进行评定。

(4)支路纵坡坡度。支路纵坡坡度较大，此类长大下坡路段容易造成车辆车速过快，从而高速通过无信号交叉口，视距范围缩小，反应距离增大，具有风险隐患。其原因大都由于道路建设资金不足，通过减少填挖量的方法节约成本，导致有些支路纵坡坡度超过了10%的限制，带来严重安全隐患。

(5)线形设计。在接入无信号交叉口的干路上，设有陡弯、急坡或是长直线线形的无信号交叉口事故率明显上升。其中陡弯、急坡导致支路与干路交叉的角度与支路平曲线半径过小，车辆的驾驶稳定性受到强烈干扰[8]；长直线线形无疑会导致车辆速度过快、驾驶员视觉疲劳等不良影响，故选取线形设计为特征指标。

(6)视距情况。视距目的是保障行车的安全性，视距不良取决于设计速度与平面线形、纵断面线形等，无信号交叉口对以上指标的忽视，使得其会车视距无法满足停车视距的两倍以上，路段每公里视距受限次数大大提高，造成视线有效距离远小于停车视距的现象，从而增加了因避险不及时导致的交通事故[9]。如表1所示。

表1 视距受限次数与事故数关系

(7)标志标线状况。由于山区特殊的气候环境因素，无信号交叉口交通标志标线腐蚀、褪色等现象严重，有些交通标志标牌歪斜，对驾驶人员的约束与导向作用削弱。在一些与急弯、连续下坡相连接的交叉路口，缺少交通标志给予驾驶人道路信息以及设置指路标志距离不合理的现象都会导致驾驶人反应不及时，故将交通标志标线的完整与合理程度设为特征指标。

(8)视线诱导设施。视线诱导设施的目的主要是提升驾驶员视认程度，但山区农村公路无信号交叉口普遍未设置视线诱导设施，对于夜间、大雾或雨雪等极端天气下行车的驾驶人具备一定风险。

(9)安全防护设施。山区农村公路路侧防护设施需要根据环境变化、道路线形、防护工程等条件进行选用。针对山区农村公路无信号交叉口的安全防护设施问题主要是路侧护栏端头处缺少有效的防护，从而存在车辆失控撞击端头的风险。

针对上述9种不同性质的特征指标，依据其引发事故风险的内在联系，归纳了3种影响山区无信号交叉口交通事故发生的关键性上位要素，分别是交通特性类风险、山区农村道路条件类风险、交通安全设施类风险。考虑到指标的可实现性与逻辑层次性，最终建立山区农村无信号交叉口风险模型，包括3个一级指标和9个二级指标，如图1所示。

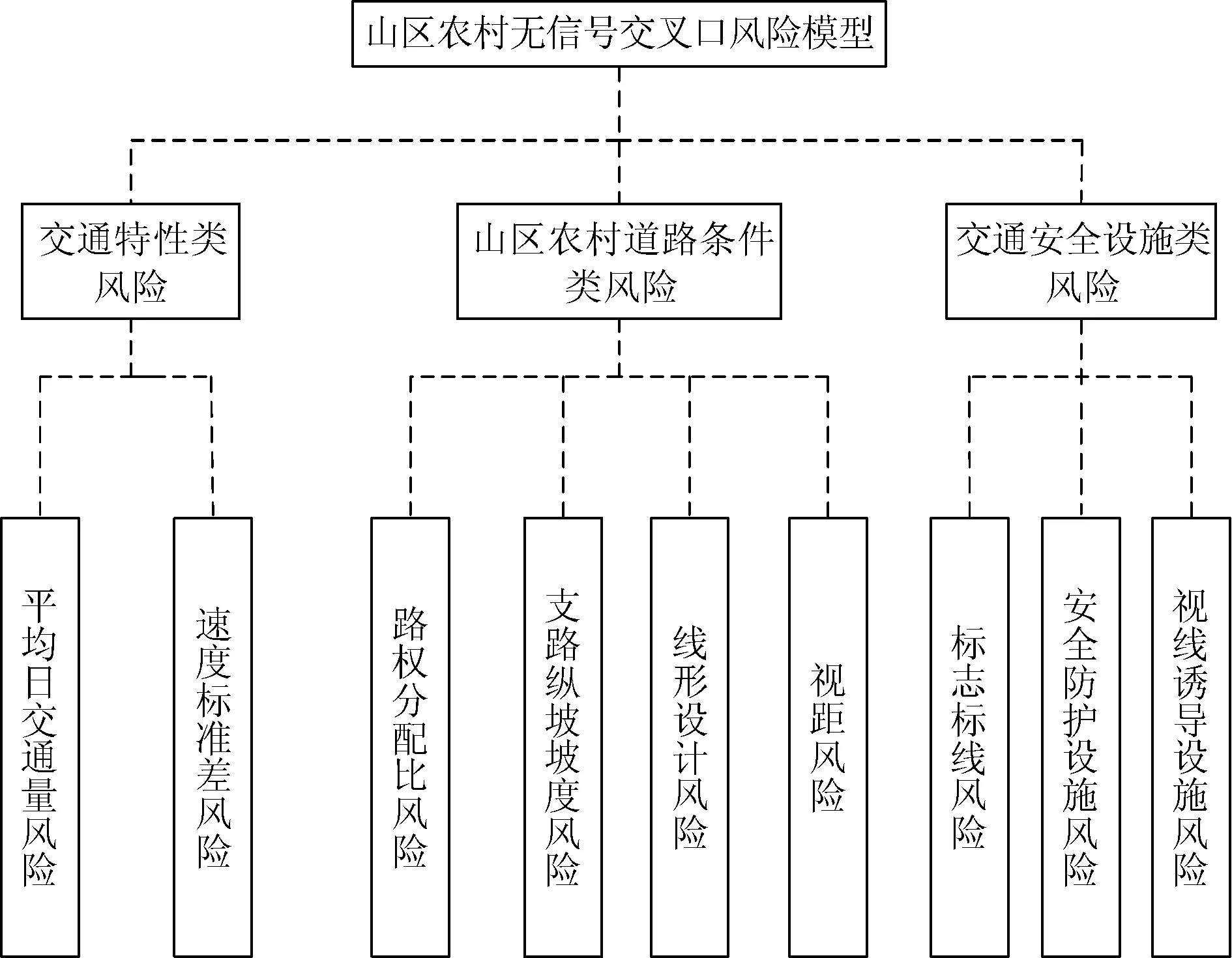
图1 山区农村无信号交叉口风险评估模型Fig.1 Risk assessment model of unsignalized rural intersections in mountainous areas

2 基于加权广义马氏距离的熵权TOPSIS法无信号交叉口模型构建

2.1 熵权TOPSIS模型

熵权TOPSIS法是一种可以客观反映模型指标离散程度以及其重要性的方法，从而减少人为主观因素对结果的影响。其主要目的是评价对象与最优目标值的远近，通过信息熵确定指标权重，指标信息熵值越小，其相应的效用值就会越大，权重占比也就越大。其次，通过对熵权TOPSIS法进行改进，使用加权广义马氏距离代替欧式距离表示更为准确的加权距离，得出各方案与最优方案的贴近程度，最终进行综合评价。

2.1.1 构建标准矩阵并归一化

根据调查对安全风险数据进行标准化处理。设定m个对象，n个风险指标。其初始矩阵F可用式(1)表示。

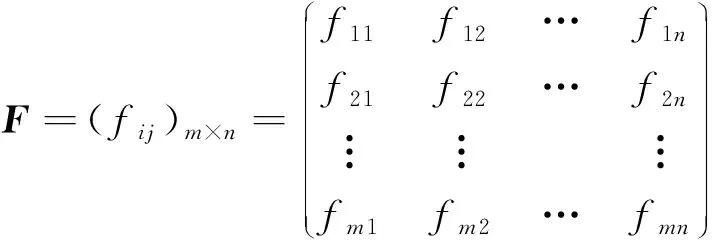
(1)

式(1)中：fij为原始安全风险，取1～5，5分为极大风险，1分为安全。

然后对指标进行归一化处理，且因风险指标均为负属性指标，故采用最大最小归一化方法，计算公式如式(2)所示。

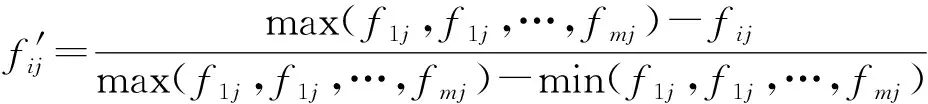
(2)

此时得到归一化后的矩阵为

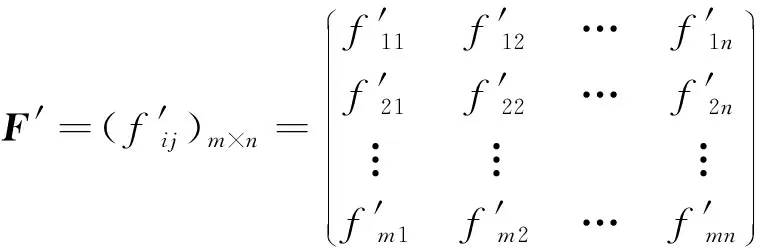
(3)

2.1.2 求解各指标信息熵

根据信息熵的定义求解各指标信息熵，计算公式如式(4)所示。

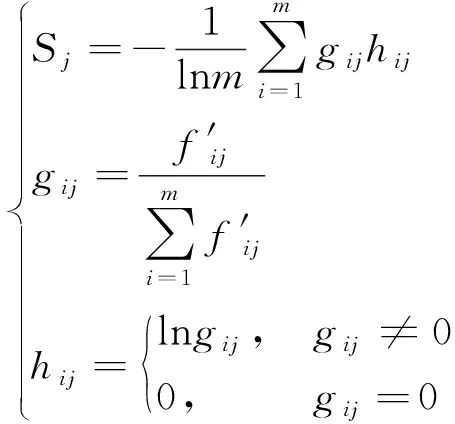
(4)

2.1.3 确定各指标熵权

各指标熵权计算公式如式(5)所示。

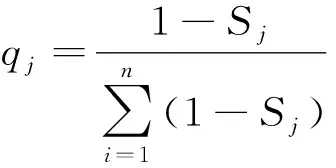
(5)

计算所有指标熵权，得出指标权重的行向量Q=(q1,q2,…,qn)。此时，所得出的权重可直接用于计算加权安全风险值，运用优劣解距离TOPSIS法对安全风险进行综合评估。TOPSIS法能充分利用原始数据的信息，精确地反映各个方案间的不同，将不同属性的各个指标综合为具有代表性的单一指标，从而方便排序，得出最优的方案[10]。

2.1.4 原始数据正向化

由于选取的调查方案中安全风险指标均为负向指标，又称极小型指标，也称成本型指标，其数值越小，实际道路安全性越高，为了统一计算与方便比较，一般将极小型指标、中间型指标、区间型指标全部转化为极大型指标，这个过程称为正向化，计算公式如式(6)所示。

aij=max(f1j,f1j,…,fmj)-fij

(6)

经过上述处理，得到正向化后的矩阵为

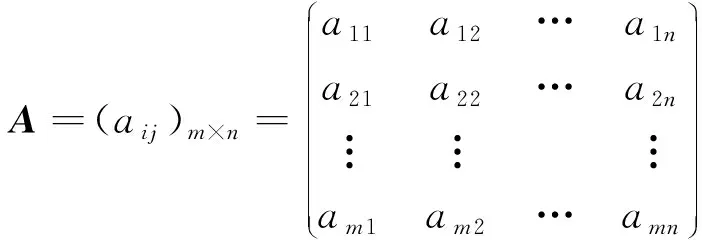
(7)

式(7)中：aij为正向风险值。

由于对各指标都采用风险值的方法衡量，所以量纲相同，直接将所得正向风险矩阵进行标准化处理，公式如式(8)所示。

(8)

经过计算，得

B=[B1,B2,B3,…,Bm]T

(9)

2.1.5 计算加权距离

首先，需要确定正负理想解，正理想解是B矩阵每列元素中的最大值所组成的向量。负理想解同理，即

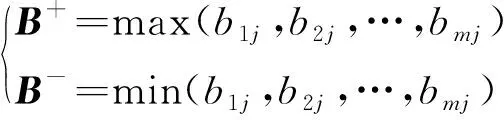
(10)

其次，计算加权距离。一般计算距离时，采用欧式距离进行运算，其代表在m维空间中两个点的真实距离，但是欧式距离将方案中不同指标之间的差别同等看待，这一点在无信号交叉口安全风险预测模型中稍有不妥，对于风险预测模型中不同属性指标应考虑到其内部各种特性之间的联系，比如速度与视距、坡度、线形等都具有潜在关系，所以，选择加权马氏距离公式作为欧式距离的优化加权距离计算公式[11]。

(11)

2.1.6 计算贴近度

计算各无信号交叉口对于理想解的贴近程度Di，计算公式为

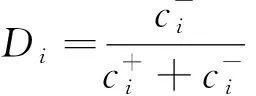
(12)

至此完成熵权TOPSIS法全部步骤，对其结果进行评分，评分数值越大，无信号交叉口安全性越强。

2.2 基于多群体用路者的调查问卷分析

基于上述模型分析，现选取重庆市铜梁区多条农村公路进行调研，发现多数山区公路交通事故与主干路无信号交叉口、机耕道接入口安全风险有关，故选取路段S302铜梁城区至侣俸段某分流道路进行细化研究。其全长8.5 km，共有54个交叉口和机耕道接入口，其中53个均为无信号交叉口，交通安全事故多发。选取具备典型安全问题的8个无信号交叉口进一步分析，为消除专家主观评分的缺陷，提出多群体问询法，步骤如下。

步骤1确定打分人群与人数，如表2所示。打分总人数为30～50人，专家占比约40%，驾驶员与附近村民约占60%。

步骤2确定调查范围。通过对道路以及无信号交叉口行人与非机动车问询发现，使用道路的村民大多聚集在道路周边0.5～3 km范围以内，故对此范围内常使用道路的村民与驾驶员进行无信号交叉口安全风险问询。

步骤3设计与分发调查问卷。针对不同人群的调查问卷设计7个主观题目，7个题目主要与特征风险指标对应[式(5)～式(12)]，考虑到社会背景、文化程度等因素，对不同人群问询的侧重点不同，专家的问卷设计是基于专业素养的针对性评价，问询语言较为专业；对驾驶人的问卷设计是基于《公安部道路交通安全研究中心》驾驶人类型的主观评价，问询语言贴近生活[12]；对附近村民的问卷设计是基于农村公路无信号交叉口实际交通安全问题的广泛评价，问询语言朴实，易于理解。

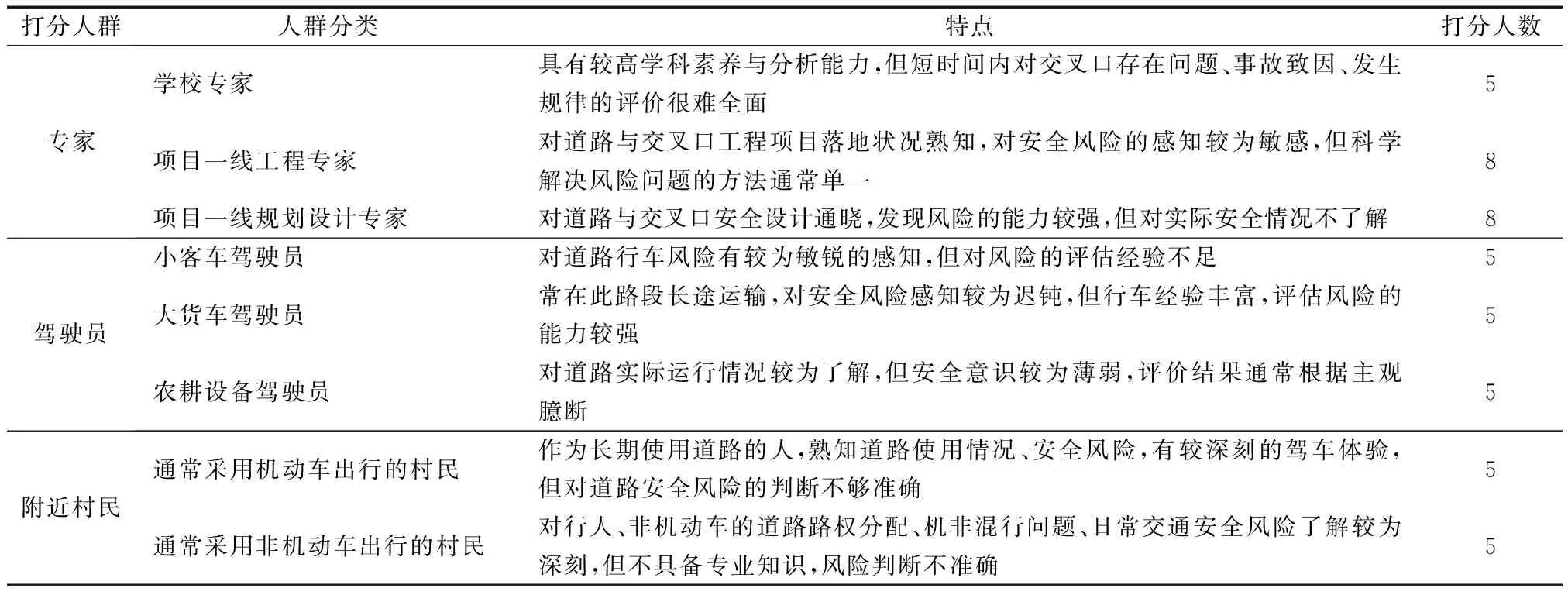
表2 打分人群划分及特点

最终，通过对三类人群的问询，基于测速、监控、实地调查问卷的方法对无信号交叉口风险要素统计分析，并得到三类人群的评分数据，共计收集调查问卷96份，有效问卷94份。

2.3 实践验证

对所获得数据采用熵权TOPSIS法分步骤处理。首先，对8个无信号交叉口收集的94份问卷中9个二级指标按照专家、驾驶员、附近村民分别求出算术平均数，之后根据专家评价意见40%、驾驶人30%、附近村民30%的权重计算每个指标的最终加权平均数，得到表3；将表3转化为矩阵，代入式(2)、式(4)、式(5)中，得到8个无信号交叉口安全风险指标的信息熵和熵权，如图2所示。通过图2得出，线形设计、视距、支路纵坡坡度3个指标权重占比较大，说明以上指标对山区农村公路无信号交叉口的安全影响程度相对较高，山区农村公路交叉口进口道线形存在风险隐患问题较为突出，安全风险不确定性大，如陡坡、急弯、长直线等常见线形问题。线形不良的同时往往会存在“连锁反应”，经常引发交叉口视距问题，尤其是在农村公路无信号交叉口车速较快、支路坡度较陡、路侧环境对视线遮挡严重的现实情况下，线形、视距、坡度三者之间形成了交融复杂的安全风险关系，本文模型将复杂关系量化，对危害无信号交叉口安全的风险指标权重进行排序，从而指导后续重点安全风险改善工程。通过式(6)和式(8)，得到标准化、正向化处理后的正向安全风险指标。得出标准正向安全风险指标的矩阵后，通过式(10)判别出正、负理想解。采用加权广义马氏距离，用MATLAB计算出协方差伪逆矩阵Σ+。最终，将伪逆矩阵代入式(11)计算加权广义马氏距离，最后通过式(12)得到加权广义马氏距离与欧式距离关于理想解的贴近度，给出综合得分，如图3所示。

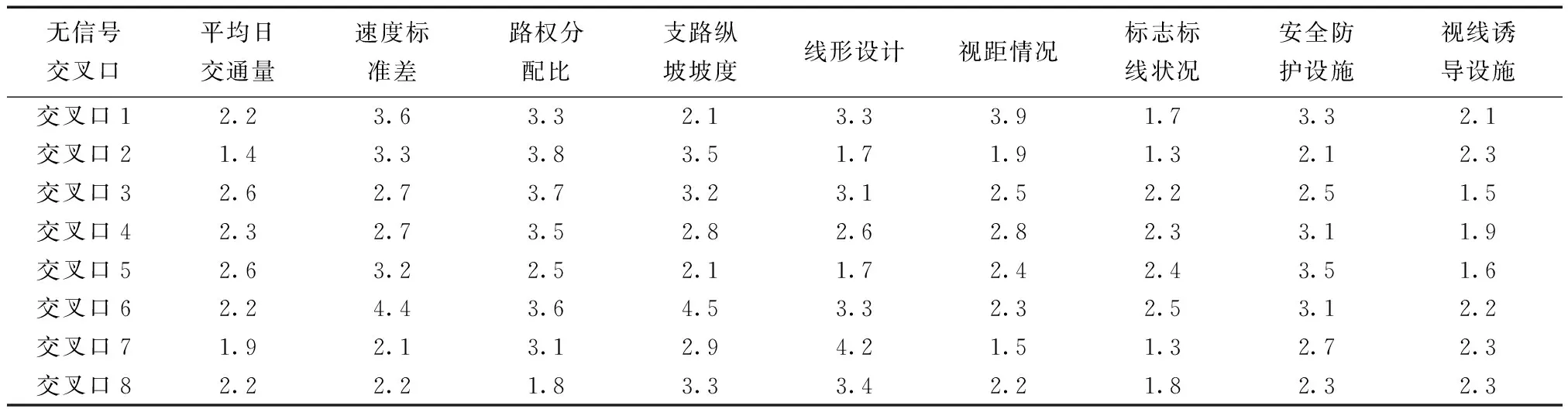
表3 风险指标评分表Table 3 Risk index evaluation table

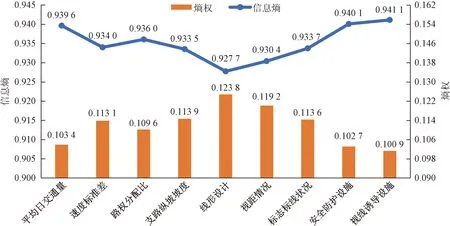
图2 风险指标信息熵与熵权Fig.2 Information entropy and entropy weight of risk indicators

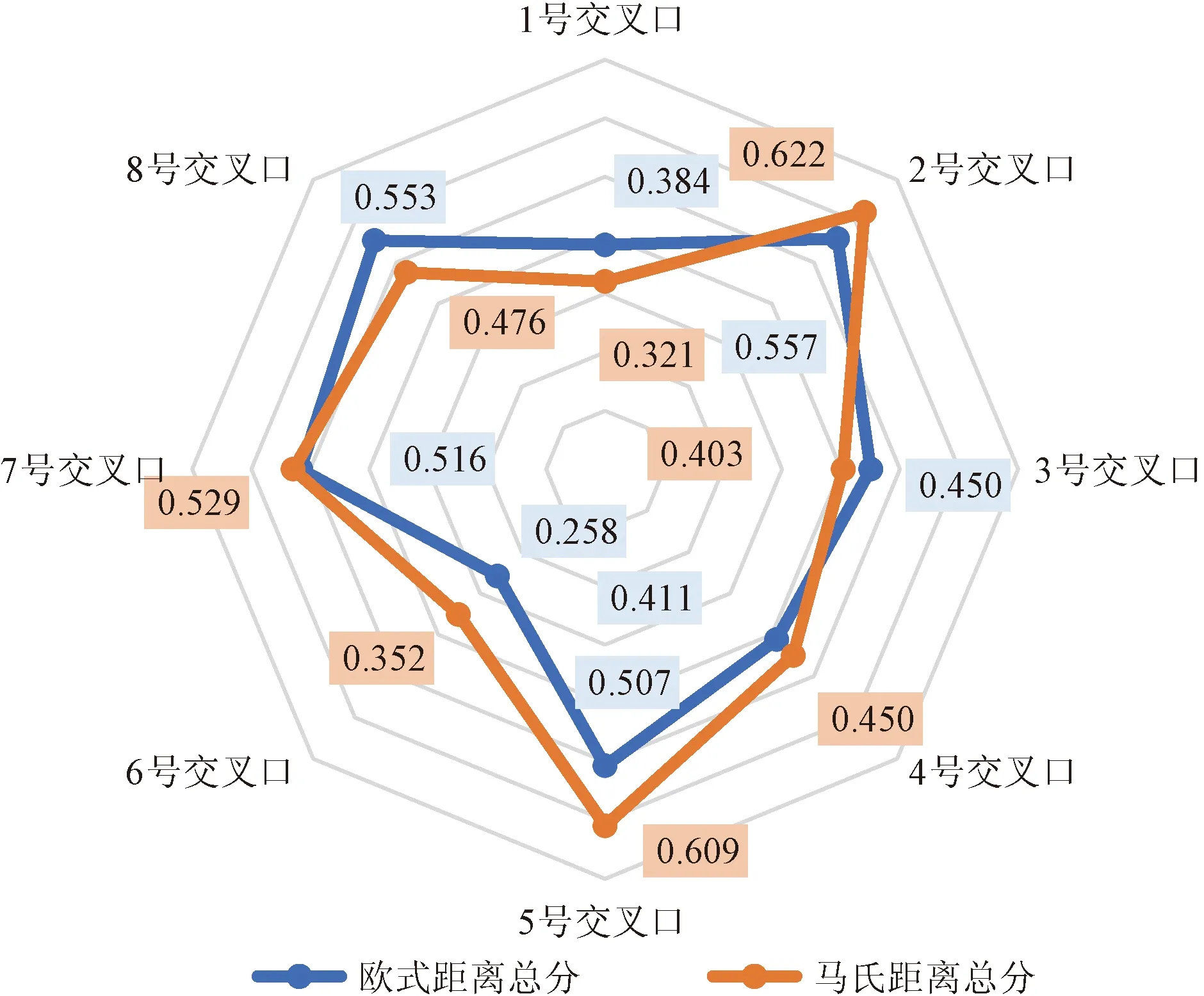
图3 加权广义马氏距离与欧式距离贴近度的综合得分Fig.3 Comprehensive score of closeness degree between weighted generalized Mahalanobis distance and Euclidean distance

依据图3，可直观看出两种方法对安全风险的预测重叠面积较大，趋势接近，说明方法拟合度较高。相同点有无信号交叉口6对理想解的贴近度为最低，表明两种距离都预测其安全风险为同类无信号交叉口中的最高。交叉口2对理想解的贴近度最高，交叉口4与交叉口5分别位于第三位与第五位，仅交叉口1、3、7、8通过两种距离求法所获总分排序不同，但总体排序相差不大，说明本文方法具有一定科学性、可行性。

2.4 对比分析

采用加权广义马氏距离与传统欧式距离贴近度综合得分做对比的方式，求出的无信号交叉口安全风险评估指标数值，如图3所示。两种距离计算方法同时得出交叉口6、1、4为风险最高的3个无信号交叉口，交叉口2为风险最低的无信号交叉口，说明不同计算方法下模型对于总体风险极值的评估具有准确性，对无信号交叉口风险大小的综合排序具有科学性，结合实际工程调研，发现模型对无信号交叉口风险的综合评估与事故数据和专家论证结论基本一致，充分说明了本文模型的有效性。

2.5 改善措施

将数据分析结果与实际调研情况进行匹配，发现无信号交叉口6处确实存在较大安全风险，其于两月内发生3起交通事故，造成8人受伤，以附近村民非机动车或农耕车辆与道路主线汽车发生碰撞的事故形式为主，如表4所示。

经过调查分析，事故主要致因为线形不良，主路汇入无信号交叉口前约有1 km长直线形，导致车辆普遍超速。主干路驾驶员视距受到两旁山丘影响，对支路的有效视野范围变窄，视距不良问题突出，且主路与无信号交叉口衔接的支路纵坡坡度趋近于10%，车辆驶入交叉口时车速难以控制，同时，在进入无信号交叉口前800 m，主路上无任何限速标识标牌、减速标识标牌和其他标识标牌，仅在交叉口前10 m处设置十字路口标识。标牌位置设置不合理，不仅没有给予驾驶员反应时间，还会遮挡驾驶员对交叉口支路驶出车辆距离的判断，在夜晚或雨雾的环境下，视距不良的问题更为严重。最终，调查分析后发现事故指标熵权排序与事故主要致因排序基本相同，间接证明了模型的实践可行性。无信号交叉口6现场勘察如图4所示。

平面路段长直线在道路建设阶段应采用线形灵活组合的方式避免发生，可与大半径凹形竖曲线组合，在实际工程改善时，常用来限制线形不良带来的负面影响[13]。为控制速度，对纵坡较大的无信号交叉口支路铺设20 m减速震荡标线，以使下坡车辆降速，主路双向车道铺设50 m减速震荡标线，强制降低主路车辆行驶速度；为改善视距，在主路的交叉路口，安装视距不良预警系统，如图5所示，通过LED显示屏警示主路与支路车辆，前方来车，减速慢行，规避支路口车辆交汇时存在的高风险驾驶行为，对驾驶员进行提示与视线诱导，从而让驾驶员谨慎驾驶；为改善交通标志对驾驶员的信息传递效果，将十字路口标志后移20 m，并在主路双向车道上安装40 km/h限速标志，2个爆闪灯，2块慢行标志，内容为“前方路口，减速慢行”，更直观地提醒驾驶员减速。综合处置如图6所示。

表4 铜梁区省道302线某分流路交通事故统计表

图4 无信号交叉口6处现场勘察实景Fig.4 Real scene of field investigation at No.6 signal-free intersections

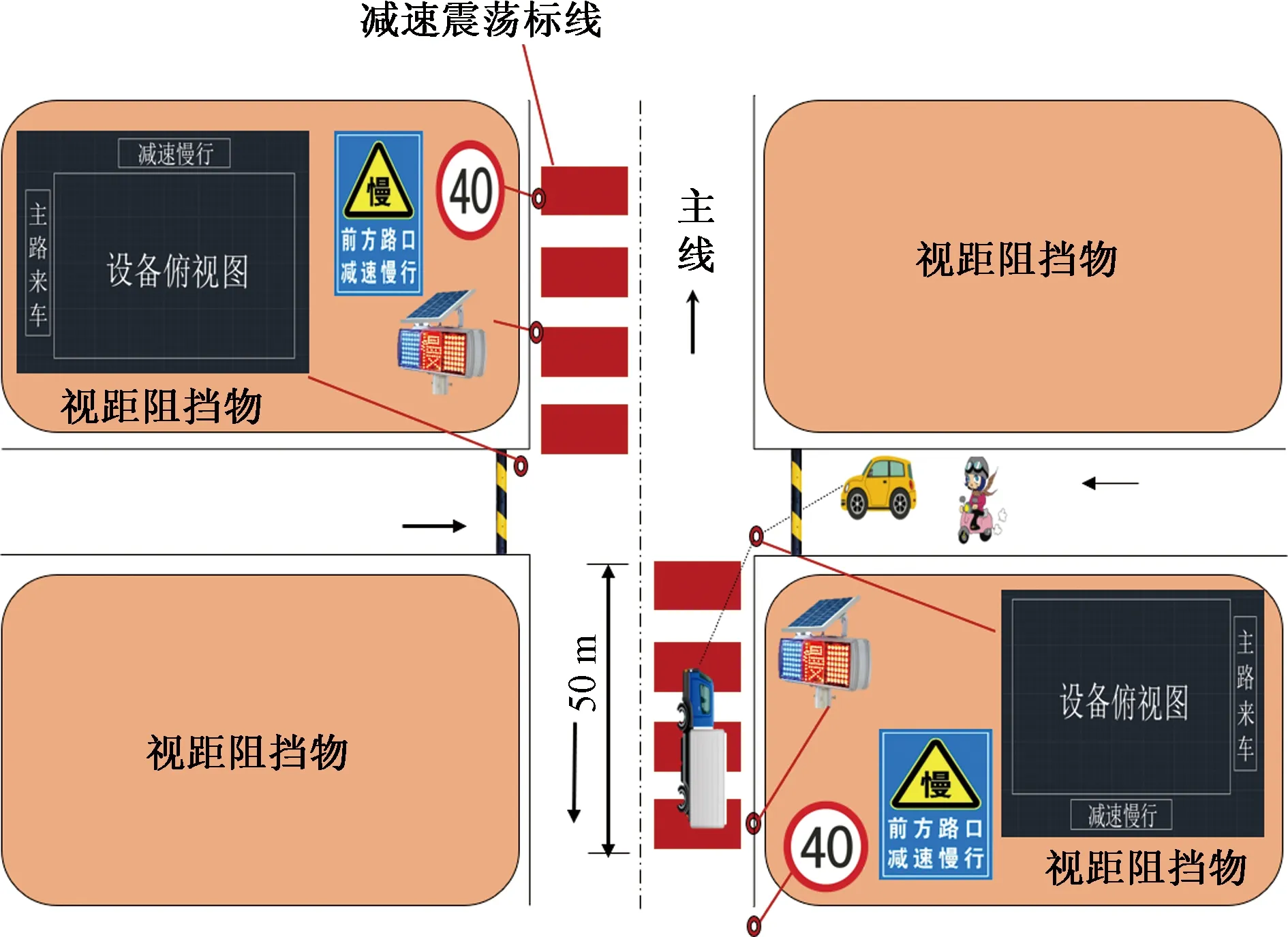
图5 十字交叉口综合处置示意图Fig.5 Comprehensive disposal diagram of intersections

3 结论

山区农村公路无信号交叉口通常被视为农村道路事故黑点，也是山区农村公路交通安全的痛点与难点问题，在这一区域交通事故总量大，重大事故常有发生。建立了山区农村公路无信号交叉口安全风险评估模型，为定量研究山区农村无信号交叉口安全风险隐患提供了新思路。

(1)在查阅大量相关文献、实地调研、问卷调查的基础之上，综合考虑了中国山区农村无信号交叉口的普遍性安全风险与安全隐患，考虑到健全农村公路无信号交叉口的保护与安全防治手段，以此为目标建立了山区农村公路无信号交叉口安全风险评估模型，其中包括3个一级指标和9个二级指标。

(2)创建了基于评价体系的多渠道、多元化、多群体的问询方法，获取客观真实的交叉口安全风险指标数据，建立了基于熵权TOPSIS的山区农村公路无信号交叉口安全风险模型，避免了数据的主观性，能很好地判断不同指标的综合影响程度，使特征指标权重的判定更加科学与方便。

(3)通过对比欧式距离与广义马氏距离得出的贴近值，检验了自身模型的准确性，并与实际工程相结合，对综合得分较低、安全风险大的无信号交叉口逐个分析，发现主要致因排序与风险指标熵权排序基本相同，从而验证了模型的实践可行性，并对安全风险隐患提出了改善措施和解决思路，保障了山区农村无信号交叉口的行车安全。

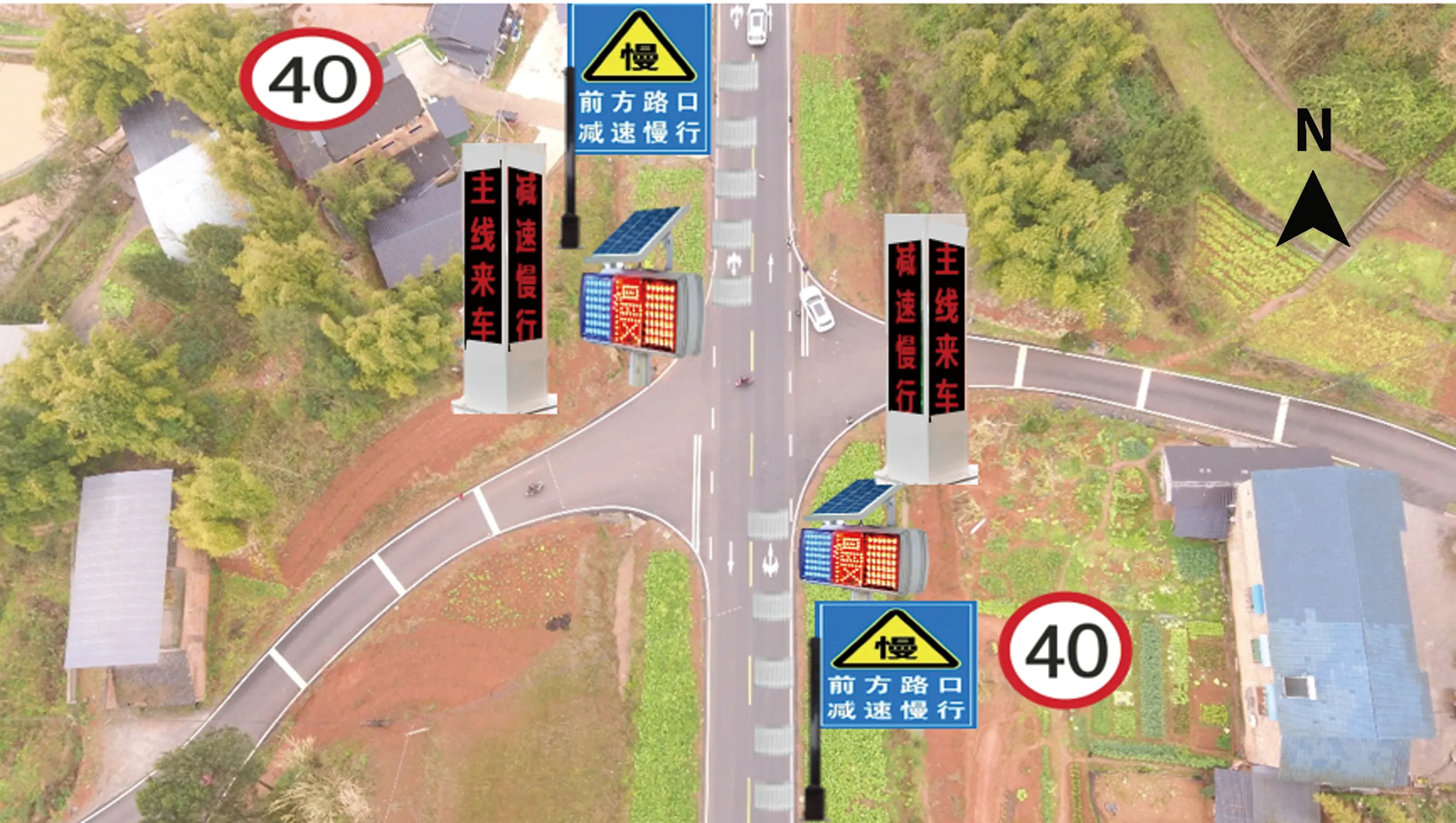
图6 十字交叉口综合处置效果图Fig.6 Effect diagram of comprehensive disposal at intersection