基于智能反射面辅助的无线供电通信网络鲁棒能效最大化算法

徐勇军 高正念 王茜竹 周继华 黄 东

①(重庆邮电大学通信与信息工程学院 重庆 400065)

②(重庆邮电大学移动通信重点实验室 重庆 400065)

③(航天新通科技有限公司 重庆 401332)

④(贵州大学现代制造技术教育部重点实验室 贵阳 550025)

1 引言

未来物联网为了实现万物智能互联需要部署大规模无线设备以感知周围环境信息，然而无线设备面临能量受限的问题[1]。为了解决这个问题，无线供电通信网络(Wireless-Powered Communication Network, WPCN)[2–4]被提出。WPCN的基本思想是在无线设备附近部署专用能量站，并让能量站按需给能量受限设备提供能量，而无线设备则利用收集的能量传输信息。

无线资源分配是实现WPCN能量调度、信息传输的关键技术，从而受到学术界、产业界的广泛关注。具体来说，文献[5]研究了单天线WPCN中的最大化最小速率资源分配问题。文献[6]通过联合优化能量收集时间和发射功率，提出了一种多用户加权和速率最大化资源分配算法。针对多天线WPCN，文献[7]通过联合优化能量波束、传输时间和功率使得系统和速率最大化。文献[8]考虑能量收集、传输时间和用户服务质量等约束，提出了一种系统能效最大化资源分配算法。考虑不完美信道状态信息，文献[9]研究了和速率最大化的鲁棒资源分配问题。上述网络性能容易受到障碍物阻挡的影响，导致性能下降。

智能反射面(Intelligent Reflecting Surface,IRS)作为一种低功耗、高能效的新兴技术受到广泛关注[10]。具体而言，IRS集成了大规模无源反射单元可以独立调节接收信号的相移和幅度，从而改变反射信号的传输方向。同时，IRS易灵活部署在建筑物表面、室内墙面和天花板等地方，有助于消除WPCN的覆盖盲区，增大网络连接性[11]。为了解决WPCN系统性能容易受到障碍物阻挡的问题，将IRS融入到现有的WPCN中是一种有效的解决方案。基于IRS辅助的WPCN，文献[12]通过联合优化传输时间和IRS无源波束成形矩阵使得和速率最大。文献[13]针对用户协作场景研究了加权和速率最大化资源分配问题。针对IRS辅助的多天线WPCN，文献[14]考虑用户能量收集、传输时间和发射功率约束，研究了系统和吞吐量最大化问题。

然而上述工作没有考虑能效优化问题，基于此，文献[15]针对IRS辅助的多用户无线通信网络，考虑最小速率约束、传输功率约束和反射相移约束，研究了系统能效最大化问题。该工作为研究IRS系统能效优化问题提供了有价值的指导，但其资源分配机制不能直接应用到WPCN网络。此外，上述工作忽略了信道不确定性的影响。因此，为了减少能量消耗同时提高传输速率和系统鲁棒性[16]，本文提出一种更贴近实际应用需求的高能量收集效率WPCN系统架构和鲁棒波束成形算法，主要贡献如下：

(1) 考虑系统能量消耗，基于有界信道不确定性，建立了一个联合优化能量波束、IRS相移、传输时间和发送功率的多变量耦合非线性资源分配问题。该问题是一个含参数摄动的非凸分式规划问题，很难直接求解。

(2) 为了求解该问题，利用最坏准则和S-Procedure方法将含参数摄动的鲁棒约束条件转化成确定性的约束；在此基础上，利用广义分式规划理论和变量替换方法将非凸问题转化成确定性凸优化问题。最后提出一种基于迭代的鲁棒能效资源分配算法。

(3) 仿真结果表明，本文算法具有较好的收敛性、能效和鲁棒性。

2 系统模型及问题描述

本文考虑1个IRS辅助的下行传输WPCN如图1所示，该网络可以缓解障碍物阻挡情况下能量收集效率低的问题。网络中含有1个M根天线的能量站，1个含N个反射单元的IRS，1个单天线的信息

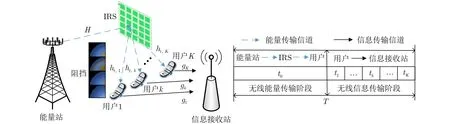
图1 IRS辅助多用户WPCN

其中， C1和C 2分别为用户能量收集和服务质量约束， C3 为 总传输时间约束，C 4为能量站发送功率约束， C5为反射相移约束。与现有工作类似[12–15]，设置每个反射单元的幅度为1是为了最大化反射效率，通过相移优化来改变信号传输方向。 C6为不确定性参数集合。由于目标函数和不确定性约束条件，问题式(7)是一个含不确定性参数扰动的多变量耦合分式规划问题，难以直接求解。

3 优化问题转换

3.1 不确定性问题转换

3.2 凸优化问题转换

问题式(20)是标准的凸半正定规划问题[13]，可利用CVX工具箱求解。由于在问题式(20)中松弛了Rank(V)=1的约束，意味着问题式(20)获得的最优解仅是问题式(19)的上界。因此利用高斯随机化方法构造V的唯一解[14]。

假设通过问题式(2 0)获得的解为V*，若Rank(V*)=1 ，则采用特征值分解得到v*；若Rank(V*)̸=1 ， 则 对V*进 行 特 征 值 分 解 为V*=UΛUH，其中，U∈CN×N和Λ∈CN×N分别为酉矩阵和对角矩阵。则次优解可以表示为v¯ =UΛ1/2r，其中r∈CN×1为r～CN(0,I)的圆对称高斯随机变量。因此问题式(19)的最优解为所有随机变量中使问题式(19)的目标函数最大的一个。因此，可设计如表1所示的基于迭代的鲁棒能效最大化算法。

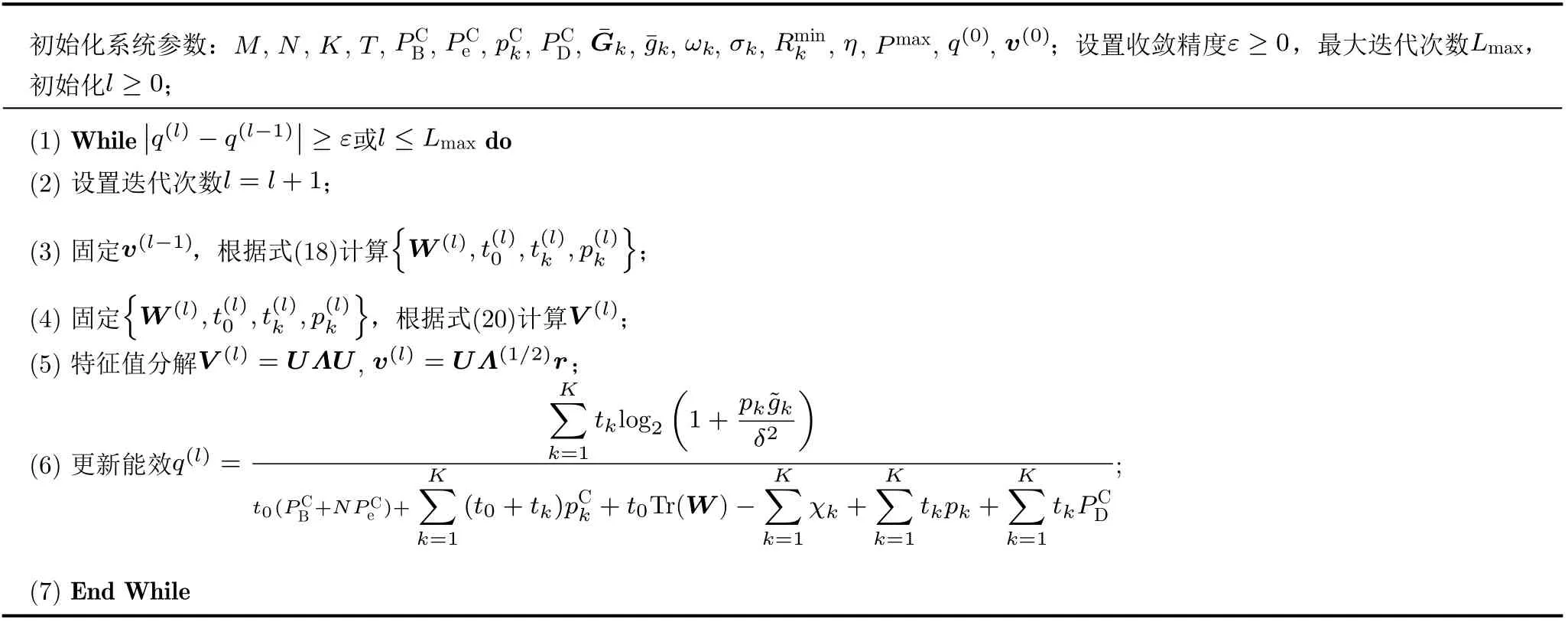
表1 基于迭代的鲁棒能效最大化算法

4 仿真结果与分析

图2给出了系统能效收敛图。从图2可看出，本文算法在经过几次迭代后达到收敛，说明所提算法具有较好的收敛性。且随着天线数M和反射单元数N的增加，系统能效增大。因为增加天线数量和反射单元数量均可增强能量传输效率，使得更多的能量信号被反射到用户处进行收集。一方面，减少了第1阶段的能量传输损耗；另一方面，增大了用户用于数据传输的发射功率可行域。

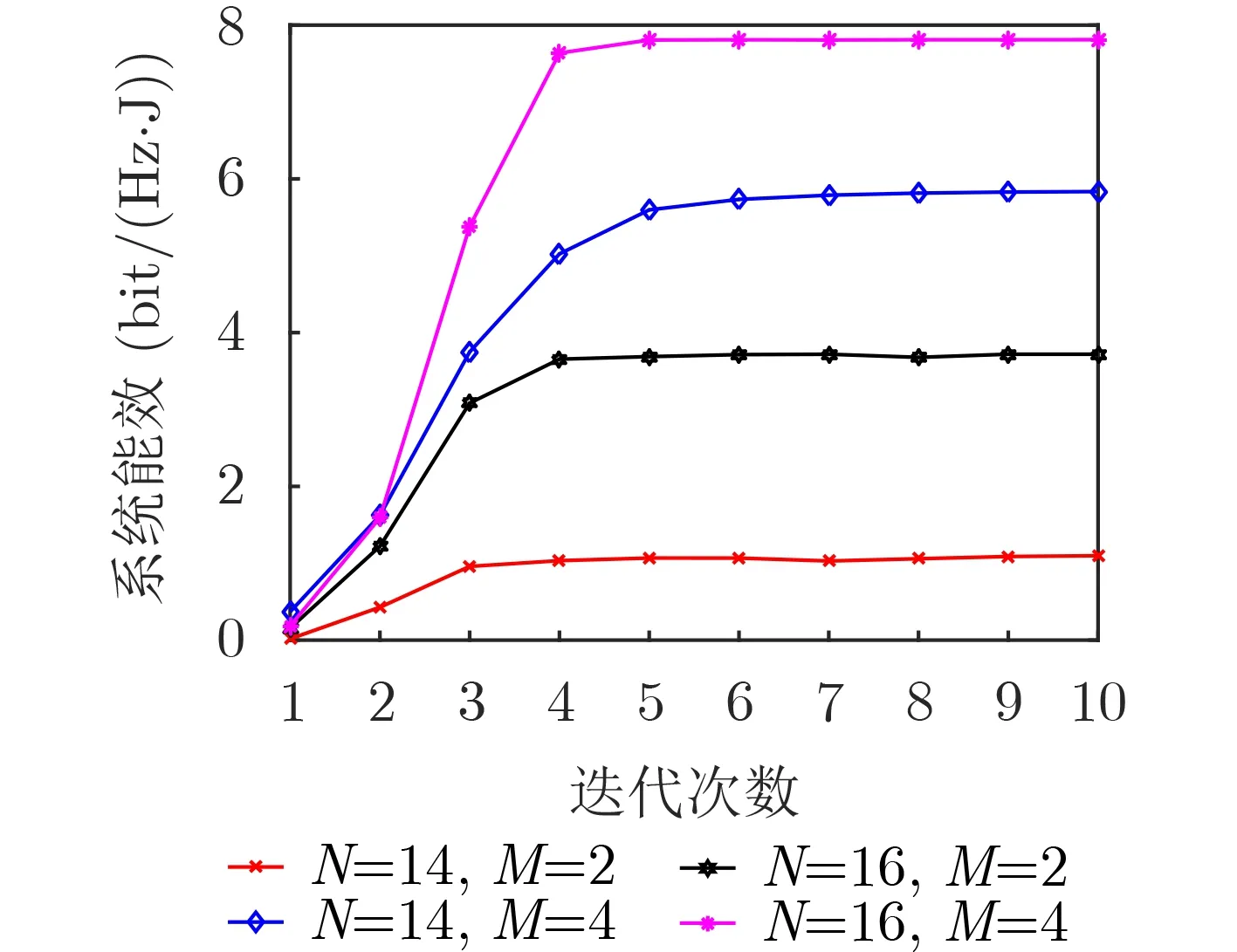
图2 系统能效收敛图

图3给出了系统能效与Pmax之间的关系。从图3可看出，随着Pmax增加，系统能效增加；随着用户数K增大，系统能效上升。因为增加Pmax可增加用户收集的能量，从而为第2阶段的数据速率提升提供有利条件，从而使得系统能效增大。此外，增加用户数量可以增加第1阶段的能量收集总量，且在第2阶段可以提升系统总吞吐量，进而带来系统能效的提升。

图3 系统能效与能量站最大发射功率在不同用户数下的关系

图4给出了不同算法系统能效与Pmax之间的关系。从图4可看出，随着Pmax增加，不同算法系统能效增加，其原因是Pmax增加意味着能量站可以发射更大功率的能量信号，用户可以在短时间内收集足够的能量供给第2阶段数据传输，使得系统总吞吐量提升，从而提升系统能效。但当Pmax增大到一定值时，吞吐量最大化算法的系统能效减小，因为该算法的能量消耗程度比速率增长快。此外，在相同Pmax取值下，本文算法有更高的系统能效。因为本文算法对能量收集约束和最小吞吐量约束均引入了鲁棒设计。

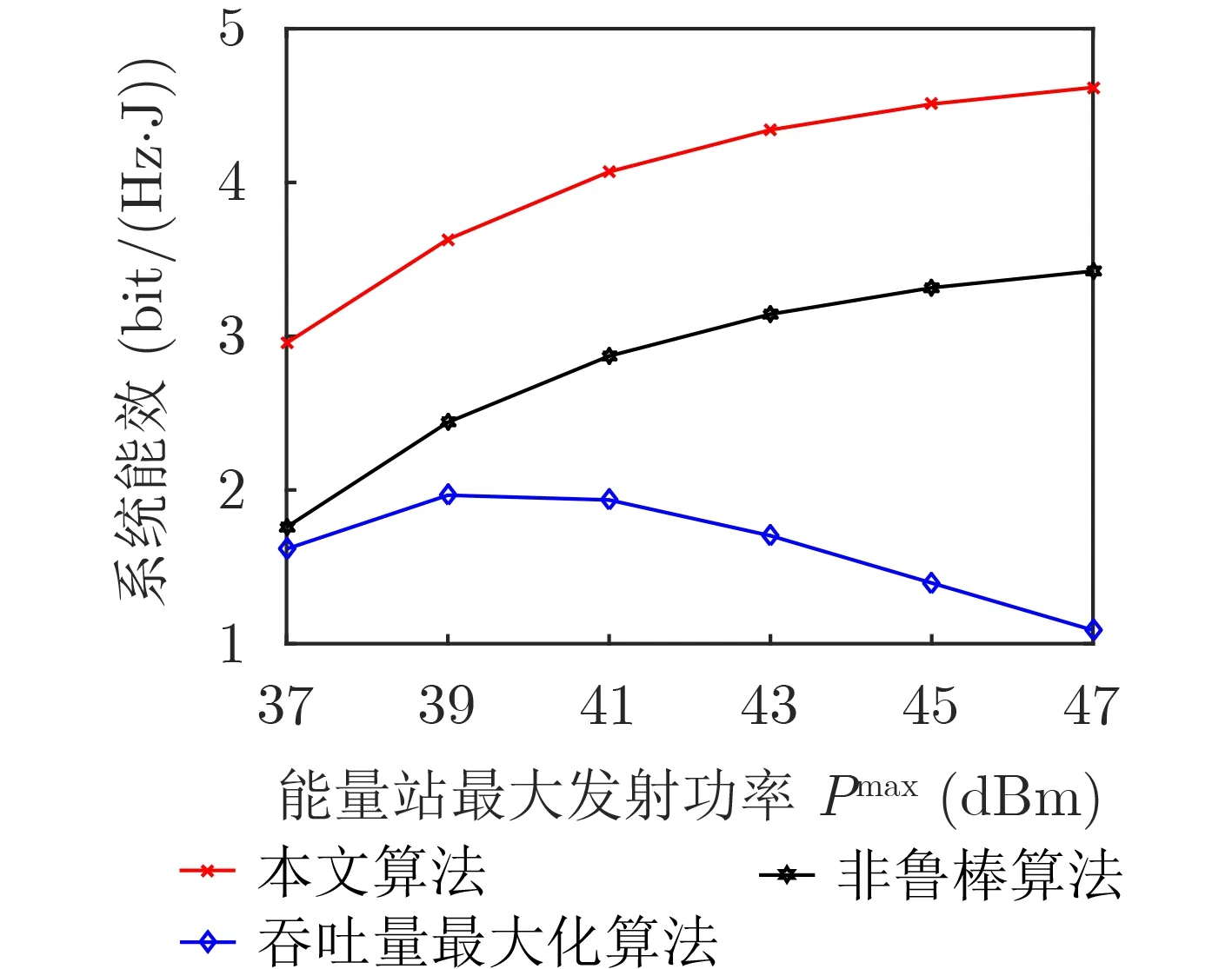
图4 系统能效与能量站最大发射功率在不同算法下的关系

图6给出了不同算法系统能效与信道不确定性之间的关系。从图6可看出，随着信道不确定性增加，不同算法系统能效减小；且本文算法系统能效高于其他算法。增加信道不确定性会导致信道环境变差，使得用户实际收集的能量和实际传输速率减小，从而使得系统能效降低。而本文算法提前考虑了信道不确定性的影响，对能量收集约束和最小吞吐量约束均进行了鲁棒设计，使得系统可以发射更大的功率来克服信道不确定性影响，从而缓解了信道不确定性对能效性能的影响。

图6 系统能效与信道不确定性在不同算法下的关系

图7给出了不同算法下中断概率与信道不确定性Δgk之间的关系。从图7可看出，随着信道不确定性增大，不同算法中断概率增加，且本文算法中断概率低于其他算法。一方面，信道不确定性Δgk增加，意味着信道估计值偏离实际值越大，对系统扰动增加，使得实际数据吞吐量小于最小吞吐量门限，因此中断概率增加。另一方面，在相同不确定性条件下，本文算法通过提前考虑系统的鲁棒性，使得用户发射功率大于其他算法，因此能够在一定范围内克服信道不确定性引起的中断。

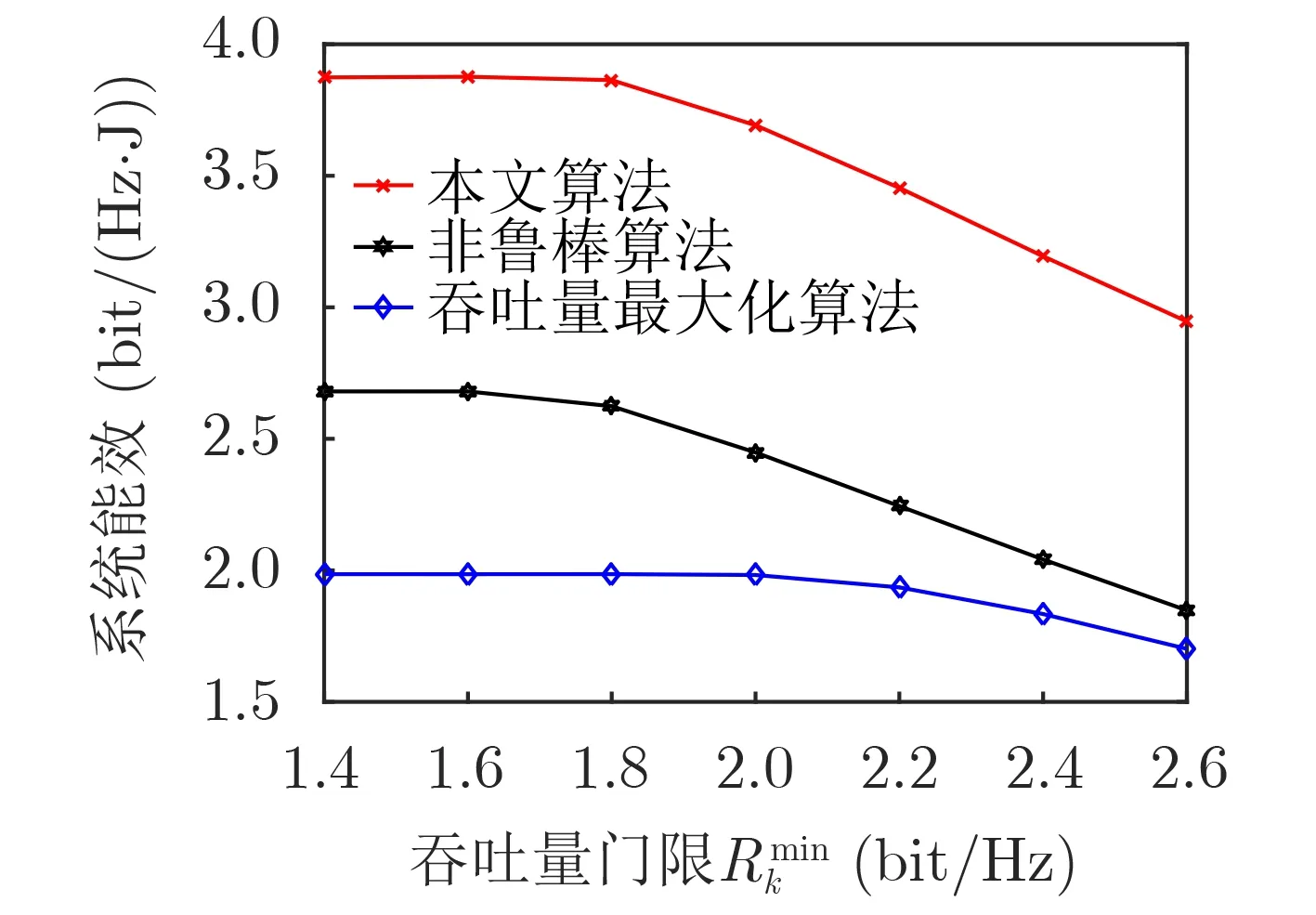
图5 系统能效与吞吐量门限在不同算法下的关系

图7 中断概率与信道不确定性在不同算法下的关系

5 结论

本文针对IRS辅助的WPCN鲁棒能效资源分配问题进行研究。考虑能量收集和用户服务质量约束，建立了一个多变量耦合的鲁棒能效最大化资源分配问题。利用最坏准则和S-Procedure方法将原问题转换为确定性问题；同时采用广义分式规划理论、交替优化和变量替换等方法将该问题转换为凸优化问题进行求解。仿真结果验证了本文算法具有较好的鲁棒性和能效。