考虑钢筋混凝土梁柱节点受力特征的钢筋锚固受力性能试验*

杨 红 刘清培 杨小乙

(1.重庆大学土木工程学院，重庆 400045；2.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400030)

0 引 言

在钢筋混凝土(RC)框架结构、框架-剪力墙结构中，节点是保持结构体系完整、可靠传递梁柱构件内力的关键部位。国内外震后调查、研究表明[1-2]，节点核心区可能先于梁、柱发生破坏，节点严重损伤可能导致结构产生明显侧移甚至局部倒塌。因此，钢筋混凝土梁柱节点的抗震性能、有限元模拟方法一直是国内外学术界关注的重要问题。

大量钢筋混凝土梁柱组合体试验结果表明[3-5]，随着梁纵筋在节点内的黏结滑移变形、节点区的非弹性剪切变形在试验后期逐渐增大，这两类节点非弹性变形对梁柱组合体受力性能的影响也越来越明显。其中，当贯穿节点的梁纵筋发生滑移后，梁端相对柱边缘会产生较大附加转动，梁柱组合体的耗能能力明显减小、刚度急剧下降，从而引起框架结构产生较大侧移；试验结果表明[4-7]，由节点内梁纵筋黏结滑移引起的梁附加挠度一般为梁柱组合体梁端总挠度的30%～50%。因此，正确描述梁纵筋在节点区的黏结滑移规律是节点有限元模型合理的关键之一。

但是，大部分梁柱组合体试验并未对梁纵筋黏结滑移变形进行专门测量。例如，赵雯桐对其收集的336个梁柱组合体试验进行了统计，其中对梁纵筋滑移变形进行测量并给出完整测量数据的试验很少，不足试件总数的10%，可见相关试验数据非常缺乏[8]。此外，在这些数量不多的梁柱组合体试验中，梁纵筋在节点区的黏结滑移一般采用图1a所示装置测量[7-8]，而采用图1a所示方法测得的梁纵筋滑移数据常存在误差，其误差主要来源于以下三个方面：1)由于梁柱组合体试验主要目的是研究节点剪切受力性能，因此试验破坏时节点区混凝土损伤非常严重、剪切变形显著(图1b)，而实际工程中的梁柱节点按照“强节点”设计后，在强烈地震作用下节点区混凝土一般不会损伤如此严重，即梁柱组合体试验的梁纵筋锚固受力环境一般非常差，是一种非常不利的受力情况，与工程常见的锚固环境不同；2)梁纵筋滑移变形的试验实测值包含一小段梁端纵筋(而不是节点内梁纵筋)的塑性伸长，会造成实测值偏大；3)梁端产生的弯曲裂缝有时正好位于测点和柱截面之间，导致滑移实测值偏大。

a—纵筋滑移测量装置[7]；b—试件BL-2节点损伤[4]。

考虑节点非弹性变形的早期有限元方法一般是通过在杆单元端部附加弹塑性转动弹簧，间接考虑节点区的梁纵筋滑移变形以及节点剪切变形的影响，例如Otani[9]、Birely等[10]、杨红等[11]。此类节点有限元模拟方法的优点是建模简便、计算量小，但无法有效模拟节点的局部反应。为更精确地模拟节点区的非弹性反应，细化的节点有限元模型逐渐被提出，如Yang等[4]、Elmorsi等[12]、Youssef等[13]、Shin等[14]建议的有限元模型。最具有代表性的是Lowes等[15]提出的“超级节点”单元模型，它由8个钢筋滑移分量模拟贯穿节点核心区梁、柱纵筋黏结退化，4个界面剪切分量模拟节点四周交界面损伤引起的剪力传递能力的下降，1个剪切板单元模拟节点核心区抗剪承载力和刚度的退化(图2a)；Mitra等[16]对“超级节点”单元模型进行了改进，并将梁柱节点单元模型(Beam-Column Joint Element)引入OpenSees结构分析软件[17]，得到了广泛应用。上述细化节点有限元模型计算量较大，优点是局限性小，通常考虑了多种变形机制，力学模型更合理。

a—“超级节点”单元模型[15]；b—节点内梁纵筋黏结应力分布[16]。

以上各节点有限元模型中，用于描述节点弹塑性剪切变形特征的模型化方法已有较多研究成果，一般可从节点核心区的传力机制出发，采用斜压杆模型[18-19]或拉压杆模型[20-21]计算节点的剪应力-剪应变骨架曲线，且经过与试验结果对比，已校核了这些方法的合理性[18-21]。

但是，描述梁纵筋在节点区黏结滑移规律的纵筋应力-滑移恢复力模型目前仍较为简化。例如，在附加弹塑性转动弹簧的有限元模型中，弯矩-当量转角恢复力模型是参考梁纵筋在节点内的黏结滑移规律，经简化、换算而得到；在“超级节点”中，Mitra等[16]建议的用于模拟节点区钢筋滑移的Bar-slip Material材料模型是以单根锚固钢筋的单调受拉试验数据为基础，对钢筋黏结应力分布进行简化后(图2b)得到的。这种描述节点内梁纵筋黏结滑移特征的简化恢复力模型未考虑一些重要因素(如轴压比、加载方式等，详见后文)的影响，其合理性、有效性仍有待研究。如赵雯桐等以多组RC梁柱组合体试件试验为依据，对OpenSees的“超级节点”单元模型的有效性进行了校准，结果表明：模拟节点内梁纵筋滑移分量的材料模型存在明显误差，当梁纵筋滑移量较大时，模拟的组合体整体滞回受力曲线与试验结果相比差异较明显[22]。

事实上，受多种因素影响，梁纵筋在节点内的黏结滑移规律明显比传统锚固滑移问题更加复杂。首先，随着节点区混凝土交叉剪切斜裂缝开展、延伸，节点区混凝土损伤逐渐加重，导致梁纵筋在节点区的黏结受力环境逐渐劣化。其次，柱轴压力可提高梁纵筋在节点内的锚固受力性能，它相当于对普通锚固钢筋试件施加侧向压力。第三，在节点核心区两侧的梁纵筋总是处于一侧受拉(强震下通常受拉屈服)、一侧受压的状态，从而使得梁纵筋与节点混凝土之间会形成较普通锚固更大的黏结应力和滑移。最后，梁纵筋的屈服渗透在拉压交替受力过程中不断发展，导致梁纵筋滑移加大。

综上所述，梁纵筋在节点内的应力-滑移本构模型一般是在传统单根钢筋锚固试验基础上建立的，单根锚固钢筋在单调受拉试验中的锚固受力环境单纯，与地震作用下贯穿节点区梁纵筋的复杂受力状态差别很大。经文献检索，很少有专门根据RC梁柱节点的受力规律对锚固钢筋的黏结性能、滑移变形进行试验的研究成果。本文基于梁纵筋在节点内的受力特征设计锚固钢筋循环拉压试验，测量钢筋的黏结滑移变形，基于应力-滑移试验结果，分析加载方式、轴压力、相对锚固长度、钢筋屈服强度、混凝土强度对钢筋黏结滑移规律的影响。论文研究的主要目的是论证基于单根锚固钢筋单调受拉试验建立节点内梁纵筋应力-滑移本构模型的做法存在明显误差，以便为后续研究制定合理的试验方案提供依据，并为模型改进提出建议。

1 试验概况

锚固钢筋的循环加载试验中重点考察相对锚固长度、轴压比、钢筋屈服强度、混凝土强度等因素的影响；通过与单调加载的试验结果对比，分析加载方式对锚固钢筋滑移变形的影响。

1.1 试件设计

设计制作了11个试件用于考察钢筋在混凝土中的锚固受力性能和钢筋应力-滑移关系，如表1所示。

表1 试件设计参数

在表1中，各试件通过参数设计重点考察相对锚固长度(Lc/ds，Lc为钢筋的锚固长度，ds为钢筋的直径)、轴压比(nt)、钢筋屈服强度(fy)、加载方式(拉-拉循环加载、拉-压循环加载等)等的影响。其中，轴压比nt根据试件施加的轴压力Nt，按照nt=Nt/(150Lcfc)计算，式中Lc和150 mm分别为试件锚固混凝土侧面的长度、宽度；fc为试件混凝土的轴心抗压强度，是根据混凝土的立方体抗压强度fcu150的实测结果，并按照我国现行GB 50010—2010《混凝土结构设计规范》[23]的条文规定，按fc=0.76fcu150计算所得。表1给出了各试件在试验当天的fcu150实测值，均为3个同时浇筑、同条件养护的立方体试块抗压强度的平均值。

GB 50010—2010[23]的第11.6.7条的规定，框架梁上部纵筋直径不宜大于矩形柱在该方向截面尺寸的1/20，即hc/ds≥20，其中hc为矩形柱在钢筋锚固方向的截面高度。考虑到实际结构的梁柱节点之中，在同一时刻，贯通布置的梁纵筋在节点左端、右端一般分别承担拉力、压力(或压力、拉力)，故梁筋在每一端的外力作用下对节点混凝土锚固长度的需求大致可等效为hc/2，即本文采用单侧加载时(如图3所示的单侧拉压受力)钢筋的锚固长度Lc大致与实际结构中贯穿梁柱节点区的梁纵筋的锚固长度hc的一半是相当的。因此，与hc/ds=20的梁柱节点相比，采用图3所示的单侧加载对钢筋进行试验时，钢筋的锚固长度Lc可近似取为10ds。故本文各试件的相对锚固长度(Lc/ds)最小值取10，Lc/ds=15, 20, 30则分别表示柱截面尺寸更大时梁纵筋在节点内的锚固受力情况。

对各试件进行了编号，其编号方式如下：以“试件LL-15-B5-N2”为例，“LL”表示加载方式(LL为拉-拉循环加载，LY为拉-压循环加载，DL为单调受拉加载，加载制度详见后文)，“15”为相对锚固长度Lc/ds的取值，“B5”表示钢筋的强度等级(B5为HRB500钢筋，B4为HRB400钢筋)，“N2”表示轴压力的相对大小(N2为轴压比等于0.2，N0为不施加轴压力)。

在表1中，混凝土强度fcu150均为各试件在试验当天的实测值，其结果皆为3个同时浇筑、同条件养护的立方体试块的抗压强度平均值。各试件的锚固钢筋来源于3根长度为9 m的母材，故对3根母材的钢筋强度(屈服强度fy或极限抗拉强度fu)分别进行了测量，且每根母材的锚固钢筋的fy或fu均为3个钢筋试件的单调受拉材性试验所得结果的平均值。

如图3所示，各试件的锚固钢筋直径ds均为16 mm，分别采用HRB400钢筋或HRB500钢筋(屈服强度fy和极限强度fu分别见表1)。钢筋外部用于锚固的混凝土截面尺寸均为150 mm×150 mm，各试件锚固混凝土的长度Lc等于表1中的Lc/ds乘以ds。

图3 试件尺寸

为体现梁柱节点的配筋特点，各试件混凝土内配置了2道直径为6 mm的HPB300箍筋，角部为4根直径6 mm的短钢筋以形成钢筋骨架，如图4所示。

a—配筋与模板；b—浇筑混凝土后。

1.2 加载方案与测量方法

各试件均采用如图5所示试验加载装置。该试验装置以3 cm厚钢板为底板，底板通过8根高强螺杆与基座相连。在底板之上，布置了左、右两个组合钢结构作为试件受力的反力架，组合钢结构通过螺杆与底板相连，通过移动两个组合钢结构的螺栓孔位置可调节反力架之间的距离，以适用于不同Lc(锚固长度)的试件。

a—示意图；b—加载现场。

各试件采用500 kN水平作动器对试件的锚固钢筋施加拉力(P+)、压力(P-)，通过拧紧螺栓施加竖向压力(Nt)。试件顶部依次布置了3 cm厚钢板、传感器、3 cm厚钢板，通过拧紧4个高强螺杆将轴压力Nt作用在试件外部混凝土的顶面。水平力P则通过“连接端头”(由两块钢板、4根高强螺杆连接成的整体，详见图5a)将试件的锚固钢筋和水平作动器连接起来，其中，作动器通过圆柱形的铁销与连接端头相连，试验中采取了侧面约束措施防止连接端头转动、侧移；钢筋穿过连接端头的孔洞，并通过专用锚夹具与连接端头相连。

研究结果表明[4,7-8,11]，在梁柱组合体试件的低周反复加载试验中，梁端截面上、下纵筋受拉时均会屈服，但受压时则均不会屈服。其中，负弯矩作用时由于梁端截面的下部混凝土为受压区，与纵筋共同受压，下部纵筋一般不会受压屈服；正弯矩作用时上部纵筋受压，由于下部纵筋的配筋面积总是明显更少，上部纵筋也不会受压屈服。总之，框架梁端部截面的上、下纵筋受压时的应力水平较小，一般明显低于屈服应力，在框架梁的典型配筋条件下(如底面、顶面的梁纵筋截面面积的比值为0.4～0.7)，梁纵筋受压的应力水平约为0.5fy左右。根据梁纵筋的这种受力特征，本文对锚固钢筋采用了如图6b所示的拉-压循环加载制度。

除个别试件的水平力P采用传统的单调受拉加载外，其他试件采用如图6所示的拉-压循环加载或拉-拉循环加载，以体现梁端部纵筋在梁柱组合体试件中的循环受力特点，并通过对比图6a与图6b所得的试验结果考察加载方式的影响。其中，拉-拉循环加载(图6a)时钢筋仅承受拉力，拉力卸载后不施加压力；拉-压循环加载(图6b)时钢筋承受拉力并在卸载后，反向施加压力，且按0.5fy控制压力值(受拉屈服后)，从而体现梁纵筋在节点内的循环拉、压的受力特点。

a—拉-拉循环；b—拉-压循环。

试验过程中，首先分三级施加预定的轴压力Nt，Nt在试验过程中保持恒定；然后开始水平力P的荷载控制阶段，如图6所示，即进行预加载阶段、屈服力(Py)阶段。其中，当钢筋受拉的应变实测值等于屈服应变εsy=fy/Es时定义为达到屈服位移sy。钢筋屈服之后即开始位移控制阶段，通过控制钢筋加载端位移等于nsy(n=2、3、4)的方法进行加载，每级循环两次。控制位移等于4sy的循环加载完成之后，按单调受拉方式加载直至钢筋拉断或被拔出锚固混凝土(滑移快速加大)，停止试验。本文采用上述力-位移混合加载制度，目的是与梁端加载的梁柱组合体试验的加载制度协调一致。

如图5所示，对锚固钢筋施加的拉力(P+)、压力(P-)，以及外部混凝土承受的竖向压力(Nt)均由力传感器测量；钢筋关键位置贴有应变片，用于力控制阶段确定sy，试件前端(加载端)的钢筋滑移变形(s)、尾端(自由端)的滑移变形(send)均由百分表测量(图5和图7)，且前端的滑移变形在钢筋屈服后用于控制位移加载。

a—尾端(自由端)；b—前端(加载端)。

试验中，将百分表的测头直接顶住钢筋自由端的尾部，测量钢筋尾端的滑移变形send(图7a)；在试件加载端一侧距离混凝土前端表面1.0 cm处将“丁”字形组合钢筋点焊在锚固钢筋上，通过“丁”字形钢筋引出两个测点，两测点对称布置，采用两个百分表分别测量两测点的滑移变形(图7b)，并取其平均值为前端的滑移变形(s)，以此消除连接端头有可能在水平方向产生微小变形对测量结果的干扰。钢筋前端采用夹具将钢筋夹住，以防止纵筋受压时弯曲(图7b)。

2 试验现象与破坏特征

各试件一般因钢筋被拉断或被拔出(或通滑)而停止试验，其中，Lc/ds=30的各试件由于钢筋在混凝土中的锚固长度较大，钢筋的黏结能力在试验后期仍未完全退化，皆是由于钢筋被拉断而结束试验。

图8为试验结束后剖开外部锚固混凝土，2个试件(Lc/ds=15)锚固界面的损伤状态。由于该试件以钢筋在锚固混凝土中被拔出而结束试验，仔细观察可以发现，外部混凝土的锚固界面已基本磨平，表明试件的机械锚固已基本失效，钢筋月牙斜横肋之间充满了形成机械锚固的混凝土齿被压碎后的粉末。

a—试件LL-15-B5-N2；b—试件LY-15-B5-N2。

图9给出了试验结束后部分试件(轴压比为0.2、拉-拉循环加载)的混凝土破损和开裂状态。图9表明，各试件一般在加载中后期出现外部混凝土开裂，试验后期加载端(或前端)一侧的锚固混凝土会形成局部圆锥形破损区，且破损区的部分混凝土呈碎块状随钢筋被拔出。其中，Lc/ds=30的试件LL-30-B5-N2以钢筋被拉断而结束试验，自由端(或尾端)钢筋没有滑移变形，且混凝土表面未见明显开裂；Lc/ds=20的试件LL-20-B5-N2则以钢筋在混凝土中通滑而结束试验，钢筋未拉断，钢筋自由端随荷载增加逐渐开始滑移，试块加载端的混凝土有明显开展的裂缝；Lc/ds=15的试件LL-15-B5-N2和Lc/ds=10的试件LL-10-B5-N2仍以钢筋在混凝土中被拔出(或通滑)而结束试验，钢筋自由端滑移变形更大，钢筋在混凝土中的通滑更早出现。

a—Lc/ds=10的试件；b—Lc/ds=15的试件；c—Lc/ds=20的试件；d—Lc/ds=30的试件。

以试件LL-15-B5-N2和LY-15-B5-N2为例(相对贯穿长度Lc/ds=15、HRB500钢筋、轴压比nt=0.2)，分别采用拉-拉循环加载、拉-压循环加载进行试验时，试件的破坏现象、损伤特征类似，均是以钢筋在混凝土中通滑而结束试验、钢筋未拉断，加载端混凝土的锥形破坏区域类似，其差别是拉-压循环加载试件的钢筋滑移变形相对更大。

3 试验结果及分析

根据锚固钢筋加载端的拉压力(P)的试验实测结果，可计算钢筋应力σ=P/As，式中As为钢筋的名义截面面积。将σ与对应时刻的加载端滑移变形(s)测量结果一一组合，即可得到加载端钢筋应力-滑移(σ-s)曲线试验结果。依据试验所得σ-s曲线，分析了加载方式、相对锚固长度、钢筋屈服强度、混凝土强度等对钢筋黏结滑移变形规律的影响。

3.1 加载端σ-s曲线

图10给出了各试件的锚固钢筋在加载端的应力-滑移(σ-s)曲线试验结果，限于百分表量程，本文图10之中未包含各试件试验末期的σ-s曲线下降段。

图10的试验结果表明，加载方式、轴压力、相对锚固长度对试件σ-s曲线的影响较明显，例如，钢筋首次受拉屈服对应的加载端滑移变形一般随Lc/ds或nt的增大而减小，加载方式(拉-压循环加载、拉-拉循环加载、单调受拉加载)、钢筋屈服强度等参数对加载端σ-s曲线的影响规律详见下文的对比分析。

a—试件LL-30-B5-N0；b—试件LL-30-B5-N2；c—试件LL-30-B4-N2；d—试件LL-20-B5-N2；e—试件LL-15-B4-N2；f—试件LL-15-B5-N2；g—试件DL-15-B5-N2；h—试件LY-15-B5-N2；i—试件LY-15-B4-N2; j—试件LL-10-B5-N2；k—试件DL-10-B5-N2。

3.2 自由端荷载-滑移曲线

图11给出了部分试件的水平荷载-自由端滑移变形曲线(P-send)，由于失效方式为钢筋拉断的各试件(Lc/ds=30的试件)没有自由端滑移变形的有效测量数据，故图11中未列出。

⑤见《化雨春风六十年（华南人民文学艺术学院校史）》，北京：中国文联出版社，2007年12月，第223页。

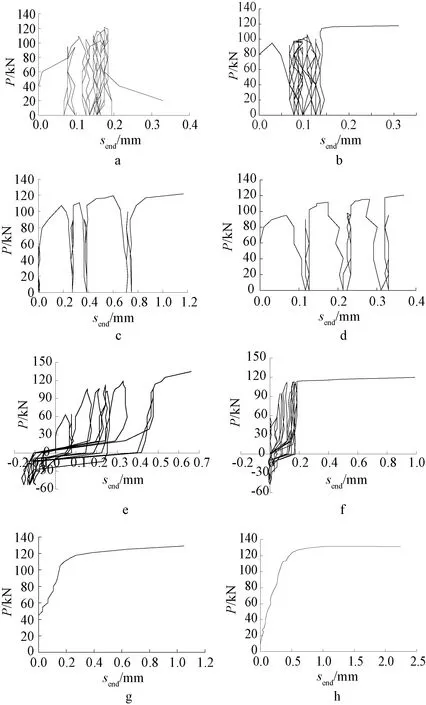
a—试件LL-20-B5-N2；b—试件LL-15-B4-N2；c—试件LL-15-B5-N2；d—试件LL-10-B5-N2；e—试件LY-15-B5-N2；f—试件LY-15-B4-N2；g—试件DL-15-B5-N2；h—试件DL-10-B5-N2。

试验结果表明，对于失效方式为钢筋被拔出的各试件，自由端的滑移变形一般在1.0 mm之内，明显小于加载端测得的滑移变形，且Lc/ds越小试件自由端滑移通常更大；循环加载(拉-压循环加载、拉-拉循环加载)下试件的P-send滞回曲线缺乏规律，自由端滑移并非本文的研究范围，此处不再赘述。

3.3 加载方式对加载端σ-s曲线的影响

以4个对比组，即试件LL-15-B5-N2和LY-15-B5-N2、试件LL-15-B4-N2和LY-15-B4-N2、试件LL-15-B5-N2和DL-15-B5-N2、试件LL-10-B5-N2和DL-10-B5-N2为依据分析加载方式的影响，每一对比组的2个试件仅加载方式不同(即Lc/ds、nt和fy均相同，仅混凝土强度略有差异)。

各试件实测的加载端σ-s曲线如图10所示，4个对比组的σ-s曲线见图12。

a—LL-15-B5-N2和LY-15-B5-N2；b—LL-15-B4-N2和LY-15-B4-N2；c—LL-15-B5-N2和DL-15-B5-N2；d—LL-10-B5-N2和DL-10-B5-N2。

根据试件LL-15-B5-N2和LY-15-B5-N2、试件LL-15-B4-N2和LY-15-B4-N2可分析拉-压循环加载、拉-拉循环加载对锚固钢筋σ-s曲线的影响。

在图12a中，试件LL-15-B5-N2和LY-15-B5-N2均以钢筋被拔出、钢筋在混凝土中通滑而结束试验。在试验前期，两试件的钢筋滑移变形有一些差异，例如，锚固钢筋首次受拉屈服时，试件LL-15-B5-N2和LY-15-B5-N2加载端的滑移变形分别为1.398 mm、1.546 mm；但是在试验后期，两试件的钢筋滑移变形差别较明显，其中试件LY-15-B5-N2由于承受拉-压循环加载，导致其黏结性能退化更快，滑移变形相对更大。因此，两试件的试验结果对比表明：拉-压循环加载会使试件LY-15-B5-N2的钢筋滑移变形更大，虽然对钢筋屈服时的滑移变形影响相对更小，但拉-压循环加载导致试件LY-15-B5-N2的后期滑移变形明显加大；而试件LL-15-B5-N2不但钢筋受拉屈服时滑移变形相对更小，且试验后期由于黏结性能退化更慢(未反向受压)，滑移变形相对更小。

在图12b中，试件LL-15-B4-N2和LY-15-B4-N2均以钢筋在混凝土中通滑而结束试验，其σ-s滞回曲线的外包线接近。两试件在试验前期(如钢筋受拉屈服时)的滑移变形较为接近，例如，试件LL-15-B4-N2和LY-15-B4-N2锚固钢筋首次受拉屈服时加载端的滑移变形分别为0.694 mm、0.774 mm；在试验后期，两试件的钢筋滑移变形、外包线均较为接近。因此，对比试验结果表明，试件LY-15-B4-N2承受拉-压循环加载，钢筋受拉屈服时的滑移变形比LL-15-B4-N2稍大；此外，由于试件LL-15-B4-N2和 LY-15-B4-N2为HRB400钢筋，试件LL-15-B5-N2和LY-15-B5-N2为HRB500钢筋，两个HRB400钢筋的试件屈服强度fy更低，根据GB 50010—2010[23]的基本锚固长度的计算式进行判断，试件的fy更低时钢筋的锚固性能从理论上来说相对更好(Lc/ds均为15)，这在一定程度上使得即使到了试验后期，拉-压循环加载对HRB400钢筋的滑移变形的影响相对而言仍不显著(相对HRB500钢筋而言)。

在以上对比分析过程中应注意，试件LL-15-B5-N2和LY-15-B5-N2、试件LL-15-B4-N2和LY-15-B4-N2的混凝土强度不同，其中，承受拉-压循环加载的试件LY-15-B5-N2和LY-15-B4-N2混凝土强度相对更大。考虑这一因素的影响，在图12a和12b中，若试件LY-15-B5-N2和LY-15-B4-N2的混凝土强度降低至fcu150=34 MPa，则这两个试件的钢筋滑移变形预计将进一步加大(随着混凝土强度减小，钢筋的锚固性能会相应降低)，因此，拉-压循环加载对滑移变形的增大影响也将相应更明显。

在图12c中，试件LL-15-B5-N2和DL-15-B5-N2均以钢筋在混凝土中通滑而结束试验，试件LL-15-B5-N2的σ-s滞回曲线的外包线与试件DL-15-B5-N2单调受拉的σ-s曲线接近。但锚固钢筋首次受拉屈服时，试件LL-15-B5-N2和DL-15-B5-N2加载端的滑移变形分别为1.445 mm、0.668 mm，即循环加载的试件LL-15-B5-N2的滑移变形明显更大。可见，与单调受拉加载相比，循环加载使钢筋与混凝土之间的黏结性能更容易退化，并导致钢筋滑移量增大。

在图12d中，试件LL-10-B5-N2和DL-10-B5-N2均以钢筋在混凝土中通滑而结束试验，两试件外包线接近，但锚固钢筋首次受拉屈服时加载端的滑移变形分别为1.495 mm、1.210 mm，差异相对更小(与试件LL-15-B5-N2和DL-15-B5-N2的差异相比较而言)，这与试件LL-10-B5-N2和DL-10-B5-N2的相对锚固长度(Lc/ds=10)更小(相对于前述两个Lc/ds=15的试件而言)，黏结性能退化更快有关。

综上所述，与单调受拉相比，拉-拉循环加载会使锚固钢筋的黏结性能更容易退化，并导致钢筋的滑移变形加大；与拉-拉循环加载相比，拉-压循环加载将进一步加快钢筋黏结性能退化，锚固钢筋的后期滑移变形也将相应加大。

因此，“超级节点”单元模型[16]和OpenSees软件[17]等基于锚固钢筋的单调受拉试验数据建立梁纵筋的σ-s材料模型，并将其用于细化节点有限元模型之中，这种简化做法将明显低估节点区梁纵筋在反复受力过程中的滑移变形，由此可能造成节点区的剪切变形偏大，或(和)梁、柱端部塑性铰区塑性变形的有限元计算结果偏大。

3.4 相对锚固长度、轴压力对加载端σ-s曲线的影响

试件LL-20-B5-N2、LL-15-B5-N2和LL-10-B5-N2仅相对锚固长度Lc/ds不同(分别等于20、15、10，混凝土强度差异很小，轴压力和钢筋屈服强度相同)，3个试件均以钢筋被拔出、钢筋在混凝土中通滑而结束试验，其加载端σ-s曲线如图10所示，其σ-s曲线对比见图13a。

a—LL-20-B5-N2、LL-15-B5-N2和LL-10-B5-N2；b—LL-30-B5-N0和LL-30-B5-N2。

图13a表明，3个试件在试验后期(特别是接近通滑状态时)钢筋的滑移变形接近，但钢筋受拉屈服时以及加载端位移为1sy～2sy时滑移变形存在明显差别，例如，试件LL-20-B5-N2、LL-15-B5-N2和LL-10-B5-N2的锚固钢筋首次受拉屈服时加载端的滑移变形分别为0.620，1.398，1.495 mm。可见，Lc/ds越大，通滑之前钢筋的黏结性能越好，钢筋受拉屈服时的滑移测量值越小，但黏结性能失效后钢筋的滑移均很明显，滑移变形量差异不明显。

在图13b所示的σ-s曲线对比中，试件LL-30-B5-N0未施加轴压力，与钢筋锚固试验的传统做法相同；试件LL-30-B5-N2的轴压比nt为0.2。两试件仅轴压力不同，相对锚固长度Lc/ds和钢筋屈服强度fy相同，混凝土强度差异很小(fcu150分别为27.4 MPa、26.6 MPa)。试件LL-30-B5-N0和LL-30-B5-N2均以钢筋被拉断而结束试验，其σ-s曲线如图10所示。

图13b表明，试件LL-30-B5-N0和LL-30-B5-N2在试验前期的钢筋滑移变形很接近，例如，锚固钢筋首次受拉屈服时加载端的滑移变形分别为0.355 mm、0.347 mm。但在加载后期，钢筋的滑移变形存在明显差别，施加了轴压力的试件LL-30-B5-N2的滑移变形明显更小(卸载后的残余变形也明显更小)。可见，轴压力有利于提高锚固钢筋的黏结性能、减小黏结滑移变形。

因此，“超级节点”单元模型[16]和OpenSees软件[17]等基于锚固钢筋的单调受拉试验数据建立的梁纵筋σ-s材料模型不考虑轴压力的影响，难以合理模拟节点内梁纵筋在强烈地震作用下的滑移变形，这种简化做法将在一定程度上高估节点区梁纵筋在反复受力过程中的滑移变形，并进一步造成节点区的剪切变形偏小，或(和)梁、柱端部塑性铰区塑性变形的有限元计算结果偏小。

由于本文试验数量偏少，有待进一步完成数量较大的系列试验才能建立修正纵筋σ-s材料模型从而合理考虑循环加载、轴压力的影响，以更准确地体现节点内梁纵筋的受力特征。

3.5 钢筋屈服强度、混凝土强度对σ-s曲线的影响

在图14a的σ-s曲线对比中，试件LL-15-B4-N2、LL-15-B5-N2仅钢筋屈服强度不同，相对锚固长度Lc/ds、轴压力nt、混凝土强度fcu150和加载方式均相同，两试件均以钢筋被拔出、钢筋在混凝土中通滑而结束试验，其加载端σ-s曲线如图10所示。

a—LL-15-B4-N2和LL-15-B5-N2；b—LL-30-B5-N2和LL-30-B4-N2。

图14a表明，由于试件LL-15-B5-N2钢筋屈服强度更高，其滑移变形在试验前期、中期均相对更大，例如，试件LL-15-B4-N2、LL-15-B5-N2的锚固钢筋首次受拉屈服时加载端的滑移变形分别为0.694 mm、1.398 mm，但锚固失效后钢筋的滑移均很明显，滑移变形量差异不明显。

在图14b所示的σ-s曲线对比中，试件LL-30-B5-N2和LL-30-B4-N2除钢筋屈服强度fy不同外，混凝土强度的差异也较明显(相对锚固长度Lc/ds、轴压力nt和加载方式均相同)，两试件相对锚固长度较大(Lc/ds=30)，均以钢筋被拉断而结束试验。

图14b表明，试件LL-30-B4-N2的试验结果与其他各循环加载试件的σ-s曲线存在明显差别，其σ-s滞回曲线卸载后的滑移变形总是明显大于上一循环，即滑移变形具有一定的发散特征，分析后本文认为其与试件的制作缺陷、夹具未充分紧固导致的试验误差有关，因此难以根据据试件LL-30-B5-N2和LL-30-B4-N2的对比结果有效鉴别混凝土强度的影响。

考虑到试验前期滑移变形小时试验误差很小，以下仅将试件LL-30-B5-N2和LL-30-B4-N2的锚固钢筋首次受拉屈服时的滑移变形进行比较。试件LL-30-B5-N2和LL-30-B4-N2的锚固钢筋首次受拉屈服时加载端的滑移变形分别为0.347 mm、0.197 mm，与试件LL-30-B4-N2混凝土强度更高、钢筋锚固性能理应更好相符，但其中还掺杂了钢筋fy不同的影响，难以准确判断。关于混凝土强度对钢筋黏结性能的影响规律已有较多研究成果[24-26]可供参考，本文不再对此问题专门分析。

4 结 论

通过锚固钢筋的循环拉压试验，对钢筋应力-滑移滞回曲线的实测结果进行分析，得到以下结论：

1)试验结果表明，与单调受拉相比，拉-拉循环加载会使锚固钢筋的滑移变形加大，拉-压循环加载将进一步加大锚固钢筋的滑移变形。

2)轴压力有利于提高锚固钢筋的黏结性能、减小黏结滑移变形；增加钢筋的相对锚固长度，钢筋首次受拉屈服时的滑移变形将减小。

3)基于锚固钢筋的单调受拉试验数据建立的钢筋应力-滑移材料模型未考虑轴压力、加载方式的影响，难以合理模拟节点内梁纵筋在强烈地震作用下的滑移变形。

4)在钢筋混凝土梁柱节点的有限元模型中，建议对节点内梁纵筋的应力-滑移材料模型进行改进，除考虑轴压力的有利影响外，还应考虑钢筋反复拉压对滑移变形的不利影响。