多普勒差分干涉仪干涉图畸变对相位反演精度影响分析
周冠,李立波,傅頔,张亚飞,冯玉涛,刘长海
(1 中国科学院西安光学精密机械研究所光谱成像技术重点实验室,西安 710119)
(2 中国科学院大学,北京 100049)
(3 中国人民解放军63768 部队,西安 710200)
0 引言
中高层大气风场信息对研究上下层大气和能量的耦合、保障航天器太空活动的顺利开展以及进行中长期的气象预测至关重要[1-2]。多普勒差分(Doppler Asymmetric Spatial Heterodyne,DASH)干涉仪是一种新兴的被动式风场探测技术,相比迈克尔逊干涉仪风场探测技术,结构简单不含动镜组件、光通量更大且可对多谱线同时测量,适合搭载于卫星平台进行中高层大气风场测量[3-5]。基于DASH 干涉技术的全球高分辨率热层成像迈克尔逊干涉仪(Michelson Interferometer for Global High-resolution Thermospheric Imaging,MIGHTI)已搭载在电离层连接(Ionospheric Connection,ICON)卫星平台于2019年10月发射并开始运行[6]。
DASH 干涉仪基于对干涉图相位的精准反演探测大气气辉辐射谱线的多普勒频移,从而实现对大气风速的测量,而要满足实用的测风需求(<10 m/s),DASH 干涉仪探测多普勒频移的精度需要达到1/3×10-7波长级别,对应干涉图中5~10 mrad 的相位变化[4-5]。而对于干涉仪来说,光学元件和结构组件的加工和装配误差、光学系统的像差会造成干涉图像的畸变,导致干涉条纹变形,改变了条纹相位的像元分布,在相位反演过程中引入反演误差影响风速测量[7-8]。
为了减小干涉图畸变对相位反演的影响,ENGLERT C R 等[7]将相位畸变解析分为频率相关项和频率无关项,分别利用单色光源干涉图求解干涉图相位失真函数及在光谱域校正函数的卷积两种方法,实现了对多普勒差分干涉仪相位畸变的测量与纠正,并通过近紫外太阳光谱在空间外差干涉仪上的实验得到验证。HARLANDER J M 等[8]对宽视场空间外差干涉仪图像缺陷校正的研究中,针对干涉图像的畸变提出了一种通过标定相位误差项修正干涉图包络函数的算法,并利用汞灯546.1 nm 处谱线的干涉条纹进行实验验证,结果表明该算法可以有效修正干涉图上的条纹弯曲现象。目前针对DASH 干涉图畸变的研究,并未分析干涉图畸变对多普勒相位反演精度的影响,缺少多普勒差分干涉仪设计、加工、装调指标的定量理论依据。
本文基于布朗畸变模型,仿真分析了条纹弯曲、局部弯曲、倾斜、空间频率变化四种干涉图畸变分别对相位反演误差的影响。仿真发现等量畸变条件下干涉图局部弯曲产生的相位误差最大,对此进一步验证局部弯曲对于不同条纹频率系统的影响及不同弯曲区域、弯曲位置对相位反演的影响。并对含畸变干涉图多行像元合并过程的相位不确定度进行仿真计算。
1 多普勒差分干涉仪干涉图畸变分析
DASH 干涉仪的基本结构如图1所示,与迈克尔逊干涉仪相似,只是两臂的平面反射镜替换为以Littrow 角倾斜的固定光栅,而非对称偏置量Δd的加入增大了光程差,提高了相位灵敏度。入射光经前置光学系统准直进入干涉仪,被分束器分送至两条光臂,两臂的光各自经光栅的衍射作用返回,在空间中相遇形成斐索干涉条纹[5]。DASH 干涉图测量所得干涉条纹可以表达为[9-12]
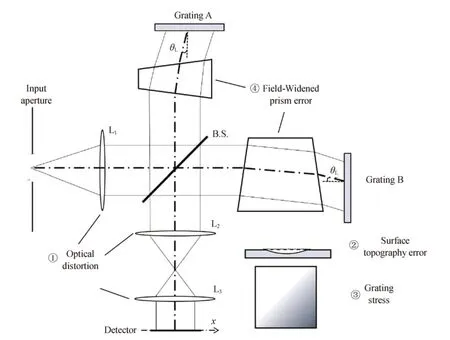
图1 多普勒差分干涉仪干涉图畸变来源Fig.1 Sources of DASH’s distortion

式中,x表示像素位置,σ和σL分别表示入射光波数及光栅Littrow 波数,B(σ)是入射谱密度,θL表示光栅倾角,4(σ-σL)tanθL是外差条纹频率,4πσΔd是干涉图初始相位。
目前DASH 干涉仪进行相位反演主要用基于傅里叶变换的方法,对干涉图经过预处理和风速反演两大流程得到相位的像元分布。预处理包含暗电平去除、平场校正、探测器效应校正、冲击噪声校正、基线去除及切趾[13]。对预处理后的干涉图进行傅里叶变换、单线提取、傅里叶逆变换、相位计算及相位修正操作后最终得到总相位值ϕ(x)[5,14]为

受畸变影响实际采样位置并非线性,以二阶径向畸变为例[15],即

式中,k1、k2为径向畸变系数,则含畸变相位(x)可表示为

多普勒差分干涉仪因畸变引起的系统相位误差ϕerror即为含畸变仪器测定目标风场时得到的相位值与理想仪器相位值ϕ(x)的差,即

式中,(x)为含畸变仪器测定的相位值,为含畸变仪器零风相位,ϕv(x)为理想仪器测定的相位值,ϕ0(x)为理想仪器零风相位。将式(2)和式(4)带入式(5)整理得

而入射波数σ受多普勒效应影响,与光源波数σ0及风速相关[16],即

由此可见多普勒差分干涉仪因畸变引起的系统相位误差ϕerror受目标风速、畸变程度及畸变类型影响。
干涉图畸变在图像中主要表现为条纹弯曲、条纹局部弯曲、条纹倾斜以及条纹空间频率变化,四种干涉图畸变如图2所示,其中条纹弯曲主要由成像光学系统的像差造成,而另外三种干涉图畸变主要由光学元件的加工和装配误差造成。光栅局部面型缺陷及装调应力使得光栅衍射波面并非理想平面,干涉得到的斐索条纹产生与光栅缺陷位置对应的局部弯曲;光栅装调时光栅沿主光轴的小角度旋转和沿垂直主截面方向的旋转及探测器沿主光轴的旋转都会使干涉条纹产生倾斜;干涉仪阔视场棱镜的旋转使得光程差随探测器采样位置非线性变化,引起干涉图上的条纹空间频率随采样位置改变。

图2 添加不同畸变的氧原子红线(630.0 nm)仿真干涉图Fig.2 The simulated red oxygen emission line(630.0 nm)interferogram with different distortion
2 干涉图畸变仿真
对于多普勒差分干涉仪,四种干涉图畸变在图像中的表现形式和各自引入的相位附加项有所不同,因此对相位反演的影响也有所不同。为了分别验证这四种畸变各自对相位反演的影响,需要对理想正演干涉图依照来源添加不同程度干涉图畸变,对比理想干涉图与含畸变干涉图反演多普勒相位时的差异,得到相位反演过程中不同干涉图畸变引起的系统误差。
成像系统畸变像差引起的条纹弯曲可以使用布朗畸变模型(Brown's distortion model)描述[16],即

式中,rd和ru分别为畸变后和畸变前像点距视场中心距离,k1、k2表示径向畸变系数。对于单参数布朗畸变模型,k1为负值表示桶形畸变,k1为正值表示枕形畸变。得到添加畸变后像素点坐标,对正演干涉图像素点阵进行三次样条插值,获得包含成像系统畸变的正演干涉图。连续改变参数值k1可得含不同畸变大小的单参数布朗畸变正演干涉图。
干涉图局部弯曲选取原始正演干涉图局部区域的图像,对该区域原像素坐标数值沿垂直条纹方向添加弯曲偏移量,令弯曲偏移量在图像中点处取最大,图像边缘处取零,得到添加弯曲的像素点坐标后,对该区域的正演干涉图像素点阵进行插值,最后将弯曲区域图像与原图像拼接,得到添加局部弯曲的正演干涉图。连续改变弯曲区域最大偏移量值可得含不同局部弯曲程度的正演干涉图。以弯曲偏移量随光程差成二次函数为例,含畸变干涉图坐标可表示为

式中,X为畸变后像素点坐标,xu为无畸变像素点坐标,kc1、kc2为局部弯曲畸变系数,改变kc1、kc2大小可以调整弯曲量大小、位置和方向。
条纹空间频率变化可对整幅原始正演干涉图像素坐标沿垂直条纹方向添加偏移量,令偏移量在图像右侧边缘视场取最大值,左侧边缘视场取零,干涉图中心偏移量随采样位置线性变化,得到像素点坐标后对正演干涉图像素点阵进行插值,获得添加条纹空间频率变化的正演干涉图。含畸变干涉图坐标可表示为

式中,ks为空间频率变化畸变系数,连续改变ks值获得包含不同偏移量的干涉图。
条纹倾斜只需要对原始正演干涉图绕采样中心旋转即可获得添加条纹倾斜的正演干涉图。连续改变图像旋转角度可获得含不同条纹斜角的正演干涉图。多普勒差分干涉仪仿真参数及干涉图畸变仿真参数见表1~2。

表1 多普勒差分干涉仪系统仿真参数Table 1 DASH simulation parameters

表2 干涉图畸变仿真参数Table 2 Interferogram distortion parameters
3 干涉图畸变对相位反演精度影响
为了验证各种干涉图畸变对相位反演的影响,以氧原子红线(630 nm)及氧原子绿线(557.7 nm)正演仿真干涉图为例,通过第2 节中计算畸变图像坐标后,对含畸变像素点阵进行三次样条差值,得到四种常见畸变。再选取干涉图中畸变最大的单行干涉图,通过HARLANDER J M 等采取的经典相位反演算法[10],对比理想干涉图与含畸变干涉图反演多普勒相位时的差值。
3.1 干涉图畸变种类对相位反演的影响
为了解干涉图畸变对不同目标风场观测状态下的精度影响,通过仿真目标风场0~100 m/s 的正演仿真观测图,添加四种不同大小的畸变,其中局部弯曲选取干涉图中心视场300×300 像元区域的图像,通过与理想干涉图对比计算反演多普勒相位时产生的系统误差。
四种类型的干涉图畸变在不同风速和不同畸变大小的情况下对氧原子红线和氧原子绿线的仿真结果如图3~4 所示。
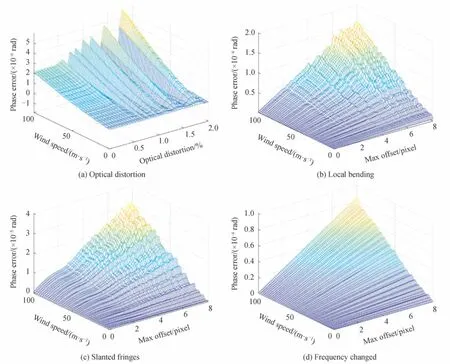
图3 不同干涉图畸变对氧原子红线(630.0 nm)多普勒相位反演的影响Fig.3 The Influence of different interferogram distortion on the phase retrieval of the red oxygen emission line(630.0 nm)


图4 不同干涉图畸变对氧原子绿线(557.7 nm)多普勒相位反演的影响Fig.4 The Influence of different interferogram distortion on the phase retrieval of the green oxygen emission line(557.7 nm)
对比氧原子红线和氧原子绿线的仿真结果可以看出,四种畸变中局部弯曲、条纹倾斜、条纹空间频率变化三种畸变带来的误差变化趋势一致,相位误差随着畸变程度和目标风速都成正比例关系。而畸变像差带来的条纹弯曲与其他三种畸变趋势不同,相位误差随着畸变程度呈现波动增大的特点,与目标风速的关系和其他三种畸变趋势一致,都呈现正比例增加的特点。对比四种畸变的影响程度可以看出,等量畸变大小和目标风速条件下,局部弯曲带来的相位误差最大,对氧原子红线(630.0 nm)多普勒源100 m/s 风速误差达到0.15 mrad 以上,即弯曲量每增加一个像元,系统误差增加0.113‰。而条纹弯曲、条纹频率变化、条纹倾斜带来的相位误差要小一两个数量级。对比氧原子红线和氧原子绿线结果发现,等量局部弯曲会对氧原子红线带来更大的多普勒相位误差。
3.2 干涉图局部弯曲对相位反演的影响
为验证3.1 节中等量局部弯曲会对氧原子红线带来更大多普勒相位误差的结论,进一步仿真了干涉图局部弯曲对不同条纹频率系统多普勒相位误差的影响,其中条纹频率正比于入射光波长与Littrow 波长的差值。通过仿真视场条纹频率1.3~2.7 mm-1目标风场100 m/s 的四个不同多普勒差分干涉仪正演干涉图,对所得正演干涉图依照第2 节局部弯曲方式添加不同大小的畸变,对比其与理想干涉图反演相位的差值,仿真结果如图5所示。
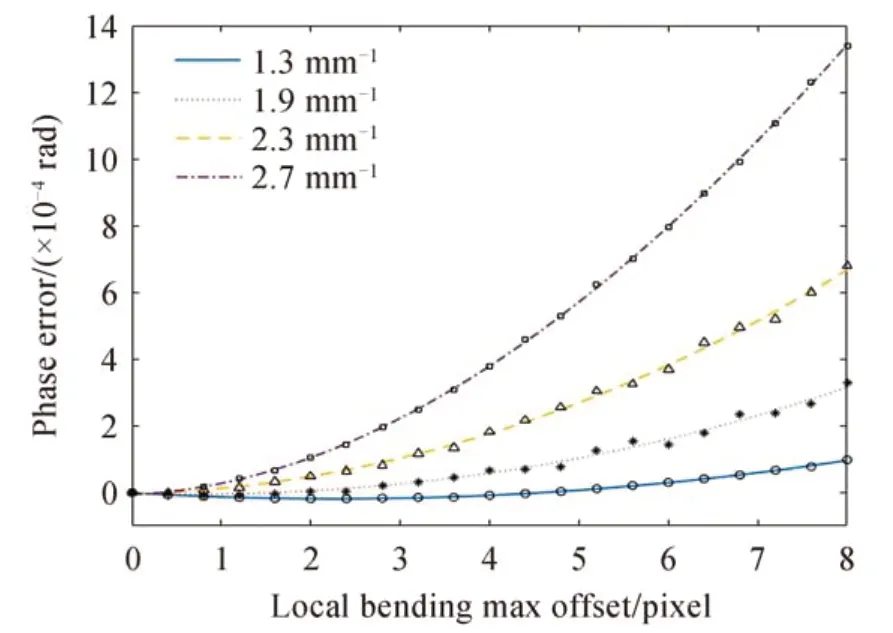
图5 局部弯曲对不同条纹频率干涉图相位反演的影响Fig.5 The influence of local bending on phase inversion of interferograms with different fringe frequencies
对比四种条纹频率系统的仿真结果发现,在任何频率下局部弯曲程度对系统相位误差影响趋势一致,弯曲程度越大相位误差越大。对比四条曲线斜率可以看出等量的弯曲情况下,条纹频率越高相位误差越大。印证了3.1 节中等量局部弯曲会对氧原子红线带来更大的多普勒相位误差的结论。即等量的畸变对条纹频率高的干涉图造成的误差更大。
3.1 节中添加干涉图局部弯曲仅在干涉图采样中心添加了弯曲范围300×300 像元的局部弯曲,为探究弯曲区域大小以及弯曲位置对多普勒相位的影响,对氧原子红线正演干涉图添加等量但不同弯曲区域大小和弯曲位置的畸变,比较不同弯曲产生的相位误差。选定目标风速100 m/s,弯曲最大偏移量1 像元,弯曲位置在采样中心,弯曲区域边长10 至300 像元的不同干涉图进行弯曲区域仿真。同样选定目标风速100 m/s,弯曲最大偏移量为1 个像元,弯曲区域50×50 像元,弯曲位置沿垂直条纹方向由采样边缘逐渐到采样中心的不同干涉图进行弯曲位置仿真,结果如图6所示。

图6 局部弯曲区域大小及位置对相位反演的影响Fig.6 The influence of the size and position of the local bending on phase inversion
结果表明等量的弯曲偏移条件下,增加弯曲区域大小时多普勒相位误差波动减小并逐渐收敛。而对弯曲位置影响的仿真表明,在干涉图上逐渐平移弯曲,相位误差随着位置变化一起波动变化,前半程波动量较小,后半程波动逐渐增大,即相同的弯曲在采样中心产生的相位误差要大于采样边缘。因此在多普勒差分干涉仪加工、装调、应用时应关注采样中心区域弯曲范围小的畸变,例如冲击噪声校正后残留的局部弯曲,必要时需进行干涉图校正以减小相位误差。
3.3 含畸变干涉图多行像元合并对相位反演的影响
反演相位时常常采取多行像元合并的方式提高信噪比,中科院西安光机所自研双视场耦合可见光DASH 样机采取16 行像元合并。孙晨等[17-18]关于调制度对相位不确定度影响的研究结果表明,相位不确定度与调制度和信噪比的乘积相关,即

式中,k为窗函数宽度,N为探测器采样数,μ为干涉图调制度,SNR 为干涉图信噪比。理想情况下条纹竖直,多行像元合并在不影响调制度的情况下提高了信噪比,降低了相位反演的不确定度。但是存在畸变的干涉图,多行像元合并时畸变区存在合并后调制度降低的情况,图7以氧原子红线为例选定采样中心存在16×100 范围弯曲,仿真了不同调制度和信噪比的情况下,不同弯曲大小16 行像元合并多普勒相位的不确定度。其中对不同信噪比的仿真选取调制度为0.6,对不同调制度的仿真选取信噪比为20,局部弯曲量选取2~14像元。弯曲达到14 像元时,条纹合并存在亮暗合并情况,条纹中部调制度下降最大。

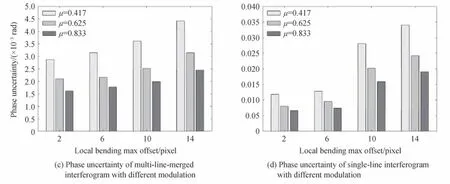
图7 不同信噪比、调制度干涉图多行像元合并对相位反演的影响Fig.7 The influence of multi-line pixel combination of interferograms with different SNR and modulations on phase inversion
对比合并前后不同信噪比和调制度的相位不确定度可以看出,各种弯曲量情况下提高信噪比和调制度都能降低相位不确定度。而对比不同弯曲量的影响能够发现,无论合并前后,局部弯曲量越大带来的相位不确定度越大。理想情况下干涉图频谱为δ 函数,但条纹弯曲使得频谱主峰存在趾瓣,实际反演相位时窗函数宽度不可能取无限大,加上频谱切趾操作,使得相位反演不确定度增大。对比合并前后的相位不确定度可以看出,无论在何种信噪比和调制度情况下,合并后的相位不确定度均小于合并前。且低信噪比、低调制度情况下合并不确定度降低,倍率要高于高信噪比调制度的情况,局部弯曲量越大合并后降低的效果越好。由此可见即使干涉图存在局部弯曲,依然可以使用多行像元合并的方式提高信噪比,降低相位反演不确定度。
4 结论
多普勒差分干涉仪在设计、加工、装调时,干涉图存在各种畸变给多普勒相位反演带来误差。本文通过对理想正演干涉图添加畸变的方式,用经典多普勒相位反演算法,仿真模拟实际干涉图反演多普勒相位时存在的相位误差。结果表明多普勒相位误差随着目标风速与干涉图畸变程度增大而增大,其中条纹局部弯曲带来的相位误差最大,弯曲量每增加一个像元系统误差增加0.113‰。而2%的畸变条件下最大系统误差仅为0.03‰,远小于等量局部弯曲带来的误差。为进一步研究局部弯曲对干涉仪图的影响,仿真计算了局部弯曲对于不同条纹频率系统的影响,以及不同弯曲范围弯曲位置的影响。结果表明等量的局部弯曲会对条纹频率高的系统产生更大影响,局部弯曲的范围越小越靠近采样中心,产生的相位误差越大。对含畸变干涉图多行像元合并过程的仿真表明,含畸变干涉图多行像元合并能有效降低相位反演不确定度,因此即使干涉图存在局部弯曲,依然可以使用多行像元合并的方式提高信噪比降低相位反演不确定度。研究结果可为多普勒差分干涉仪的设计、加工、装调指标提供定量理论依据。

