基于数据序列匹配的光纤应变传感器原位校准方法
蔡静怡,武洁雅,赵春柳,康娟,龚华平
(中国计量大学光学与电子科技学院,杭州 310018)
0 引言
桥梁健康可以使用应变测量进行评估,通常采用具有灵敏度高、稳定性好的光纤布拉格光栅(Fiber Bragg Grating,FBG)应变传感器[1-4]。但在用于监测桥梁的应变过程中,FBG 应变传感器由于长时间使用会导致其灵敏度降低,因此在实际过程中,通常将高可靠性的高精度电阻应变片作为参考传感器(Reference Sensor,RS),将FBG 应变传感器作为待校准传感器(Sensor to Be Calibrated,SBC)。由于在现场环境下,RS 传感器与SBC 传感器的数据采样不同步,时间错位等一系列不利因素,导致传感器的应变响应不一致,从而无法进行校准。
传统的校准方法是将高精度电阻应变片作为RS 传感器,在允许的误差范围内,如果SBC 传感器的应变输出与参考值的应变值相等,则认为该性能满足需求。由于桥梁形变监测系统需要全天时运行,而SBC 传感器一般不允许再组装到实验室内进行校准,所以上述方法不满足原位校准的要求[5]。
在实际应用过程中,采用特定荷载车作为激励源来研究SBC 传感器和RS 传感器的数据序列匹配方法,通过实现SBC 传感器和RS 传感器的数据匹配的一致性来研究对FBG 应变传感器原位校准的影响[6-9]。荆根强等[9]提出一种基于被动激励的结构应变监测系统在线校准方法,该方法考虑众多存在的误差,故提出期间测量误差和基本误差的计算方法对传感器在线校准。江舒等[10]设计船用FBG 应变传感器的专用校准装置,其校准方法是将传感器安装于校准装置,进行载荷的加载和卸载,并重复3 次,计算应变传感器的灵敏度。由于SBC 传感器与RS 传感器的采样时间等方面的不一致性,两量值序列的变化波形及应变数据是否一致很难判断和进行分析统计,因此会影响数据序列的匹配及原位校准灵敏度系数的计算。动态时间规整算法(Dynamic Time Warping Algorithm,DTW)[11]可用于分析时间序列,相比于其他的校准方法,该算法能很好地处理动态过程,可为序列提供局部压缩,具有计算速度快、结果直观的优点。其作用是度量时间或速度存在差异的两个序列之间的相似性[12-13],对于数据的匹配分析和序列的一致性判断及后续数据的统计分析具有良好的效果[14]。
本文以等强度悬臂梁为基础,选择精度高、一致性好、重复性好的电阻应变片作为RS 传感器,FBG 应变传感器作为SBC 传感器,在同一位置同时采集FBG 应变传感器和RS 传感器的数据,通过加载和卸载砝码来模拟汽车载荷激励源,进行原位校准方法研究。首先利用DTW 进行RS 传感器和SBC 传感器两列数据的匹配,判断传感器应变数据的一致性;然后进行应变数据的统计分析,计算两者幅值的比值作为SBC 传感器的灵敏度校准系数,从而完成FBG 应变传感器的原位校准[15]。
1 原位校准原理系统
1.1 基于电阻应变片的RS 传感器校准原理系统
电阻应变片是一种将金属丝蚀刻在可变形基底上的测量变形程度的传感器,其工作原理是利用导体的电阻随机械形变而改变的物理现象[16]。将其安装在待测结构的表面,当被测结构受力发生变形时产生与被测结构相等的应变。电阻应变片具有精度高、一致性好、重复性好的优点,是作为国标使用的应变传感器件。因此,选择高精度电阻应变片作为参考传感器。
利用砝码作为激励源,模拟桥梁载荷加载和卸载过程,通过RS 传感器和SBC 传感器对结构响应的应变测量,基于大样本数据分析计算实现原位校准特性的量化表征。其原位校准模型原理如图1。

图1 基于电阻应变片的RS 传感器原位校准模型原理Fig.1 Principle of RS sensor in-situ calibration model based on resistance strain gauge
该原位校准系统由被测量结构物、激励源、RS 传感器和SBC 传感器组成。在实验室条件下,选择等强度悬臂梁作为被测量的结构物,将砝码作为该原位校准系统的激励源,采用电阻应变片作为RS 传感器。其中RS 传感器具有准确、优秀的测量性能。在该原位校准模型中,通过砝码的加载和卸载来模拟汽车载荷激励源,进行原位校准方法研究。
1.2 FBG 传感原理
FBG 传感技术通过对在光纤内部写入的光栅反射或透射Bragg 波长光谱的检测,实现被测结构的应变和温度量值的绝对测量。而FBG 的反射或透射波长光谱主要取决于光栅周期Λ和反向耦合模的有效折射neff,任何波长λ使这两个参量发生改变的物理量都将引起FBG 波长的漂移,即有λB=2neffΛ。FBG 传感原理如图2。其FBG 传感公式为Δλ=Kε⋅Δε+KT⋅ΔT,KT为FBG 的温度灵敏度系数;Kε为FBG 的应变灵敏度系数。可以看出温度变化对于FBG 的测量具有明显的影响。本文在温度不变的情况下进行研究,即FBG应变传感器受到的应变与波长成线性关系,则上式可以化简为Δλ=Kε⋅Δε。
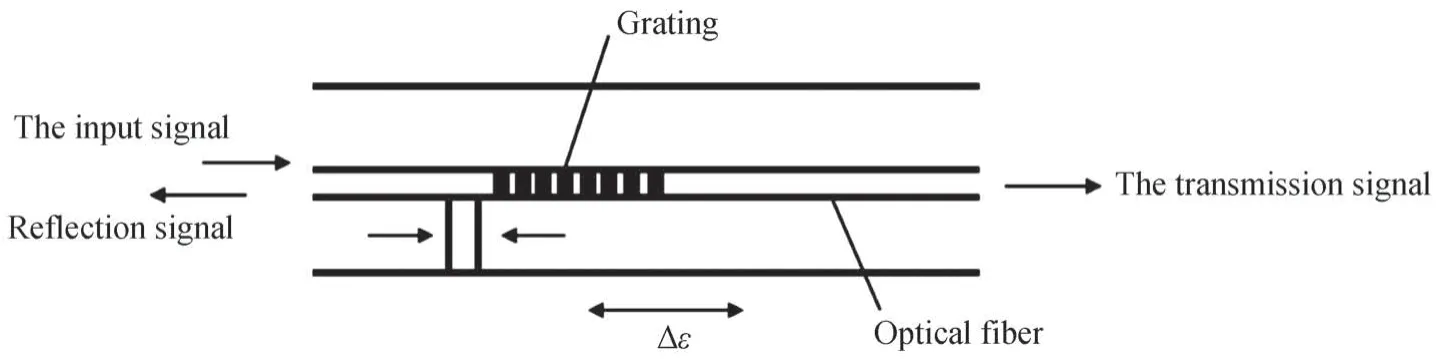
图2 FBG 传感原理Fig.2 Principle of FBG sensing
2 RS 传感器原位校准装置及方法
为了解决桥梁上通行车辆在应变检测过程中,FBG 应变传感器的长期使用导致灵敏度降低的问题,以等强度悬臂梁模型为基础搭建实验平台。实验室中以电阻应变片作为RS 传感器,FBG 应变传感器作为SBC 传感器,其中电阻应变片灵敏度系数为2.05。图3为RS 传感器与FBG 应变传感器的安装模式,电阻应变片和FBG 应变传感器采用胶水固定,其中电阻应变片被固定在等强度悬臂梁表面的中轴线位置,FBG 应变传感器被固定在电阻应变片的左边或右边,可对桥梁结构的同一应变截面进行测量。FBG 应变传感器粘接在等强度悬臂梁的上表面,在悬臂梁的顶端通过加载砝码,使等强度悬臂梁弯曲。这时,FBG 应变传感器会被压缩或者拉伸,使FBG 的中心波长产生漂移。数据采集单元分别为动静态电阻应变仪和动态FBG 解调仪,动静态电阻应变仪(协力XL2101)作用是实时读取电阻应变片的应变值,其精度为1%±1 µε;动态FBG 解调仪(SM130,MOI)作用是实时读取FBG 应变传感器的波长值,其精度为±2 pm,采样率最高为500 Hz。

图3 FBG 应变传感器原位校准装置Fig.3 FBG strain sensor in situ calibration device
图4为原位校准系统示意图,梁板上并列安装RS 传感器和SBC 传感器,RS 传感器为电阻应变片,SBC传感器为FBG 应变传感器,RS 传感器和SBC 传感器应该在桥梁(Slab)的侧方。汽车载荷每次加载到梁板上相同的位置,在汽车载荷加载和卸载的整个过程中,上位机显示动态电阻应变仪读取的电阻应变片的应变值;然后动态FBG 解调仪会对FBG 的反射波长的光信号进行解调,获取反射光中心波长值;最后上位机显示并得到FBG 应变传感器的实际波长变化值。

图4 FBG 应变传感器原位校准系统Fig.4 FBG strain sensor in situ calibration system
将FBG 应变传感器根据应变变化所得出的波形变化情况和电阻应变片根据应变变化所得出的波形变化情况记录下来,如图5。首先在没加载砝码的情况下,采集RS 传感器和SBC 传感器的数据5 s,加载后持续采集约10 s,再卸载砝码后采集5 s,继续下次加载和卸载砝码的过程,重复n次。幅值1(Δ)为光纤光栅传感器波峰平均值与初始平均值之差,幅值2(Δ)为电阻应变片波峰平均值与初始平均值之差,并重复加载和卸载砝码n次,于是得到n个灵敏度系数ki(i=1,2,3,...,n),则灵敏度校准系数ki为
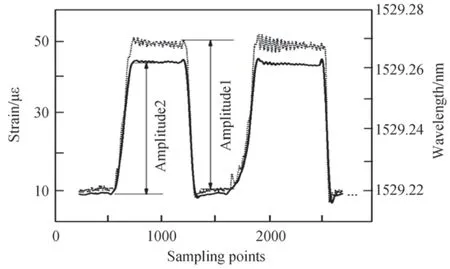
图5 电阻应变片和FBG 应变传感器幅值对比Fig.5 Amplitude comparison between resistance strain gauge and FBG strain sensor

一般情况下重复加载和卸载过程6 次进行数据统计,即可计算灵敏度校准系数,完成FBG 应变传感器的原位校准。
3 实验结果与讨论
3.1 跳变点剔除
在实际桥梁测量过程中,由于不可控的环境因素影响测量的结果,表现为在输出波形中出现异常跳变点,会对数据匹配结果产生的校准系数产生影响,因此异常跳变点剔除是需要解决的问题。
实验先采用滤波的方式以达到异常跳变点的剔除。贝赛尔滤波器是一种群延迟的线性过滤器,幅度和相位响应较为平坦,其带通的相位响应几乎呈线性。由于跳变点在频域上显示为高频信号,贝塞尔滤波器可以滤除高频信号,满足跳变点剔除的需要,因此实验选择贝塞尔滤波器进行跳变点的滤除。
图6为使用贝塞尔滤波器对原始数据进行滤波后滤除跳变点后对波形进行平滑后的图形。在图5(a)中,原始数据中看出非常明显的六个跳变点,在贝塞尔滤波器的作用下,跳变点得到滤除,如图5(b)所示。最后将滤除跳点后的数据进行移动平均平滑后,得到图5(c),因此进行后续的工作时,数据能更准确地进行匹配和计算。对数据匹配的灵敏度校准系数的影响可以认为达到了最小。
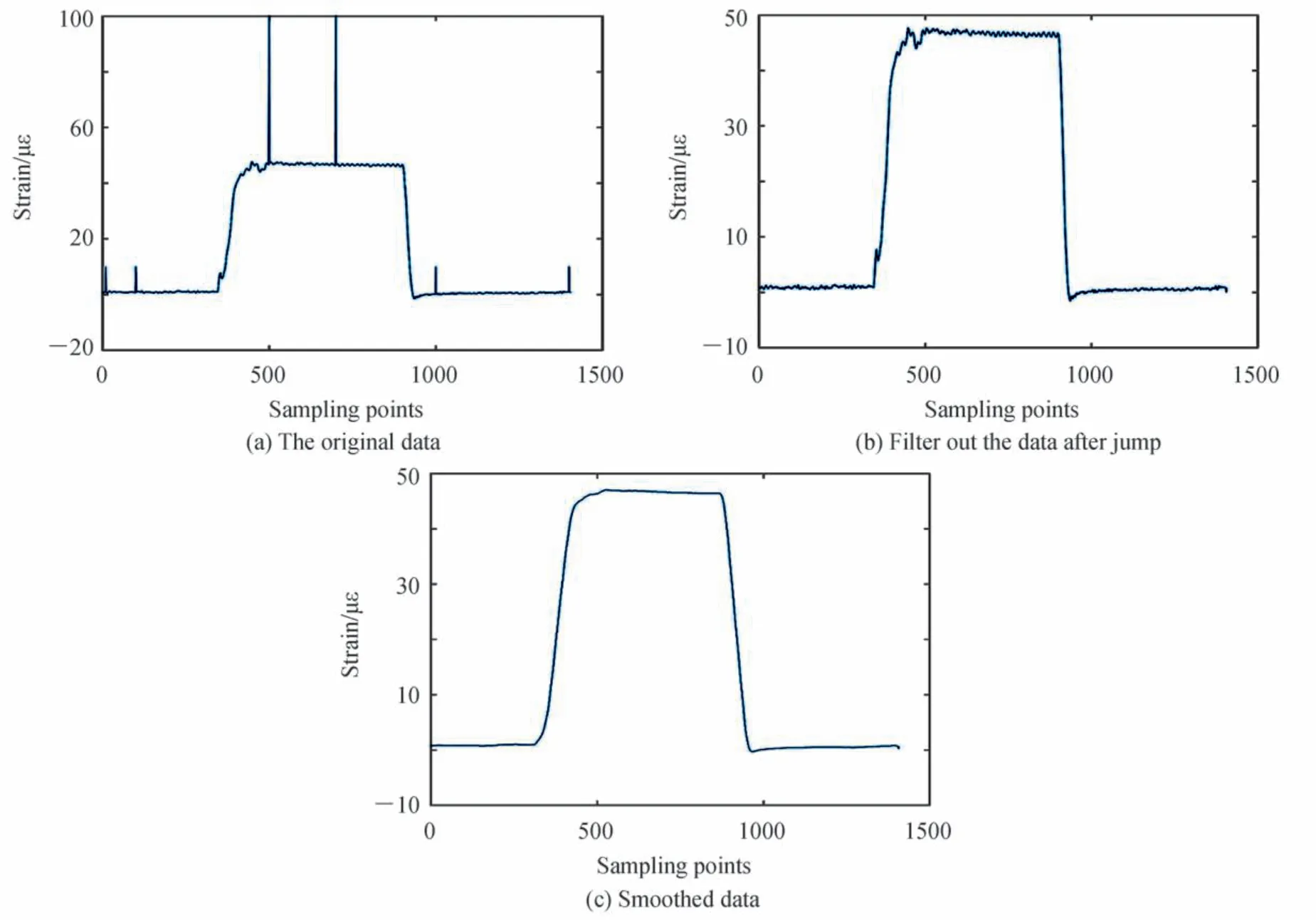
图6 跳变点滤波剔除Fig.6 Skip point filtering out
接下来需要对数据进行数据匹配,本实验采用DTW 进行应变波形的数据序列匹配。实验中可以得到电阻应变片的时间序列(R)和FBG 应变传感器的时间序列(O),用采样点表示,它们的长度分别为n和m:R序列作为RS 传感器,O序列作为SBC 传感器,序列中的每个点的值为应变序列中每一帧的特征值,其中R=r1,r2,…,rn;O=o1,o2,…,om。若n=m,则直接计算两个序列的距离;若n≠m,就需将R序列和O序列对齐。其具体计算步骤为:令RS 传感器的时间序列为R,SBC 传感器的时间序列为O,为了对齐这两个序列,需要构造一个n×m的矩阵网格,矩阵元素(i,j)表示ri和oj两个点的距离d(ri,oj),每个矩阵元素(i,j)表示ri,oj的对齐。归整路径W的形式为W=w1,w2,…,wk,W的第k个元素定义为wk=(i,j)k,归整路径W必须从w1=(1,1)开始,到wk=(|R|,|O|)结尾,以保证R和O中的每个 坐标都在W中出现。最后使用MATLAB 程序进行数据序列的原位校准。
3.2 基于电阻应变片的RS 传感器原位校准结果
实验分别采用波长为1 529 nm 和1 547 nm 的FBG 应变传感器,以依次加载和卸载砝码两次的数据为例,并统计两次应变数据来分析原位校准方法的实验结果。在实验过程中保持温度为22 ℃不变,避免温度变化引起FBG 应变传感器的波长发生漂移。图7为相同采样率下波长值为1 529 nm 的FBG 应变传感器(SBC 传感器)与电阻应变片(RS 传感器)的校准结果。首先将用RS 传感器采集到的应变数据利用贝赛尔滤波器进行跳变点的滤波剔除后,将电阻应变仪采集到的应变值和FBG 解调仪采集到的波长值进行归一化处理,然后在MATLAB 中使用DTW 算法进行RS 传感器和SBC 传感器两列数据的波形匹配。由于每个采集系统都是独立的数据记录格式,而且采样率也并不完全相同,所以数据序列通常也不一致。由图7可知,1 529 nm 波长的FBG 应变传感器与电阻应变片通过DTW 算法可以较为准确地进行数据序列的匹配。由于RS 传感器与SBC 传感器所采集到的数据是连续变量,因此采用皮尔逊相关系数计算两列波形的匹配系数,其匹配系数为0.996。

图7 相同采样率下1529 nm 波长的FBG 应变传感器与电阻应变片匹配结果Fig.7 Matching results of 1529 nm wavelength FBG strain sensor and resistance strain gauge at the same sampling rate
图8为未经过归一化处理的RS 传感器和SBC 传感器的波形图,从波形图上的平台部分取300 个数据点计算平均值,分别作为应变幅值和波长变化幅值,将电阻应变片的应变幅值和FBG 应变传感器的波长变化幅值代入式(1)进行灵敏度系数计算,重复加载和卸载砝码的过程测试6 次,得到其灵敏度校准系数如表1。通过依次加载砝码,通过静态电阻应变仪获得RS 传感器的应变值,静态解调仪获得SBC 传感器的波长值,波长值与应变值的比值即为表1中所获得的静态灵敏度系数。原位校准模拟实验六次测量的平均值为1.16 pm/με,其相对标准差为0.54%。
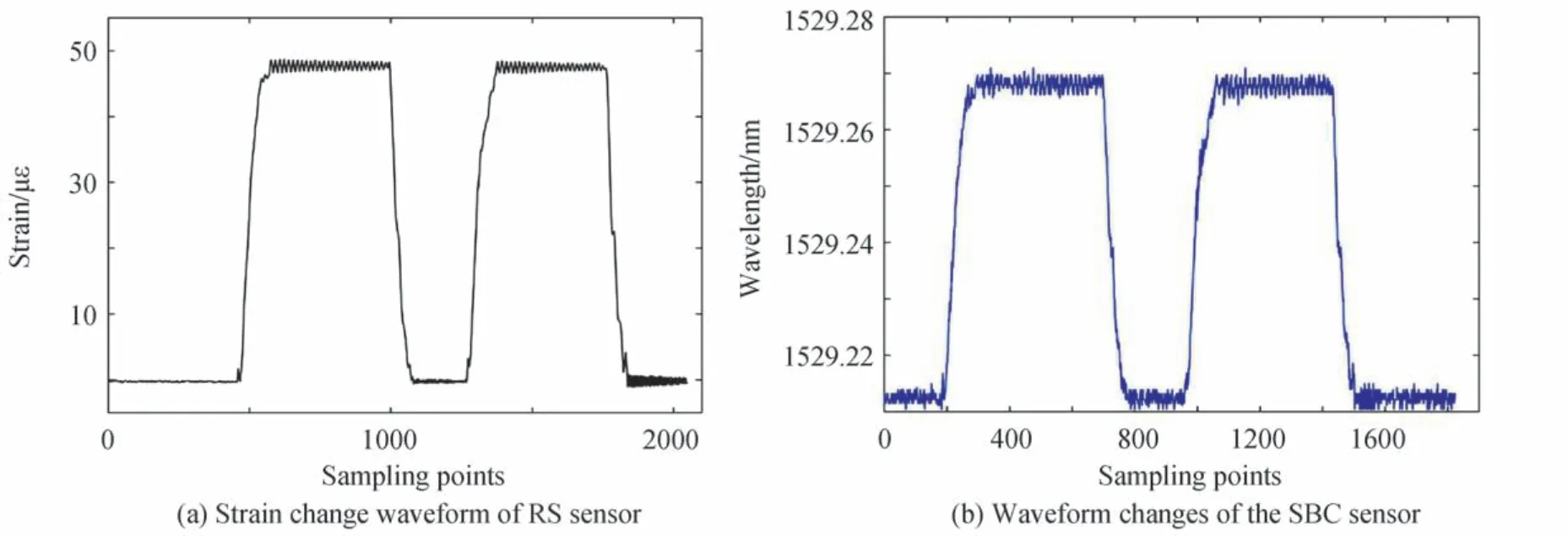
图8 相同采样率下RS 传感器和波长为1529 nm 的SBC 传感器的波形图Fig.8 Waveforms of RS sensor and SBC sensor with wavelength of 1529 nm at the same sampling rate

表1 1529 nm 波长的FBG 应变传感器灵敏度校准系数Table 1 Calibration coefficient of FBG strain sensor sensitivity at 1529 nm
同样地,对波长为1 547 nm 的FBG 应变传感器进行测试和数据处理,得到的灵敏度校准系数如表2。原位校准模拟实验六次测量的平均值为1.135 pm/με,其相对标准差为0.48%。

表2 1547 nm 波长的FBG 应变传感器灵敏度校准系数Table 2 Calibration coefficient of FBG strain sensor sensitivity at 1547 nm
为了验证原位校准方法的准确性,将1 529 nm 和1 547 nm 的这两只FBG 应变传感器在实验室条件下进行静态砝码标定。静态砝码标定的结果如图9(静态灵敏度系数已放入表1和表2中)。实验结果证明,该原位校准方法与静态标定结果基本一致,因此该方法具有较高的准确性。
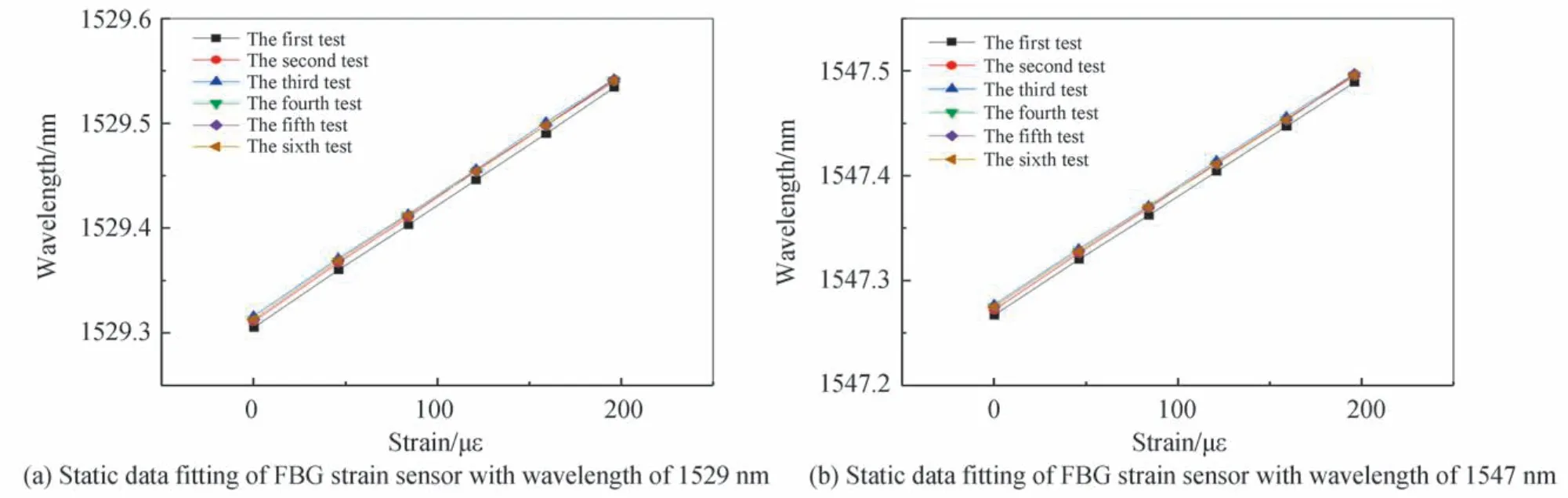
图9 波长为1 529 nm 和1 547 nm 的FBG 应变传感器的静态数据拟合Fig.9 Static data fitting of FBG strain sensors with wavelength of 1 529 nm and 1 547 nm
4 结论
针对光纤光栅应变传感器测量桥梁结构应变的准确性问题,提出一种原位校准方法。在额定载荷激励作用下,分别采集以电阻应变片作为RS 传感器和以FBG 应变传感器作为SBC 传感器的数据序列,对原始数据序列值进行跳点的去除和平滑滤波后,利用DTW 算法对RS 传感器和SBC 传感器进行应变波形的一致性判别,该算法相比于其他的校准方法,能很好地处理动态过程,具有计算速度快、结果直观的优点。然后对数据进行统计分析,计算两者幅值之比,得到FBG 应变传感器的灵敏度校准系数。实验结果表明:利用DTW 进行RS 传感器和SBC 传感器应变数据序列的匹配,匹配率达96%以上,显示两个传感器的数据序列具有高度一致性。原位校准模拟实验的结果与静态标定结果基本一致,因此该方法可用于FBG 应变传感器的原位校准。

