消除调制深度影响的相位生成载波解调方法

孙抗，何梦阳，韩毓

（1 河南理工大学 电气工程与自动化学院，河南 焦作 454003）

（2 河南省煤矿装备智能检测与控制重点实验室，河南焦作 454003）

0 引言

得益于光时域反射技术的应用，分布式光纤振动传感技术自20世纪70年代开始兴起。近年来，随着基础理论和高性能器件的不断发展，该领域已经从定性检测阶段逐渐过渡到定量检测阶段，广泛应用于安防监测、大型结构监测、油气勘探等领域［1-4］。定性检测主要任务是判断是否有扰动作用在传感光纤上并得到其具体的位置信息。对于定量检测，扰动信号的解调是极其重要的，因此也逐渐衍生出很多应用于光纤传感系统的解调方法［5］。

目前常用的解调方法主要分为零差解调和外差解调两大分支，零差解调中常用的两个主流方法分别是相位生成载波解调法（Phase Generated Carrier，PGC）［6-7］和3×3 耦合器法［8-9］；外差解调常用的方法是数字IQ 解调法［10-11］。近年来，PGC 零差检测技术以其结构简单、灵敏度高、动态范围宽、线性度好、不受光电噪声影响等突出优点在光纤振动传感系统中得到了广泛的应用［12-13］。HE J 等［14］在PGC-Arctan 算法基础上结合差分自乘（Differential Self-Multiplying，DSM）提出了一种PGC-DSM 算法，该算法具有更高的信噪比和更低的谐波失真，但在结构上极其复杂导致信号处理过程较为缓慢，影响其实时性。为了研究其在光纤传感器上的实际应用效果，FANG G 等［15］将PGC-Arctan 解调算法应用到φ-OTDR 系统中，该系统将PGCArctan 解调算法与非平衡迈克尔逊干涉仪相结合，成功在10 km 的传感光纤上解调了振动信号，但是从实验结果来看，该方法会受到系统调制深度和光强稳定性的影响，导致波形存在较大的失真现象。之后，YU Z等［16］提出了一种适用于干涉型光纤传感器的高稳定性低谐波失真的PGC 解调技术，信噪比与失真（Signalto-Noise-And-Distortion，SINAD）比传统的PGC-Arctan 高13.13 dB，但是其能够探测的频率较低，对于1 kHz 以上的信号探测效果较差。ZHANG S 等［17］针对载波调制深度和载波相位延迟两个因素分析了PGC解调算法的局限性，并提出一种改进的PGC-DCDM（Differential Cross Dividing and Multiplying）算法，其解调结果在一定调制深度和相位延迟范围具有较高的稳定性和较低的谐波失真。

通过上述分析，PGC-Arctan 解调算法及其在光纤振动传感系统中的应用研究已经较为深入，但是其解调结果的准确性和稳定性严重依赖于系统的调制深度。本文提出一种结合微分自相除（Differential Selfdivision，DSVV）的PGC-Arctan 解调算法（PGC-DSVV），能够消除调制深度对PGC-Arctan 解调算法的影响，可有效提高解调算法的稳定性和准确性。

1 基本原理

1.1 PGC-Arctan 原理及其问题

PGC 技术是在干涉仪的传感臂上加入一个极高频的载波信号，使振动信号成为其边带信号，通过对叠加后的信号进行一系列滤波、混频以及离散运算等操作，去除噪声信号对原始振动信号的干扰，从载波信号中解调出振动信号［18］。

PGC-Arctan 解调算法原理如图1所示，其中Interference signal 为光纤振动传感器中返回的后向瑞利散射光经光电探测器（Photoelectric Detector，PD）后输出的干涉信号。经过光电探测器输出的干涉信号可表示为

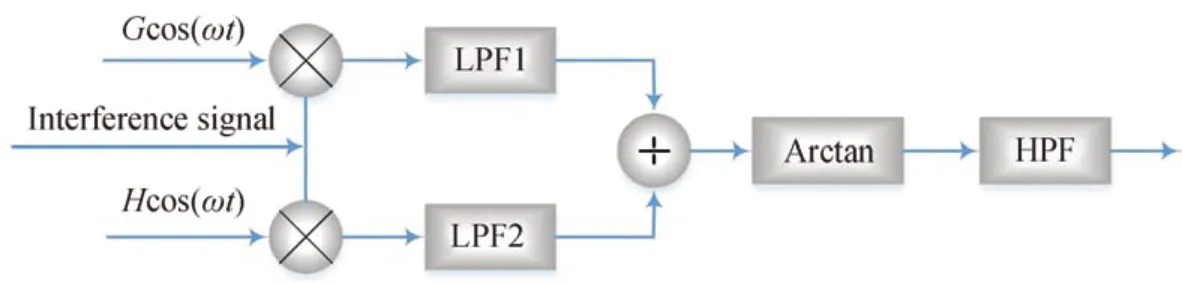
图1 PGC-Arctan 算法结构Fig.1 Schematic diagram of the PGC-Arctan algorithm

式中，A表示与光纤入射光幅值和散射系数有关的定值；B表示干涉的相干长度；C表示调制深度；D表示振动信号幅值；ω0表示载波信号的角频率；ω表示振动信号角频率；φ（t）表示光在光纤传播过程中由外界噪声（如低频噪声分量）等因素引起的相位差。

将式（1）通过贝塞尔函数展开，并分别与基频信号和二倍频信号混频。混频之后两路信号分别表示为

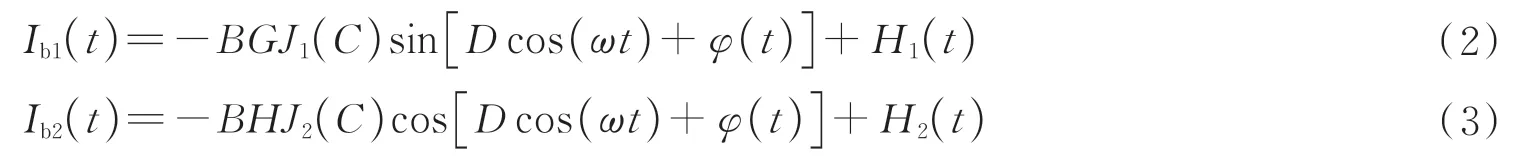
式中，G、H分别表示基频信号幅值和二倍频信号幅值；H1（t）、H2（t）分别表示混频之后两路信号光中的高频分量。

混频后的两路信号分别进行低通滤波（Low-Pass Filter，LPF）处理，然后两路信号进行相除和反正切运算，最后经过高通滤波器（High-PASS Filter，HPF）得到解调结果为

从式（4）看出，传统的PGC-Arctan 算法解调结果中包含基频信号幅值（G）和二倍频信号幅值（H）以及调制深度（C）的贝塞尔函数值。通常情况下令G与H相等，C值为2.63 rad 时才能达到较为理想的解调效果。然而在实际应用中，调制深度容易受系统光源和环境因素等方面的影响，无法保持恒定值，从而使解调效果出现失真，严重时可能无法成功解调出振动信息。

1.2 PGC-DSVV 原理

PGC-DSVV 算法结构如图2所示，与传统PGC-Arctan 算法一致，干涉信号经混频后得到两路信号光分别为Ib1（t）和Ib2（t），之后分别经过低通滤波器LPF1、LPF2，滤除掉信号中的两个高频分量H1（t）和H2（t），结果可表示为

图2 PGC-DSVV 算法结构Fig.2 Schematic diagram of the PGC-DSVV algorithm

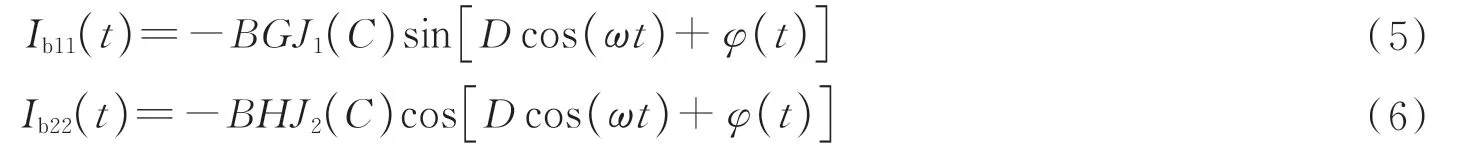
然后将Ib11（t）、Ib22（t）分别分成两路信号光，进行微分自相除运算得到

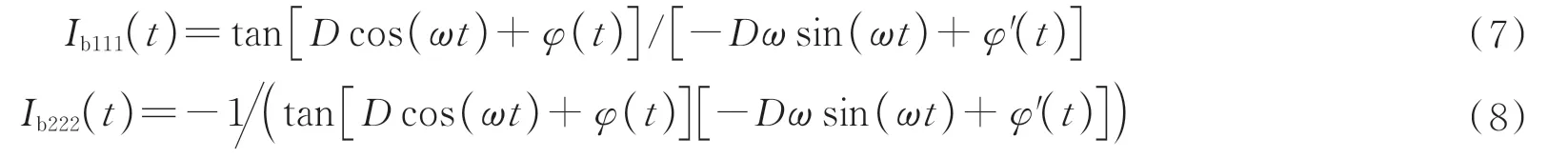
式（7）、（8）相除并取绝对值可得到

对得到的信号进行开方和反正切运算即可得到

最后对其进行高通滤波，以滤除由环境等外界因素引起的低频噪声φ（t），即可解得原始的振动信号

结合以上分析过程，可以清晰看出，通过提出的PGC-DSVV 解调算法，可以有效将振动信号从高频干涉信号中解调出来。由式（11）可知，解调结果不再受调制深度的影响，并且也不需要在解调过程中保证基频信号和倍频信号的幅值相等。

2 仿真分析

利用MATLAB 平台搭建仿真模型，从调制深度和信噪比（Signal-to-Noise Ratios，SNR）两个方面分析PGC-DSVV 算法的解调效果。在研究过程中，分别利用幅值误差和总谐波失真（Total Harmonic Distortion，THD）两个参数反映解调结果的线性失真和非线性失真，计算公式分别为

式中，ɑt和ɑ0分别为解调信号的幅值和原始信号的幅值；G1和Gi（i=2，3，···）分别代表基波和各谐波分量幅值。

2.1 不同调制深度下常见算法解调效果对比

在仿真的过程中，待解调信号为频率2 kHz、幅值6 rad 的正弦信号，分别设置1.5 rad、2.37 rad、2.63 rad和3.5 rad 四个C值，将该算法与目前常见的几种算法进行对比，解调结果时域波形如图3所示。图3表明，PGC-Arctan 算法和PGC-DCM（Differential and Cross Multiplying）算法在不同C值下解调效果很差，前者非线性失真严重，后者线性失真情况严重；相比之下，PGC-DSVV 算法的解调信号在时域波形上表现出良好的解调效果。

图3 不同C 值下四种算法解调结果Fig.3 Demodulation results of the four algorithms under different C values

分别对C=1.5 rad、2.37 rad、2.63 rad 和3.5 rad 时各种常见算法的解调结果进行频谱分析，如图4。可以看出，在C值相同的情况下，PGC-DSVV 算法得到的谐波分量和底噪水平都为最佳；在C值不同的情况下，PGC-DSVV 算法对C值的变化并不敏感，基本处于稳定状态。

图4 不同C 值下四种算法频谱图Fig.4 Spectrogram of the four algorithms under different C values

分别定量计算4 个C值下各种解调算法的幅值误差和THD 值，结果如表1所示。数据表明，PGCDSVV 算法的幅值误差最小值是0.077%，相比其他三种算法分别低0.388%、0.713%和2.183%，THD 的最小值相比于其他三种算法分别低0.095%、0.562%和0.434%。综合以上分析，从时域、频域以及数值域对常见解调算法进行对比，结果表明DSVV 算法解调效果优于其他算法。

表1 不同C 值下四种算法参数对比Table 1 Comparison of parameters of the four algorithms under different C values

2.2 不同信噪比下PGC-DSVV 算法解调效果分析

在实际应用中振动信号存在不同程度的噪声干扰，会对解调效果造成影响。为了研究PGC-DSVV 算法对不同信噪比振动信号的解调效果，给频率为2 kHz，幅值为6 rad 的正弦信号加入不同程度的高斯白噪声分量，使其信噪比分别达到40 dB、30 dB、20 dB 和10 dB，设置系统调制深度为2.63 rad，得到该算法解调后的时域波形及对应的频域波形，结果如图5所示。从图5中可以初步判断，随着信噪比的降低，解调后波形的信号幅值近乎不变，底噪水平和谐波分量会增加。

图5 不同SNR 下PGC-DSVV 解调结果Fig.5 Demodulation results of the PGC-DSVV under different SNR

表2记录了对不同信噪比振动信号的解调失真数据。数据表明，在其他条件不变的情况下，信噪比与解调失真呈反比，即随着信噪比降低，幅值误差和THD 值增加，解调波形的失真程度加重。但是，在信噪比低至10 dB 时，幅值误差为0.130%，THD 值为0.090%，相较于没有噪声干扰时分别增加了0.053%和0.042%，仍然能够满足在实际应用中的需求。

表2 不同SNR 时PGC-DSVV 算法参数Table 2 Parameters of PGC-DSVV under different SNR

3 实验与结果分析

搭建了一套分布式光纤振动传感系统，主要由光路结构、传感光纤和上位机三部分组成，其结构如图6所示。从激光光源发出的连续光由声光调制器（Acoustic Optical Modulator，AOM）调制，调制后的脉冲光通过掺铒光纤放大器（Erbium-Doped Fiber Amplifier，EDFA）进行放大并经滤波器（Filter）滤除EDFA 产生的噪声，之后通过环形器（Cir）注入传感光纤。传感光纤返回的后向瑞利散射光通过Cir 之后，经过耦合器（Optical Coupler，OC）被分为两部分，一部分先通过压电陶瓷片（Piezoceramic，PZT）驱动的延时光纤，再经过法拉第旋转镜（Faraday Rotating Mirror，FRM）反射，另一部分直接经过法拉第旋转镜反射，之后在耦合器中进行干涉，最后干涉信号通过光电探测器（PD）转换为电信号，由数据采集卡（Data Acquisition Card，DAQ）采集后存入上位机。其中，光源采用线宽为5 kHz，峰值功率为20 mW，波长为1 550 nm 的窄线宽激光光源（LD-PD-1550-2-16-SM）；AOM 的频移为200 MHz；EDFA 的最大输出功率达到200 mW；弱反射光栅布拉格光纤的长度为200 m，−3 dB 带宽是0.7 nm，光栅间隔为1 m，共有199 个反射光栅；光电探测器的探测带宽为100 MHz；数据采集卡的采集速率为1.2 Gsps。依托搭建的实验平台，分别在不同C值情况下对常见算法进行对比分析，主要针对解调效果的线性失真（幅值误差）和非线性失真（THD 值）两个方面。

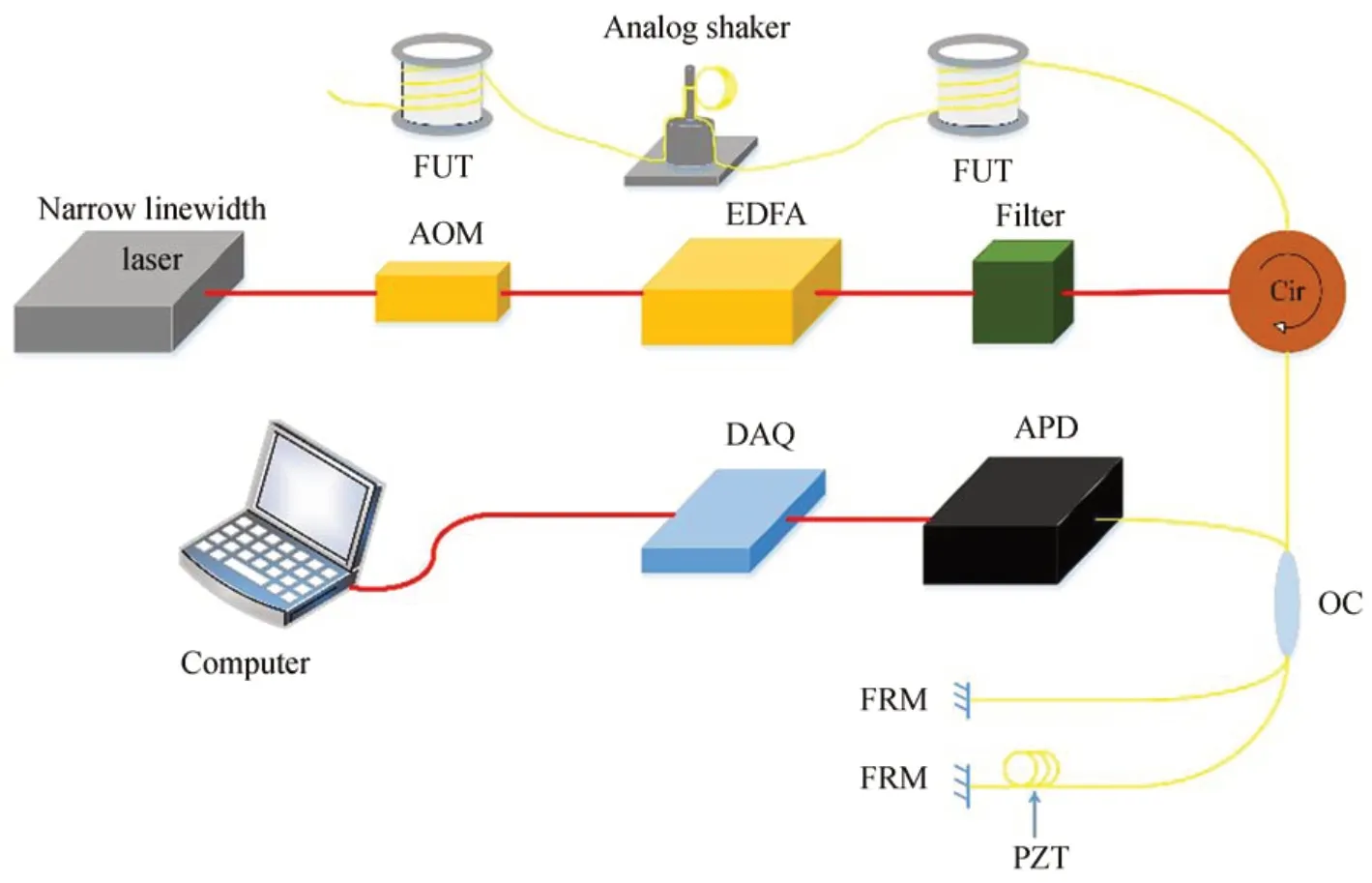
图6 传感系统结构Fig.6 Sensing system structure diagram

采用集成化的光纤振动传感器进行实验，图7是实验设备。将传感光纤50 m 的位置缠绕在模拟激振器上，缠绕方式为直径10 cm 的环形缠绕。波形发生器驱动激振器产生频率为2 kHz，幅值为6 V 的振动信号，利用PGC-DSVV 算法对采集到的后向瑞利散射信号进行解调，实验结果如图8所示。结果表明，PGC-DS‐VV 算法能够还原施加在被测光纤上的振动信号。

图7 实验设备Fig.7 Experimental equipment

图8 PGC-DSVV 解调结果Fig.8 Demodulation results of the PGC-DSVV

图9（a）、（b）分别是每种算法在不同C值下的幅值误差和THD 值。实验结果表明，就各种解调算法对C值的敏感程度而言，PGC-DSVV 算法的幅值误差和THD 值对C值得敏感程度最低，在不同C值情况下解调效果基本一致。算法的解调效果通过幅值误差和THD 的最小值进行对比，PGC-DSVV 的幅值误差最小值为0.105%，比其他三种算法分别低0.525%、0.858%和2.900%；THD 最小值为0.068%，比其他三种算法分别低0.101%、0.662%和0.595%。将实验得到的数据与仿真得到的数据进行对比，结果发现，同等条件下，实验的解调失真度略高于仿真。考虑到实验环境下振动信号在传播过程中受到外界噪声的相位调制以及光源的频率漂移产生的影响，导致振动信号的信噪比降低，从而造成失真加重，与仿真得到的结论一致。

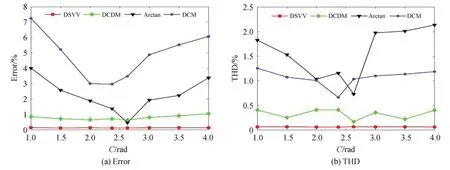
图9 不同C 值下四种算法实验结果Fig.9 Experimental results of the four algorithms under different C values

动态范围也是解调算法在实际应用中值得关注的一个因素。设定解调算法的线性失真或者非线性失真超过预先给定的阈值为解调失败，定义动态范围为同一频率下能够成功解调的信号最大幅值与最小幅值之比。表达式为

式中，R为动态范围，单位是dB；Vmax，Vmin分别是成功解调的信号最大幅值和最小幅值，单位是V。

图10是实验得到的四种解调算法的动态范围。实验结果表明，PGC-DSVV 算法的解调信号带宽和动态范围均比其他算法大。PGC-DSVV 算法在频率为200 Hz 时动态范围是62.5 dB，频率为5 kHz 时动态范围是31.5 dB，动态范围随着解调信号频率的增加逐渐降低，并且降低的趋势越来越平缓。造成这种变化的原因是：1）随着解调信号频率的增加，系统的调制频率需要大幅度增加，从而对动态范围造成影响；2）局限于解调系统的结构，获取的微弱高频信号会存在较低的信噪比，从而导致解调失真增加，降低动态范围。

图10 四种算法动态范围Fig.10 Dynamic range of the four algorithm

4 结论

针对PGC-Arctan 算法解调效果受调制深度影响的问题，本文提出一种改进的PGC-DSVV 解调算法，通过在算法框架中引入微分自相除运算环节，消除两路混频信号中调制深度的影响。仿真从调制深度和SNR 两个方面分析了该算法的稳定性，并搭建完整的实验平台，对比分析不同的调制深度下常见算法的性能指标。数据表明，PGC-DSVV 算法的解调信号幅值误差为0.105%，THD 值仅为0.068%，比PGCDCDM 算法降低了0.525%和0.101%。实验证明了PGC-DSVV 解调算法能够更好地应对调制深度漂移，具有更高的稳定性和更低的谐波失真，可为高性能光纤振动传感器的应用提供技术支撑。然而该算法对超高频信号解调效果较差，研究过程中没有充分考虑相位延迟对解调算法的影响，提高改进算法的解调频率带宽，使其能够应用于要求更高的领域是下一步的研究方向。