Rouch é定理的应用及其逆定理的探讨

廖家奇，张和平，胡余旺

（1.河南工业大学 漯河工学院，河南 漯河 462000；2.信阳师范学院 数学与统计学院，河南 信阳 464000）

复变函数论教科书中，Rouché定理是这样叙述的：若 f（z），g（z）在闭单位圆中解析，且在，f（z）≠0，g（z）≠0，如果z∈C时，，则N（f，C）=N（g，C），其中N（f，C），N（g，C）分别表示f（z），g（z）在C所围区域内零点的个数。

应用Rouché定理证明代数学基本定理，若任一n次方程为

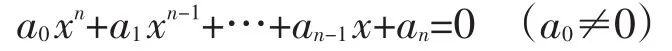
则该方程有且只有n个根（几重根就算作几个根）。

证明：令f（x）=a0xn，g（z）=a0xn+a1xn-1+…+an-1x+an当x在充分大的圆周上时，取

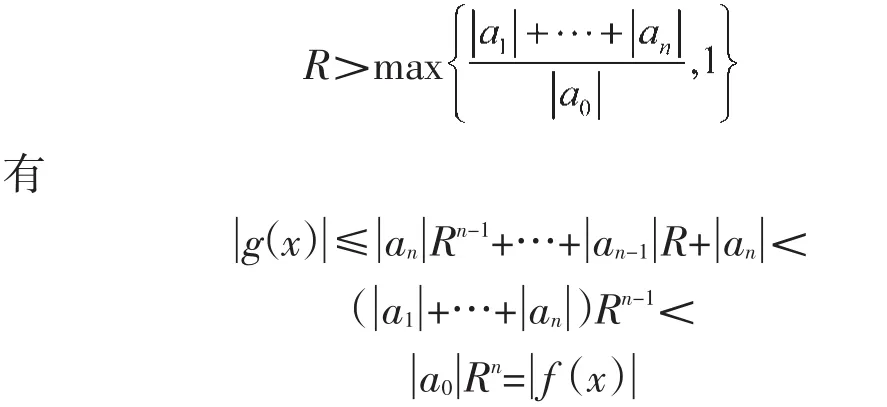
这两个方程有相同个数的根，而a0xn=0在内有一个n重根x=0。因此原n次方程在内有n个根。

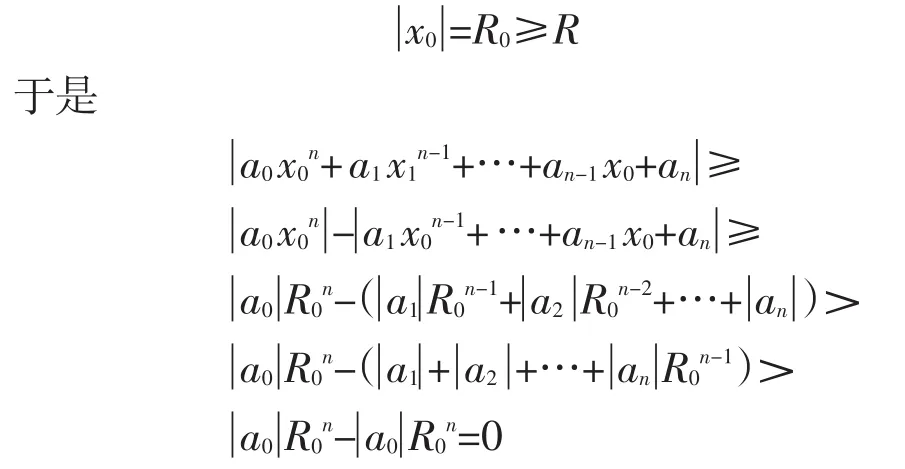
应用Rouché定理证明单叶解析函数一个重要性质。若函数f（x）在区域R内单叶解析，则在R内f′（x）≠0。

证明：若有 R 的点 x0使 f′（x）=0，则 x0必为f（x）-f（x0）的一个n级零点（n≥2），由零点的孤立性，故存在a＞0，使得圆周上，f（x）-f（x0）≠0在C的内部，f（x）-f（x0）及 f′（x）无异于x0的零点。

f（x）-f（x0）-a

该方程在圆周C的内部也恰好有n个零点。但是这些零点都不是多重点，这是因为f′（x）在C的内部除x0外无其他零点，而x0显然不是f（x）-f（x0）-a 的零点。

令x1，x2，…，xn代表f（x）-f（x0）-a在C 的内部的n个相异零点，于是

f（xk）=f（x0）+a （k=1，2，…，n）

这与f（x）的单叶性假设矛盾。所以在R内存在

f'（x）≠0

在1962年T.Estermann［1］将Rouché定理加强如下：若 f（z）·g（z）在中解析，且存在同阶的有限Blaschke乘积a（z）与β（z），使当z∈C时有

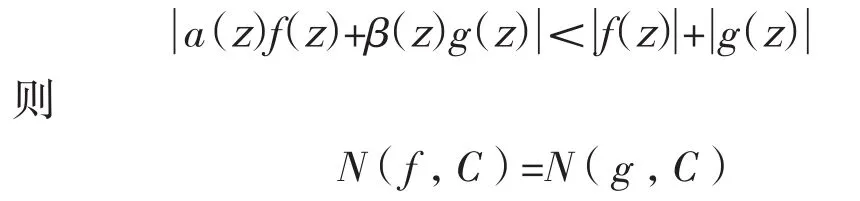
这种加强形式并没有解决Rouché定理之逆问题，但却提供了解决这个问题的途径。

为了证明Rouché定理的逆定理，先简要介绍一下Blaschke乘积。

令{zn}是单位圆盘中的点列，且

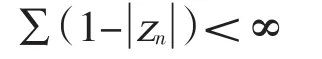
则以{zn}为零点的函数为

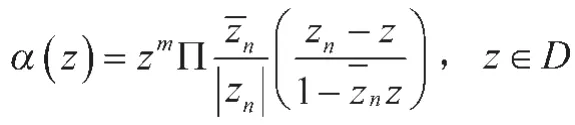
该函数称为Blaschke乘积，其中m是序列{zn}中的零点个数，当m=0时，显然，因此a（z）又称为么模函数。

为证明Rouché定理的逆定理，先引进一个引理。

引理已知f（z），g（z）在上解析，且当时，f（z）≠0，g（z）≠0，则存在有限的Blaschke乘积a（z）与β（z），使当z∈C 时，有

证明：当z∈C时，令

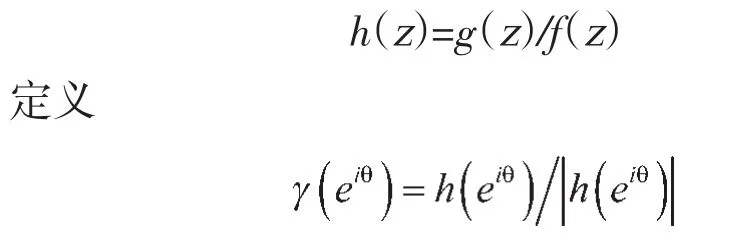
则在C上γ（z）是连续的么模函数，而且在C上没有零点，则有Davie，Gamelin和Garnett的结果，存在有限的Blaschke乘积a（z）与β（z），使当z∈C 时，有

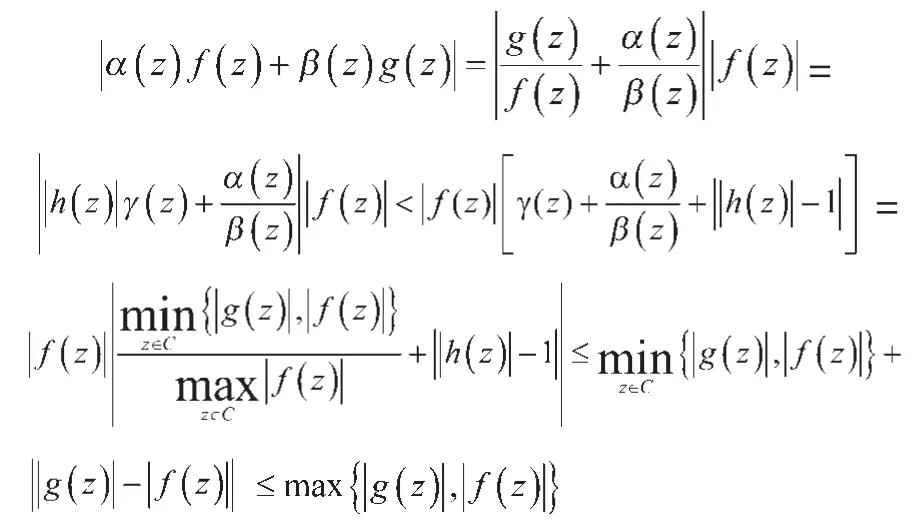
引理证毕。

定理 假设β（z），g（z）在上解析，上没有零点，若N（f，C），N（g，C）分别表示f（z）与g（z）在所围区域内零点的个数（重零点以重数计），则N（f，C）=N（g，C）的充要条件是存在同阶的Blaschke乘积α（z），β（z），使当时，有

证明：（必要性）假设N（f，C）=N（g，C），据引理，存在有限的Blaschke乘积α（z）与β（z），使当时存在：

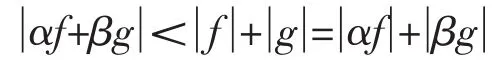
因而据Estermann加强的Rouché定理，在C的内部αf与βg零点个数相同，即

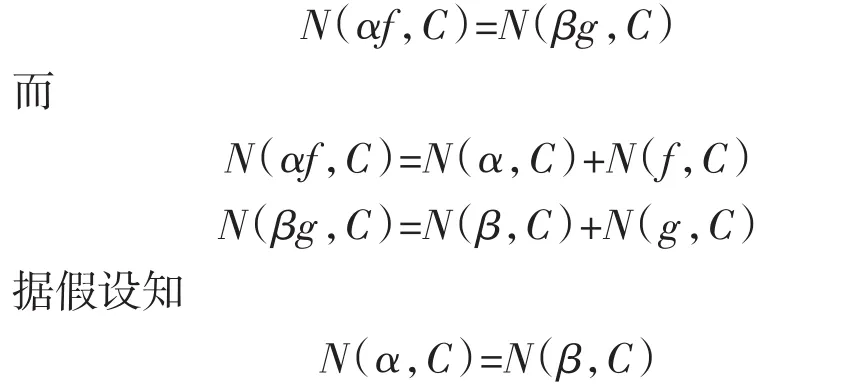
由此可知α（z），β（z）是同阶的［2］。

（充分性）假设存在同阶的Blaschke乘积α（z）与β（z），使当z∈C时，有

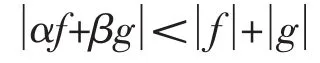
则当z∈C时，有

据加强的Rouché定理，有

由以上的定理即可得出推论1和推论2。

推论1假设f（z），g（z）在上解析，且当z∈C时，f（z）≠0，g（z）≠0，则N（f，C）-N（g，C）=m的充要条件是有限的Blaschke乘积α（z）与β（z），使

N（β，C）-N（α，C）=m

且z∈C时，有

其中，m是非负整数［3］。

推论1的证明方法类似于定理的证明。

推论2 如果存在有限的Blaschke乘积α（z）与β（z），使当z∈C时，α与β的零点个数相同，且

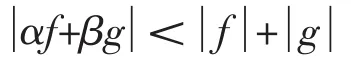
则存在有限的Blaschke乘积α*（z）与β*（z），使

证明：有定理知，因N（α）=N（β），则N（f）=N（g），又据引理，存在有限的存在有限的Blaschke乘积与α*（z）与β*（z），使得