Quantitative study on the tension-compression yield asymmetry of a Mg-3Al-1Zn alloy with bimodal texture components

Lingyu Zho ,Wnho Chn ,Bin Zhou ,Cong H ,Chngjin Yn ,Zhoyng Jin ,Huihui Yu,Yunhng Xin

a School of Mechanical Engineering,Yangzhou University,Yangzhou 225127,China

b Key Laboratory for Light-weight Materials,Nanjing Tech University 10009,China

cNational Institute for Materials Science,1-2-1 Sengen,Tsukuba,305-0047,Japan

d Institute of Corrosion Science and Technology,Guangdong 510070,China

e Institute of Applied Physics,Jiangxi Academy of Sciences,Nanchang 330029,China

Abstract This study demonstrates the yield asymmetry in Mg-3Al-1Zn alloy containing both ND-texture (c-axis// ND (Normal direction)) and TD-texture (c-axis// TD (Transverse direction)) in a quantitative view.The results showed that the yield asymmetry is strongly dependent on the distribution of bimodal texture components,on the basis of the successful establishment of the quantifie relationship between pre-deformation parameters and texture components distribution.It’s meaningful for providing key reference to texture design.Mechanical behavior of bimodal textured Mg alloy under tension and compression was tested.CYS/TYS (compressive yield stress/ tensile yield stress)equal to 1 is obtained,implying that the yield asymmetry is eliminated when two textures distribute at specifi fractions.The corresponding mechanism for the texture-dependence of tension-compression yield asymmetry is revealed by the analysis of slip/twinning activities and a compound use of the activation stress difference of slip/twinning (ΔStress) and geometrical compatibility factor (m＇) between neighboring grains.Balanced activity of {102} twinning and a quite similar boundary obstacle effect against slip/twinning transfer under tension and compression accounts for such good symmetry performance.

Keywords: Mg alloy;Texture;Mechanical anisotropy;Twinning;Slip.

1.Introduction

Magnesium (Mg) alloys have received significan interest in response to a requirement of weight-saving in the automotive,aerospace and portable electronics industries [1,2].However,besides of a lower strength and a poor formability compared to its counterpart aluminum alloy,an intensive tensioncompression yield asymmetry in highly textured Mg products,in which compression yield strength (CYS) greatly different from that of tension yield strength (TYS) is another bottleneck limiting the wide application of commercial Mg alloy[3].For example,the compressive-tensile yield asymmetries is above 1.6 as reported in traditional Mg-Al-Zn series alloys[4,5],and the yield strength in compression is about 0.4-0.8 of that in tension when loading along extrusion directions in commercial Mg extrusion alloys [1].This will cause a poor bending ductility and restrict its widespread application in fatigue-critical components,such as suspension control arms.Failure might occurred earlier than expected [6].As Mg alloys becoming more available in the biomedical applications,like vascular stents,considerable bending deformation will be introduced to the high-curvature part of stents after balloon expansion [7].In the cross-section of bent strut,tensile and compressive strain exists in pairs.With higher CYS,the tensile strain would be larger than compressive strain,thus leading to severer strain localization of stents after deployment.The strain localization may cause the failure of balloon expansion and lower the degradation uniformity [8].

The presence of tension-compression yield asymmetry in Mg alloys is closely related to the activation of {102}twinning which has a much lower critical resolved shear stress (CRSS) than non-basal slips [9,10].Great efforts have been made to reduce tension-compression yield asymmetry.The methods to reduce tension-compression yield asymmetry includes grain refinemen [11,12],preparation of bimodalgrained structure [13],strengthening twin system by precipitation [14,15],pre-twinned treatment [16,17],weakening texture[18-20]etc.The use of grain refinemen to improve yield asymmetry can be understood as:yield asymmetry is closely related with the activity of {102} twinning [5],while {102}twinning is favorable in coarse grains [17].A transformation of deformation mode from the {102} twinning to slips can take place when samples with grain size bellow a critical value [21].Yinet al.reported that the critical grain size is approximately 0.8 μm for AZ31 alloy,below which no yield asymmetry appears,no matter whether the texture exists or not [11].Another method to reduce the yield asymmetry is to decrease the CRSS differences between slip and twining by precipitates.A very recent research predicts a much higher precipitation hardening on twinning than the classical Orowan precipitate hardening of basal slip and prismatic slip [14].

In terms of texture weakening strategy,the mechanism is mainly related to a balance of the activities of slips and{102}twinning.An intense basal texture of wrought Mg alloys can be weakened or tilted through the addition of rare earth elements [22,23] and various mechanical process such as cold rolling [24],equal channel angular extrusion [25],and differential speed rolling [26].Differential speed rolling is a new processing technique that introduces a strong shear deformation and modifie the texture and microstructure of Mg sheets [27,28].However,in addition to thickness limitations,this technique has some disadvantages such as the formation of texture gradient and a non-uniform deformation through thickness [26,29].Furthermore,some processing technologies are complex and not economical,and sometimes are not very effective.Easily operated and effective methods are needed.

Recently,it has been found that the yield asymmetry of Mg alloys can be suppressed by composite extension twin structure which results in multi-deformation modes during both the tension and compression [5,30].However,the high thermal stability of extension twins makes it difficul to achieve a fully recrystallized structure by annealing treatment.If samples are annealed at quite high temperature,it can cause an unexpected grain coarsening.Recently,it is reported that when a 5.5%pre-compression along the normal direction (ND) prior to the formation of {102} twins is conducted,the stored energy increases and recrystallization behavior of sample with twins will be changed.It is found that after annealing at 250 °C for 1 h,a fully recrystallized structure with the refine grains will be achieved and the orientations of the {102} twins will be kept well after recrystallization [31,32].This could provide a new method to use {102} twinning to tailor the strong basal texture.Thus,the concept of bimodal texture containing both hard grains and soft grains has been proposed.A recent study in our group reported that bimodal texture distribution poses an important effect on the activation of deformation modes,especially {102} twinning.The initial deformation was concentrated in soft oriented grains causing different strain-stress curves and strain hardening features [33].To our knowledge,no studies have establish a quantitative relation between bimodal textures with different fractions of texture component and tension-compression yield asymmetry.

In the present work,bimodal textures with different factions of texture component with basal poles largely parallel to the ND and texture component with basal poles largely parallel to the TD were successfully prepared by precompression and annealing of AZ31 Mg plate.The relation between the tension-compression yield asymmetry and bimodal texture components was built and corresponding mechanism was further revealed by a compound analysis of activities of slips/twinning and grain boundary effect.

2.Experiments and methods

2.1.Sample preparation and mechanical tests

The starting material used in this study was a commercial hot-rolled AZ31 Mg alloy (Mg-3.6%Al-1.0%Zn-0.5%Mn)plate with 20 mm thick.Here,the initial ingot is hot rolled at 420 °C from 165 mm thick to 20 mm thick through 7 passes.The microstructure of as-received materials is shown in Fig.1a.The preparation of bimodal texture contains two steps,pre-deformation and annealing treatment,which are schematically illustrated in Fig.1b.The pre-deformation procedure includes a 7% cold rolling along ND and a subsequent compression along TD to different strains.The cold rolled plate was cut into blocks 32 mm (TD) × 22 mm(RD) × 18 mm (ND) for TD compression.A type of single texture and four types of bimodal texture were prepared in the present work.While the BT1 sample (i.e.,bimodal textured sample),BT2 sample,BT3 sample,BT4 sample were subjected to compression along the TD by 2.5%,3.8%,5.4%,7.0%,respectively.After several heat treatment tests,the fina annealing treatment was determined as annealing at 250 °C for 3 h.The ST sample is the sample subjected to a 7% cold rolling along ND direction (without TD compression) and annealed at 250 °C for 3 h,subsequently.During annealing in the muffl furnace,the samples were covered with magnesium oxide powder and the surfaces of the samples were barely oxidized after annealing.Here,bimodal texture means there are two types of texture component,texture component with basal poles largely parallel to the ND and texture component with basal poles largely parallel to the TD.The specimens for tensile tests have a total length of 30 mm,gage length of 10 mm,width of the holding section of 7 mm,width of gage section of 4 mm,and the thickness of 2.5 mm.The compressive specimens are blocks with 10 mm (TD) × 8 mm (RD) × 8 mm(ND).All tensile and compressive tests were performed at room temperature on a Shimadzu AG-X mechanical testing system at a strain rate of 0.001 s−1.Graphite was used to reduce friction between the holder and the samples during compression.All specimens before tension and compression tests were annealed in a muffl furnace at 250 °C for 3 h,and cooled in the air.All mechanical tests were repeated three times.

Fig.1.(a) Inverse pole figur of as-received AZ31 plate and (b) schematic diagram and stress-strain curve (compression along TD of the 7% cold rolled sample) showing the preparation of the samples with bimodal texture.Precomp.(2.5%),Pre-comp.(3.8%),Pre-comp.(5.4%) and Pre-comp.(7.0%)means pre-compression along the TD by 2.5%,3.8%,5.4% and 7.0%,respectively.

2.2.Examination of microstructure

Specimens for optical microscopy were carefully ground with a series of SiC sand papers (800 grit and 1000 grit),polishing and etching with the acetic picral solution (2.0 mlacetic acid +1.0 g picric acid +2 ml distilled water +16 ml ethanol (99.5%)).In order to disclose the distribution of bimodal textures and the texture changes before and after annealing,X-Ray diffraction(XRD,Rigaku D/max-2500PC)tests were carried out.The evolution of microstructure and texture during the compression,was examined by electron backscattered diffraction (EBSD) analyses on a scanning electron microscope (SEM,TESCAN MIRA3) equipped with a HKLEBSD system using a step size of 1.5 μm.The samples for EBSD mapping were mechanically ground and electrochemically polished in the AC2 electrolyte solution at 20 V for 90 s.The electroplishing process was conducted at −25 °C,and such lower temperature was controlled with the help of liquid nitrogen.The EBSD data were recorded and postprocessed using the Channel 5 software.

3.Results

3.1.Microstructure and texture evolution

The microstructure of sample ST and samples BT1-4 before and after annealing were shown in Figs.2 and 3,respectively.From Fig.2b-e,it is observed that a large number of twins were generated in all four bimodal textured samples.The twin bands developed in its parent grain were almost parallel to each other,and the twin volume fraction increased as the increasing of compression strain along the TD.Obviously,twins in samples BT1-BT4 disappeared and replaced by twin-free grains after annealing.The average grain sizes of the prepared fi e samples are measured as～23 μm,～23 μm,～25 μm,～25 μm and～26 um for ST,BT1,BT2,BT3,and BT4,respectively.

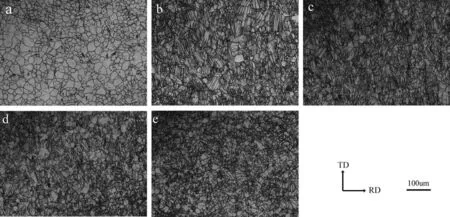
Fig.2.Microstructures of pre-deformed samples:(a) ST sample;(b) BT1 sample;(c) BT2 sample;(d) BT3 sample;(e) BT4 sample.

Fig.3.Microstructures of pre-deformed samples after annealing at 250 °C for 3 h:(a) ST sample;(b) BT1 sample;(c) BT2 sample;(d) BT3 sample;(e)BT4 sample.

Fig.4.Pole figure of pre-deformed samples determined by XRD:(a) ST sample;(b) BT1 sample;(c) BT2 sample;(d) BT3 sample;(e) BT4 sample.

Fig.5.Pole figure of pre-deformed samples after annealing at 250 °C for 3 h:(a) ST sample;(b) BT1 sample;(c) BT2 sample;(d) BT3 sample;(e) BT4 sample.

Pole figure of pre-deformed samples before and after annealing at 250 °C for 3 h were shown in Figs.4 and 5.The as-used ST sample exhibited a typical rolling texture with basal poles largely parallel to the ND and without preferred distribution of prismatic planes.For BT samples before annealing,there were two texture components with basal poles parallel to the ND (ND-texture) and with basal poles parallel to the TD (TD-texture).After annealing,the ND-texture exhibited a more scattering,while the type of texture hardly changed.Table 1 gives a statistical result for the fraction of TD-texture and ND-texture.The texture fraction was measured as the fractions of basal poles ± 30° around ND for ND-texture and ± 30° around the TD for TD-texture.Evidently,the fraction of TD-texture increased with a higher pre-strain along the TD.In BT4,the fraction for ND-texture is only approximately 10%,while that for TD-texture reaches approximately 73%.Here,the summed fraction of TD-texture and ND-texture was not 100%,because only the grain fraction with basal poles ± 30° around the TD and ± 30° around the ND were considered.Stanford et al.had reported that the compression along TD of the hot-rolled Mg alloys was mainly governed by the {102} twinning which will rotate the basal plane poles by about 86.3° toward the compression axis [14].Therefore,TD-texture component appeared after pre-compression along the TD.A higher pre-strain along the TD would lead to a higher twin fraction.A pre-rolling before the compression along the TD would increase the storage energy within twins,which contribute to recrystallization of twin structure.As shown in Fig.5,twins were disappeared and replaced by recrystallized grains,but the twin orientation were almost remained after annealing.Here,it was observed an increase of the sum fraction containing ND-texture and TD-texture of pre-deformed sample after annealing.It increases from 69% to 83% (Table 1) along with the amount of TD compression increases from 0% to 7%.The sum fractions counted after annealing have a close relation with that counted before annealing.The increase of this sum fraction is mainly because tensile twinning,though with slightly lower Schmid factor (SF) value,can occur in some grains from the remaining region with random texture (except ND/TDtexture) under TD compression.It will cause part basal poles toward to TD,and then decrease the remaining random texture and as well as increase the sum fractions of TD-texture and ND-texture.

Table 1 Fractions of TD-texture and ND-texture of pre-deformed sample before and after annealing at 250 °C for 3 h.

Table 2 Yield stress (YS),peak stress (PS) and elongation during tension and compression along TD of fi e types samples,respectively.

The evolution of microstructure during pre-deformation and subsequent annealing were further examined using EBSD and the results were shown in Fig.6.Many thick twins identifie as {102} twins were observed in BT2 (Fig.6c and d).The twins completely disappeared and the grains were refine after annealing.It could be seen in Fig.6e thatgrains with twin orientations (grain in blue and green) were observed.

3.2.Mechanical properties and tension-compression yield asymmetry

The true strain-stress curves under tension and compression along TD were plotted in Fig.7,with the relevant mechanical properties listed in Table 2.The fl w curve of ST in compression was characterized as a concave-up shape,which was regarded as a manifestation of {102} twinning predominant plastic deformation [34,35].The concave-up shape also appeared in the tensile curves of BT3 and BT4 samples.On the contrary,the stress-strain curve of ST sample under tension had a concave-down shape,typical feature of slip predominant deformation.This concave-down shape were also seen in curves of BT samples under tension.As seen in Table.2,ST sample had the highest yield strength under tension,while the lowest yield strength under compression.The tensile yield stress was much higher than the compressive yield stress in ST,and BT1,but an opposite tread was observed in BT3 and BT4.For BT2 sample,the tensile yield stress was similar to the compressive yield stress.To further understand the relationship between yield stress and bimodal textures,a rough linear relationship of yield stress changing with TD-texture fraction was established as shown in Fig.8:σb=161 −1.123VTD(under tension) andσb=75+0.6VTD(under compression).Under compression,the linear relation ofσb=75+0.6VTDworks well for BT samples.There is a relatively quick decrease of yield strength along with the increase of TD-texture component under tension,whereas a relatively slow increase of yielding stress along with the increase of TD-texture under compression.As a rough prediction of the linear relationship,there are acceptable deviations of yield stress for BT samples tested under tension,and the deviation decreases with the increase of TD-texture fraction.

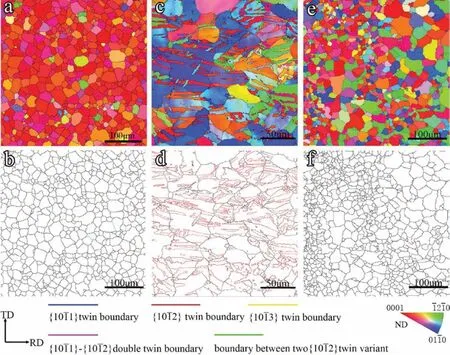
Fig.6.Inverse pole figur maps and the corresponding boundary misorientation maps:(a,b) ST sample after annealing at 250 °C for 3 h;BT2 sample (c,d) before annealing and (e,f) after annealing at 250 °C for 3 h.

The yield asymmetry distribution calculated as the ratio of compression yield strengthen (CYS) to tensile yield strength(TYS) was presented in Fig.9.The CYS/TYS was far from 1 for ST sample,indicating a strong yield asymmetry.All BT samples had a CYS/TYS closer to 1 than ST sample.In particular,BT2 sample showed the lowest asymmetry,and others deviated from 1 to some extent.For ST sample and BT4 sample,the ratio deviates from 1 a little bit more.The peak strengths,however,do not show the same tread as yield strength.For ST sample,unlike yield strength,the peak strength was not the highest under tension.The peak strength of BT sample under tension decreased in the rule of BT1,BT2,BT3 and BT4.Under compression,the peak strength didn’t show an obvious dependence on the bimodal texture.The elongation of ST sample is～14%,whereas there is a decrease of elongation of BT samples.The elongation of BT1,BT2,BT3 and BT4 are～11%,～10%,～9% and～8%,respectively.

4.Discussion

The results in this study strongly show that bimodal texture distribution in Mg alloy can pose a great effect on the tensioncompression yield asymmetry.From the classical Hall-Petch relationship [36]:σy=σ0+kd−1/2,yield strength is mainly determined by the yielding of the grain interior (σ0=Mτ0)and boundary obstacle effect (kd−1/2),whereMis the Taylor orientation factor andτ0the CRSS.Mcould be calculated as the reciprocal of the averaged SF (Schmid Factor).It means that the yielding of grain interior can be reflecte through the calculation of CRSS/SF.For samples with bimodal texture distribution,a different orientation will generate a difference in SF for slip/twinning.The effect of Schmid factor of deformation modes on the yield stress is not directly analyzed by the value of SF,but through the analysis of CRSS/SF.Generally,the slips or twinning with a higher SF and a resultant lowerσ0(i.e.CRSS/SF) is considered easily to be activated.For the boundary obstacle effect on slip,it is well understood in terms of dislocations pile-up in the vicinity of grain boundaries.The yielding happens when the pile-up of dislocations exerts sufficien stress at grain boundaries to initiate slip propagation from one grain to its neighbor [37].Twinning generally nucleates at grain boundary followed by a fast propagation and termination at the next grain boundary.The termination of a twin at grain boundary will generate a localized stress concentration at the twin tip,which would aid twinning nucleation in the next grain [38].Therefore,the contribution of boundary obstacle effect on yield strength is mainly related to its obstacle effect against slip/twinning transfer between neighboring grains.

Fig.7.Stress-strain curves under tension and compression along the TD of samples after annealing at 250 °C for 3 h.

Fig.8.A rough prediction of the linear relationship of yield stress changing as a function of TD-texture component,(a) under tension along the TD and (b)under compression along the TD.

The effect of grain orientations on slip/twinning transfer is generally realized by affecting the activation stress difference(Δstress) of slip/twinning and strain compatibility between neighboring grains.A lowerΔstressbenefit easier deformation transfer and the resultant lower boundary obstacle effect.Geometric compatibility factor (m＇) has been found to be an effective parameter to reflec this strain compatibility condition [39] and calculated using the equation below:

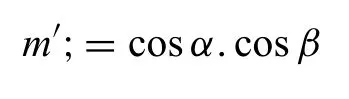
whereα/βis the angle between the slip (twinning) planes/slip (twinning) directions of two neighboring grains.A higherm＇indicates better strain compatibility and the resultant lower boundary obstacle effect.According to the above discussions,a compound analysis of activities of slip/twinning(yielding of the grain interior) and its transfer (boundary effect) in tension and compression could be well evaluated the bimodal texture effect on the yield asymmetry.

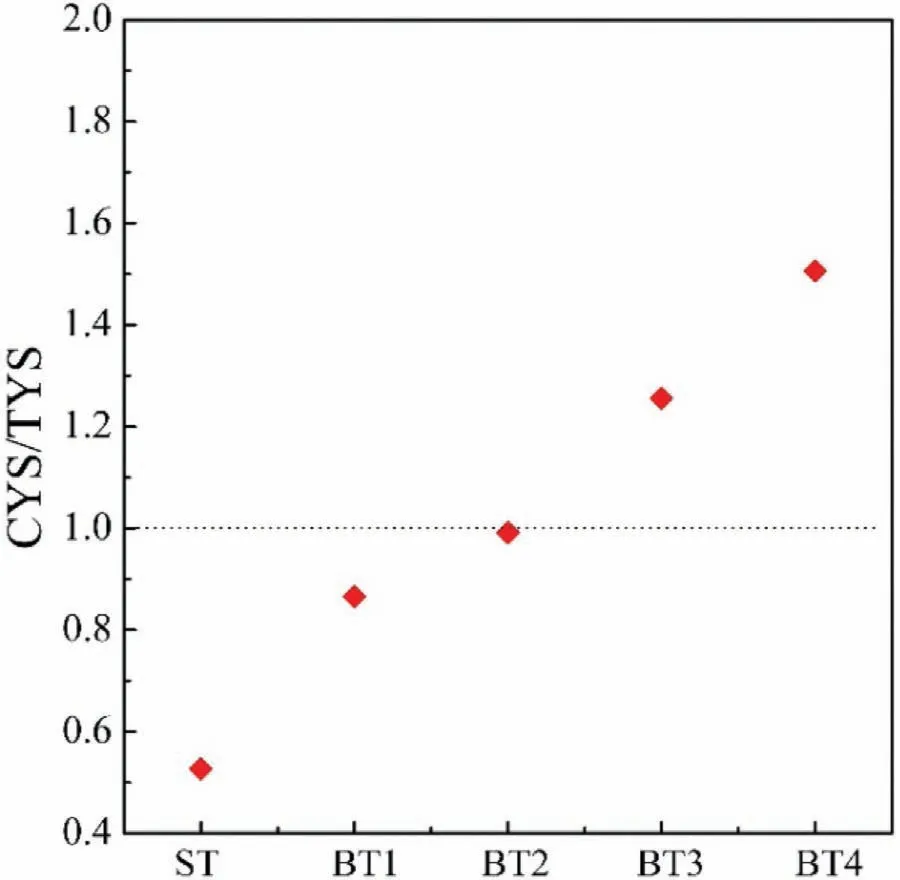
Fig.9.Ratio of CYS/TYS for different samples.

For the determination of active deformation mode and deformation transfer pairs under tension and compression,it mainly contains the following four steps:

Step i:extract the orientation information of each grain from the EBSD data:Euler angles

Step ii:calculate the value ofσ0(σ0=Mτ0=CRSS/SF)for each deformation modes like basal slip,prismatic slip,and {102} twinning assisted by the Matlab procedure.The Matlab procedure codes (a protected file contain the calculation of Schmid factor (SF) for each deformation mode.For uniaxial loading,the physical interpretation of the Schmid factor (SF) is rather clear and it is calculated asSF=cosφ× cosφ,whereφis the angle between the load axis and the slip/twinning plane normal andφis the angle between the loading axis and the slip/twinning shear direction [40].

Step iii:compare the above values calculated in step 2,and the deformation mode has the lowest value of CRSS/SF(lowest yielding of the grain interior) is determined as the dominant mode.

Step iv:after the determination of the dominant mode in a grain in step 3,for a pair of grains,if one is dominated by basal slip and the neighbor one is dominated by prismatic slip,then the B-P pair is allowed.If two neighbor grains are both dominated by{102}twinning,then the T-T pair is allowed,and it’s the same for the determination of B-B pair,B-T pair,and P-P pairs.

According to previous publications,the ND-texture favored{102} twinning under compression,but prismatic＜a＞slip under tension along the TD.In contrast,TD-texture was favorable for twinning under tension [5].Basal slip can also be easily activated in deformation as its lower CRSS (critical resolved shear stress) [41].In this study,the relative activity of basal slip,prismatic slip and {102} twinning in ST and BT samples under tension and compression were calculated.The results are listed in Table 3.The detailed examples and method to show how to determine the dominant deformation mode and transfer pairs were provided in the Supplementary Material.For each sample,approximately more than 400 grains were used in the calculation.As the more than 400 grains were selected randomly from each sample,the grains of the remaining region (except ND/TD-texture) have been considered for analysis of dominant deformation modes.The Euler angles of all the grains used in the calculation also provided in the Supplementary Material.The CRSS ratio for basal slip:prismatic slip:{102} twinning in polycrystal Mg alloys is a complex issue [42,43].Although,the CRSS ratio in single-crystal pure Mg has been successfully measured,this ratio could not be directly used in polycrystal Mg alloys.The calculation by Hutchinson et al.showed that the higher dislocation density and solute atoms in polycrystal Mg alloys could greatly reduce this ratio [44].For instance,the CRSS ratio of basal slip to prismatic slip in single-crystal pure Mg is approximately 1:40 [44],but this ratio is estimated to be 1:2-5 for polycrystal Mg alloys [45].The CRSS ratio of 1:1 for basal slip to twinning have been recognized as an effective ratio.According to the publication of S.R.Agnew and R.H.Wagoner [46],compared with the {102} twinning having a CRSS value twice that of basal in pure Mg,it appears that the addition of aluminum and zinc solutes raises the CRSS for all deformation mechanisms,as expected,and compresses the ratios among them.For example,the basal slip CRSS is in the range of 10-45 MPa while the CRSS range for {102}twinning is 15-35 MPa.Thus,basal slip and {102} twinning have roughly equal CRSS’s.Furthermore,according to the Schmid law [47]:

Table 3 Fractions of grains favoring basal slip,prismatic〈a〉slip,and{102}twinning under tension or compression along the TD of bimodal texture samples(BT1-BT4) and single texture sample (ST).The used CRSS ratio of basal slip:{102} twinning:prismatic slip is 1:1:3.

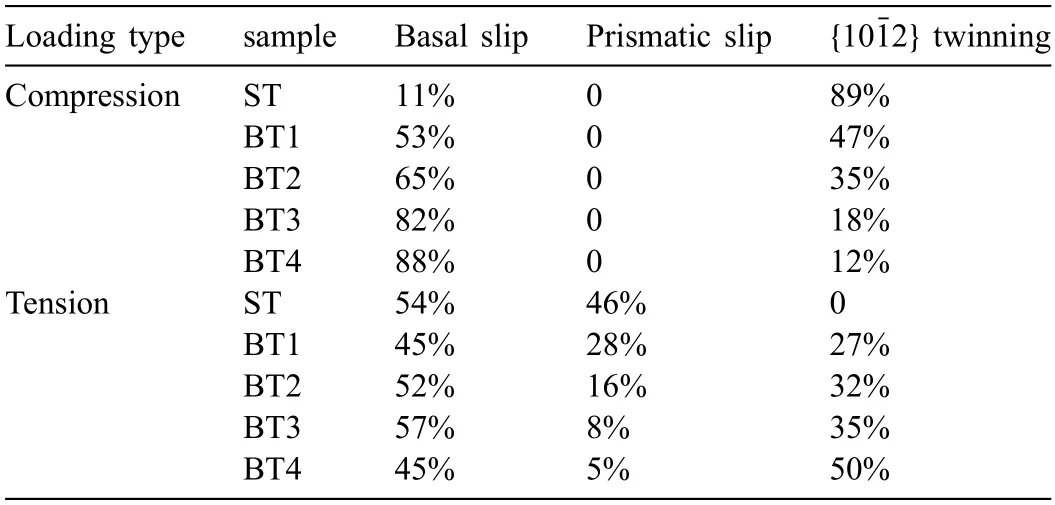
Table 3 Fractions of grains favoring basal slip,prismatic〈a〉slip,and{102}twinning under tension or compression along the TD of bimodal texture samples(BT1-BT4) and single texture sample (ST).The used CRSS ratio of basal slip:{102} twinning:prismatic slip is 1:1:3.

whereτis the resolved shear stress (CRSS) for basal slip or extension twinning,σis the applied stress for basal slip/extension twinning pre-dominated deformation andmis the Schmid factor;here,twinning is also assumed to respect the Schmid law [48].The experimental results indicate that the yielding stress (σbas.) of the basal slip pre-dominated deformation (grains with c-axes approximately aligned 45° to the tensile direction) is nearly the same with the yielding stress(σtw.) of {102} twinning pre-dominated deformation (grains with c-axes approximately aligned 0° to the tensile direction)[49].Furthermore,the Schmid factormfor basal slip and twinning are both higher and close to～0.5 in the above cases.Thus,it is deduced that the ratio ofτbasal/τtwinis roughly equal to 1:1.

Fig.10.Inverse pole figur maps showing the grains favoring different deformation modes under compression along the TD:(a) ST;(b) BT1;(c) BT2;(d)BT3 and (e) BT4.

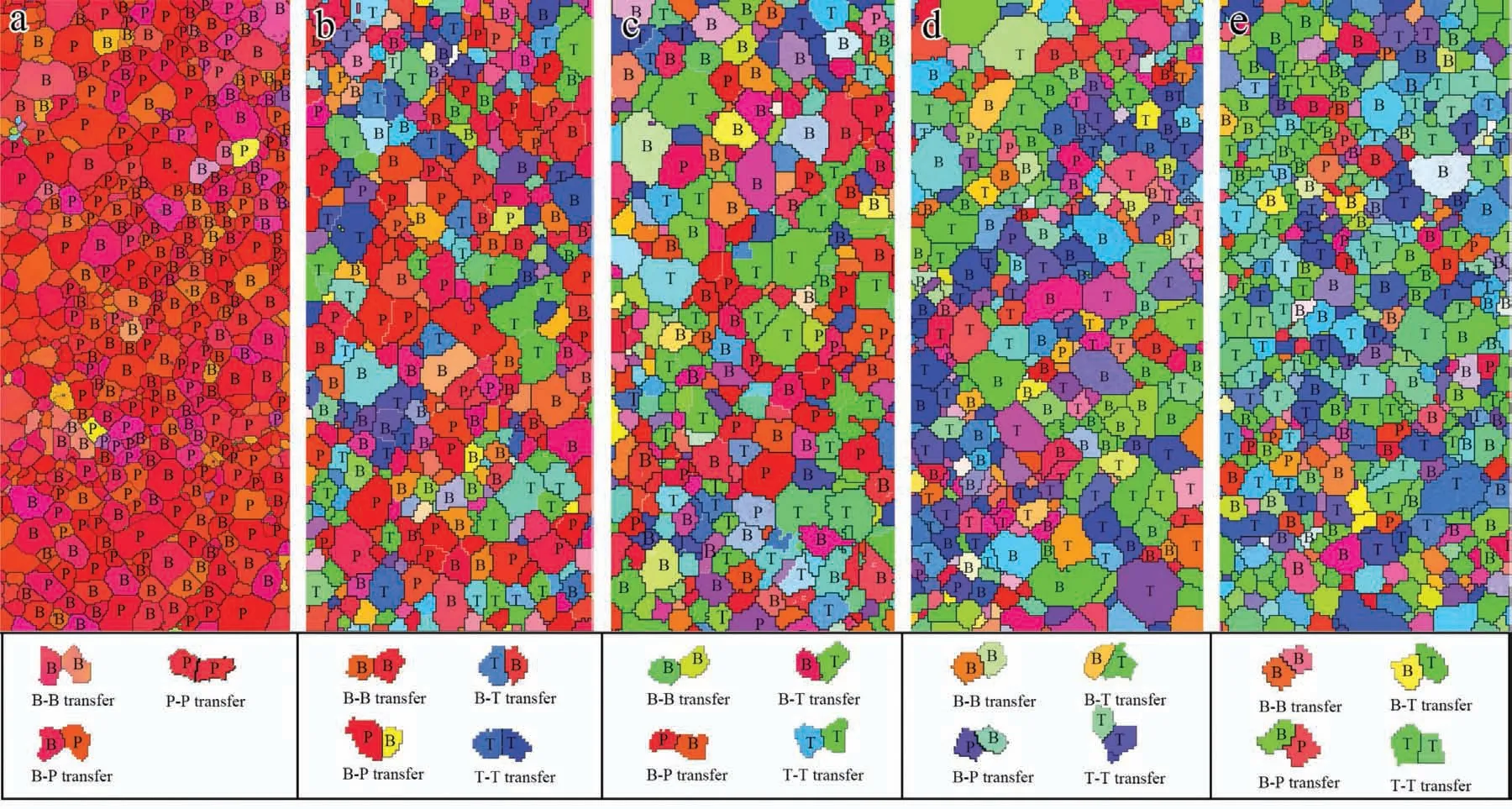
Fig.11.Inverse pole figur maps showing the grains favoring different deformation modes under tension along the TD:(a) ST;(b) BT1;(c) BT2;(d) BT3 and (e) BT4.

Considering this,a typical CRSS ratio of 1:3:1 for a basal slip,prismatic slip,and {102} twinning was used.Although pyramidal＜c+a＞slip might be initiated in Mg alloys,it cannot be activated in a large amount at room temperature or at a low strain.The yield strength in this study were measured at room temperature and at a 0.2% plastic strain.Therefore,pyramidal＜c+a＞slip is not considered in the calculations.

Fig.12.Distributions of ΔStress between neighboring grains under compression along the TD of (a) ST;(b) BT1;(c) BT2;(d) BT3 and (e) BT4 when B-B transfer,B-T transfer and T-T transfer are considered or when B-B transfer only,B-T transfer only and T-T transfer only are considered.

Under compression along TD,there is a higher fraction of{102}twinning occurred in ST(89%).The fraction of{102}twinning decreases in the order of ST,and BT1 to BT4.A large number of basal slip were initiated under compression in BT samples.Under tension along TD,except basal slip and {102} twinning,prismatic slip was occurred in BT samples.The data in Table 3 exhibit a general tread of decreasing prismatic slip activity and increasing {102} twinning activity along with increasing fraction of TD-texture under tension.The variations in slip activities and twinning activities quantifie for fi e samples indicate differences in their yielding of grain interior.An increasing activity of prismatic slip and a decreasing activity of {102} twinning may contribute to a higher yielding of grain interior.Interestingly,there is a similar activity of {102} twinning occurs in BT2 under tension(32%) and compression (35%),but it differs greatly in other samples,especially ST and BT4 samples.

Here back to the yield stress shown in Table 2,a higher yield strength of tension than that of compression in ST and BT1 is mainly related to the higher fraction of grains favoring prismatic slip which was initiated by a higher CRSS.Whereas,it is interesting to know why there is a higher compressive yield strength than tensile yield strength occurred in BT3 and BT4.As discussed previously,except the yielding of the grain interior,the boundary obstacle effect against slip/twinning transfer between neighboring grains also contribute to the yield strength.In this study,the grains favoring basal slip (labelled as B),prismatic slip (labelled as P) and{102}twinning(labelled as T)are marked in the inverse pole figur maps in Figs.10 and 11.It can be seen that B-B,T-T,B-T,and B-P transfers could largely take place under tension,and B-B,T-T and B-T transfers are three important transfer modes under compression.The fraction of each transfer was counted and also shown in Table 4.Because there is quite a low fraction of P-T and P-P in BT samples under tension,the fraction of P-T and P-P transfer do not have a statistical significanc and are not counted here.The distributions ofΔStressunder compression and tension along the TD are shown in Figs.12 and 13,respectively.TheΔStressin ST(2.97 MPa) under compression is much lower than that under tension (11.1 MPa).It’s the same tendency to BT1 sample.Whereas,there is a reversed tendency appeared in BT3 and BT4.TheΔStressin BT4 under compression is 11.3 MPa,but only 6.5 MPa under tension.There is a quite similarΔStressin BT2 under compression and tension.Figs.14 and 15 shows the distributions ofm＇under compression and tension,respectively.Them＇between each slip system (or twinning variant)is calculated from randomly selected 400 pairs of neighbored grains in EBSD data.As dislocations can glide in two opposite directions and a negativem＇means the influenc on dislocation gliding in the opposite direction,the maximum absolute value ofm＇is adopted to represent the strain compatibility for slip to slip and twinning to slip transfers.In stark contrast,twinning only allows shear in one direction,and a negative value ofm＇indicates a completely incompatibility.Therefore,the maximum value ofm＇is chosen for twinning to twinning.As seen in Figs.14 and 15,the average value ofm＇in ST and BT1 under compression (0.85 and 0.74) is higher than that under tension (0.63 and 0.68).In contrast,the value ofm＇in BT3 and BT4 under compression (0.71 and 0.73) is lower than that under tension (0.74 and 0.8).A lowerm＇and higherΔStresswould generate a higher boundary obstacle effect.

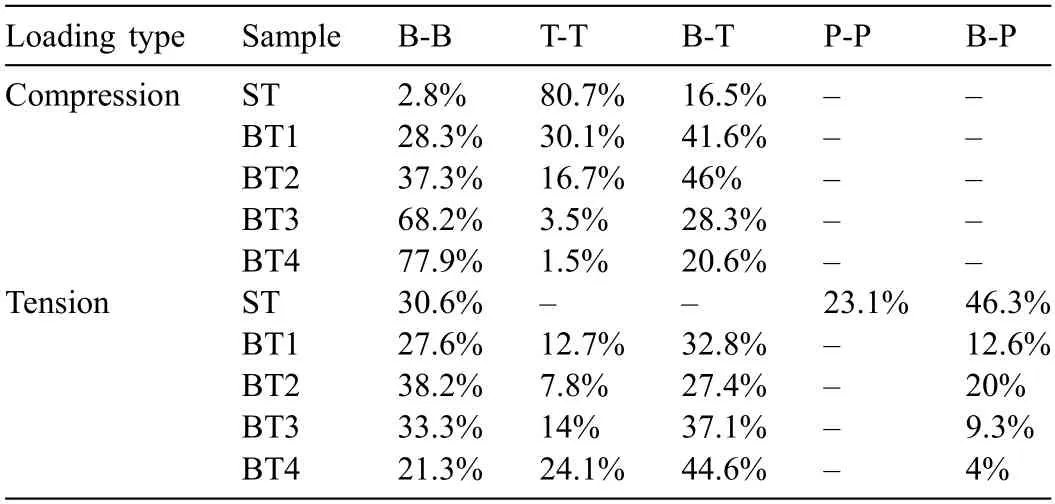
Table 4 Fractions of B-B,T-T,B-T,P-P,and B-P transfers during tension and compression along TD.

Fig.13.Distributions of ΔStress between neighboring grains under tension along the TD of (a) ST;(b) BT1;(c) BT2;(d) BT3 and (e) BT4 when B-B transfer,T-T transfer,B-T transfer (or P-P transfer) and B-P transfer are considered or when B-B transfer only,T-T transfer only,B-T transfer (or P-P transfer)only and B-P transfer only are considered.

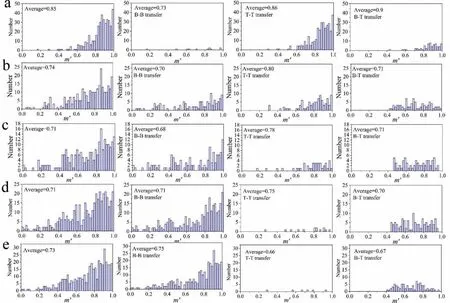
Fig.14.Distributions of geometrical compatibility factors (m＇) under compression along the TD of (a) ST;(b) BT1;(c) BT2;(d) BT3 and (e) BT4 when B-B transfer,T-T transfer and B-T transfer are considered or when B-B transfer only,T-T transfer only and B-T transfer only are considered.

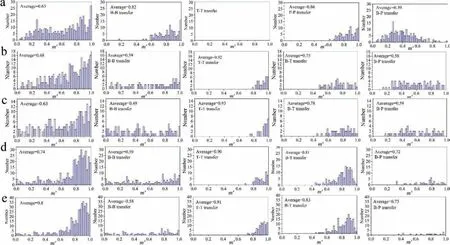
Fig.15.Distributions of geometrical compatibility factors (m＇) under Tension along the TD of (a) ST;(b) BT1;(c) BT2;(d) BT3 and (e) BT4 when B-B transfer,T-T transfer,B-T transfer (or P-P transfer) and B-P transfer are considered or when B-B transfer only,T-T transfer only,B-T transfer (or P-P transfer)only and B-P transfer only are considered.

Fig.16.Relative values of ΔStress/m＇ calculated during tension or compression along the TD of bimodal texture samples (BT1-BT4) and single texture sample(ST).The values in the figur is only a relative parameter to represent the boundary obstacle effect and isn’t represent the true value.

Therefore,the above results allow the reasons for the different bimodal texture dependence of tension-compression yield asymmetry to be well explained.The higher tensile yield strength than compressive strength in ST and BT1 is mainly related to their different activities of predominant slips and twinning,and a higher boundary obstacle effect generated under tension than that under compression further amplify the yielding differences.Resultantly,a remarkable yield asymmetry appeared in ST and BT1.There is also an obvious tension-compression asymmetry in BT3 and BT4.Under tension,although some grains favoring prismatic slip could increase the yielding of grain interior of BT3 and BT4,but the fraction of grains favoring prismatic is quite lower and the hardening effect is very limited.Besides,the relative lowerΔStressand higherm＇of BT3 and BT4 under tension causing a lower boundary obstacle effect than that under compression and the much higher compressive yield strength than tensile yield strength is the result.For BT2,even though there are some grains favoring prismatic slip under tension,but the hardening from hard orientations (ND-texture which favoring prismatic slip with higher CRSS) is limited when soft orientations (TD-texture which favoring {102} twinning with lower CRSS) are the majority (＞50%) [33].Why BT2 exhibit the lowest yield asymmetry is close related with their balanced {102} twinning activity (as discussed earlier) and similar boundary obstacle effect.Fig.16 shows the relative values ofΔStress/m＇under tension and compression to represent the boundary obstacle effect.A higher value ofΔStressor a lower value ofm＇indicates a higher boundary obstacle effect.Although,theΔStressunder compression(7.9 MPa)in BT2 is slightly higher than that under tension (7.5 MPa),them＇under compression (0.71) is also higher than that under tension (0.63).So there is a quite similar boundary obstacle effect observed in BT2.Furthermore,the gradually increasing trend ofΔStress/m＇values in ST,BT1,BT2,BT3 and BT4 under compression and gradually decreasing tread under tension is in highly consistent with the yield strength variation tread of ST,BT1-BT4 both in tension and compression.It proves that the contribution of grain boundary as a barrier impeding the deformation transfer is signifi cant,especially for alloys with bimodal texture components distribution.

5.Conclusion

This work provides an easy operated and economic way to weaken strong texture in AZ31 Mg alloy,and the quantifie relationship between tension-compression yield asymmetry and bimodal texture components distribution was established.The mechanism of the high dependence of yield asymmetry on the bimodal texture distribution was addressed,and the key finding are summarized as follows:

(1) Tailoring ND texture (c-axis// ND) and TD texture(c-axis// TD) distribution in Mg-3Al-1Zn plate is a highly effective way to improve the yield asymmetry,i.e.,CYS/TYS equal to 1 is obtained when two textures distribute at appropriate proportion:ND-texture account for～24% and TD-texture account for～55%.

(2) Analysis of the activities of slips/twinning and a compound use ofΔStressandm＇between two neighboring grains can clearly decipher this bimodal texture effect on tension-compression yield asymmetry.The occurrence of remarkable yield asymmetry in ST and BT1 is mainly related with a much higher activity of prismatic slip during tension versus a much higher activity of {102} twinning during compression.The higherΔStressand lowerm＇under tension stimulate a higher boundary hardening effect than that under compression,which further amplifie the yield strength differences between tension and compression;the good symmetry in BT2 is attributed to balanced twining activity and a quite similar boundary obstacle effect between tension and compression.

(3) The hardening effect induced by a lower fractions of prismatic slip activated during tension in BT3 and BT4 is very limited when the soft orientations (ND-texture＞50%) are the majority.A relative lowerΔStressand higherm＇of BT3 and BT4 under tension means an easier slip/twining transfer between neighbor grains than that under compression,which eventually leads to the lower boundary obstacle effect and thus a lower tensile yield strength than compressive yield strength.

Declaration of Competing Interest

The authors declare that they have no conflic of interest.

Acknowledgments

The current study is co-supported by National Natural Science Foundation of China(51901202,52101132),and Natural Science Foundation of Jiangsu Province (No.BK 20191442).

Supplementary materials

Supplementary material associated with this article can be found,in the online version,at doi:10.1016/j.jma.2022.03.002.