柔性薄壁轴承的周期性冲击背景特性及其分离

赵学智，叶邦彦，陈统坚

（华南理工大学机械与汽车工程学院，广东广州 510641）

引言

柔性薄壁轴承是谐波减速器的重要部件。谐波减速器具有传动比大、传动精度高、传动效率高、体积小等优点，被广泛应用于空间飞行器、工业机器人、雷达设备以及医疗设备等器械的传动系统中［1-2］。谐波减速器的核心元件之一是柔性薄壁轴承，与普通滚动轴承相比，柔性薄壁轴承内外圈的壁厚很薄且具有较大的韧性和弹性，这种轴承装配在椭圆凸轮上，内、外圈发生弹性变形成为椭圆，因此它是一个椭圆轴承。在谐波减速器中，柔性薄壁轴承的外圈上装有带外齿的柔轮，它与带有内齿的刚轮相啮合，当椭圆凸轮旋转时，凸轮周期性挤压柔性薄壁轴承以及柔轮，使得柔轮的外齿与刚轮的内齿周期性地啮合和脱开，实现将旋转运动从椭圆凸轮轴传递到刚轮［1-2］。柔轮的齿数比刚轮的齿数少两个，椭圆凸轮旋转一周，柔轮与刚轮的相对位移为其齿差所对应的角度，因此谐波减速器可以获得很高的单级减速比。

柔性薄壁轴承介于椭圆凸轮与柔轮之间，是谐波减速器传递动力的关键部件，它与普通滚动轴承的典型区别是：它的内、外圈是椭圆，这使得它的振动具有非常独特的特点。目前对于柔性薄壁轴承的研究主要是关于其疲劳寿命分析［3］、内外圈应力-应变以及载荷分布规律［4］、轴承结构参数对柔性轴承变形及应力的影响［5］以及轴承元件制造误差对柔性薄壁轴承和柔轮之间的应力影响［6］等方面的研究，而对这种轴承的振动分析和故障诊断的研究较少。目前只有Adams 等提出了一种椭圆轴承的有限元振动模型［7］，但是他们只是对椭圆轴承的振动进行有限元数值模拟分析，没有对此类轴承进行实际振动检测。笔者对这种特殊轴承的振动进行了实际检测和分析，结果表明Adams 等的这种有限元模拟分析结果并不准确。实际振动检测结果表明，在健康的柔性薄壁轴承的振动中，存在着一种周期性冲击，经研究发现这种冲击是由于椭圆长短轴的旋转造成的，这和普通滚动轴承完全不同，普通轴承只有在损伤后才会出现周期性冲击，而当柔性薄壁轴承损伤后，这种正常的周期性冲击和故障引起的周期性冲击混合在一起，形成一种复杂的冲击信号，对柔性薄壁轴承的故障周期性冲击特征是一个极大的干扰。本文分析了这种正常周期性冲击的频率分布特点，为了消除这种正常的周期性冲击对故障冲击特征提取的影响，提出利用奇异值分解方法将柔性薄壁轴承正常的周期性冲击从原始振动信号中分离出来，从而消除其对故障周期性冲击的干扰。在消除正常周期性冲击的影响后，采用连续Morlet 小波变换对故障周期性冲击进行提取，通过最大峭度确定最佳小波尺度。信号处理结果表明，SVD 能准确分离出柔性薄壁轴承振动信号中的正常周期性冲击，改善Morlet 小波对柔性薄壁轴承故障周期性冲击特征的提取效果。

1 实验装置和设备

针对柔性薄壁轴承的特点，设计了专门的柔性薄壁轴承振动检测试验台，其原理如图1所示，其中柔性薄壁轴承安装在高精度椭圆凸轮轴上。因为柔性薄壁轴承的内外圈都很薄，且有很大的韧性和弹性，装在椭圆凸轮轴上后，其内外圈发生弹性变形，被胀成椭圆。椭圆凸轮轴由电主轴驱动，其转速非常稳定。检测台还设计有径向力加载机构，便于在检测时对柔性薄壁轴承施加径向压力。PCB 加速度计安装在径向加载块上，振动信号由LMS 数据采集系统采集。试验台实物如图2所示。

图1 柔性薄壁轴承振动检测试验台原理Fig.1 Principle of vibration detection bench of flexible thinwall bearing

图2 柔性薄壁轴承振动检测试验台Fig.2 Vibration detection bench of flexible thin-wall bearing

本文实验中检测的柔性薄壁轴承型号为SHF-32-120，其主要参数如表1所示。

表1 型号为SHF-32-120 的柔性薄壁轴承参数Tab.1 Parameters of flexible thin-wall bearing with type SHF-32-120

2 健康柔性薄壁轴承周期性冲击特性

首先对一个健康柔性薄壁轴承的振动进行检测，检测时椭圆凸轮轴的转速为750 r/min，即转频为12.5 Hz，采样频率为6400 Hz，采样点数为4096点，检测到的振动加速度信号及其频谱如图3所示。

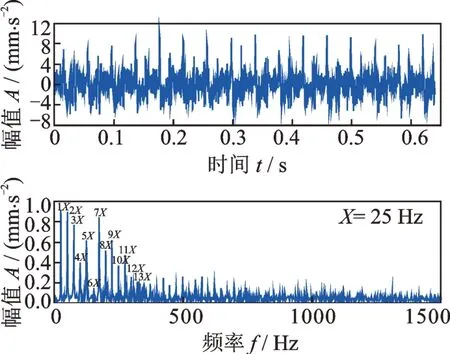
图3 健康柔性薄壁轴承的振动信号及其频谱Fig.3 Vibration signal of healthy flexible thin-wall bearing and its spectrum

从图3 可见振动信号中存在着非常明显的周期性冲击，但是需要注意的是：这是一个健康的柔性薄壁轴承。对于普通滚动轴承来说，只有在滚道或滚动体损伤后才会产生周期性冲击，健康的普通轴承振动信号中不存在周期性冲击，而图3 的结果表明，健康的柔性薄壁轴承中却存在周期性冲击，可见柔性薄壁轴承具有非常独特的振动特性，和普通滚动轴承完全不同。从图3 的频谱可见原信号在频域表现为一系列等间隔的频率成分。这种时、频域特征是周期性冲击的典型特征，对于理想的周期性冲击∑δ（t-nT）（其中T为冲击的周期），其在频域是一系列等间隔的谱线（1/T）∑δ（f-n/T）。因为这是健康的柔性薄壁轴承，因此把这种冲击称为柔性薄壁轴承的正常周期性冲击。由图3 可知，这种正常周期性冲击的基频是25 Hz，这正好是转频12.5 Hz 的两倍，而频谱中的其他频率是基频25 Hz 的一系列倍频，图3 中显示出了其1～13 阶的倍频。

正常周期性冲击的基频是转频的两倍这一现象不是偶然的，结合柔性薄壁轴承的特点，可知健康柔性薄壁轴承振动信号中的周期性冲击是椭圆的长、短轴造成的。因为柔性薄壁轴承内外圈是椭圆，随着内圈椭圆的旋转，椭圆长轴经过加速度计时，加速度计会受到一次向外的冲击，短轴经过加速度计时，加速度计会受到一次向内的冲击，方向与长轴的冲击方向相反。凸轮旋转一转，长轴经过加速度计两次，因此长轴引起的冲击频率是转频的两倍，短轴也经过加速度计两次，其引起的冲击频率也是转频的两倍。给出凸轮轴旋转一转时轴承受到的冲击，如图4所示（凸轮轴旋转一转的时间是1/12.5 Hz=0.08 s），可见在一转之内存在四个冲击，其中两个冲击是长轴引起的，两个冲击是短轴引起的，长轴和短轴引起的冲击方向相反，二者交替出现，其频率都是转频的两倍。在文献［7］中，Adams 等通过有限元数值模拟方法分析了椭圆轴承的振动，他们的模拟结果表明健康椭圆轴承的振动中存在正冲击和负冲击，这和本文作者的实测结果相符合，但是Adams等认为正冲击和负冲击的频率与圆形轴承的故障特征频率一致［7］，但作者的实测结果表明，健康椭圆轴承振动信号中正、负冲击的频率都是转频的两倍，这种实测结果表明文献［7］的有限元数值模拟结果并不准确。

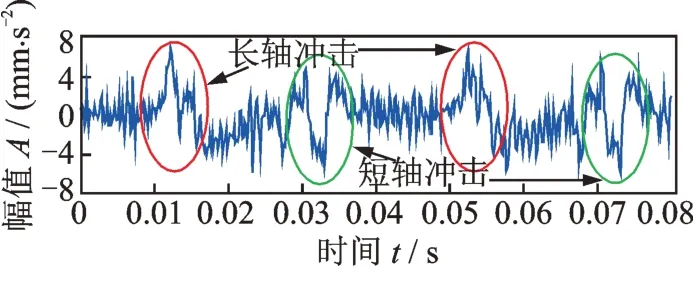
图4 凸轮轴旋转一转时柔性薄壁轴承受到的冲击Fig.4 Impacts on flexible thin-wall bearing when camshaft rotates one revolution

因为健康柔性薄壁轴承的振动信号中存在周期性冲击，而当柔性薄壁轴承损伤后，滚动体经过损伤点也会引起周期性冲击，正常周期性冲击和损伤周期性冲击混在一起，构成了一种非常复杂的冲击信号。对于普通滚动轴承而言，其内外圈是圆形，所以不会产生正常周期性冲击，不存在需要消除正常周期性冲击的问题，但柔性薄壁轴承完全不同，椭圆长短轴产生的正常周期性冲击较强烈，掩盖了损伤周期性冲击，因此在故障轴承的振动信号中必须设法消除这种正常周期性冲击。

3 SVD 分离正常周期性冲击的原理

奇异值分解是一种矩阵分解方法，近年来在信号消噪中有很多的应用。对一个实际采集到的柔性薄壁轴承振动信号［x（0），x（1），…，x（N-1）］，N为信号长度，为了对它进行奇异值分解，首先需利用这个振动信号构造如下矩阵［8-9］：

式中 1＜n＜N。令m=N-n+1，则H为一个m×n的矩阵，此矩阵又称为Hankel 矩阵［10-11］。对柔性薄壁轴承振动信号构造的矩阵H进行SVD 分解，得到：

式中U为一个m×m的单位正交矩阵，V为一个n×n的单位正交矩阵，D为一个m×n的对角矩阵。当m＜n时，D=[diag(σ1，σ2，…，σq)，0]；当m＞n时，D=[diag(σ1，σ2，…，σq)，0]T，0 表示零矩阵。q=min（m，n），且σ1≥σ2≥…≥σq≥0，它们是矩阵H的奇异值，也是信号x（i）的奇异值。

在信号处理中，SVD 一般是用来消噪的，SVD的消噪结果波形失真小，无相移，对机械振动信号［12-13］、磁共振信号［14］、生物医学信号［15-16］等不同性质的信号都有很好的消噪效果。但是SVD 除了消噪外，还可以提取原始信号中任意的单个或多个频率成分，这一特性源自于信号中频率和奇异值的一种内在联系［17］。由文［17］发现，利用原始信号x（i）构造Hankel 矩阵，当矩阵维数q大于原始信号中频率数量的两倍时，原始信号中的每一个频率成分将产生而且只产生两个非零奇异值，利用某个频率成分对应的两个非零奇异值进行SVD 重构，可以分离出这个频率成分［17］。在实际构造Hankel 矩阵时，对于确定的信号长度N，应使矩阵维数q最大［12］。由式（1）可见，原信号构造的Hankel 矩阵行数和列数存在约束关系m=N-n+1，当行数m增大时，列数n将变小，而矩阵维数q=min（m，n）。为了使q最大，如果信号长度N为偶数，取行数m=N/2+1、列数n=N/2 来构造Hankel 矩阵，此时q可取到最大值N/2；如果N为奇数，取行数m=（N+1）/2、列数n=（N+1）/2 来构造Hankel 矩阵，此时q可取到最大值（N+1）/2。实际处理信号的长度N一般至少为512，这样矩阵维数q至少为256，一般会大于原始信号中频率数量的两倍。

而为了分离出信号中一个具体的频率成分，必须选择出这个频率对应的两个奇异值。设原始信号x（i）是通过采样周期Ts得到的，对x（i）构造的m×n的Hankel 矩阵进行SVD 分解，设x（i）中的频率分量ajsin(ωjTsi+φj)对应的两个奇异值是σk和σk+1，可以证明，这两个奇异值的平方和与频率分量ωj的参数存在下面的关系：

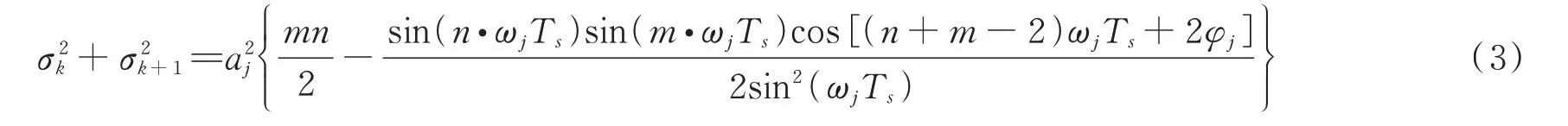
式中aj为频率ωj的幅值，φj为相位，m×n为矩阵阶数，Ts为原始信号的采样周期。对于确定的矩阵阶数和采样周期，由式（3）可见，频率分量ωj产生的两个奇异值的能量与ωj的幅值aj的平方成正比，幅值aj越大，则ωj对应的两个奇异值也越大，此外频率值ωj及相位φj也对奇异值的大小有一定影响，但幅值的影响是最大的［18］。在实际中，通过对x（i）做频谱分析，可以获得幅值aj、频率值ωj和相位φj，则可以利用式（3）计算频率分量ωj对应的两个奇异值的能量和。这样可以计算原始信号x（i）各个频率的奇异值能量和，因为奇异值序列是降序排列的，如果频率分量ωj的奇异值能量和在原始信号各个频率的奇异值能量和序列中排在第l位，则ωj对应的两个奇异值是σ2l-1和σ2l。将式（2）中正交矩阵U用列向量表示为U=（u1，u2，…，um），ui为m×1 的列向量，正交矩阵V用列向量表示为V=（v1，v2，…，vn），vi为n×1 的列向量，则选择奇异值σ2l-1和σ2l及矩阵U和V中对应的向量进行SVD 重构，可以得到：

从矩阵Hl中恢复出信号，它就是原始信号x（i）中的频率分量ωj。为了分离出多个频率成分，只需按照这样的方法选择这些频率对应的奇异值进行SVD 重构，就可从原信号中分离出它们。

因频率幅值对奇异值的影响是最大的，在实际中选取奇异值可采用一种比较简单的方法：一个频率产生两个非零奇异值［17］，而奇异值的大小主要是由频率的幅值决定的，幅值最大的前I个频率对应的奇异值一般是前2I个非零奇异值［18］。设原信号x（i）的频率总数是J，并且含有噪声，现需要从x（i）中分离出其中的I个频率，为了说明问题方便，以幅值最大的前I个频率的分离来说明。幅值最大的前I个频率对应的是前2I个非零奇异值，因此可将原始信号x（i）构造的矩阵H的SVD 分解分为三个部分，写成用列向量ui和vi表达的形式如下：

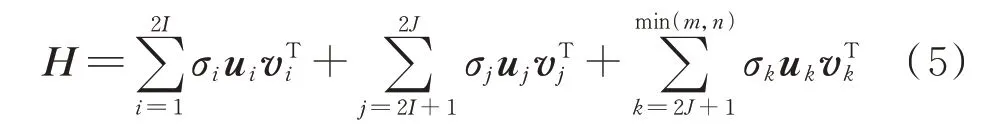
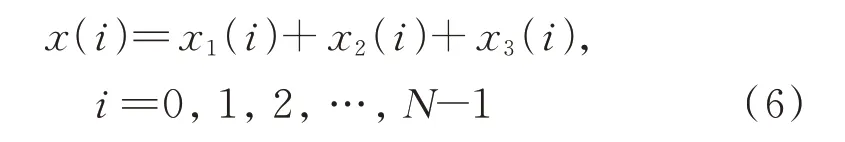
如果所需分离的I个频率的幅值并不是幅值最大的那几个，则只需利用式（3）计算每个频率对应的奇异值能量和，根据所需分离频率的奇异值能量和的大小顺序，选择相应的奇异值进行SVD 重构。通过这样的奇异值选择，得到重构矩阵共有2I个奇异值参与重构，从H1恢复的信号x1（i）就是所需分离的I个频率。

对于柔性薄壁轴承振动信号中的正常周期性冲击，从第2 节的分析可见它们的频率是以2 倍转频为基频的一系列倍频，根据这些频率的奇异值能量和的大小顺序，选择对应的奇异值进行SVD 重构，就可以从原始信号中分离出正常周期性冲击，从而消除它们对故障周期性冲击的影响。

4 故障冲击特征的Morlet 小波提取

消除了正常周期性冲击的干扰后，还必须进一步提取柔性薄壁轴承的故障周期性冲击。这种故障周期性冲击是快速衰减的调制冲击，提取这种调制冲击需要确定其调制频带，这是SVD 无法做到的。小波分析由于其良好的时频局部化分解特性［19］，可以用来实现这一目的。这里采用Morlet 小波来提取柔性薄壁轴承的故障周期性冲击，因为Morlet 小波的波形本身也是一个迅速衰减的调制冲击，它和轴承以及齿轮的故障冲击波形很相似，因而可以使故障冲击在Morlet 小波基上获得较大的投影，因此Morlet 小波很适合用来提取轴承和齿轮的故障周期性冲击特征信息［20-22］。Morlet 小波的表达式为：

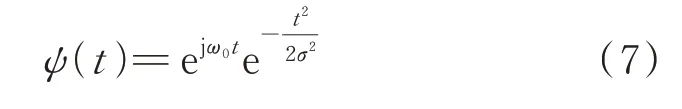
式中ω0为Morlet 小波的中心频率，σ为高斯函数的窗宽参数。连续Morlet 小波变换是信号x（t）和Morlet 小波在连续尺度s下的伸缩函数的卷积：

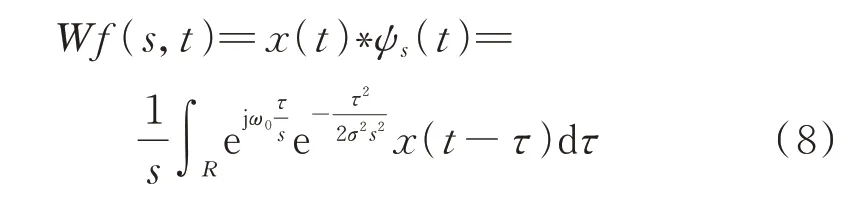
式（8）是模拟信号x（t）的连续Morlet 小波变换。对于采样得到的柔性薄壁轴承振动的离散数字信号x（i），其连续Morlet 小波变换是x（i）和小波基ψs(i)的数字卷积，如下式所示：

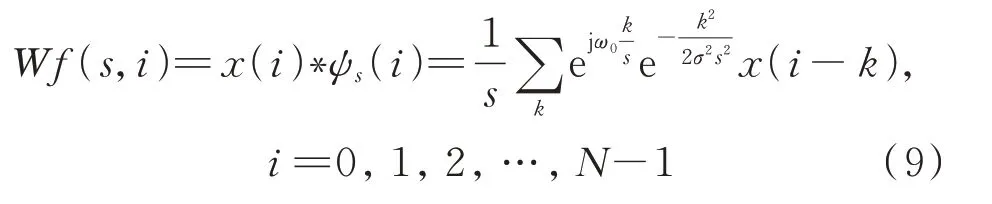
当尺度s连续变化时得到的一系列Wf（s，i）就是连续Morlet 小波变换的结果，尺度s和频率f具有一一对应关系，如下式所示：

式中fs为对原始信号x（t）的采样频率。

Morlet 小波尺度对柔性薄壁轴承的故障冲击特征提取结果有重要影响。不同尺度s下的Wf（s，i）反映了柔性薄壁轴承振动信号不同的细节特性，为了从一系列尺度下的Wf（s，i）中确定出含有柔性薄壁轴承故障冲击特征的尺度，可以通过计算各尺度下Wf（s，i）的峭度来解决这问题。峭度是一个对冲击信息比较敏感的参量，能够反映信号中的冲击特征［23-24］，如果某一个信号中含有冲击，则这个信号的峭度值会比较大［25-26］，峭度在旋转机械的故障诊断中有重要的应用。因此这里利用峭度来确定含有故障冲击特征的小波尺度，对于柔性薄壁轴承振动信号的连续Morlet 小波变换结果，尺度s下的Wf（s，i）的峭度按下式计算：

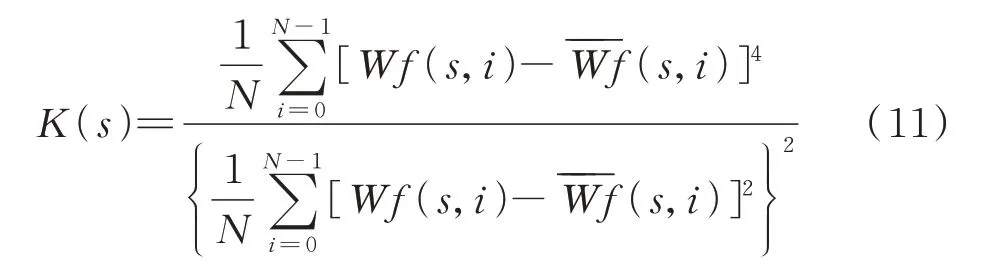
5 柔性薄壁轴承背景冲击消除实例

5.1 正常周期性冲击的SVD 分离

采用电火花加工对型号为SHF-32-120 的柔性薄壁轴承的外圈加工出一个深度和宽度都是1 mm的缺陷，如图5所示。从图5 可见柔性薄壁轴承的内外圈都非常薄，正是因为这种很薄的壁厚，使得这种轴承安装在椭圆凸轮轴上后很容易变形成为椭圆轴承，其参数如表1所示。在图2所示的振动测试系统上检测这个外圈损伤的柔性薄壁轴承的振动，检测时轴承转速及其他检测参数如表2所示。

图5 外圈损伤的柔性薄壁轴承Fig.5 Flexible thin-wall bearing with injured outer ring

表2 外圈损伤柔性薄壁轴承振动检测参数Tab.2 Vibration detection parameters of flexible thinwall bearing with damaged outer ring

检测得到的振动信号如图6所示。从图6 中可看到信号中有强烈的周期性冲击，但是这种冲击并非缺陷产生的故障冲击，而是椭圆长短轴产生的正常冲击。从图6 的频谱可见这个冲击是由以59.4 Hz 为基频的一系列倍频构成，59.4 Hz 正好是轴承转频29.7 Hz 的两倍，根据第2 节对健康柔性薄壁轴承的振动分析可知，这种以二倍转频为基频的周期性冲击是椭圆长短轴旋转产生的交替性冲击，并非缺陷产生的故障冲击。从图6 可见，这种正常周期性冲击很强烈，是柔性薄壁轴承振动的主要成分，缺陷产生的故障周期性冲击完全被这种正常周期性冲击掩盖了。普通滚动轴承是没有这种周期性冲击的，这种冲击是柔性薄壁轴承所特有的，它掩盖了故障周期性冲击，因此必须设法消除。

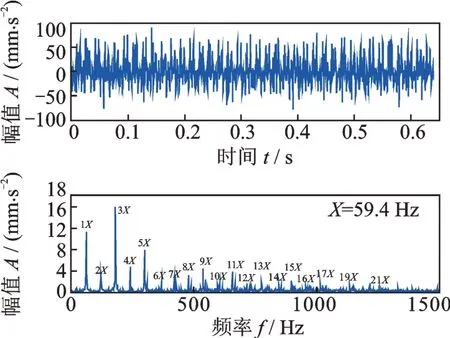
图6 外圈损伤柔性薄壁轴承的振动信号及其频谱Fig.6 Vibration signal of flexible thin-wall bearing with injured outer ring and its spectrum

现在用SVD 来分离这种正常周期性冲击。图6的原始信号长度是4096 点数据，因此利用原始信号构造一个2048×2049 的Hankel 矩阵并对其进行SVD 分解，得到正交矩阵U，V和奇异值对角矩阵D。从图6 可见，正常周期性冲击的频率是以59.4 Hz 为基频的一系列高次倍频，图6 的频谱中标识出了这些频率成分，它们分别是1～17 阶频率以及19和21 阶频率，一共有19 个频率分量。这些频率是频谱中的主要频率成分，它们的幅值在整个幅值谱中都是较大的。因为一个频率产生两个奇异值［17-18］，则19 个频率分量对应38 个奇异值。根据式（3）所示频率参数和奇异值大小的关系，选择出相应的38 个奇异值进行SVD 重构，然后采用平均法［27］从重构矩阵中恢复出信号，结果如图7所示。从图7 的时域波形可见提取到非常明显的周期性冲击，其频谱显示提取到的信号就是由以59.4 Hz 为基频的一系列倍频组成的，分别是1～17 阶频率以及19 和21 阶频率，共19 个频率分量，这和原始信号中正常周期性冲击的频率一致，而与故障周期性冲击无关，这表明原始信号中的正常周期性冲击成分被准确地分离出来了。还可以看到，分离出的周期性冲击的频谱中，两两相邻的谱线之间没有噪声频率存在，而且靠近冲击各个倍频的一些紧邻的谱线也没有混入进来，这是SVD 频率提取的一个优点。对于常规的滤波器而言，它通过设定频率范围进行频率提取，滤波器会把这个频率范围内的所有频率都提取出来，但SVD 是通过选择与每个频率相对应的奇异值来实现频率提取的，因此SVD 提取的频率不会有其他频率干扰。

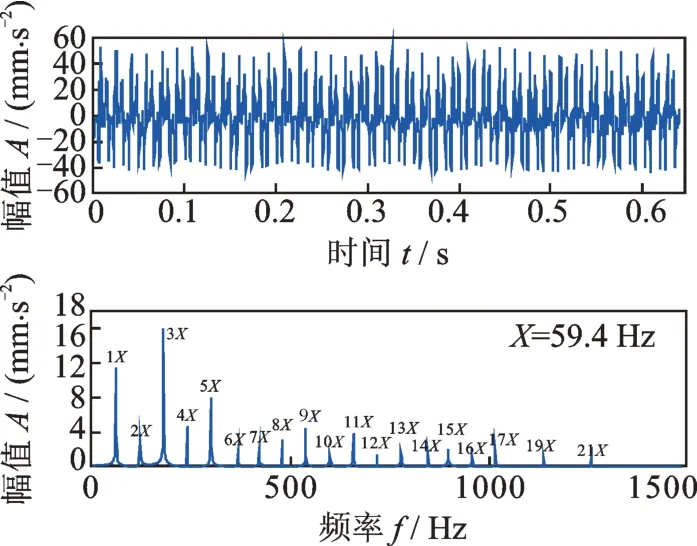
图7 SVD 提取到的正常周期性冲击背景信号及其频谱Fig.7 Normal periodic impulse background signal extracted by SVD and its spectrum

根据式（6），只需从原始信号中简单地减去所提取到的正常周期性冲击背景信号，就可以消除正常周期性冲击的干扰，这样得到的结果如图8所示。从图8 的频谱可见，在消除了正常的周期性冲击干扰后，此时频谱中已可观察到外圈故障特征频率307.8 Hz，但还是存在一些其他干扰频率，为了得到更准确的故障周期性冲击，还需要进一步提取故障冲击。

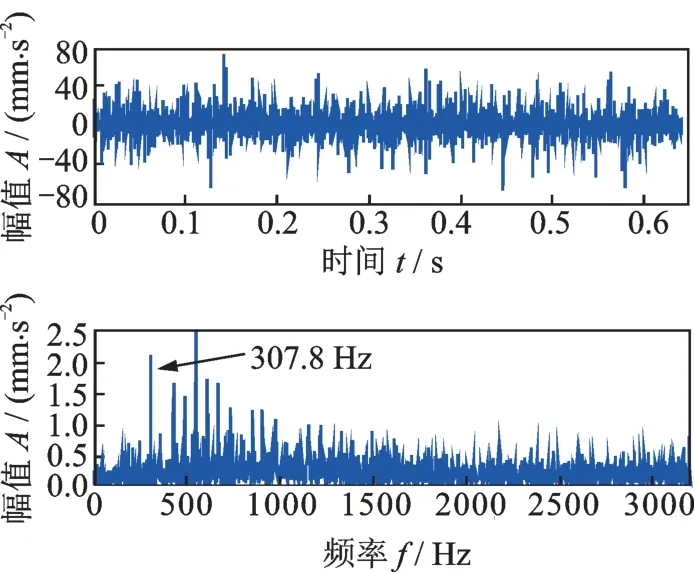
图8 消除了正常周期性冲击干扰的柔性薄壁轴承振动信号及其频谱Fig.8 Vibration signal of flexible thin-wall bearing in which the normal periodic impulses are eliminated and its spectrum

为了直观地观察正常周期性冲击的消除效果，给出内圈旋转一转时周期性冲击消除前后的振动信号对比（内圈旋转一转的时间是1/29.7 Hz=0.0337 s），如图9所示，可见一个旋转内由长轴引起的两个冲击和由短轴引起的两个冲击都已被针对性地消除了，冲击消除效果非常好。

图9 内圈旋转一转时正常周期性冲击消除前后振动信号对比Fig.9 Comparison of vibration signals before and after the normal periodic impulses are eliminated when the inner ring rotates one revolution

也可以采用滤波器方法来分离这种正常周期性冲击。从图6 中的原始信号频谱可见，正常周期性冲击的谐波分量主要是1～21 阶谐波，而第21 阶谐波的频率为21×59.4=1247.4 Hz，因此采用截止频率为1248 Hz 的低通滤波器来分离这种周期性冲击，结果如图10所示，可见也分离出了正常周期性冲击，但是和SVD 分离的正常周期性冲击相比（图7），滤波器分离出的正常周期性冲击的各阶谐波谱线之间还含有其他频率成分，这当中包括故障特征频率307.8 Hz，如图10所示。因此滤波器方法分离出的周期性冲击并不是纯粹的正常周期性冲击，部分故障特征信息也被分离出去了，故障特征信息有损失。而SVD 是利用频率分量和奇异值的内在联系点对点地将正常周期性冲击的各阶谐波分离出来，各阶谐波的谱线之间没有其他频率成分，也不含有故障特征频率（见图7），是纯粹的正常周期性冲击。

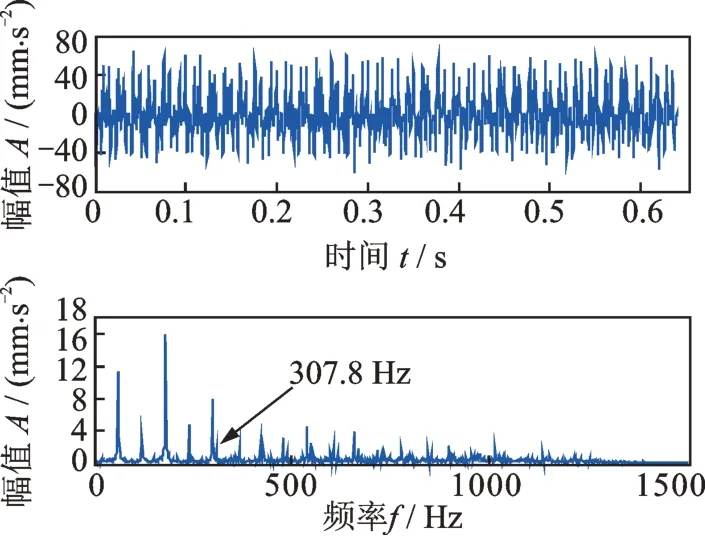
图10 滤波器分离出的正常周期性冲击背景信号及其频谱Fig.10 Normal periodic impulse background signal extracted by the low pass filter and its spectrum

采用滤波器方法消除了正常周期性冲击背景干扰后的振动信号如图11所示，从其频谱可见，前面一大频段的信息都已经完全被滤波器消除了，而故障特征频率307.8 Hz 却并没有在消除正常周期性冲击后显示出来。而利用SVD 方法消除正常周期性冲击得到的结果中（图8），只是准确地、点对点地消除了正常周期性冲击的各阶谐波频率，并不影响其他频率，其他频率信息包括故障特征信息依然还保留在信号中，此时故障特征频率307.8 Hz 已经显示出来了（见图8）。

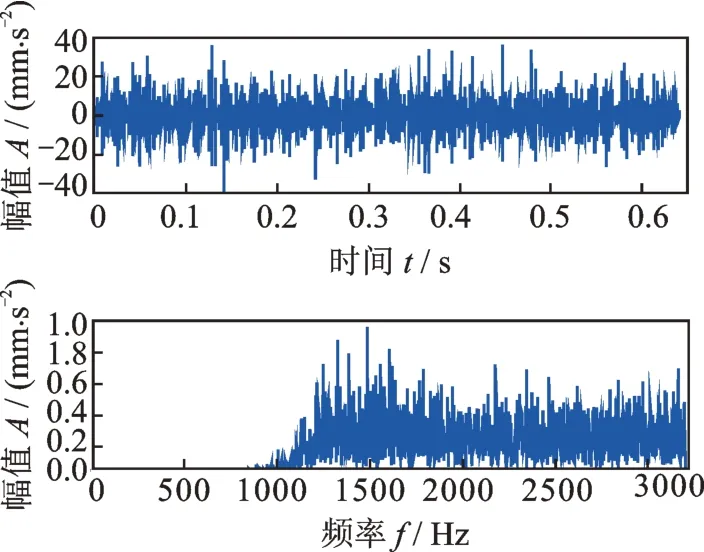
图11 利用滤波器方法消除了正常周期性冲击背景后的柔性薄壁轴承振动信号及其频谱Fig.11 Vibration signal of flexible thin-wall bearing in which the normal periodic impulses are eliminated by the filter method and its spectrum

5.2 故障周期性冲击特征的提取

利用连续Morlet 小波变换来提取柔性薄壁轴承的故障周期性冲击特征，连续Morlet 小波变换的尺度数是1024 个。首先，对于没有消除正常周期性冲击的原始振动信号、其连续Morlet 小波变换结果如图12所示，计算各个尺度的峭度，结果如图13所示，可见最大峭度位于第969 个尺度，峭度值为11.47，这个尺度的Morlet 小波变换结果如图14所示，其包络谱显示，外圈故障特征频率307.8 Hz 虽然被提取出来了，但是故障特征频率的高倍频并不明显，只有二倍频相对明显，并且故障特征频率基频及其二倍频周围还存在较多的频率干扰，如图14 中红色圈内所示，这些频率是正常周期性冲击产生的干扰频率。

图12 原始振动信号的连续Morlet 小波变换结果Fig.12 Continuous Morlet wavelet transform result of the original vibration signal

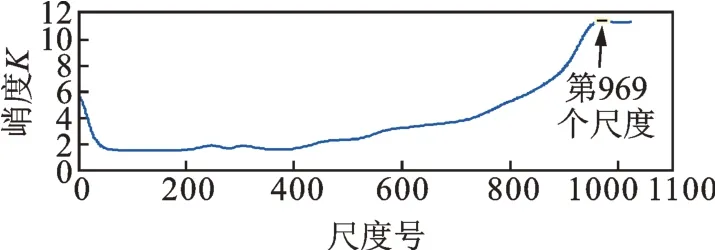
图13 原始振动信号的连续Morlet 小波变换各个尺度的峭度Fig.13 Kurtosis of continuous Morlet wavelet transform results of original vibration signal at various scales

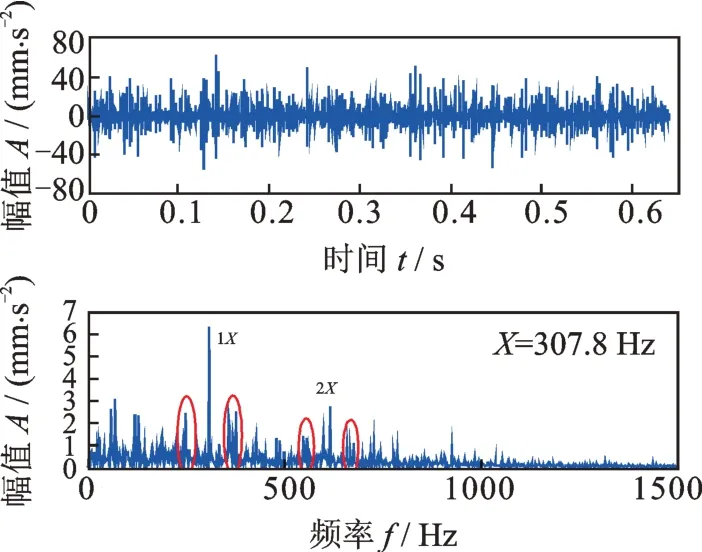
图14 未消除正常周期性冲击时提取到的故障特征Fig.14 Fault feature extracted when the normal periodic impulses are not eliminated

而对于消除了正常周期性冲击的振动信号，其连续Morlet 小波变换结果如图15所示，可见它和图12 的连续Morlet 小波变换结果存在明显区别。这种变换结果的各个尺度的峭度如图16所示，其中最大峭度位于第971 个尺度，其峭度值为11.32，这低于未消除正常周期性冲击时的最大峭度值11.47，分析其原因，是因为正常周期性冲击也会对峭度值产生贡献，当正常周期性冲击消除后，振动信号的峭度值就减小了。消除正常冲击后最大峭度值所在尺度的Morlet 小波变换结果如图17所示。

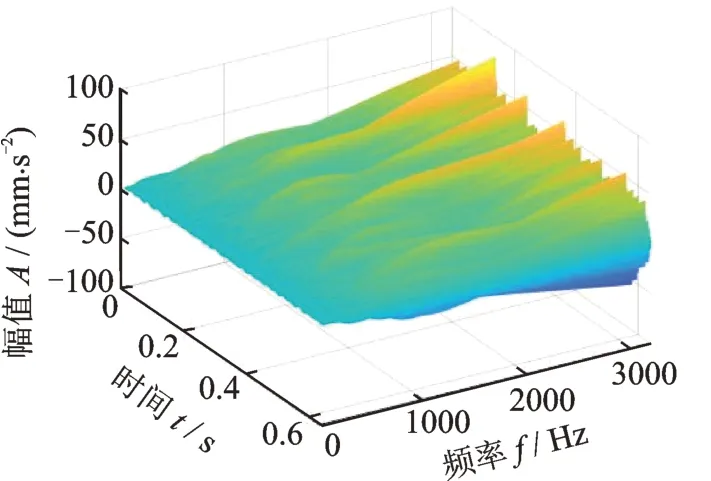
图15 消除正常周期性冲击后的连续Morlet 小波变换结果Fig.15 Continuous Morlet wavelet transform result after the normal periodic impulses are eliminated

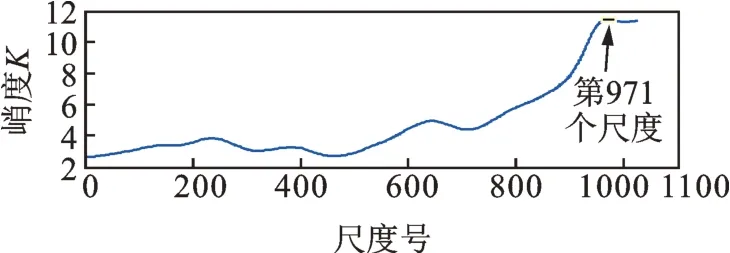
图16 消除正常周期性冲击后的连续Morlet 小波变换各尺度的峭度Fig.16 Kurtosis of continuous Morlet wavelet transform result at various scales after the normal periodic impulses are eliminated

图17 消除正常周期性冲击后的故障特征提取结果Fig.17 Fault feature extraction result after the normal periodic impulses are eliminated

和没有消除正常周期性冲击的包络谱相比（图14），可见图17 的包络谱中故障特征频率更加突出，故障特征频率307.8 Hz 时的2，3 和4 阶高倍频非常明显，并且故障特征频率及其倍频周围的干扰频率更少，而图14（b）中只有基频及2 倍频，其周围的干扰频率也较多。无论是正常周期性冲击还是故障周期性冲击，其在频域都是由基频和一系列倍频构成，倍频多，说明周期性冲击提取效果好。这可从正常周期性冲击的结果来说明（图7），它是很强烈的周期性冲击，其在频域内，基频及其倍频达到19 个（参见图7）。对于消除了正常周期性冲击的故障周期性冲击提取结果，其特征频率及其倍频比没有消除正常周期性冲击的特征频率及其倍频多。这种结果表明，在消除了正常周期性冲击的干扰后，柔性薄壁轴承的故障冲击特征被更加突出地显示出来了。

定义故障特征频率能量比率作为特征提取的定量评价指标，设所提取到的故障周期性冲击的包络谱用es（i）表示，i=0，1，2，…，int（N/2），N为原始信号长度，int（x）表示对x取整，不四舍五入，取int（N/2）是表示取包络谱的正频率部分即可，因为频谱是对称的。设包络谱中第k阶故障特征频率的幅值用ak表示，则故障特征频率的能量比率定义如下：

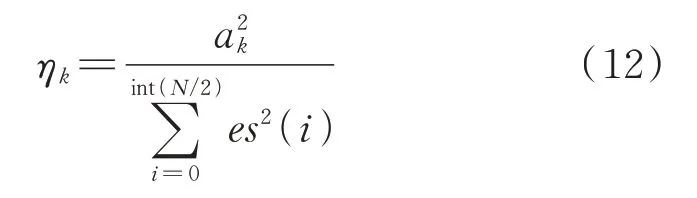
这个参数反映了所提取的故障特征频率的能量占总频谱能量的比例。对于消除了正常周期性冲击和未消除正常周期性冲击的振动信号，所提取的故障特征频率的能量比率如表3所示。可以看到消除正常周期性冲击后，故障特征频率的能量比率明显提高。

表3 故障特征频率的能量比率对比Tab.3 Comparison of energy ratio of fault feature frequency

6 结论

（1）柔性薄壁轴承的内外圈是椭圆，在轴承旋转时椭圆的长短轴会对轴承造成周期性冲击。内圈旋转一圈，长轴产生两个冲击，短轴也产生两个冲击，长、短轴产生的冲击方向相反，其频率都是转频的两倍。这种正常的周期性冲击掩盖了轴承元件缺陷引起的故障周期性冲击，使得柔性薄壁轴承的故障冲击特征不明显。

（2）正常周期性冲击的频率是柔性薄壁轴承振动的主要频率成分，利用奇异值和频率的内在联系，采用SVD 来分离柔性薄壁轴承的正常周期性冲击，选择正常周期性冲击的频率成分所对应的奇异值进行SVD 重构，就可从原始振动信号中分离出正常周期性冲击，实例结果表明SVD 分离出的正常周期性冲击波形清晰，无其他频率干扰。

（3）利用连续Morlet 小波变换对消除了正常周期性冲击的柔性薄壁轴承振动信号进行故障特征提取，并选择最大峭度对应的尺度为最佳特征尺度，实例分析结果表明，消除正常冲击后提取到的故障冲击特征频率更加清晰，其高倍频非常明显，干扰频率少，优于没有消除正常周期性冲击情况下的故障特征提取效果。