直流微电网并联储能系统改进下垂控制策略
张 晨,王啸尘,陈剑月,孙欣宇
(江苏大学 电气信息工程学院,镇江 212013)
为了推动实现可持续发展和节能减排目标,包含光伏、风电等清洁能源的微电网越来越受到关注[1]。与交流微网相比,直流微网与可再生能源之间的互连更加简单高效,直流系统中也不存在优化无功分布,抑制谐波等问题,因此更有发展优势[2]。在独立直流微网中,可再生能源具有随机性和波动性,需加入储能系统为负载提供不间断的电力[3-4]。为提高高功率水平分布式能源中储能侧变换器的可靠性,通常对变换器采取并联连接,其输出功率可按照要求进行扩展,同时并联变换器之间具有更快的动态响应速度[5]。当DC-DC 变换器并联运行时,各变换器之间功率是否平均分配,电压调节是否在规定范围内显得尤为重要。下垂控制是最常见的方法[6],其具有即插即用、无需高频通信等优点[7-8]。然而实际运行过程中,传统的下垂控制会因为系统线缆阻抗的存在和变换器的参数误差而出现功率分配不均及循环电流的现象[9],当流经某并行模块的电流较大时,不仅增大开关的损耗,还会使变换器过载[10]。为此,国内外学者展开了很多研究。
文献[11]为改善下垂控制参数采用虚拟阻抗方法,但需要在并网时获取信息得到虚拟阻抗,微电网无法孤岛运行。文献[12]通过注入微小脉冲电压的方式获取信息来改变下垂系数,但其误差会随着线路阻抗及等效电容的减小而放大。文献[13]以输出电流和母线电压变化率来改进下垂控制,但母线电压的稳定和储能系统之间电流的分配精度不能同时兼顾。文献[14]提出一种自适应下垂控制,通过PI 控制器自适应调节下垂参数,用另一个自适应PI控制器的次级环路调节直流微网总线电压,但它对通信要求很高。
上述的研究方法虽然能够改善线缆阻抗及变换器的参数误差对传统下垂策略带来的影响,但改进策略较繁琐、对通信要求高。为此,本文提出一种改进方法,以调节控制算法修改并联变换器电压设定点改善上述问题,该方法通过测量公共耦合点的电压、电流,就能满足并联系统对电压、电流的分配要求,无需在转换器之间建立通信。通过仿真和实验证明改进方法的有效性。
1 传统下垂控制策略
如图1所示,直流微网并联储能系统包含了储能单元、并联连接的变换器、线缆电阻、负载单元[15]。图1中:upcc为直流母线电压;Ii为变换器输出电流;usi为储能单元电压;Rci为线路阻抗;R 为负载;Iload为负载电流。并联变换器间采用下垂控制,通过给定的下垂参数可以控制储能系统之间的电流分配[16],传统下垂控制表达式为
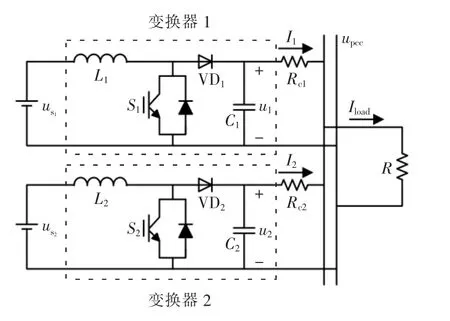
图1 并联储能系统结构简化图Fig.1 Simplified structure of parallel energy storage system

式中:ui为第i 台变换器端口实际电压;urefi为设定电压,Ii为下垂控制电流;Rdi为给定的下垂系数。
在小规模系统中,线路阻抗可忽略不计,由下垂参数进行功率分配[17],然而当直流微网规模很大时,电流分配的精度会因线路阻抗的存在而降低。考虑线路阻抗时,由图1可得:

联立式(1)和式(2),可求得电流分配的比例关系:

由式(3)可知,电流分配因为线路阻抗的不同而不同;且变换器的电感、电容等参数在实际运行中也会存在误差,加剧电流分配误差,使得变换器无法按照给定下垂参数进行功率分配。
2 改进下垂控制策略
2.1 阻抗误差消除控制算法
由上述分析可知,传统下垂控制方法中的均流效果由并联变换器的下垂系数决定,但线缆阻抗的存在会降低并联系统的电流分配精度和电压稳定性[18]。为消除线路阻抗所带来的影响,本文通过变换器耦合点的电流和负载电压信息,求得电压修正量,修正变换器的电压设定点,以此消除线路阻抗对传统下垂参数所造成的影响,提高了系统稳定性。求取电压修正量过程如下所示:
考虑线路阻抗时,电缆电阻会在公共耦合点改变下垂特性,负载电压可以用变换器1 或变换器2的输出电流表示如下:
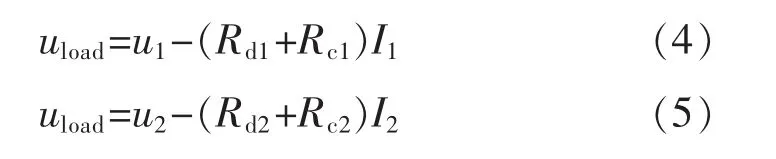
负载总电压uload和变换器电流Ii,线路阻抗R 关系如下:

将式(6)代入式(4)和式(5)可获得每个变换器的空载电压,将式(4)和式(5)改写如下:

通过求解式(7)和式(8),就可获得2 个并联变换器的输出电流估算值:
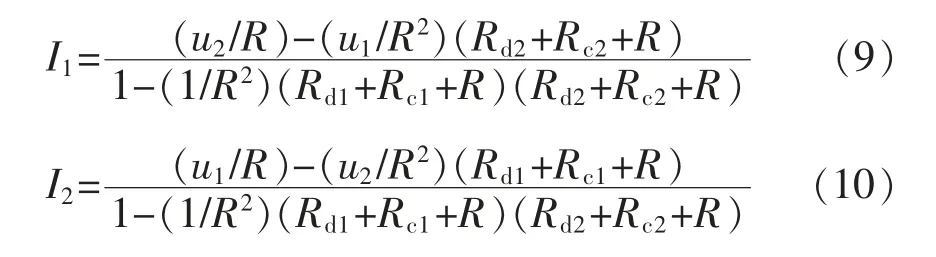
基于估算的变换器输出电流和负载电压值,可得到第i 个变换器的输出电压uoutput-i:

利用直流母线测得的额定电压值与第i 个变换器的估计输出电压值做差,求得电压修正量ΔV。因此,可通过ΔV 重新设定变换器的控制电压,使负载电流能够被每个变换器所共享,补偿电压下跌。图2为改进控制方法控制策略框图。

图2 控制策略对比框图Fig.2 Control strategy comparison block diagram
2.2 参数误差补偿控制算法
由2.1 节分析可知,线路阻抗造成的电流、电压误差可利用改变变换器在下垂控制中的电压设定点来消除。但实际运行过程中,变换器自身电感、电流等参数误差也会产生环流现象[19],为进一步精准分配电流,减小环流影响,对电流控制提出一种新的算法,通过将变换器和负载的电流值进行比较,将另一电压修正量加入控制环节,从而更好地提升电流分配的精度。
控制算法流程如图3所示,其作用是减小参数误差对变换器带来的影响,通过测量总负载和变换器的输出电流值,计算出第i 个变换器电流共享百分比PCS:


图3 控制算法流程Fig.3 Control algorithm flow chart
由于2 个并联变换器均分总负载的电流,所以并联时,第i 个变换器输出的电流值的大小应为总负载电流值的一半。因此,当第i 个变换器在输出电流占比高于一半时,需减小电压补偿量ΔuCA以降低电压设定值;相反,在输出电流占比低于一半时,变换器的电压设定值应增加ΔuCA的电压补偿量。通过上述算法可实现并联变换器之间电流的精确分配。但是,如图4所示,在实现电流均等共享的过程中,转换器的电流预设变化区间会在期望工作点附近产生较小的振荡现象。因此,必须选择适当的ΔuCA值以减小电流振荡对系统稳定性带来的影响。除此之外,当负载调节特性的下垂参数在转换器中表现较高时(即K>K′时),可实现所期望的工作点附近的振荡影响最小。

图4 不同下垂参数下期望点电流振荡Fig.4 Current oscillation at desired point under different droop parameters
本文中选择的ΔuCA较小,2 个下垂系数的取值在工作点附近产生的电流波形振荡也可忽略。所提的2 种控制算法同时使用时,通过对线路阻抗和参数误差进行分析,引入2 种电压设定点补偿法,有效地解决了电流分配过程中存在的问题,系统总控制框图如图5所示。
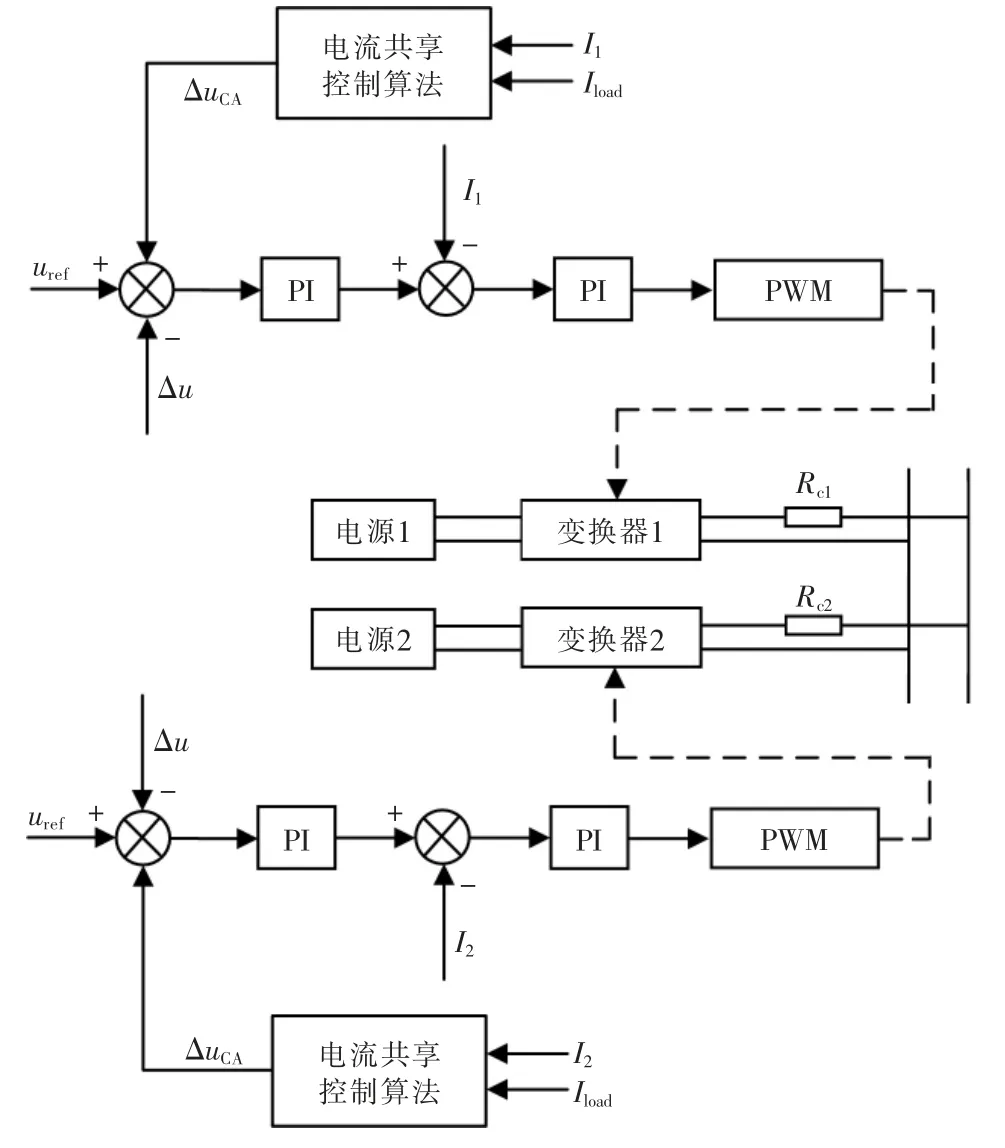
图5 系统总控制框图Fig.5 System total control block diagram
3 实验仿真验证
为了验证所提控制算法的有效性,图6所示在Matlab/Simulink 中搭建了光伏直流微电网并联储能系统模型,线路阻抗值采用被动检测法估计得到[20]。仿真采用的参数如下:光伏阵列工作在MPPT 模式下,固定输出电流40 A;直流母线额定电压为400 V;2个储能变换器采用相同下垂系数Rd=0.2,线路阻抗Rc1=0.2 Ω,线路阻抗Rc2=0.3 Ω;考虑到实际运行条件下相同变换器也会存在参数误差,设置变换器的参数不同,模拟实际使用时存在的情况,变换器输出电容C1=470 μF,C2=520 μF;变换器输入电感L1=0.5 mH,L2=0.6 mH;负载Rload1=50 Ω,负载Rload2=100 Ω,负载Rload3=150 Ω。

图6 直流微电网并联储能系统仿真模型Fig.6 Simulation model of parallel energy storage system in DC microgrid
3.1 阻抗误差消除算法验证
为了验证2.1 节所提控制算法的有效性,此实验将加入电压补偿改进控制算法的实验仿真和采用传统下垂控制方法的实验仿真进行了对比。实验中直流微电网设定为独立运行状态,负载在2 s 和4 s时发生波动,电流波形如图7和图8所示。
图7(a)为采用传统下垂控制方法的电流波形,在2 s 和4 s 时负荷发生波动,负荷功率由22.4 kW变为25.6 kW。传统下垂控制中,电流分配如下:开始时两DG 输出电流分别4.89 A 和3.06 A; 第一次负荷波动后输出电流分别为9.4 A 和6.2 A;第二次负荷波动后输出电流分别为14.3 A 和9.5 A,当负荷功率增大时,电流分配误差也会加大,进一步加剧环流,影响系统稳定。图7(b)为改进后的电流分配波形,可见电流误差显著减小。
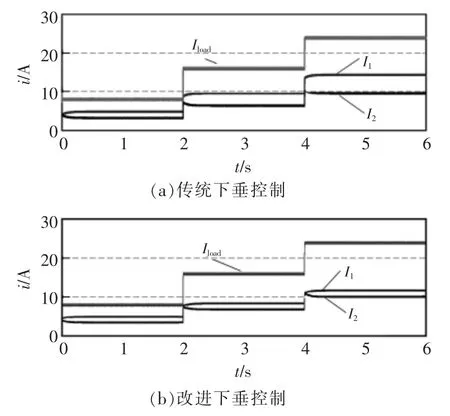
图7 两种控制方法电流波形仿真结果Fig.7 Two control methods current waveform simulation results
同时,如图8(a)所示,传统情况下母线电压在负载波动时分别跌落为395 V 和390 V,补偿量加入后,电压能够始终保持在400 V,保证了电压质量。

图8 两种控制方法电压波形仿真结果Fig.8 Two control methods voltage waveform simulation results
3.2 参数偏差补偿控制算法验证
上述阻抗误差控制算法考虑了线路阻抗的影响,仿真结果也表明,新的控制策略能抑制循环电流,电压降落问题也得到了解决。但图8(b)中,电流分配偏差没有能够完全消除,这是由于未考虑变换器参数偏差对控制造成的影响。为了验证2.2 节中参数偏差补偿方法的有效性,设定了2 个变换器参数误差,图9为加入电流算法后的电流波形。

图9 加入误差补偿的改进控制仿真结果Fig.9 Improved control simulation results with error compensation
由于本地通信网络下,变换器输出电流与负载电流信息实时传递,使得系统不断调整ΔuCA的值,修正电压最终达到了理想电压设定值。仿真波形显示,在负荷频繁波动时,阻抗和变换器参数对系统造成的影响完全消除,输出电流在每次波动后0.2 s左右就能实现精确分配。
3.3 实验验证
为了验证直流微电网并联储能系统改进下垂控制有效性,建立了储能系统半实物仿真平台。包括了2 组蓄电池来充当储能单元,dSPACE,2 台升压变换器,以及负载等元件。实验中变换器参数、线路阻抗参数、负载参数与仿真保持不变。实验时在25 s 切换负载,模拟负载波动情况,图10为实验波形。
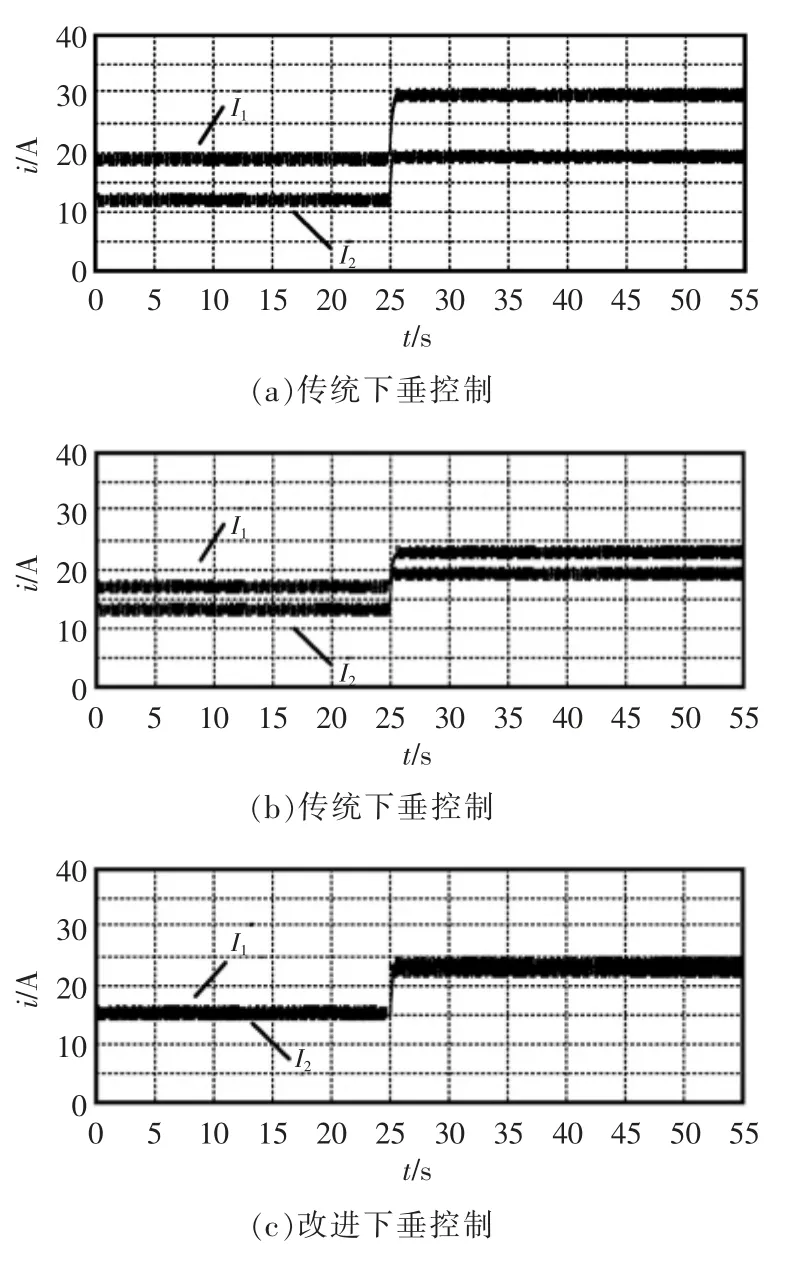
图10 实验波形Fig.10 Experimental waveform
从图10(a)可以看出,传统控制下,电流分配存在差异,并且随着负载的波动,变换器间产生的电流误差会加大,对系统的稳定运行造成影响,容易造成变换器的过载。图10(b)为考虑阻抗补偿的改进控制电流波形,负载波动时循环电流显著减小,但还没有完全达到要求。图10(c)为加入参数误差补偿的电流波形,可以看出利用本文提出的控制策略,达到了系统功率分配要求,证明了方法的有效性。
4 结语
针对直流微电网中并联储能系统采用传统电压-电流下垂控制方式时,线路阻抗和变换器参数误差造成的循环电流和母线电压波动问题。本文提出了一种用于改善并联变换器负载电流共享的控制方法。消除阻抗影响的算法基于公共耦合点的变换器电流和负载电压信息,修改了每个变换器的电压设定点,且无需在并联储能单元之间建立通信链接;参数偏差消除算法通过PSC 循环控制回路,利用每个变换器的电流与总负载电流的均流百分比与设定值比较,最终确定了电压设定值,确保了精确的负载电流共享和母线电压稳定。仿真和实验结果验证了所提出的改进控制算法的有效性。

