水下爆炸荷载下围压对岩石裂纹扩展影响的数值模拟
余 庆, 张 辉, 蔡志翔
(中国石油大学(北京)石油工程学院,北京 102249)
低渗透油气藏往往存在着渗透性差,产能低、开采难度大等问题[1-2],这就要求必须进行油气藏改造才能维持正常作业。常用的改造方式有水力压裂、高能气体压裂、“层间爆炸”压裂等[3-5],其中爆炸压裂是改造低渗透油气藏的潜在技术手段,通过井眼内炸药爆炸产生的能量对井壁围岩造缝,进而达到改善低渗透储集层物性、提高油气采收率的目的。井眼中炸药爆炸荷载对井壁岩石的破坏主要是爆炸激波和气泡脉动压力[6]共同作用的结果。由于二者对岩石的破坏机制以及作用时间尺度的不同,同时研究比较困难,所以本文中主要聚焦于水中爆炸激波对岩石的破坏作用,忽略气泡脉动的影响。前人对水中爆炸激波对岩石破坏效果做了大量工作,从载荷的施加方式、炸药与岩石是否接触、试样尺寸等多方面利用实验和数模方法得到了丰硕成果[7-11],然而鲜有看到围压对水下爆炸激波作用下岩石裂缝扩展的影响研究。围压对岩石裂缝扩展的影响研究,爆炸环境也主要发生在陆地上,如地下隧道、洞室钻爆开挖等[12-15],鲜有水中爆炸载荷对含围压岩石的损伤破坏研究。笔者基于水下爆炸理论,采用动力学分析软件LS-DYNA和后处理软件LS-PREPOST联合仿真,模拟无限水域水下爆炸冲击波的传播过程,冲击波对岩石的破坏过程,研究围压对水下爆炸荷载下岩石裂缝扩展的影响,为实际爆炸压裂和低渗油藏开发提供参考。
1 计算模型与参数
1.1 模型的建立
研究无限水介质中爆炸问题,模型轴对称,建模时取1/4模型,建模过程中统一采用cm、g、μs单位制。计算模型中水采用欧拉网格建模,炸药通过初始体积分数的方式添加到水域中,单元使用多物质ALE算法;位于炸药下方7 cm的岩石采用拉格朗日网格建模,单元网格附着在材料模型上,能较好实现单元质点的变形和位移过程;为了详细分析岩石的破坏损伤情况,采用侵蚀算法描述岩石的破坏损伤情况,本文中计算设置的最大失效主应变为0.002[16];水与岩石之间采用流固耦合算法,水与岩石的几何型和网格重叠在一起,计算中通过罚函数的方式将水与岩石耦合在一起以实现力学参量的传递。整个模型尺寸:水域的尺寸为15 cm×15 cm×40 cm,网格边长为0.3 cm;岩石的尺寸为5 cm×5 cm×5 cm,由于需要观察岩石破坏情况,也就有必要将岩石的网格画得比水更密,岩石的网格边长为0.1 cm;球形TNT炸药的质量为1.6 g。考虑到模型的对称性,在模型的对称面上设置对称边界条件,水的四周设置无反射边界条件,岩石的下表面与对称面施加法向约束,岩石的H面、h面和v面分别施加σH、σh、σv的围压;水和炸药构成的ALE域单元数量为332 500个,岩石单元数量为125 000个。
由于井下岩石受到围压的作用,在分析岩石受到水下爆炸载荷作用时,需要给模型施加初始应力,因此岩石受水下爆炸载荷作用下的裂纹扩展涉及动静耦合计算。采用LS-DYNA中的隐-显连续求解的方法实现预应力施加与爆炸荷载的耦合作用。采用隐式分析对岩石施加初始围压,然后再进行显式分析模拟水下爆炸对岩石的动载作用[17]。为了简化模型,模拟过程忽略井下静水压力对炸药的影响。计算模型如图1所示。
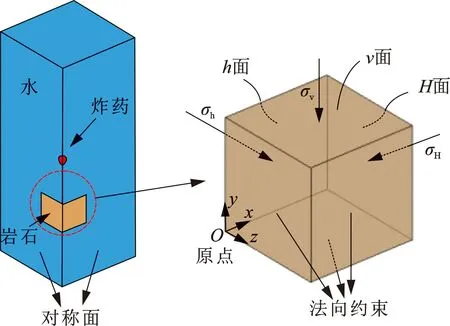
图1 计算模型示意图
1.2 材料模型及参数
TNT炸药采用Mat_High_Explosive_Burn材料模型和JWL状态方程[18],状态方程为
(1)
其中
A=371 GPa,B=7.43 GPa,R1=4.15,
R2=0.95,ω=0.3,E0=7 GJ/m3.
式中,p为爆轰产物的压力;V为比容(即单位体积装药产生的爆轰产物的体积);E0为单位体积的内能;A、B、R1、R2、ω为JWL状态方程常数。
水采用空物质材料本构模型和GRUNEISEN状态方程,水冲击压缩时方程为
(2)
其中
ρ0=1 020 kg/m3,C=1 484 m/s,S1=1.979,S2=0,
S3=0,γ0=0.11.
式中,C为声速;ρ0为初始密度;S1、S2、S3为试验拟合系数;γ0为GRUNEISEN状态方程参数。
水膨胀过程状态方程为
p=ρ0C2μ+(γ0+αμ)E0.
(3)
其中
α=3,E0=0,μ=ρ/ρ0-1.
式中,α为对一阶体积的修正。
岩石采用Johnson-Holmquist-Concrete(HJC)材料模型。该模型主要应用于冲击爆炸作用下混凝土类材料的动态响应中,综合考虑大应变、高应变率和高压效应,并且考虑损伤及损伤积累,是一种适合模拟爆炸冲击作用下的动态本构模型。以归一化等效应力描述HJC强度模型,具体表达式为
(4)
其中
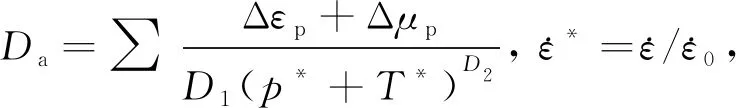
p*=p/fc,T*=T/fc.
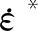
HJC模型的状态方程描述为
(5)
式中,Ke为体积模量;pcrush和μcrush分别为弹性极限静水压力和对应的体积应变;plock为压实静水压力;μlock为对应体积应变;K1、K2、K3为压力常数。
模型的具体参数[19]如下:ρrock=2.5 g/cm3,A=0.93,B=1.6,C=0.008,N=0.79,fc=61 MPa,Smax=7 MPa,D1=0.04,D2=1.0,Emin=0.004,pcrush=20.3 MPa,μcrush=6.6×10-4,K1=85 GPa,K2=-171 GPa,K3=208 GPa,plock=1.0 GPa,μlock=0.072,T=4.84 MPa。
2 仿真结果分析
将所建立的模型参数及有限元模型导入到LS-DYNA中进行求解运算,最后在LS-PREPOST中显示求解结果。
2.1 水下爆炸冲击波传播过程
在大量理论与试验的基础上,前人总结了一些水下爆炸冲击波传播参数的计算模型,其中Cole等[20]、Zamyshlyaev[21]关于无限水中爆炸激波的峰值压力经验公式应用较广,表达式为
(6)
式中,R为炸药中心距离测点的距离,m;Q为炸药质量,kg;pm为冲击波峰值压力,MPa;R0为炸药包半径。
图2为距炸药中心不同位置处的水下爆炸冲击波压力。从图2(b)中可以看到,冲击波压力在距离炸药中心3 cm处峰值压力达到330 MPa,随后迅速衰减到102 MPa (R=7 cm),传播到R=15 cm时,峰值压力仅为37.2 MPa。说明随着冲击波的传播,其波阵面压力和速度下降很快,且波形不断拉宽,在离爆炸中心较近处压力下降非常快,而离爆炸中心较远处压力下降较为缓慢。从图2(c)可以看出,数值模拟结果与经验公式得到的结果十分吻合,表明水中爆炸冲击波作用的计算模型和参数可信,计算结果正确,可以用于分析水中爆炸冲击波对岩石的破坏效果。
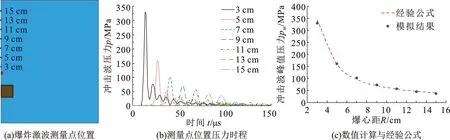
图2 距炸药中心不同位置处的水下爆炸冲击波压力
图3为炸药距离岩石为7 cm时爆炸冲击波的传播过程。从图3中可以看出,炸药爆炸后在流速为零的均匀水介质中形成的冲击波以球面的形式向外传播。当t=35 μs时,水中爆炸冲击波的波阵面清晰而狭窄,并传播到岩石的上表面,在岩石上表面发生透射和反射;当t=50 μs时,爆炸冲击波一部分透射进入岩石,一部分被岩石上表面反射;当t=66 μs时,激波从岩石进入水中,在岩石的侧面处同样发生反射与透射,由于岩石的声抗大于水的声抗,会向岩石内部反射拉伸波,向水中透射压缩波;当t=100 μs时,冲击波已经透过岩石,继续向外传播,但下半部分激波的压力明显小于上半部分,原因是岩石吸收了部分冲击波能量。
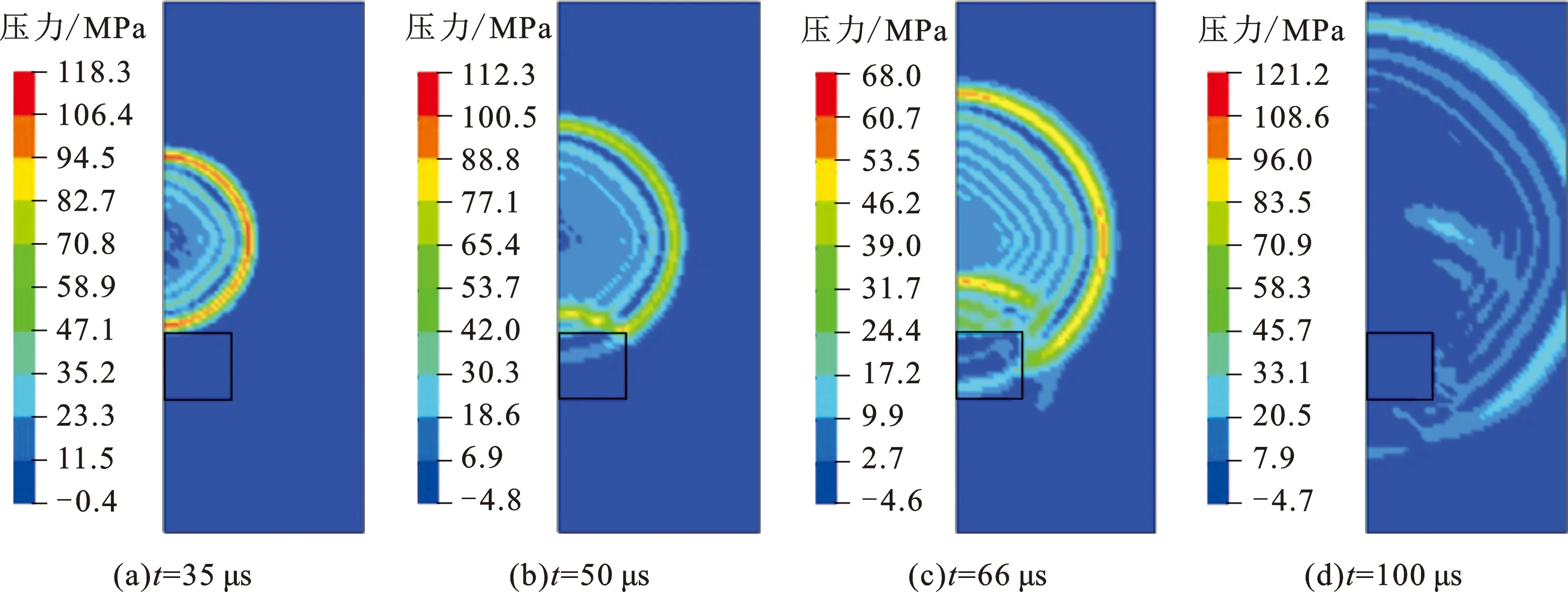
图3 水中冲击波的传播过程
2.2 岩石的破坏过程
不同于水下接触爆炸,炸药起爆后岩石不仅要受到高强度激波的作用,还受到随后产生的爆生气体的作用。使岩石径向上受压,当强度达到岩石的动态损伤阈值时岩石就会产生压剪损伤,而距岩石一定距离处炸药爆炸产生的冲击波对岩石的破坏效果主要是考虑岩石与水的界面处产生的反射拉伸波[9],因为岩石抗压不抗拉,岩石的抗压强度往往是其抗拉强度数10倍,岩石更容易受到拉伸破坏。图4为无围压条件下两组视角下岩石受水下爆炸冲击波的破坏过程。需要说明的是,为了能够清晰看到岩石内部的裂缝分布与冲击波作用下的破坏效果,图4中只显示岩石达到失效条件而删除的单元,隐藏了岩石实际存在的单元。
从图4中可以看出,当t=70 μs时,裂纹主要分布于岩石上表面角部区域A(岩石面H、面h以及面v的交界处),岩石下表面角部区域B(对称面、面H与面h、底面的交界处),岩石侧面边缘区域C(面H、面h的交界附近)。当水中冲击波作用于岩石后,透射进入岩石的冲击波到达面H和面h发生反射,由于水的声阻抗远小于岩石的,所以会向岩石内部反射拉伸波,当由面H反射的拉伸波与面h反射的拉伸波叠加在一起时,在局部产生较大的拉应力,对岩石产生拉伸破坏,区域A与C的裂纹由此产生。区域C的裂纹呈纵向(Y方向)分布,区域A的裂纹围绕着岩石上表面角部区域分布。区域B主要是由于剪切破坏而产生沿X方向的初始裂纹并向内部扩展。当t=80 μs时,冲击波传播到岩石底部并在底面反射,反射波向上传播与爆炸冲击波叠加,在叠加波的作用下,区域C产生不断扩展的横向(平行于XOZ平面)裂纹并且与纵向上的裂纹相互连通,区域B的裂纹也不断向岩石内部增长。当t=90~100 μs时,岩石内部的拉伸波与冲击波叠加作用更为明显,波的传播方向更为复杂,岩石内部裂纹面不断扩大。而且裂纹出现以后会形成新的自由表面,入射波会在自由表面处继续反射拉伸波,当拉伸波足够大或满足一定条件后就会产生二次或多次裂纹。整体上看,岩石裂纹扩展先从岩石角部、岩石面边缘等自由边界处产生,然后逐渐向岩石内部扩展,这种由压力波在自由表面反射所造成的表面动态断裂的过程被称之为“层裂现象”[22]。
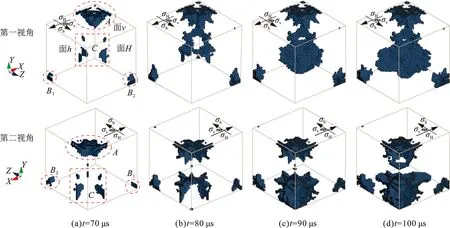
图4 无围压条件下岩石受水下爆炸冲击波下的破坏过程
2.3 围压对裂纹扩展的影响
为了探究围压对岩石的影响,在水下爆破载荷作用于岩石之前对岩石施加σH、σh、σv3向应力。通过控制变量的方法依次探究σv、σH、σh(σH>σh)对裂纹扩展的影响,总共得到40组模拟结果,为了便于观察,取其中12组结果进行分析,具体结果如图5、6、7所示。
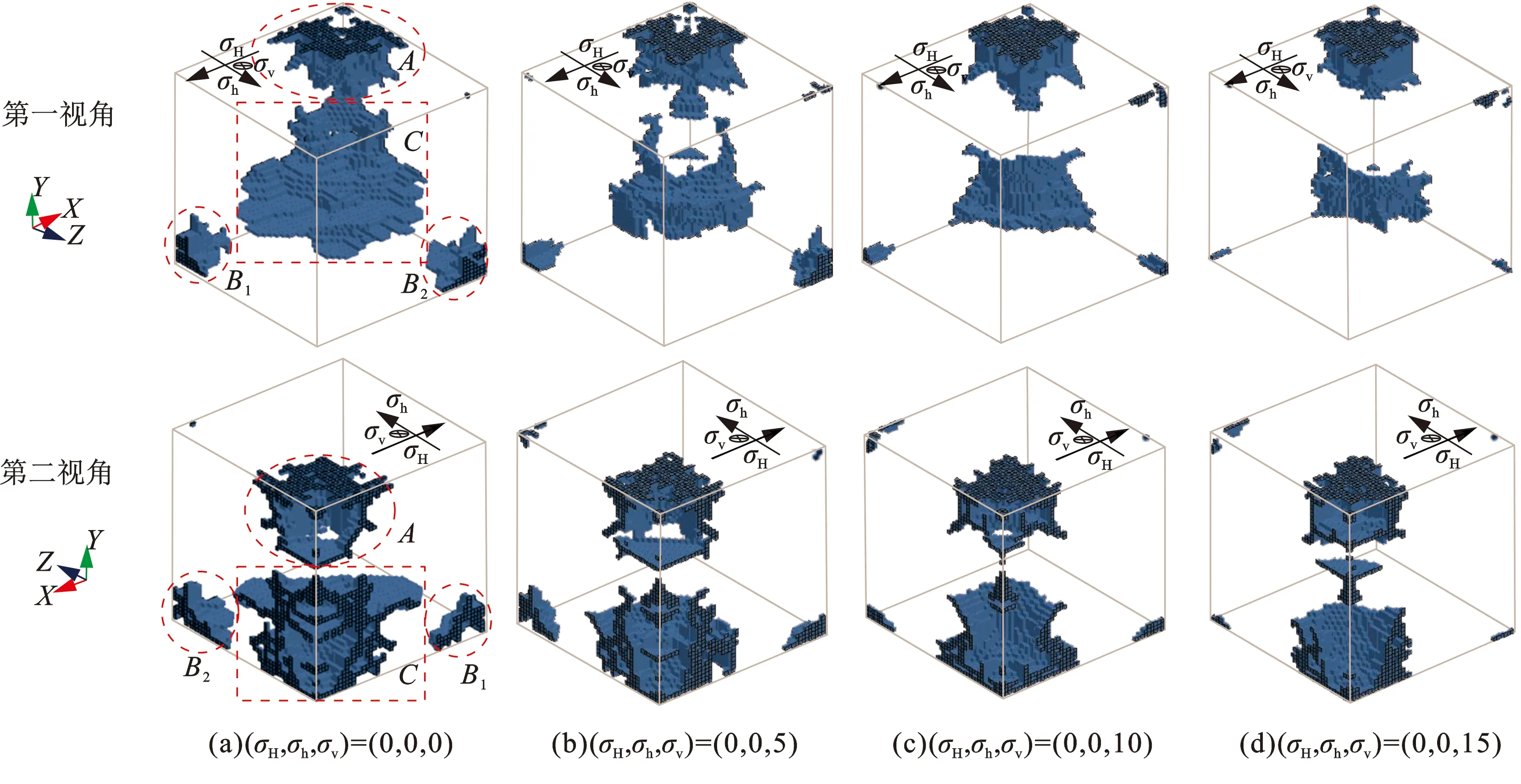
图5 σv变化情况下模拟得到的裂纹分布
从图5可知,爆生裂纹的扩展规模完全受控于围压,随着σv的增大,A、B、C区域的裂纹扩展范围都有不同程度的减小。其中C区域的裂纹扩展缩小最为明显,而且从C区域的裂纹分布可以看到,垂直于应力σv平面内的裂纹扩展长度随σv的增大而减小,向Y方向扩展长度变化不明显。分析其原因,裂纹主要是由拉伸应力引起的,岩石的断裂形式属于张开型,在σv增大的条件下垂直于裂缝面的压应力增加,抑制了平行于平面XOZ裂纹的萌生与扩展。
从图6可以看到:随着σH的增大,A、B、C区域内垂直于应力σH平面内的裂纹逐渐减少;C区域内平行于XOZ面的裂纹逐渐向岩石底面偏移,并且沿着应力σH方向扩展,最终与B1区域裂纹相连通;A区域与B区域内分别沿Y轴负方向与沿Y轴正方向扩展的裂纹逐渐减少,两区域内的裂纹呈平行于XOZ平面间断分布,连接平面之间的裂纹逐渐减少。由于对称性,在只改变σh的情况下也可以看到类似的规律,如图7所示。随着σh的增大,沿Y方向上平行于XOZ面的裂纹增加,并呈片状间断分布于岩石棱边上;A、B、C区域内垂直于应力σh平面内的裂纹逐渐减少;裂纹沿着应力σh方向扩展,最终与B2区域裂纹相连通,岩石底面附近的裂纹扩展范围更广;而且当σh加载到10~15 MPa时,在两对称面交界处的棱边上出现平行于XOZ面扩展的裂纹,并逐渐扩大。分析上述裂纹扩展变化的原因,主要是在σh和σH增大的条件下,垂直于应力σh、σH的裂缝面的压应力增加,不利于裂纹在平行XOY平面内与平行于YOZ平面内的扩展,而且σh和σH增大使平行于应力σv方向平面内的拉应力增大,岩石底面附近的拉应力增加更为明显,使平行于XOZ平面内的裂纹扩展范围更大,甚至产生新的裂纹。
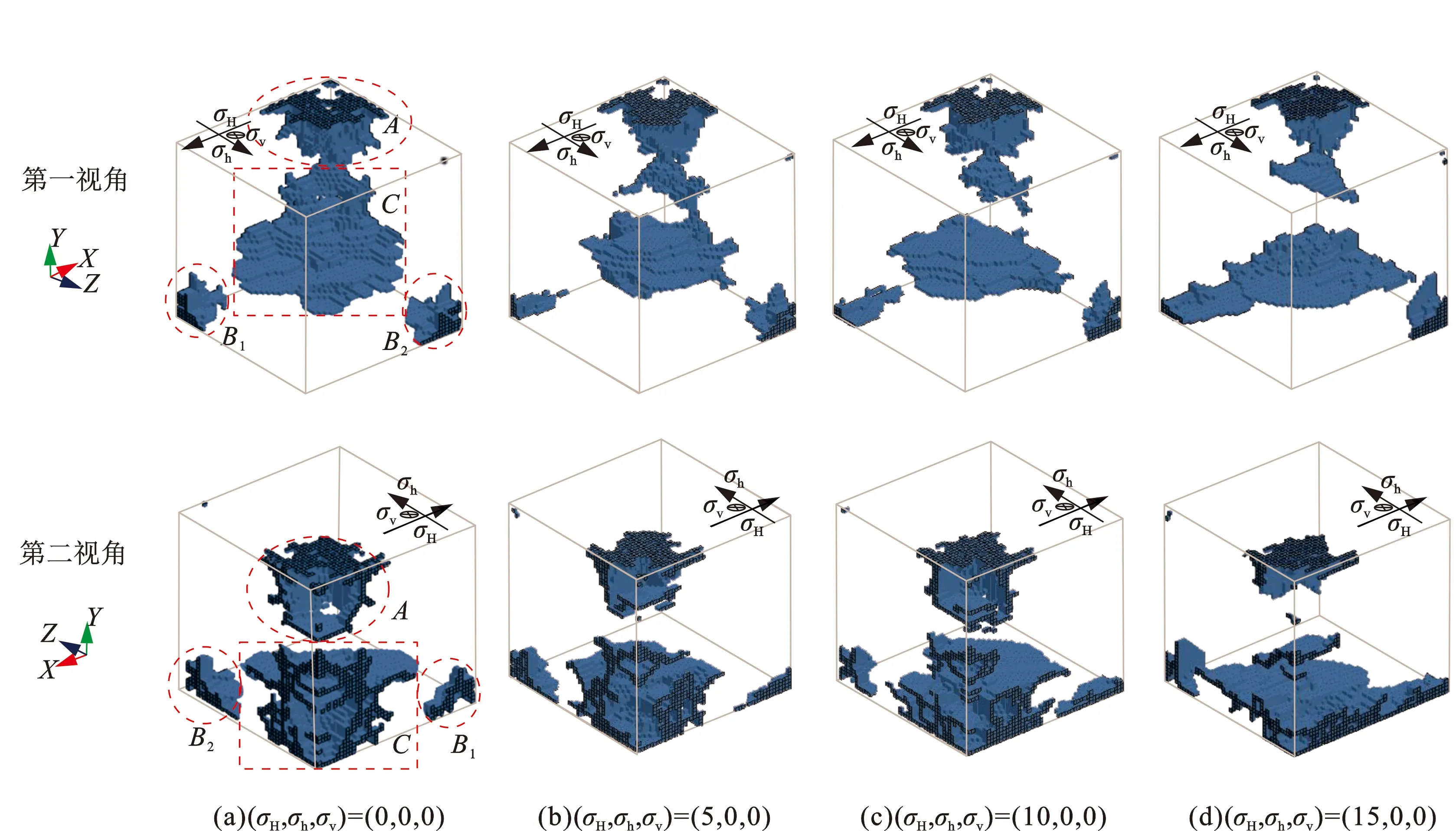
图6 σH变化情况下模拟得到的裂纹分布

图7 σh变化情况下模拟得到的裂纹分布
为了能够定量描述裂纹的影响区域以及水下爆破荷载对岩石的破坏损伤效果,采用Grady和Kipp的理论观点[23],裂纹密度是裂纹影响区岩石的体积与岩石总体积之比,即裂纹密度D为
(7)
式中,V0为岩石总体积,m3;Va为裂纹影响区岩石体积,m3。
依据式(7)对裂纹密度的定义,对构成裂纹单元数目进行统计,裂纹密度可表示为
(8)
式中,N0为岩石总单元数;Na为岩石因满足失效条件而删除的单元数。
对计算结果进行统计、整理并绘制图像,结果如图8所示。由图8(a)可知,在σH=σh的条件下,随着σv的增大,岩石的裂纹密度均会减小,但是并不是σH和σh越大,裂纹密度越大。σH=σh=15 MPa条件下产生的裂纹密度比σH=σh=10 MPa的大,主要原因是σH和σh增大虽然会抑制垂直于两者平面内的裂纹发展,但是会促进平行于两者平面的裂纹增长,尤其是会促进靠近岩石底面附近的裂纹增长,这个现象从图7中也可以看到。这种“抑制作用”与“促进作用”构成了一种竞争关系,在σH=σh<10 MPa时,岩石裂纹扩展主要受到抑制作用,岩石裂纹密度随着σH和σh的同步增大而逐渐减小,而在σH=σh>10 MPa时,主要受到促进作用,裂纹密度增大。在图8(b)中,对同一σH,随着σv增大,裂纹密度呈现不同程度减小;随着σH的增大,除了σv=15 MPa、σh=0 MPa条件下的裂纹密度先增大后减小,其他条件下都呈减小趋势,而在图8(c)中,这种趋势则相反:随着σh增大,裂纹密度呈先减小后增大的趋势。这种随着水平围压的增加,裂纹密度不减反增的结果与以往围压对爆炸产生裂纹的演化规律迥然不同,以往围压载荷降低了裂纹尖端的应力集中程度,初始应力场阻碍了裂纹扩展[24-25],而造成裂纹密度随围压的增大不减反增变化趋势的主要原因还是“抑制作用”与“促进作用”竞争的结果,而这两种相反作用主要源于水下爆炸载荷的作用形式、作用方向与作用大小的特殊性,这与地面钻孔爆破有显著区别。
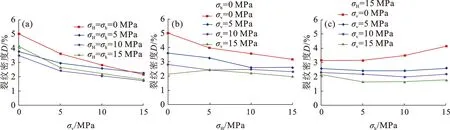
图8 不同围压条件下的裂纹密度
3 结 论
(1)数值模拟得到的水下爆炸冲击波的分布和衰减规律与经验公式结果十分吻合,具有较高的可信度。
(2)岩石在非近距离水下爆破荷载的作用下主要发生拉伸破坏和剪切破坏,裂纹主要分布于岩石上、下表面角部区域,岩石侧面边缘区域,并且裂纹先是从自由边界处产生,然后逐渐向岩石内部扩展。
(3)初始3向应力会抑制与其方向垂直平面内的裂纹扩展;随着与爆破荷载同向的初始应力σv增大,裂纹扩展范围有不同程度的缩小;随着水平初始应力σh和σH增大,使水平面内的初始拉应力增加,角部区域裂纹与岩石侧面边缘区域裂纹相连通,水平面内的裂纹(尤其是岩石底面附近的裂纹)扩展范围更大,甚至在岩石内部产生新裂纹。
(4)采用裂纹密度来较为粗略地表征裂纹的波及范围,不同于陆地钻孔爆破,裂纹的波及范围可能会随着围压的增加而增加,这种特殊性主要由水下爆炸荷载的作用方向、大小和作用形式决定。

