基于可视化技术的电力系统多源协同优化调度研究

陈飞

(云南电力调度控制中心， 云南， 昆明 650011)

0 引言

近年来，由于不可再生能源的日益枯竭，国家大力推行风能、太阳能等可再生能源[1]。这些大容量的可再生能源并网造成电网的稳定性、兼容性及安全性受到较大影响，因此在电网中新能源的消纳问题变得尤为重要[2]。由于可再生能源大多属于不确定能源，产生的电量根据环境实时变化，在并网时会影响到电力系统电网的稳定性，甚至造成电网崩溃，发生大面积停电事故，需要通过火电、水电等可以快速调控的能源来协同调度[3]。

将智能电网可视化技术与能源调度优化算法相结合，在电力系统多源协同调度中，可对电力生产进行动态实时监控[4]。电力系统全网运行过程中的状态和属性可以通过独特的技术和计算方法进行有效处理，把这些状态和属性通过图表、图像等形式表达出来[5]。有助于电力系统操作人员及时掌握电力系统的综合情况，使得参数在配置上更加合理和科学，从而提高电力资源配置的工作效率[6]。

本文在等高线模型的基础上，构建了含有大规模风电、光伏太阳能等新能源协同优化的多目标模型[7]。采用将多目标遗传算法和粒子群优化算法相结合的协同优化(HCOS)调度计算方法。在确保电力系统安全稳定运行的前提下，通过合理的调峰、调频、储能工作来调整能源匹配，实现风光火储发电的经济性[8]。有效克服了风能、太阳能等不确定性，能源的随机性、波动性和间歇性等给电网带来的不利影响[9]。

1 基于可视化技术的电力系统多源协同优化调度

1.1 电力系统等值线可视化

随着科学技术的不断发展和进步，在电力系统实时监控中，电力系统实时运行数据更多的是潮流图上实时显示的[10]。显示在潮流图上的动态实时数据虽然非常准确，但对于整个电网而言，要实时监控全网所有信息，并要对信息做出相应的反应[11]。仅仅依靠显示数字不但繁琐复杂而且单调，缺乏直观性和全局性，数据间的相互关系也不明确[12]。急需一些方法和工具能够全面、快速、直观监控电网运行状况。可视化技术的出现为这些需求提供了解决方法，该方法反映数据更具体、直观且可以用于配电数据的预测，因而受到研究人员的重视[13]。

本文采用等值高线法构建电力系统模型，利用地图上任一点P(x，y)的负荷作为该点的高度值h，根据坐标(x,y,h)构建三维空间的曲面模型[14]。进一步根据地形学，将高度信息投射到平面上生成等高线信息，从而形成区域用电模型图[15]。电网等高线图生成步骤如图1所示。

图1 电力系统等高线模型生成步骤

1.1.1 三角形网格化处理

对于等高线的网格构建来说，其主要的方法包括网格序列法和网格无关法。序列法构建效率低，因此本文选用利用拓扑关系插值生成的三角形网格无关法[16]。

基于局部优化算法对Delaunay三角网图形进行优化，使得最终生成的网格计算效率更高。该网格的生成结果如图2所示，具体步骤如下。

图2 三角形网格生成结果

(1) 将离散数据点坐标数据进行排序，按照坐标位置进行从小到大，从x到y的位置重布。

(2) 连接前2个数据点，生成线段AB。

(3) 取其后紧挨的2个数据点中距离更近的点为C点，构建三角形ABC。

(4) 构建结构体，并依次取剩余点中的前两点D、E。并判断其距AB、BC、CA三条边中点的距离大小，如D点距BC距离是所有上述距离中最小值，连接DB、DC构成新三角形。

(5) 运用LOP方法对构建的三角形进行优化，保证最小内角最大化原则。

(6) 重复构建结构体，直到所有节点都被连接，算法完成。

1.1.2 网格加密处理

为了提高模型的精度，使等高线的排布更细致，可以通过增加离散点的方法，对已经构建好的三角形进行网格加密处理。

增加的离散点主要包括三角形的中点、重心以及任意随机点等。但是为了保证构建后的三角形结构更平衡，效果更稳定，本文选用重心插值的方法，加密后的三角形如图3所示。

图3 重心插值法构建的新三角形

1.1.3 等值线处理方法

将所得到的三角形网格根据其点坐标的高度值h，将其投影到水平平面上，从而可以得到相应的等值线图。为了使等值线更细致，图形反映更清楚，需要将高度值h按等级划分，从而可以得到依次递进的分布图，由绘图区可知，闭合的等值线一定位于图区内部，且区域相连，开放的等值线一定位于边界。

等值线处理的过程采用一定的规则将等值线的线段转换成表格，进而用于计算机的计算分析，整个处理的过程如下(如图4)。

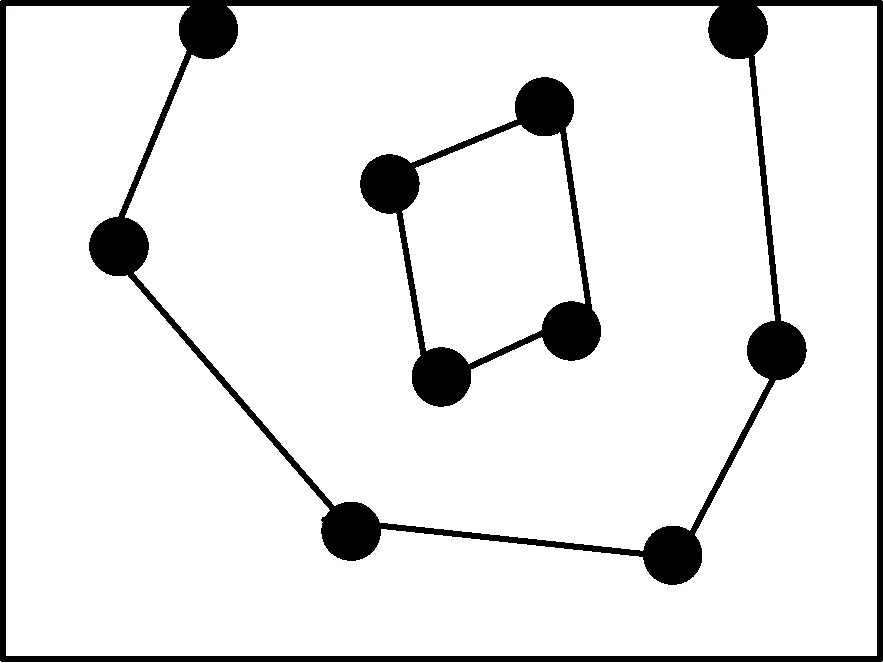
图4 等值线追踪示意图

(1) 按照图形规则，在绘图区的边界处寻找数据端点。比较边界三角形的h值，比较得到最小值作为等值线端点。

(2) 在端点位置的周围进行比较，寻找等值点，两点数值相等时，用线段连接，不等时寻找下一点，已连过的点在数据库中抹去，避免重复查找。

(3) 直到数据点周围的标记点全部被查找后，未发现等值点，则最低电压等级搜索结束。

(4) 选择低一等级的等值点，重复上述操作，直至所有数据全部被查找完毕。构建好的等值线图如图5所示。

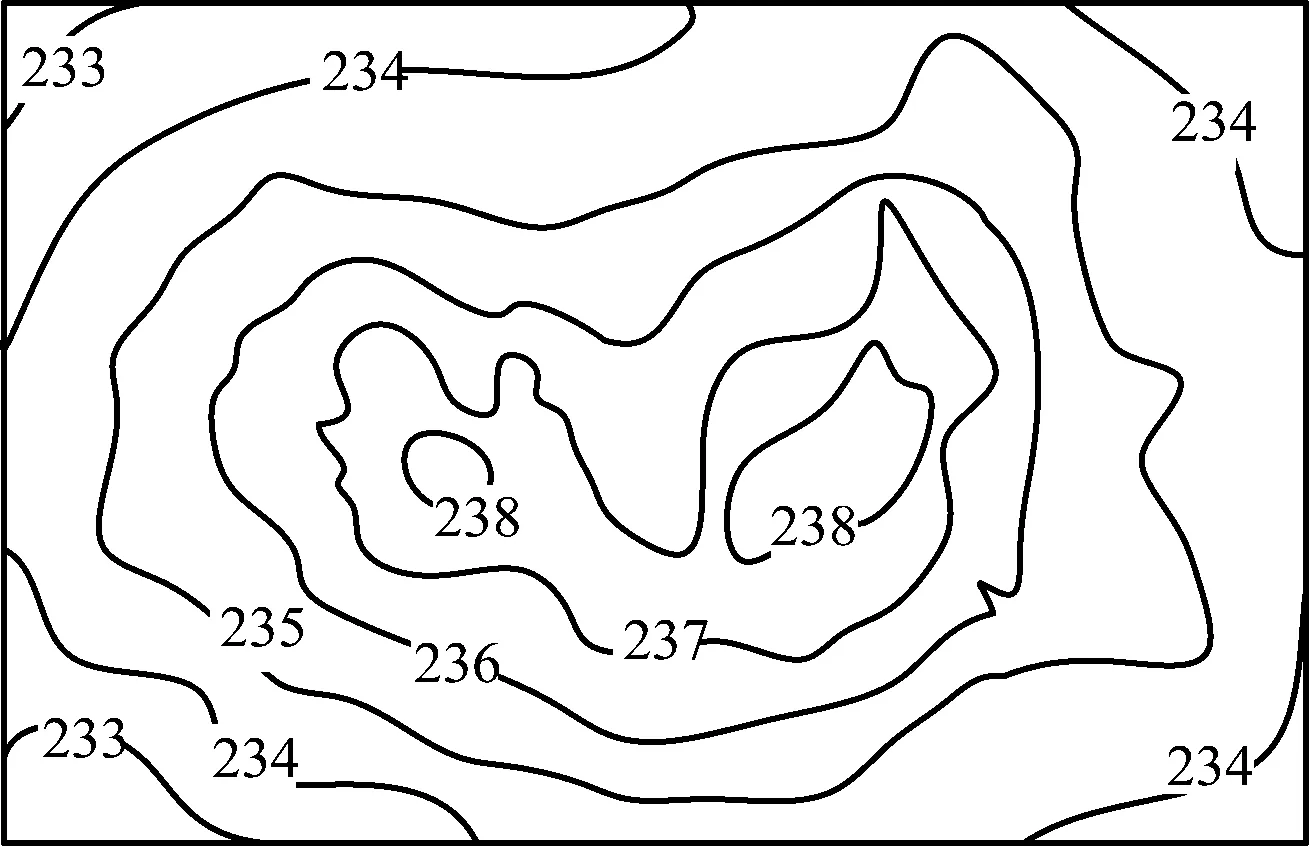
图5 生成后的等值线分布图

1.2 多源协同优化调度的设计与实现

1.2.1 设计的总体思路与原则

在可视化监控的基础上，根据构建的等值线模型，构建光能、风能等不确定能源的输出情况，并与整体的消耗情况进行对比，最大限度的利用可再生能源进行电力供给。不足和波动的部分采用储能、火电等能源进行补充，实时监控系统的运行情况，整个系统的工作原理图如图6所示。

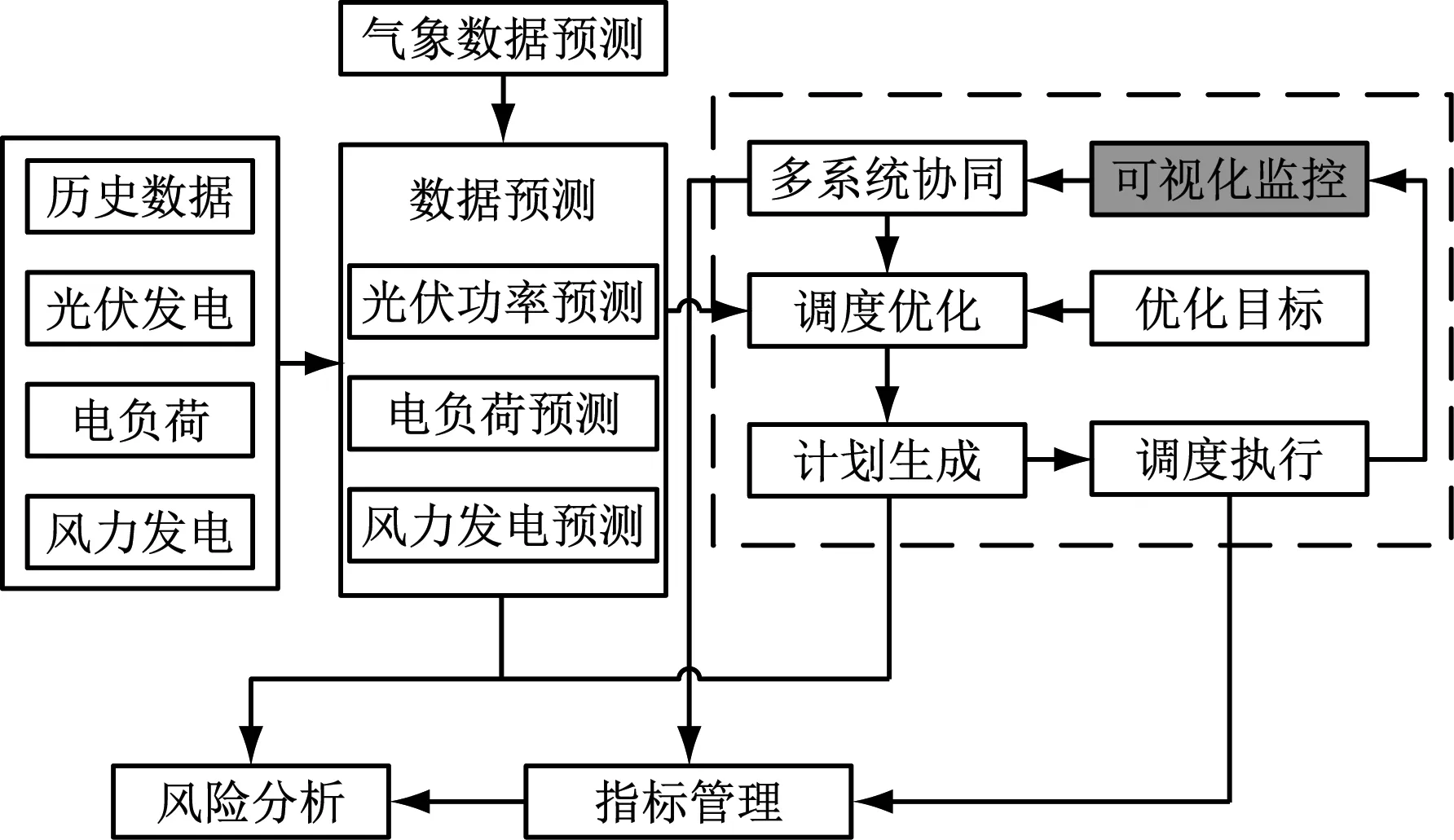
图6 电力系统多源协同优化调度

1.2.2 风光储火多源互补系统调度模型

本着系统稳定性最高，效率最高的原则，对整个系统的目标进行设定。设定目标为需要补充的差值负荷最稳定，峰值最低，构建目标函数。公式为

Pb(t)=Pc(t)-Pw(t)-Ps(t)-Pd(t)

(1)

其中，Pb(t)为备用差值负荷，Pc(t)为常规能源消耗，Pw(t)为模型预测风能，Ps(t)为模型预测的太阳能，Pd(t)为电池功率。

差值负荷的平均功率为

(2)

目标函数表示为

(3)

为了保证差值负荷的峰值最低，需要使整个周期内，有

minF2=min(max(Pb(t))T)

(4)

1.2.3 HCOS算法

对于电力系统的调度来说，需要构建的函数主要包括风能、太阳能、消耗、储备能和应急火电能源等多个部分，如果采用传统的粒子群算法的话，会面临多维多目标优化，空间大、求解难，数据繁复的困难。为了解决这个问题，本文提出了HCOS算法。

HCOS算法采用分层分级的方式，对整个系统进行优化，主要分两个层级。第一层利用多目标的遗传算法，在等值线模型的基础上，对风能、太阳能、电池储能和消耗总体能源进行预测，保证两个目标的协调。第二层利用粒子群算法对火电机组进行优化，保证整个系统的能源消耗和工作成本最低。利用随机粒子群，构建二进制变量，使得粒子只具备开和关两种状态，将其分配给火电机组，添加火电机组的开关机最短时间等约束条件，按照机组运行成本效率从高到低的顺序，依次开启火电机组，直至满足差值负荷的需求为止。根据剩余能耗的情况进行系统优化，保证整个满足条件的火电系统的效率最高，成本最低。

通过两级优化，避免了粒子群算法工作量大的问题，同时保证了系统的成本、效率最优，相比于粒子群算法，HCOS算法的变量更少，约束条件也少，因而优化时间更快，效率更高。其算法流程图如图7所示。

图7 HCOS算法流程图

2 实验分析和讨论

以华东某区为例，通过等值线的方式，构建该区域的用电耗电统计数据。从而实时预测其负荷分布，用于电力系统配电调控。整个区的全部面积约为1 200平方公里，用户总量超过200万户，2014年共计消耗电能约250亿度，实时峰值功率约650万千瓦。整个区域内部大型设施齐全，符合现代化都市的特征。

由图8可知，基于可视化技术，采用等值线法可以对该区域的用电负荷情况进行预测，并将预测结果与传统的ESM方法进行比较，从结果上可以看出，传统方法的预测误差约为6%左右，而本文的方法，预测误差约为4%，说明本文采用的方法对于电力的评估预测具有比较好的效果。由图8(b)可知在相同的置信度下，传统方法的预测精度约为80%，而本文采用的方法，其预测精度可以达到90%，证明该方法的优越性，可以更有效的对电力系统的负荷情况做出准确的预估。

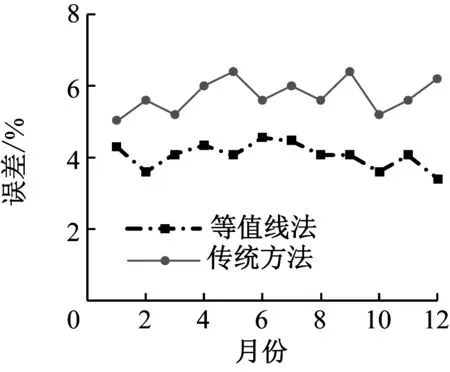
(a) 预测误差分布

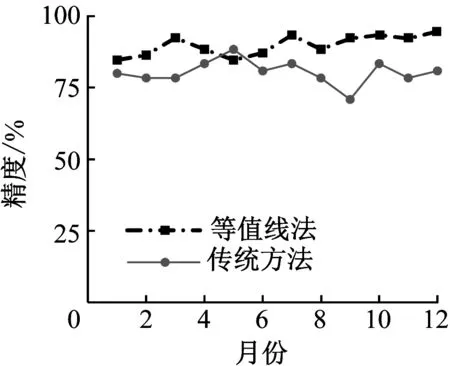
(b) 97%置信度下的预测精度图8 等值线法用电负荷预测结果

在模型精确的基础上，本文采用HCOS方法对于电力系统进行多源协同的资源优化调度。仿真条件设定这个电力系统的资源包括风电电场、太阳能电站、电池储能电站各一个，火电厂待工作机组10个，从而构成一个风光储火的多源电力系统。利用传统的粒子群算法和本文提出HCOS算法分别对该系统进行资源协调，以小时为单位，设定仿真周期为24 h，电池储能电站的容量设定为350 MW，充放电效率为0.95，并假定整个系统的漏电率为1.5%，计算其火电机组的运行成本为

(5)

其中，Prl为供给容量，Ey为有效发电量，Tz为投资折旧成本，Ts为燃烧成本。从而对火电机组的运行状态进行监控，在不同装机供给容量下，核算不同算法的运行成本如表1所示。

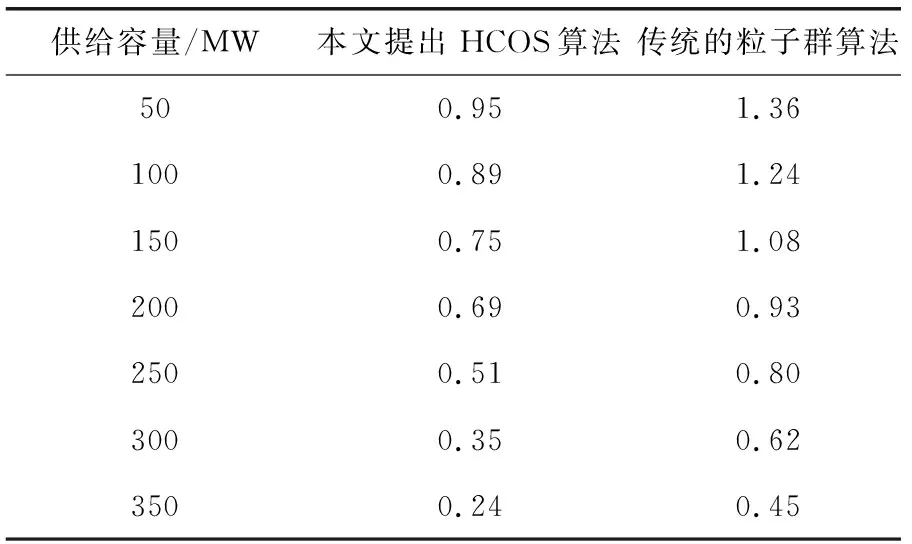
表1 两种算法运行成本对比结果

根据表1中的数据可知，随着供给容量的增大，两种算法的运行成本随之降低，当供给容量为50 MW时，本文提出HCOS算法的运行成本最大为0.95，而传统的粒子群算法的运行成本最大为1.36；当供给容量为350 MW时，本文提出HCOS算法的运行成本最小为0.24，而传统的粒子群算法的运行成本最小为0.45。由此可知，相比传统的粒子群算法，本文提出HCOS算法的运行成本较小，因为本文提出HCOS算法采用分层分级方式，利用粒子群算法，优化火电机组，保证整个系统的能源消耗和工作成本最低，从而节约了整体发电成本，提高了电力系统的经济性。

采用分层求解的方式，先利用多目标遗传算法求得这个系统中的最优解，然后将得到的解代入到粒子群算法中，求得火力电站供电机组的出力部分，保证得到的解复合算法的目标设定条件。将求得的解记录在数据系统中，得到如图9所示的功率分配情况。

图9 HCOS算法计算出的最优机组功率分配

计算结果如图10所示，从图10中整个周期可以看出，相对于传统的粒子群算法，HCOS算法的计算结果系统更稳定，差值负荷的波动更小，从而可以使得火电机组工作更稳定，需要启停的次数更少，证明该算法的优越性。

同时，对于白天由于光伏电站系统的工作，向整个电网输出电能，使得需要迅速协调火电机组情况，图10中可以看出，在早六点至晚六点的光伏电站工作时间，本算法的预测精度更高，快速有效的调整系统火电输出，有效避免了应急措施不急情况下的大范围输出波动，造成能源的浪费。对于风电等具有实时变化特性的能源供应，该算法反映更灵敏，预估更准确，波动更小。而且该算法求解内容更少，速度更快，综合各方面优于传统算法，为电力系统多源互补优化调度提供了一种有效优化途径。

为了进一步验证优化后电力系统的安全性，设定该电力系统的用电负荷稳定范围为800～1 200 kW·h，超出该范围电力系统会出现运行异常情况。利用传统的粒子群算法和本文提出HCOS算法分别对该系统进行资源协调，得到两种算法用电负荷波动情况如图11所示。

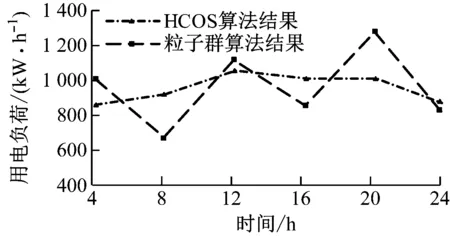
图11 两种算法用电负荷波动情况

根据图11可知，当时间运行至24 h时，本文提出HCOS算法的用电负荷始终在800～1 200 kW·h的范围内，而传统的粒子群算法的用电负荷超出了800～1 200 kW·h的范围。由此可知，本文提出HCOS算法优化后电力系统的安全性较高。因为当电力系统出现电源发电负荷大范围波动，运行异常，突发紧急情况时，本文提出HCOS算法优化后的监控系统可以立刻发出响应，进入到紧急报警处理模式，启动紧急预案。根据能源需求侧的响应，协同调度各能源，从而平抑系统潜在的运行风险。电力系统需要协调能源发电、储能系统、能源用户三者关系，在确保最经济运行的条件下，使三者关系达到最佳。

3 结束语

本文通过对可视化技术下的电力系统多源协同优化调度相关内容的研究。针对目前大规模的风电，光伏太阳能等新能源并网而导致电网运行不稳定问题，通过构建等值线模型，提出了一种解决多目标和多约束问题的HCOS优化算法。

目标设定原则采用风光等可再生能源贡献最大，火电补充波动最小，成本最低为基本原则。在这个基础上通过分层计算构建了HCOS算法，实验结果证明该算法多方面都优于传统的粒子群算法。

基于可视化技术，对全网电力系统做出精确监控和预测，使得供电系统可以有效保证工作效率。结合数据优化和人工智能，迅速有效的保证电网系统工作运行稳定，具有较好的应用价值，为电力系统的进一步发展提供了新的思路。