基于大数据分析技术的运动员成绩建模与估计研究

李严， 杨改红

(西安交通大学城市学院， 体育部， 陕西， 西安 710018)

0 引言

精准估计运动员成绩，可为其制定更加完善的训练规划，确保运动员在比赛中获取更好的成绩[1]，因此估计运动员成绩显得格外重要。最初的运动员成绩估计方法为教练通过统计学方法对运动员成绩实施计算与估计，但教练不可能考虑到影响运动员成绩的全部因素，且计算过程较为繁琐，运动员成绩估计效率低，不能满足现代运动员训练的要求[2]。

文献[3]提出最小二乘支持向量机和预测误差校正的运动员成绩预测模型。首先通过提升小波和最小二乘支持向量机对运动员成绩进行建模和预测;然后通过误差校正方式对运动员成绩的预测结果进行校正;最后通过运动员成绩预测实例对模型的有效性进行测试。结果表明，所提模型通过误差校正提高了运动员成绩预测结果的稳定性。文献[4]提出基于混沌理论和机器学习算法的运动员成绩预测模型。对运动员成绩数据进行分析，根据混沌理论提取运动员成绩的变化特点，利用神经网络构建成绩样本分析模型，通过粒子群算法优化神经网络模型参数。结果表明，该模型可有效提高预测结果的准确度。文献[5]提出了一种复杂的以无针对性的模型，分析了田径短跑运动员的不同测试和变量，结合了数学和计算模型来分析跑步锻炼条件下的人体测量学、生物力学和生理学相互作用。通过复杂的网络和数学输出相关的运动测试确定在跑步过程中的重要因素。上述方法仅从运动员外部影响的角度对其成绩进行预测，并且预测结果仅体现了整体变化趋势。

为此，本文提出基于大数据分析技术的运动员成绩建模与估计方法，为运动员可以得到更好的发展提供数据支持。

1 运动员成绩建模与估计

1.1 支持向量回归机估计模型

1.1.1 损失函数

利用大数据分析技术可以预测未来，通过数据角度分析特征间的关系获取更深层次的数据分析方法[6]。该技术主要利用机器学习技术实施归纳推理数据，在运动员成绩相关数据内获取潜在的模式，实现运动员成绩估计。在机器学习技术中，计算过程较为简便的是支持向量回归机算法[7]。为实现支持向量回归机计算的最优化，首先计算最小化损失函数，计算方法如式(1)：

(1)

式中，预期设定的输出结果为a，真实的输出结果为b。为获取回归函数y的最优估计值，降低估计值计算中的误差，采用经验风险最小化原则进行计算。由于在出现异常点时，会对最小二乘估计器的运算产生较大影响，因此需要一种鲁棒性较强的估计器。估计器设计目标是鲁棒性，针对全部鲁棒性的数值度量一定要考虑受微小噪声模型的一个偏差ε形成的最大性能退化。因此，回归计算过程中，将绝对误差当作被最小化的值，即损失函数的具体形式如式(2)：

L(a,b)=|a-b|

(2)

1.1.2 支持向量回归机

输入空间内已定的运动员历史成绩训练集是T={(x1,y1),(x2,y2),…,(xl,yl)}⊂Rd×R，其中xi为第i个运动员历史成绩学习样本的输入值，yi∈R属于相应的目标值。在高位特征空间内，组建最优线性函数公式如式(3)：

f(X)=WTφ(X)+|a-b|

(3)

式中，权重为W,偏置项为b,线性函数为φ(X)。

依据式(2)损失函数的扩展建立实值函数支持向量回归机，如式(4)：

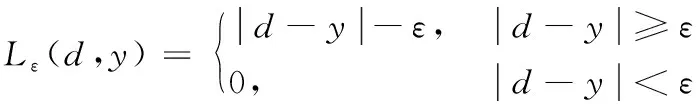
(4)

式中，指定参数为ε,损失函数Lε(d,y)也叫ε-不敏感损失函数。

(5)

式中，不敏感损失函数参数ε>0，正则化参数C属于控制超过误差范围的学习样本的惩罚程度。

由于支持向量回归机无法对原始问题进行求解计算，因此通过计算支持向量回归机的对偶问题以获取模型参数的最优解[10]。采用Lagrange乘子方法，依据核函数方法获取支持向量回归机的Wolfe对偶规划形式：

(6)

由求解支持向量回归机的对偶问题获取原始问题的解，建立决策函数。如果目标函数式(6)中的内积φ(xi)·φ(xj)由K(x,x′)替换，那么可获取ε-支持向量回归机算法。获取式(6)的最优解α(*)后，仅有少数参数(α*-α)不等于零，与其相应的xj就是问题范围内的支持向量[11]。由学习获取回归估计函数：

(7)

式中，N为运动员成绩训练集数量。

1.2 粒子群算法原理

利用粒子群优化算法优化支持向量回归机训练时的各个参数，获取最优参数[12]，利用最优参数提升运动员成绩建模与估计的准确性。粒子群优化算法内的各个优化问题的解均属于搜索空间内的一只鸟即粒子[13]，在搜索空间内按照一定的速度飞行，通过自身的飞行经验与同伴的飞行经验动态更改飞行速度[14]，各个粒子的坐标是Qm=(qm1,qm2,…,qmD)，各个粒子的飞行速度是Vm=(vm1,vm2,…,vmD)，各个粒子均存在一个通过优化目标函数获取的适应值[15]，针对第m个粒子，该粒子经过的历史最好位置是Pm=(pm1,pm2,…,pmD)，即个体极值pbest；整个群体内全部粒子获取的最好位置是Pg=(g1,g2,…,gD)，即全局极值gbest。粒子是通过个体极值与全局极值持续调整自身的速度与位置，迭代k次粒子的飞行速度与位置：

(8)

式中，在区间[0,1]内的随机数是r1与r2，权重因子是z1与z2，惯性权重函数是ω。

1.3 运动员成绩建模与估计

基于大数据分析技术的运动员成绩建模与估计的工作流程如图1所示。

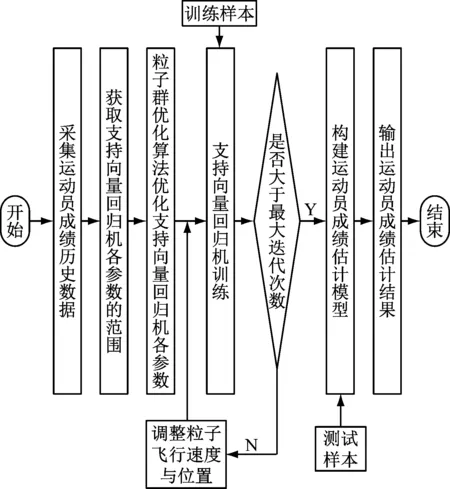
图1 运动员成绩建模与估计工作流程图

大数据分析技术的运动员成绩建模与估计步骤如下。

(1) 采集运动员成绩的历史数据，对运动员的历史数据进行处理获取运动员成绩范围：

(9)

式中，运动员成绩的最大值是xmax，运动员成绩的最小值是xmin。

(2) 利用粒子群优化算法优化支持向量回归机各参数。

(3) 按照各组参数对运动员成绩进行训练，通过支持向量回归机实施学习。

(4) 若迭代次数大于已设置的最大值，则结束算法；若迭代次数小于已设置的最大值，则调整粒子群的飞行速度与位置。

(5) 增加粒子群优化算法的迭代次数。

(6) 通过支持向量回归机的最优参数重新训练运动员成绩，通过最优解pbest与gbest获取支持向量回归机的最优参数。构建基于支持向量回归机的运动员成绩估计模型。

(7) 通过运动员成绩测试样本对运动员成绩估计模型的性能实施测试与分析，输出最终运动员成绩估计结果。

2 仿真实验

2.1 数据来源

以某校运动员为实验对象，该校包含100 m跑、马拉松、田径、游泳、举重与三级跳远等多种类型的运动员。首先以三级跳远为例，对三级跳远运动员成绩实施测试，共包含200名三级跳远运动员成绩。其中前100个数据当作训练样本利用所提方法构建运动员成绩估计模型，其余100个数据当作测试数据，200名三级跳远运动员成绩历史分布如图2所示。

图2 跳远成绩历史分布图

2.2 有效性分析

利用所提方法估计100名三级跳远运动员的成绩，估计结果如图3所示。根据图3可知，所提方法能够有效估计100个三级跳远运动员的跳远成绩，且与实际三级跳远运动员的成绩差距较小。实验证明：所提方法能够精准估计运动员成绩。

图3 估计结果

2.3 准确性与估计效率分析

为测试所提方法的准确性与估计效率，利用所提方法与文献[3]方法、文献[4]方法选取多种类型的运动员实施测试，三种方法对多种类型运动员成绩估计精度如表1所示。根据表1可知，针对不同类型的运动员，所提方法的运动员成绩估计精度明显高于其余两种方法，所提方法可适用于任意类型的运动员成绩估计，可最大程度上降低运动员成绩预测过程中产生的误差，预测结果的可信度较高。

表1 三种方法的估计精度

三种方法的估计时间如表2所示。根据表2可知，针对不同类型的运动员，所提方法的运动员成绩估计时间明显低于其余两种方法，运动员成绩估计效率更高。

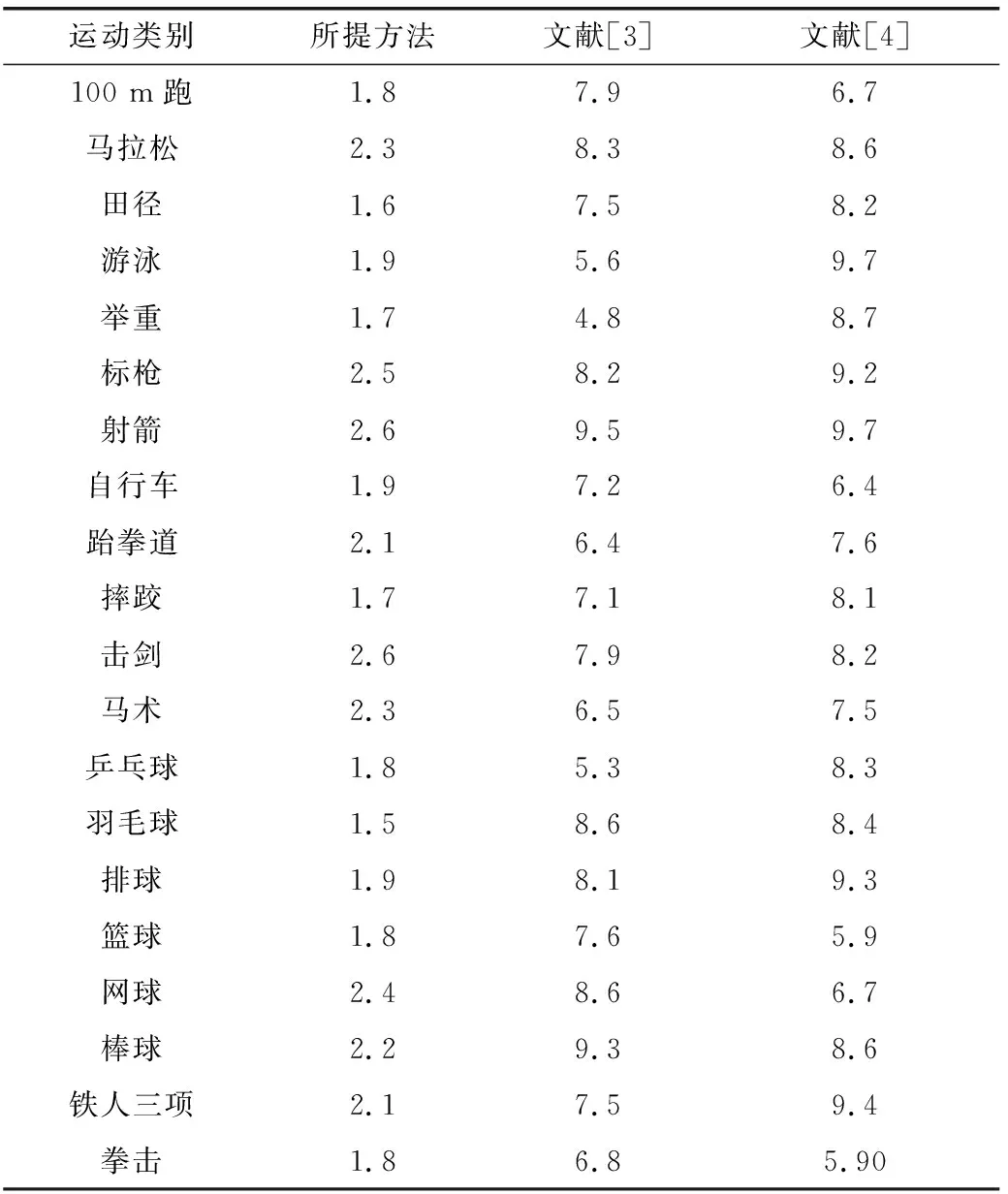
表2 三种方法的估计时间 单位：s

为进一步验证所提方法的准确性，以三级跳远运动员成绩为例，在三级跳远运动员历史数据中加入不同大小高斯噪声，利用三种方法估计100名三级跳远运动员成绩，在不同高斯噪声时，三种方法的误差如图4所示。根据图4可知，随着高斯噪声的不断增加，三种方法的MAE值均随之提升，在不同高斯噪声时，所提方法的MAE值均明显低于其余两种方法，且所提方法的MAE值提升幅度明显低于其余两种方法。实验证明：在不同高斯噪声时，所提方法的MAE值最低表示所提方法的估计值与实际值最为接近，具备更好的估计效果。

图4 三种方法的误差评价指标对比图根

3 总结

运动员训练研究的关键为运动员成绩估计问题，通过估计运动员成绩可为其制定不同程度的训练，进一步提升运动员成绩，使其更加优秀；因此研究基于大数据分析技术的运动员成绩建模与估计方法，从而提升运动员成绩估计精度与估计效率，增强运动员成绩估计结果的可靠性，为运动员训练提供更有价值的信息。