基于人工蜂群算法的海上风机TMD振动控制研究
卢 东 哲, 王 文 华*, 李 昕, 韩 付 成, 李 颖
( 1.大连理工大学 建设工程学部 海岸和近海工程国家重点实验室, 辽宁 大连 116024;2.浙江科技学院 中德工程师学院, 浙江 杭州 310023 )
0 引 言
服役期间,海上风机结构在风、浪作用下易产生振动和变形,常因疲劳、失稳等原因发生破坏[1].而调谐质量阻尼器(TMD)因其简单性和实用性成为国内外学者解决海上风机结构减振问题的研究热点.Lackner等[2]、Ghassempour等[3]基于单桩式海上风机整体耦合模型,通过穷举法试算了多组TMD质量、刚度和阻尼参数,分别以等效疲劳荷载和塔筒顶部位移为评价指标确定最优TMD参数.Stewart等[4-5]建立了两自由度的单桩式海上风机-TMD运动方程,在给定TMD质量参数下基于遗传算法得到最优TMD刚度、阻尼参数,并以疲劳寿命为评价指标验证了优化后的TMD减振效果.贺尔铭等[6]建立浮式风机-TMD的耦合动力模型,利用穷举法得到最优TMD参数并在多种典型工况下对其进行模拟仿真,结果表明经过参数优化后的TMD能够明显抑制驳船式风机叶片和塔筒振动.金鑫等[7]基于海上风机-TMD两质点简化计算模型,以动力放大系数为优化目标利用单纯形遗传算法搜索最优TMD刚度和阻尼参数,探讨了经过参数优化后的TMD对海上风机结构关键部位位移和荷载的影响.
本文建立包含海上风机结构一阶弯曲自由度和TMD水平运动自由度的两自由度简化数值仿真模型,并基于此采用人工蜂群(ABC)算法[8]对TMD的刚度和阻尼参数进行优化设计.进一步,基于空气动力-水动力-结构动力-控制系统整体耦合分析方法,利用FAST v8[9]建立导管架式海上风机-TMD整体耦合计算模型对优化后的TMD在正常和停机工况下的适用性及其减振机理进行研究,为导管架式海上风机结构的被动控制研究提供一定的参考.
1 基于海上风机简化模型的TMD优化理论
1.1 海上风机-TMD两自由度计算理论
基于小变形假定,选取海上风机结构一阶弯曲模态和TMD水平运动作为主自由度,将海上风机-TMD结构简化为两自由度体系,随机激励W(t)作用下海上风机-TMD两自由度体系计算模型如图1所示,可得如式(1)、(2)所示运动方程[10]:

图1 海上风机-TMD两自由度简化计算模型Fig.1 Simplified two degrees of freedom numerical model of OWT-TMD
(1)
(2)

为便于建立结构位移响应方差数学模型,假定随机激励为白噪声随机过程,其频谱密度为S0,利用维纳-辛钦关系,基于传递函数解法[10],便可推导出海上风机结构位移反应x1方差:
(3)
其中
D1=4ζ1(1+μ)f2
B1=4(1+μ)f2
B2=4ζ1f[1+(1+μ)f2]
B4=ζ1μf2
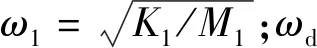
1.2 基于人工蜂群算法的TMD参数优化方法
人工蜂群算法是一种基于蜂群智能行为的优化算法,在解决多变量函数优化问题时,相比于遗传算法、粒子群算法和粒子群进化算法,其优点在于鲁棒性强,在每次迭代过程中都会进行全局和局部的最优解搜索,可避免陷入局部极值[11],且收敛速度快.
人工蜂群算法通常依据雇佣蜂、观察蜂、侦查蜂寻找最佳蜜源,其过程分为4个阶段.
(1)初始阶段
(4)

(2)雇佣蜂阶段
每只雇佣蜂利用其当前解xij计算其蜜源量fi和适应度gi,适应度计算如式(5)所示,并采用式(6)随机搜索新解x′ij.在得到新解后,采用式(5)重新计算其蜜源量f′i和适应度g′i,当新解的适应度g′i大于旧解的适应度gi时,采用新解继续搜索,否则被抛弃.
(5)
x′ij=xij+φij(xij-xkj)+ψij(xbj-xij)
(6)
式中:fi为第i个食物源的蜜源量,即第i个解的目标函数值;k为随机选择索引,k=1,2,…,nf且k≠i;φij为[-1,1]的随机数;ψij为[0,1.5]内的均匀随机数;xbj为第j维全局最优解;x′ij为生成的新解.
(3)观察蜂阶段
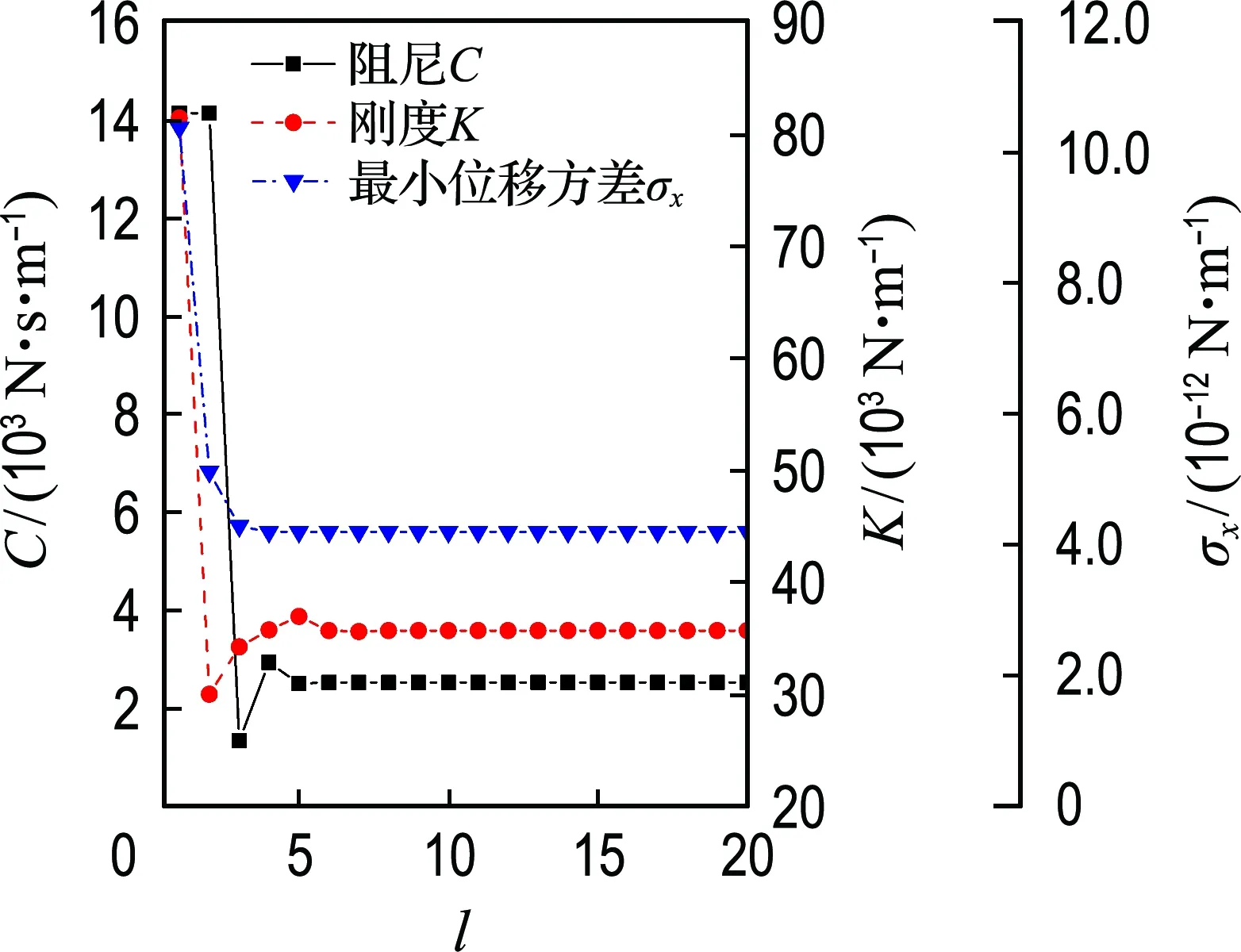
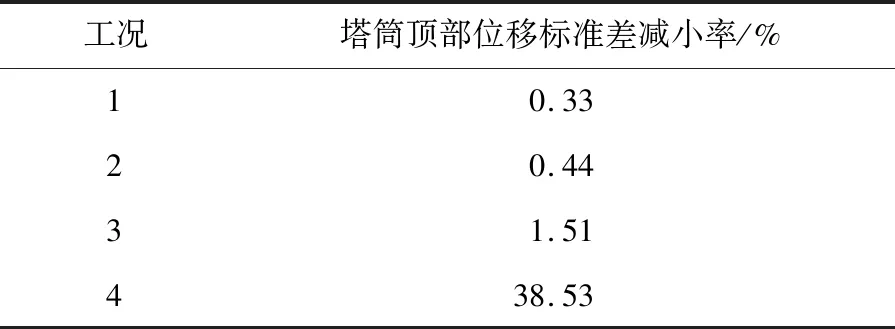
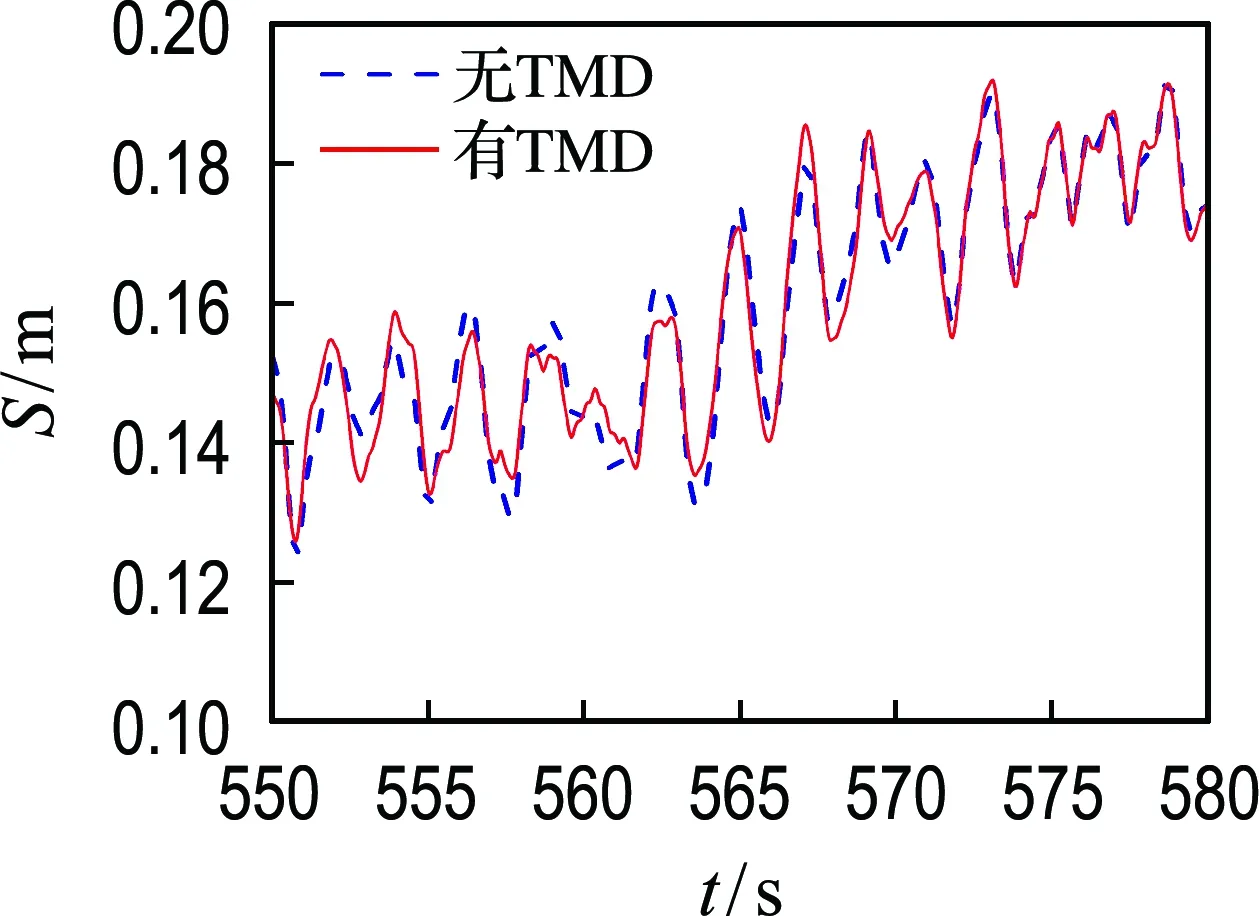
观察蜂依据式(7)计算得到适应度分布概率pi,并在[0,1]产生一个随机值r,当r (7) (4)侦查蜂阶段 (8) 其中lβ为Levy飞行步长. 本研究以白噪声随机过程下海上风机-TMD两自由度简化模型所得结构位移标准差最小为优化目标,采用人工蜂群算法开展适用于海上风机结构一阶弯曲自由度被动调谐减振控制的TMD刚度和阻尼参数优化设计研究,提出的优化设计流程如图2所示. 图2 人工蜂群算法流程图Fig.2 Flow chart of ABC algorithm 本文基于美国可再生能源实验室(NREL)开发的5 MW[12]海上风机模型开展振动控制分析,该模型主要参数如表1所示.根据5 MW海上风机切入和额定转速可确定1 P和3 P允许的频率为0.22~0.32 Hz.海上风机基础结构采用OC4项目导管架基础结构[13],基础顶面长和宽均为9.6 m,基础底面长和宽均为12 m,导管架基础结构参数如图3所示.基础结构杆件的弹性模量E为210 GPa,剪切模量G为80.8 GPa,密度ρ为7 850 kg·m-3. 表1 NREL 5 MW基准风机主要参数Tab.1 Main parameters of NREL 5 MW baseline wind turbine 图3 导管架基础结构参数Fig.3 Parameters of jacket substructure 根据我国东南海域实测海况数据和表1所列的5 MW基准风机运行风速区间,为研究不同运行状态下海上风机的动力特性和TMD控制效果,依据GB/T 31517—2015规范[14]选取典型风、浪荷载组合,如表2所示.利用TurbSim[15]基于IEC Kaimal湍流模型生成脉动风速时程,基于JONSWAP 谱拟合得到随机波高时程,得到的风速和波高时程曲线如图4所示. 表2 设计荷载工况Tab.2 Design load cases (a) 风速 由海上风机-TMD两自由度体系计算模型计算得到单自由度海上风机结构一阶固有频率为0.318 Hz.TMD与海上风机结构的质量比取值范围一般为0.5%~2.0%[16].该样本海上风机M1为454 872 kg,本文拟定质量比为2.0%,则TMD质量为9 097 kg.拟定TMD刚度优化取值为30 000~150 000 N·m-1,阻尼优化取值为1 000~20 000 N·s·m-1.运用1.2节基于简化模型的TMD参数优化设计流程,经过20次迭代优化得到当TMD质量为9 097 kg时,对应的最优刚度和阻尼分别为Kd=35 666 N·m-1,Cd=2 527 N·s·m-1,迭代过程如图5所示. 图5 优化迭代过程Fig.5 Optimization iterative process 基于FAST建立空气动力-水动力-结构动力-控制系统整体耦合计算模型开展海上风机整体结构动力响应时域计算,具体如下: FAST主程序读入导管架式海上风机整体结构模型输入文件;将风速时程文件和海况文件分别导入脉动风模块和水动力模块,利用气弹分析模块和水动力模块进行气弹性和水动力分析,得到气动力荷载和水动力荷载;依据风机运行状态,伺服控制模块启动相应控制策略,在伺服控制模块里调用TMD程序进行结构振动控制;弹性动力模块和基础结构模块开展整体结构动力反应分析从而得到整体结构位移、内力等动力响应参数. 各设计工况下风、浪作用方向均沿图6所示整体坐标系x轴正方向.模拟总时长为630 s,计算步长为0.005 s.利用FAST在机舱内前后方向(图6所示整体坐标系x轴方向)建立一个单自由度TMD模型,主要包括质量、刚度和阻尼3个参数,并基于相关假定将弹性恢复力、阻尼力和惯性力的合力反作用于海上风机结构.上述耦合振动控制过程通过FAST中伺服控制模块TMD子程序[17]与弹性动力模块的耦合数值仿真计算来实现,FAST各模块的耦合分析流程如图7所示. 图6 导管架式海上风机整体坐标系示意图Fig.6 Schematic diagram of global coordinate system of the jacket-type OWT 图7 FAST海上风机整体耦合模型分析流程Fig.7 OWT fully coupled model analysis process in FAST 通过自由衰减测试工况验证基于海上风机-TMD两自由度简化模型并优化后的TMD减振控制效果沿塔筒顶部x轴方向施加1.0 m初始位移,得到有无TMD塔筒顶部位移时域、频域响应如图8、9所示.由图可知,优化后TMD有效地控制了以结构基频为主控频率的海上风机塔筒顶部位移自由衰减时程. 图8 塔筒顶部位移时域控制效果Fig.8 Control effects of tower top displacement in the time domain 本文选取4种代表性工况,以响应标准差减小率为评价指标研究被动控制TMD对不同运行状态下海上风机控制效果.为消除初始瞬态效应,去除前30 s数据进行统计得到响应标准差,按照式(9)计算得到各工况下响应标准差减小率,各工况最优TMD参数减振效果见表3. 表3 最优TMD参数减振效果Tab.3 Vibration reduction effect of optimal TMD parameters 图9 塔筒顶部位移频域控制效果Fig.9 Control effects of tower top displacement in the frequency domain (9) 式中:Δ为响应标准差的减小率,σ1为有TMD结构响应标准差,σ2为无TMD结构响应标准差. 海上风机塔筒顶部位移时域控制效果如图10所示.由图10并结合表3数据可知,额定风速以下工况1,TMD对塔筒顶部位移标准差减小率为0.33%;额定风速工况2,TMD对塔筒顶部位移标准差减小率为0.44%;额定风速以上工况3,TMD对塔筒顶部位移标准差减小率为1.51%;停机工况4,TMD对塔筒顶部位移标准差减小率为38.53%.综合各项评价指标可得,相对于正常运行工况,停机工况下TMD减振效果更为明显. (a) 工况1 各设计荷载工况下塔筒顶部位移频域控制效果如图11所示.由图可知,所选取正常运行工况1~3,塔筒顶部位移响应的控制频率包含风频、结构基频.而对于停机工况4,海上风机所采取的控制策略为叶片顺桨和高速传动轴制动,此时在风、浪荷载作用下,海上风机结构基频的影响效果明显大于风频,结构基频成为结构响应的最主要控制频率.同时,注意到该频率为TMD的调谐减振频率,故TMD在显著降低整体结构基频频域响应幅值的同时,也有效地控制了该工况下塔筒顶部位移运动响应.对于正常运行工况,虽然所设计TMD仍能有效控制整体结构基频幅值,但该工况下结构响应具有多个频率分量,并且整体基频影响明显弱于风荷载频率,由此削弱了正常运行工况下TMD减振效果. (a) 工况1 综上所述,本文所提出的海上风机-TMD两自由度简化模型,以塔筒顶部位移标准差为优化目标,利用人工蜂群算法得到优化后的TMD能够有效控制风、浪作用下停机状态导管架式海上风机结构的运动响应.但作为单频调谐控制方法,当海上风机结构响应主要控制频率与海上风机整体结构基频差异较大时,将明显削弱TMD的控制效果. (1)按照两自由度简化模型得到优化后的TMD,可使导管架式海上风机一阶模态顺风向塔筒顶部位移标准差减小率最大为38.53%. (2)由停机工况下TMD减振效果可得,塔筒顶部位移的主控频率为整体结构基频,所提出的海上风机-TMD简化优化设计模型合理,可用于开展针对海上风机一阶模态的TMD参数优化设计. (3)由正常工况下TMD减振效果可得,塔筒顶部位移的主控频率为风频,而该TMD针对结构基频而设计,所以对结构未起到明显的控制效果.

2 海上风机及设计工况
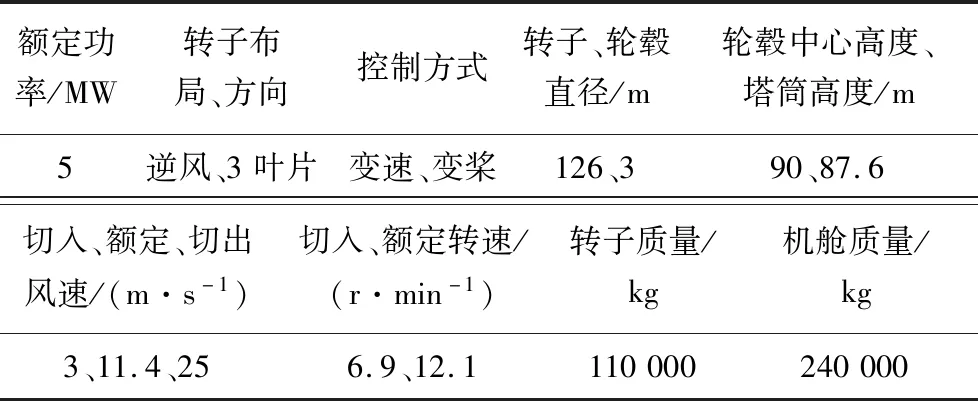
2.1 海上风机

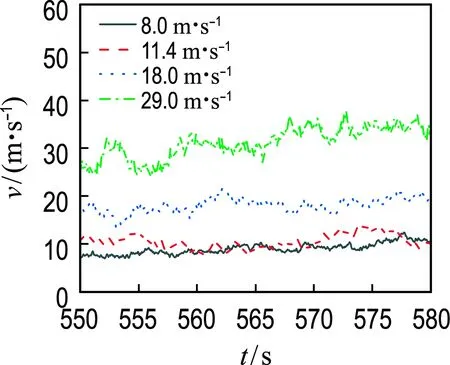
2.2 设计工况

3 优化设计TMD减振效果研究
3.1 FAST整体耦合计算模型


3.2 TMD参数验证

3.3 TMD减振效果研究


4 结 论

