新型自锚式悬索-连续梁组合体系人行桥理论分析及设计

卢 彭 真， 周 愉 涛， 李 登 国， 武 瑛

( 1.浙江工业大学 土木工程学院， 浙江 杭州 310014；2.嘉兴南湖学院 信息工程学院， 浙江 嘉兴 314001 )

0 引 言

人行桥(pedestrian bridge)，别名人行立交桥、天桥，通常修筑于行人与车辆密集区，或是露天广场、岔路口以及轨道交通上方．人行桥通常只允许行人通过(现允许自行车骑行的天桥也已开始逐渐流行)，可大幅度削弱车流平面及人流平面的冲突效应，降低事故的发生概率，在相当程度上保障行人的安全出行，同时也可有效提高车辆行驶速度，焕发城市活力．

随着生产力水平的提高，在复杂城市立体交通环境下，如何进行桥位合理布局、新材料和新结构的应用优化，从功能齐全、安全美观、环保耐久等多个角度开展人行桥的概念与结构设计是目前国内外学者关注的热点．以往的研究主要关注人行桥单一结构本身的力学行为[1]、使用功能[2]及其运营安全[3]等方面．在复杂有限的地形中如何布局与设计人行桥，并对设计桥梁进行全面优化的研究相对较少，这就导致目前城市多数人行桥呈现单一向、短跨径的形态．对此Lu等[4]基于国内天桥的发展历史与现状，运用现代化城市设计理念，提出了当代人行桥建设的发展趋势；Anderson[5]阐述了南非境内3座景观混凝土人行桥的设计发展．上述研究指出，随着城市的快速发展，在建的人行桥大多需要跨越6～12车道宽度的市政道路．若采取传统的设计方案，则需在施工阶段中断桥下交通．为确保施工和运营过程中既有交通的通畅与安全，势必要改进人行桥的设计．同时，由于城市规划中的非对称性，设计桥梁往往要跨越非对称地形地貌．基于此，在有限地形边界条件下如何修建安全、经济、美观、耐久及环保的人行桥成为城市设计和建设管理者面临的新问题．

目前，城市人行桥的建筑材料选择更加新型化，结构形式也日益多样化．其中钢箱梁结构具有自重相对较小[6]、可工厂预制现场焊拼[7]等特点，被认为具有快速装配、减小施工期间对既有交通干扰的潜力[8]；吊索结构具有柔性大、跨越强[9]、线形美、景观性好[10]等优点．因此吊索结构与钢箱梁结合形成的索-梁组合体系在城市人行桥的应用中具有较大的优势，已成为众多学者的研究主题[11-14]．然而，上述文献有关城市索-梁组合体系的研究对象均为标准的双塔单跨或双塔三跨，造价高昂，且并未考虑非对称性的情况，究其根本是现实中少有专门考虑有限城市空间非对称地形的桥梁设计实例．此外，为简化运算，多数现有悬索-连续梁组合体系以节线法索平衡状态方程的原理为基础[15]，即多采用竖直吊杆的形式，而这与非对称式天桥的设计及应用的契合度较低．因此，为实现有限地形条件下的人行桥设计，应对传统的悬索-连续梁组合体系展开进一步的结构优化．

针对上述问题，本文提出大跨度单塔单肢空间自锚式悬索-连续扁平钢箱梁组合体系人行桥的概念，以解决目前城市人行桥面临的两大问题：(1)施工期间中断桥下繁忙交通；(2)城市有限空间非对称地形下的人行桥布局．为保证新提出的异形空间组合桥梁系统的可行性，本文研究新组合体系的结构力学行为，采用有限元理论建立FE模型，全面揭示该体系的静力行为、动力性能及稳定性．基于全面的模拟分析结果，为改善其力学性能，提出曲梁内嵌和梁上主缆锚固点的水平分力由桥台承担及边跨主梁承担轴向拉力的方法．同时，组合体系设计尝试性地采用斜拉式吊杆的形式以改善结构的动态性能，并通过步行激励荷载的模拟，对该人行桥进行必要的减振设计．进一步地，运用MOGA对新型悬索-连续梁组合体系的人行桥进行优化设计，使该结构布局更加合理、受力更加安全、建造更加经济、使用更加耐久，为该组合体系在未来人行桥设计中的推广应用提供理论依据和工程实践经验．

1 单塔单肢空间自锚式悬索-连续扁平钢箱梁组合体系人行桥

1.1 组合体系人行桥概念

针对组合体系的人行桥，国内外已经有不少桥梁工程项目证实了典型的索-梁-塔组合体系的有效性．例如，坐落于厦门大学校门口的圆弧形白城人行桥(图1(a))，用斜拉索结构配合斜塔呈现出优美的空间曲线；德国波鸿加仑索大街的S形人行桥[16](图1(b))，也充分证实了空间桥梁设计的可行性．基于索-梁体系人行桥的设计案例，本文提出了单塔单肢空间自锚式悬索-连续扁平钢箱梁组合体系人行桥初步概念及其优化设计的构想．该结构将边跨设置成连续梁体系，主跨设置为组合体系，桥塔采用梭形倾斜形式，索体一端锚固在主梁上，另一端锚固在地面上，且索形转化为空间抛物线形(图2(d))．该体系将传统平面化的悬吊系推向空间三维化，为组合体系的创新做出了显著的空间拓展．在空间布局上，通过边跨的连续梁体系可跨越复杂地形，主跨组合体系可跨越宽河道或大型市政道路，为主跨下的水路或陆路运输提供充足的垂直间隙．

图1 典型组合体系人行桥Fig.1 Pedestrian bridge with typical composite system

1.2 组合机制

为实现两种体系之间的合理组合，钢箱梁板可分为4个部分：桥台段的连续变截面梁，一段长直箱梁，人字分叉前的连续变截面梁，分叉后的两段弯曲梁．考虑悬索桥特性，组合段箱梁的截面几何刚度要大于连续梁段箱梁的刚度；考虑到异形桥特性，分叉后的弯曲梁扭转刚度应大于长直梁段．为使连续梁段获得足够的刚度并充分调动悬索结构的作用，对连续梁段的中间两个墩作固接处理．同时采用新式的索塔结构：利用球铰(图2(a))控制整体桥形并降低振动效应；使用两对双耳板(图2(b))加强主缆、背索和桥塔的刚接．为使悬吊系与钢箱梁有效结合，对自锚点处钢箱梁作如图2(c)所示固接外伸装置，同时对吊杆的起吊点也作类似的外伸固接装置．其中钢结构锚固区采用铸焊结合，内钢板布设焊钉并填筑混凝土，以分散局部应力；两侧主传力钢板与主梁腹板纵向对应，以保证传力直接顺畅；同时，设置传力过渡段，对该区域箱梁顶板及底板等构件进行适当加强，防止锚点处的局部失稳破坏．组合体系的受力解析如图2(d)所示．

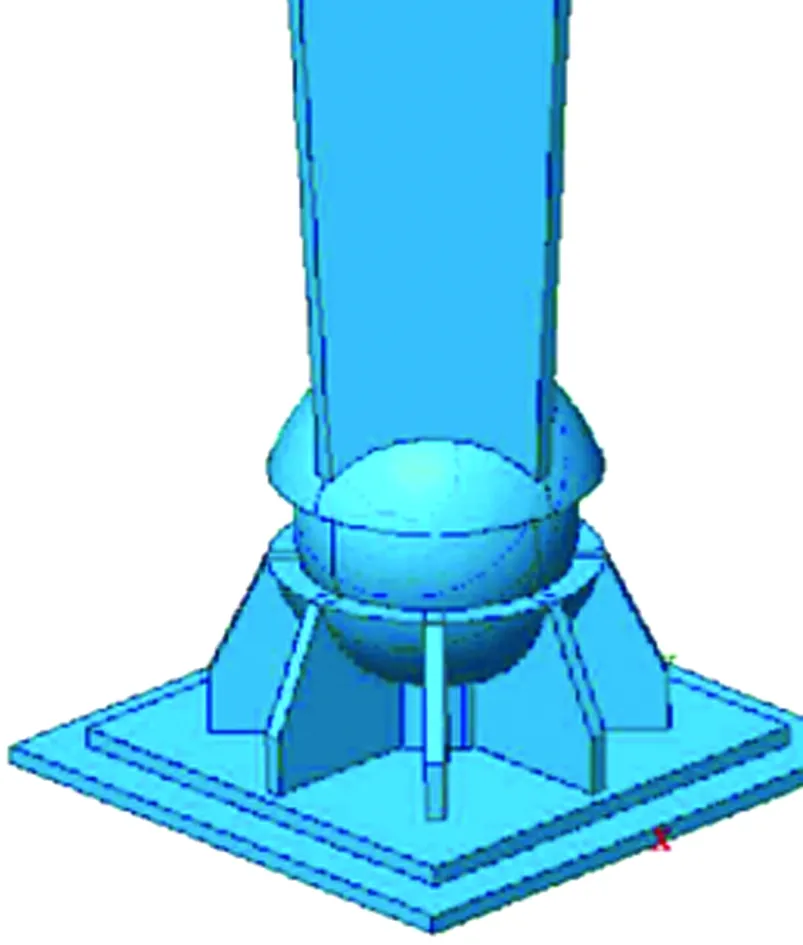
(a) 球铰结构

2 组合体系人行桥结构力学行为

2.1 有限元模型的建立

为验证新体系的实用性，依据新组合体系人行桥的概念，对某健康步道景观提升工程的5号节点人行桥进行设计．该节点桥起点位于薛岭山公园，连接现状步道，连续跨越市区绿化中心绿化枝叶粉碎场及市区主干路金尚路(主车道双向6车道)，终点位于虎头山公园，连接现状步道(桥址状况如图3所示)．

图3 桥址平面图(单位：m)Fig.3 Plan of the bridge site (unit: m)

使用Midas/Civil软件对该组合体系人行桥进行了FE模型的建立，以初步研究分析其受力性能，分析模型如图4所示．本次Midas建立的模型真实模拟桥梁结构尺寸，共建立264个节点，246个单元．其中主缆和吊杆的直径分别定义为70 mm和22 mm，并设置为索单元．梁、塔、墩均以梁单元形式构筑．其中梭形桥塔使用的塔中断面和塔顶/底断面如图5所示，其余截面按圆曲线渐变内插；主梁纵桥向坡度为2.74%，分析采用的典型钢梁截面见图6．本桥主梁、墩柱及桥塔均采用Q345B钢材，泊松比0.3，弹性模量206 GPa；通体采取焊接形式，焊条采用E50；主缆和背索采用镀锌高钒索，抗拉强度1 860 MPa；吊杆采用不锈钢绞线拉索，抗拉强度1 300 MPa．边界条件方面，P0塔台铰接，P1、P2与梁体固接，P3、P4、P5、P6设置支座，T0塔台铰接，T1、T2地锚固接，梁单元与索单元之间均采用刚性连接．基于上述构建的FE模型进行初步的静态及模态分析．根据新体系初步分析结果中暴露出的设计问题，利用多目标遗传算法(MOGA)对结构进行优化设计，实现组合体系设计的最佳解决方案．

图4 人行桥有限元模型Fig.4 Finite element model of pedestrian bridge

(a) 塔顶/底断面

图6 主梁典型截面(单位:mm)Fig.6 Typical section of main beam (unit: mm)

2.2 静态分析

首先，分析该组合体系的静力学特性．在静力分析的状况下，行人和移动重物引起的垂直荷载被定义为外部活荷载．分析AASHTO(1997)[17]、CEN(2004)[18]、BS 5400-2(2006)[19]、CJJ 69—1995(1996)[20]、JSSC(1998)[21]等规范，大多数国家人行桥的推荐活荷载取值范围为3～5 kPa．鉴于中国规范CJJ 69—1995中明确了严格的计算公式，参考其具体条例进行人群荷载初值计算．

当加载长度为21～100 m(100 m以上同100 m)时：

(1)

式中：W为单位面积的人群荷载，kPa；L为加载长度，m；B为半桥宽度，m，大于4 m时仍按4 m计算．

本次设计中加载长度为70 m，故可得出下式：

3.4 kPa

(2)

得出的人群荷载W恰好落在3～5 kPa的区间内，因此采用人群荷载3.4 kPa．且3.4 kPa相当于1 m2区域内站着5名68 kg的成年人，对于该桥梁的一般使用阶段，其实际活荷载应远低于此值．故而取人群荷载3.4 kPa是偏于安全的．在选择该活荷载大小的情况下对组合体系人行桥进行静力分析．参考CJJ 69—1995对组合体系人行桥进行了两种情况的荷载组合分析．

(1)组合1：结构自重(一期自重系统自动生成，二期恒载设为1.25 kN/m)．

(2)组合2：结构自重、活荷载、系统升温、正温度梯度、不均匀沉降与风荷载．

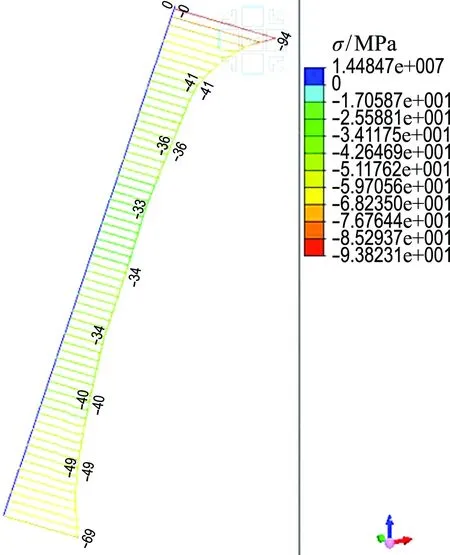
两种组合下组合体系人行桥结构梁单元的弯曲与剪切应力以及悬吊系内力与桥塔应力如图7～9所示．

(a) 组合1主梁上缘应力图

(a) 组合2主缆最大轴力

(a) 组合2桥塔最大应力图

组合1可模拟该组合体系人行桥的成桥阶段，此时人行桥位移量为0；钢梁上缘最大压应力42×1.1 MPa=46.2 MPa，最大拉应力55×1.1 MPa=60.5 MPa；下缘最大压应力51×1.1 MPa=56.1 MPa，最大拉应力67×1.1 MPa=73.7 MPa．可见人行桥成桥应力较小．组合2可模拟该组合体系人行桥的长期使用状况．在此组合情况下主缆达到最大轴力2 235×1.1 kN=2 458.5 kN，吊杆达到最大轴力119×1.1 kN=130.9 kN．基于二阶分析观察分叉后的两段弯曲梁出现了较为明显的扭转变形，这是由于索梁组合段在荷载组合2作用下存在较大的柔性位移，该位移达到284 mm，导致该弯曲梁在分叉端也产生了接近100 mm的竖向位移，这意味着整片曲梁的最大扭转角可达6.84°，导致扭曲的钢箱梁横截面的中心斜率近12%，这是弯曲变形和扭转变形的耦合作用．从数值上看，组合2作用下的主梁应力较之组合1有了较大的提高，但是全桥的应力趋势较为相近，说明在各荷载组合作用下起决定性作用的还是结构自重，且人群荷载作用的趋势和结构自重相近．

基于上述静力分析的结果，一种可行的优化人行桥静力特性的方案是将整片曲梁整体向变截面梁体中内嵌一部分，加强结构在分叉点的刚度，通过设计连接件使得非扭转的长直箱梁与弯曲梁的连接接头处的轴向力得到释放，这样也就活用了整座桥五跨一联的布局形式．同时由于主缆锚固点的水平分力由桥台承担，边跨主梁承担轴向拉力，整体变形量都会得到降低，结构应力也得到明显降低．

2.3 模态分析

2.3.1 稳定性分析 本桥为人行桥，采用了全钢结构，故其稳定性问题突出，需进行稳定性检验．按空间体系验算，运营过程中该桥属于一类稳定问题，根据BS 5400、《公路钢结构桥梁设计规范》(JTG D64—2015)[22]等标准确定本体系桥梁稳定系数需大于4～6．该人行桥失稳分析如图10所示．经检验，该组合体系人行桥的稳定性满足设计要求．

同时分析了结构各关键位置处的局部稳定性．以吊点为例，采用ABAQUS软件建立吊点模型，进行屈曲分析，如图11所示．可知，增设纵向和横向支撑板可提高吊点稳定性．经检验，全桥各压弯构件的稳定性良好，均满足设计要求，保证了局部失稳不先于整体失稳发生．

(a) 桥墩初次失稳(特征值11)

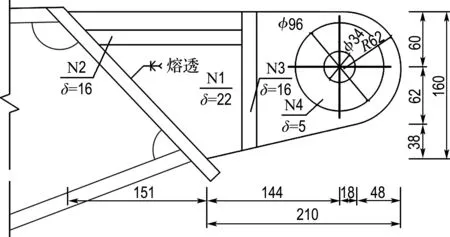
(a) 吊点加固方案示意图

2.3.2 减振初步分析 轻质高强材料的充分运用导致人行桥的静力性能在不断优化的同时，固有频率却在持续下降．人群行走激励作用将导致低频人行桥产生较大振幅，不但影响桥上行人的步行舒适感，甚至会诱发人行桥的结构安全问题．国内结构振动舒适度的研究正处于逐步成型阶段，而国外在该方面已有多年深入的研究[23-25]．典型的加速度峰值评价标准如表1所示．在分析国内外各规范的情况下，本桥采用0.05g为人行桥竖向加速度限值，0.025g为人行桥横向加速度限值，确定了本组合体系在振动分析时的舒适度评价标准．通过模拟分析，新体系人行桥结构的前10阶振型和固有频率如图12所示．

(a) 一阶振型 0.84 Hz

表1 常用的加速度峰值评价标准Tab.1 Commonly used evaluation criteria of peak acceleration

采用同步激励荷载作为移动的随机人群荷载，模拟行人在1.60、2.08和1.82 Hz 3种频率下的同步行走．具体分析详见文献[30]．结果表明，在1.60 Hz相应的步行激励作用下，人行桥竖向共振效应较弱，竖向加速度峰值为0.21 m/s2(约0.021g)，能够满足使用要求，暂不需要采用减振措施．而在2.08 Hz和1.82 Hz相应的步行激励作用下，竖向和横向加速度峰值分别为0.80 m/s2和0.27 m/s2，人行桥共振效应明显，不能满足使用要求，均需采取减振措施．

阻尼减振是桥梁减振的重要设计方法[31]，为验证阻尼减振对新体系的适用性，在该人行桥中安装调谐阻尼减振器(TMD)，通过分析减振后的振动加速度响应，判断TMD减振效果．行进频率2.08 Hz对应桥梁五阶自振频率2.08 Hz，人行桥主质量约163.5 t，取μ=0.04，则TMD的设计总质量为6.5 t，分设4台TMD以避免应力集中；行进频率1.82 Hz，二阶自振频率0.91 Hz，人行桥主质量214.3 t，取μ=0.015，则TMD的设计总质量为3.2 t，分设2台TMD．每个TMD质量为1.5 t，布置在主跨四分点附近．

施加人行激励荷载，人行桥跨中42号节点的竖向和横向振动加速度响应分别如图13(a)和(b)所示．安装4台竖向TMD和2台横向TMD后，减振效果明显．其中竖向减振效果40%(0.80 m/s2→0.48 m/s2)，横向减振效果22.2%(0.27 m/s2→0.21 m/s2)．可见合理安装TMD是解决新体系动态变形的有效方案．

(a) 竖向(2.08 Hz)

3 组合体系人行桥的优化设计方法及应用

通过将新组合体系与实体人行桥的设计相结合，论证该组合体系在非对称地形条件下人行桥设计中的有效性．但为了进一步探究该结构在各种地形上设计的可行性，提出了采用基于MOGA的结构优化方式来锁定不同场合下该组合体系的结构最佳形状．通过形状优化获得不同情况下的最优设计参数，可突破传统设计过程中耗力耗时的反复实验试错过程．

3.1 优化算法

GA及其延伸算法受自然选择中交叉变异的启发，已成为人工智能设计分析的一项重要分支．目前GA已日臻成熟并广泛运用在结构工程中[32]．MOGA是基于GA的一种进阶算法[33-34]．但由于多目标问题的复杂性，其在工程领域还未形成体系化应用，因此仍在持续发展中[35]．本文借鉴MOGA，提出了该算法在组合体系结构优化中的可行性．

MOGA可以看作遗传算法和结构分析的融合，多目标优化问题的一般数学模型可描述为

min {f(x)=(f1(x)f2(x) …fj(x))T}

x∈X

X⊆Rm

(3)

在数学意义上，若有解x1，x2∈X，且任意k=1，2，3，…，都有fk(x1)≤fk(x2)，则称解x1比x2优越；但当解x1不能使全体fi(x)均完成最优化，但不存在比x1更优越的解xp时，则称x1是应用多目标优化模型在数值上的Pareto最优解．运用MOGA求解Pareto最优解，令全体种群A按子目标函数的数目j等分为j个子群体a1、a2、…、aj，并对每一个子群体ai均分配一个目标函数，用以择优，通过各自的目标函数分别筛选出各个目标区间内具有较高适应性的子个体共同组成一个新的子群体bi⊆{b1，b2，…，bj}，然后将上述全体bi整合为一全新种群B={b1，b2，…，bj}，在这个群体里进行繁殖，繁殖期间进行交叉变异的自然择优，产生下一代完整群体C，如此循环上述3段过程，最终生成该种群A期望达到的模型上的Pareto最优解种群Z．本文采用的MOGA进一步采用保留Pareto 最优个体的方法，即直接将对于子群体中的Pareto最优个体保留到下一代的子群体中，而不让其参与B到C的交叉变异中，大幅压缩了运算时间．具体优化过程的流程如图14所示．

图14 MOGA优化过程的流程图Fig.14 Flow chart of MOGA optimization process

3.2 应用案例

以某健康步道景观提升工程的5号节点桥为例，首先定义人行桥的形状参数s1(定义桥梁的整体性预期形状尺寸．以本例而言，主要包括起点高程h1、终点高程h2、边跨数量n、边跨长度l1、组合段长度l2、曲梁段转角φ、曲梁段半径R)和边界参数s2(定义控制桥梁设计的边界条件相关变量．对于本例主要包括桥塔球铰X、主缆L、自锚点Y1、地锚点Y2、固接墩P、普通支座Z等)．

s1=(h1h2l1nl2φ1φ2R1R2)

(4)

s2=(XL1L2Y11Y12Y21Y22P1P2

Z1Z2Z3Z4Z5Z6)

(5)

s1的初始值由条件决定，其取值如表2所示(初始参数的取值将影响迭代计算的收敛速度和效率．由于存在多个Pareto最优解，它可能会收敛到其他局部最优结果，这取决于初始参数)．MOGA参数如表3所示．随后，通过算法进行优化处理，最终该人行桥的最佳形状参数如表2所示．

表2 初始及优化后的形状参数s1Tab.2 Initial and optimized shape parameter s1

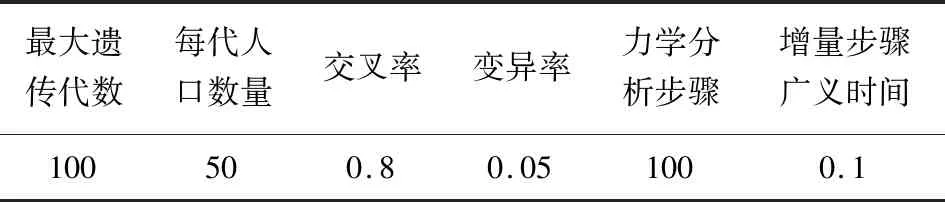
表3 MOGA参数Tab.3 Parameters of MOGA

优化形状参数后重新建立有限元模型，分析其力学行为，结果如表4所示．由表可知，经过MOGA优化后的组合体系人行桥在荷载组合2作用下的主梁最大挠度减小了33 mm，一/二阶竖弯频率及一阶侧弯频率均有所提高，说明经过优化，全桥刚度得到一定程度的提升．进一步地，通过施加随机行人荷载计算一/二阶竖弯频率及一阶侧弯频率相应的步行激励作用下的人致振动响应．可知经MOGA优化后，桥梁一/二阶竖向及一阶侧向对应的振动响应(无安装阻尼器)分别下降了14.3%、22.5%和18.5%．上述分析证实，经MOGA优化后人行桥结构的静力和动力性能都得到了进一步改善．

表4 优化前后人行桥的力学行为Tab.4 Mechanical behavior of pedestrian bridge before and after optimization

4 结 论

(1)基于三维空间中的弹性变形与刚体扭转的组合机制，该组合体系采用了新式的连接件进行索、梁、塔的三位一体连接组合．有限元分析显示该体系静力性能良好．

(2)提出了曲梁内嵌和梁上主缆锚固点的水平分力由桥台承担及边跨主梁承担轴向拉力的方法，该方法可减小结构变形与应力，有效解决该体系在实际工程运用中可能遭遇的曲梁扭转问题．

(3)提出了该组合体系的振动舒适性评价标准，初步分析了人行桥人致振动响应．针对人致振动响应显著的问题，采用竖向、横向TMD减振设计方法，证明TMD对结构减振具有良好的适用性．

(4)提出的新组合体系适用于有限城市空间非对称地形条件．引入MOGA对新组合体系进行结构优化调整，优化后人行桥结构的静力和动力性能都得到了进一步的改善．

(5)本文所提出的自锚式悬索-连续梁组合体系可为今后复杂地形边界条件下的人行桥设计及其结构优化提供借鉴．

由于本文对新组合体系的力学行为仅进行了初步分析，后续应根据实际应用展开进一步研究，如异形荷载的力学分析(不同方向的风力作用和地震作用)、新组合体系在不同程度非对称条件下的应用等．