计及UPFC的主动配电网日前-实时优化策略
曹宏基,刘道兵,李世春,金梓桐,樊 煜,鲍志阳
(1.国网湖北鄂州供电公司,湖北鄂州 436001;2.三峡大学电气与新能源学院,湖北宜昌 443002;3.国网湖北随州供电公司,湖北随州 441300)
0 引言
发展分布式电源是我国电力行业发展的重要举措[1],对传统配电网规划和运行提出了新的挑战,促使传统无源配电网向具备潮流主动控制能力和与负荷互动能力的主动配电网(Active Distribution Network,ADN)转变[2-3]。研究ADN 的调度优化问题有利于减小电能损耗,达到节能降耗的目标[4-6];统一潮流控制器(Unified Power Flow Controller,UPFC)具有电压调节、移相、阻抗补偿和综合控制等功能[7-8];充分发挥UPFC 调控能力可以提高电网运行的安全经济性[9-10]。因此,研究UPFC 在ADN 中的应用具有理论与实践意义。
微型燃气轮机(Micro-Turbine,MT)运行具有时序耦合性:两相邻时段之间输出的有功功率相互关联。文献[11]分别建立了以输出有功和视在功率最小为目标的UPFC 优化控制策略,对1 个时间断面的优化效果进行了分析。文献[12-13]通过UPFC 协调控制配电环网的节点电压、网络损耗,未考虑时序耦合特性,仅为单时段优化。另外,实时优化对计算时间要求较高,而UPFC 非线性模型使优化策略只能使用智能算法求解,计及时序耦合特性进行滚动求解不利于优化,容易早熟,高维度下收敛时间漫长。文献[14]通过多维动态规划方法将ADN调度优化策略模型时序解耦,但多维动态规划的使用前提限制了其使用,亟需寻求其它时序解耦的实时优化方法。
针对实时阶段计及时序耦合特性不利于含UPFC 的优化策略模型求解的问题,本文提出计及UPFC 的ADN 日前-实时优化策略。建立分层优化策略:通过不考虑UPFC 的ADN 日前线性优化模型确定实时调度的MT 调节幅度上、下限。下层为单时段实时优化模型,在加入UPFC 进行优化控制的同时计及UPFC 损耗;由于UPFC 使网损下降以及新能源出力、负荷预测的偏差,需调整日前调度策略,重点改进MT 模型,使单时段实时优化无需考虑其时序耦合特性,通过智能算法求解实现全局优化。最后,采用IEEE33 节点主动配电网算例仿真,验证所提方法提升了实时优化求解速度与收敛性。
1 UPFC模型
本文采用的UFPC 模型的一个逆变器(Voltage Source Converters,VSC)经变压器串联在交流线路中,另一个VSC 通过变压器并联于节点,2 个VSC通过直流母线电容相连[15],UFPC 模型的结构如图1所示。UFPC 安装在ADN 线路上,通过串联侧和并联侧变压器改变线路的潮流的同时,也能提供或吸收无功功率。

图1 UPFC模型结构Fig.1 UPFC model structure
为方便建模,假设ADN 连接主网的节点为根节点,UPFC 只安装在每一条支路的父节点侧,Pij0,t,Qij0,t分别为t时刻UPFC 在支路ij的节点i侧产生的 有 功功率、无功功率;Pij1,t,Qij1,t分别为t时刻UPFC 在支路ij的节点j侧产生的有功功率、无功功率;Pr,ij,t为t时刻支路ij的节点i侧注入UPFC 并联侧变压器的有功功率;Pr1,ij,t为t时刻注入支路ij上UPFC 的VSC1 的有功功率;Pr2,ij,t为t时刻支路ij上UPFC 的VSC2 输出的有功功率;QVSC1,ij,t,QVSC2,ij,t分别为t时刻支路ij上UPFC 的VSC1,VSC2 的无功功率;Zij为线路ij的阻抗;Ui,t,Uj,t分别为t时刻i,j节点的电压。
在ADN 运行优化计算中可忽略对地导纳[16],因此,文献[17]忽略对地导纳后,UPFC 在线路上的功率模型为:
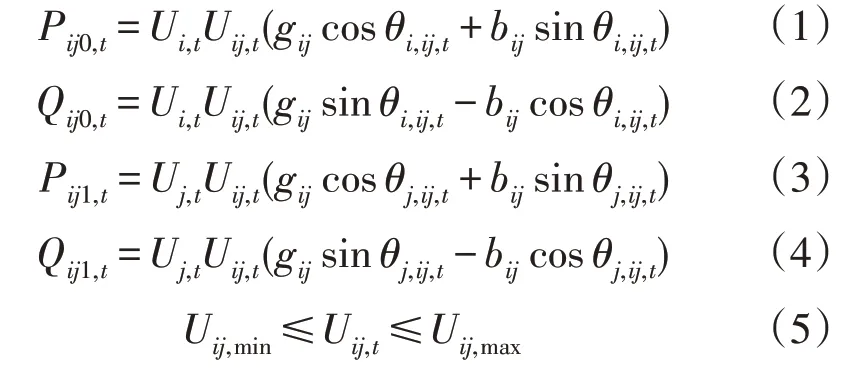
式中:Uij,t为t时刻支路ij的UPFC 串联侧等效电压源的电压幅值;Uij,min,Uij,max分别为支路ij的UPFC 串联侧等效电压源的最小、大值;gij,bij分别为线路ij的电导、电纳;θi,ij,t为t时刻节点i的电压相角与支路ij上串联侧等效电压相角的差值。
UPFC 串联侧变压器的功率平衡方程为:
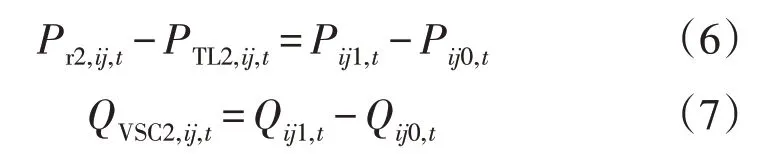
式中:PTL2,ij,t为t时刻支路ij上UPFC 串联侧变压器损耗。
UPFC 并联侧变压器的有功功率平衡方程为:

式中:PTL1,ij,t为t时刻支路ij上UPFC 的并联侧变压器损耗。
变压器损耗包含的可变损耗和固定损耗为:

式中:RTL1,ij,Ue1,ij,P0T1,ij分别为支路ij上UPFC 并联侧变压器的等值电阻、额定电压、空载损耗;RTL2,ij,Ue2,ij,P0T2,ij分别为支路ij上UPFC 串联侧变压器的等值电阻、额定电压、空载损耗;kTij为支路ij上串联侧变压器阀侧与网侧电压比。
二VSC 的有功平衡方程为:
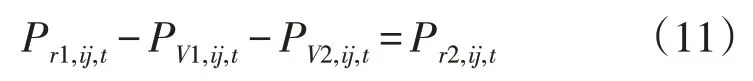
式中:PV1,ij,t,PV2,ij,t分别为t时刻支路ij上UPFC 的VSC1,VSC2 的损耗。
VSC 损耗为:

式中:AV1,ij,AV2,ij分别为支路ij上UPFC 的VSC1、VSC2 的损耗系数。
VSC 容量由流过的有功、无功功率共同决定,其约束条件为:

2 日前优化模型
日前优化不计及UPFC,通过各时段MT 出力确定实时优化的MT 出力调节范围,以确保实时优化阶段MT 出力能满足全时段优化要求。
2.1 目标函数
本文中分布电源只考虑MT、风机(Wind Turbine,WT),运行成本包含网损、与上级电网交互、需求响应、MT 发电成本。即:
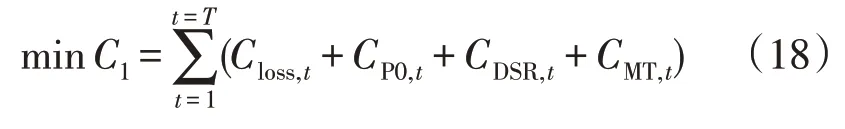
式中:C1为日前优化策略目标函数;Closs,t为t时刻网络损耗成本;CP0,t为t时刻与上级电网交互成本;CDSR,t为t时刻需求响应的成本;CMT,t为t时刻MT 发电成本;T为调度周期。
1)网损为:

式中:lij,t为支路ij在t时刻电流的平方;Rij为支路ij的电阻;ω为售电价格;E为ADN 的线路集合;tΔ为时段长度。
2)与上级电网交互成本为:
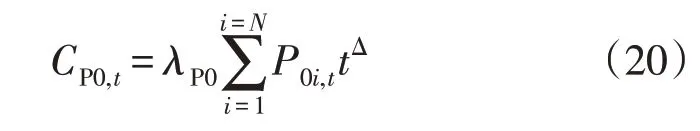
式中:λP0为ADN 与上级电网交互单位功率的价格;P0i,t为t时刻节点i与上级电网交互有功;N为ADN的网络节点个数。
3)需求响应侧成本为:

式中:λCUT为削减负荷的价格;PCUTi,t为t时刻i节点负荷削减量。
4)MT 发电成本包含燃料[18]和VSC 损耗成本。则MT 发电成本为:

式中:λMT为MT 单位发电的燃料成本;PMTi,t为t时刻i节点MT 的有功功率;PMTV1i,t,PMTV2i,t分别为t时刻i节点MT 侧、网侧VSC 的损耗。
2.2 约束条件
1)MT 约束
MT 出力约束为:
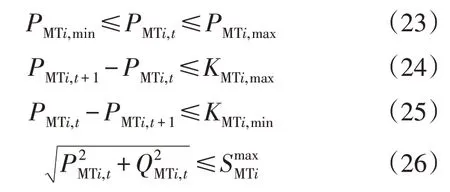
式中:PMTi,min为i节点MT 有功出力的下限;PMTi,max为i节点MT 有功出力的上限;QMTi,t为t时刻i节点MT的无功;为i节点MT 的视在功率;KMTi,max为i节点的MT 有功出力的爬坡上限(值大小为正);KMTi,min为i节点的MT 有功出力的爬坡下限(值大小为负)。MT 功率入网需经过VSC[19],其结构如图2 所示。

图2 MT入网结构Fig.2 Connection structure of MT and network
VSC 损耗为:

式中:AMT,i为i节点MT 的VSC 损耗系数;PMTGi,t为t时刻i节点MT 的入网有功。
VSC 损耗模型可转化为二阶锥形式:
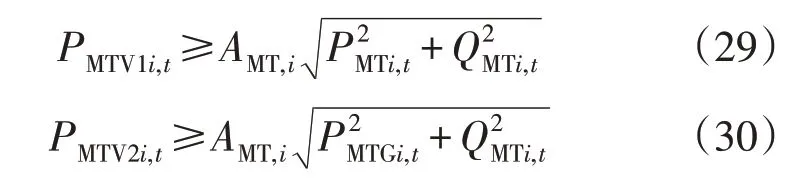
入网功率平衡方程为:
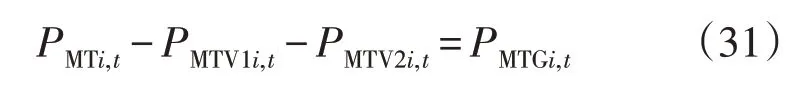
另外,还包含VSC 容量约束,文中假设VSC 容量大于MT 容量。
2)WT 出力约束
WT 有功出力为预测值,无功出力约束为:
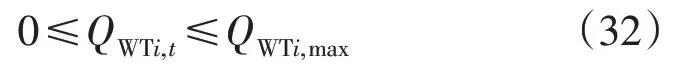
式中:QWTi,t为t时刻i节点WT 无功出力;QWTi,max为i节点WT 无功出力上限。
3)节点注入功率约束。

式中:Pi,t,Qi,t分别为t时刻注入节点i的有功、无功;Q0i,t为t时刻节点i与上级电网交互的无功;PLi,t,QLi,t分别为t时刻节点i的预测有功、无功负荷;PWfi,t为t时刻节点i的WT 出力预测值。
4)潮流、节点电压、支路电流约束。文献[20]介绍了潮流、节点电压、支路电流约束。
5)负荷削减、与上级电网交互功率约束。文献[21]介绍了负荷削减、与上级电网交互功率约束,只限制其上、下限。负荷削减、与上级电网交互有功、无功下限为0。
3 实时优化模型
实时优化计及UPFC,由于UPFC 使得网损下降以及新能源出力、负荷预测的偏差,需重新确定运行方案,非时序耦合变量可直接优化,时序耦合的MT 有功变量调整范围由日前方案确定。
3.1 目标函数
实时优化目标函数包含日前的单时段优化目标、UPFC 损耗。即:
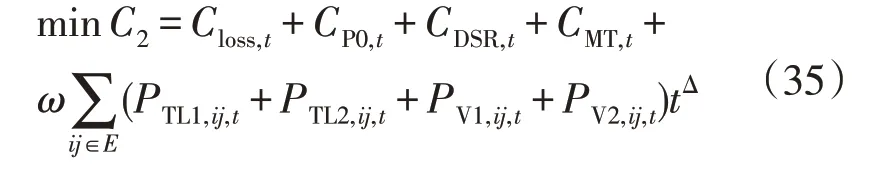
式中:C2为实时优化策略目标函数。
3.2 约束条件
1)节点注入功率约束为:

式中:N(i)为节点i的子节点集合;分别为t时刻节点i的实时有功、无功负荷;PWri,t为t时刻节点i的WT 实时出力。
2)功率平衡约束为:

式中:Xij为支路ij的电抗。
3)潮流约束。UPFC 的串联侧电压影响了支路潮流。即:

式中:Gij,Bij分别为节点i,j之间的互电导和互电纳;M(i)为节点i的父节点集合;Ω(i)为与节点i相连的线路集合;θij,t为t时刻线路ij的电压相角差。
4)节点电压约束为:
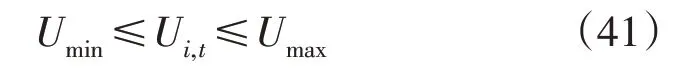
式中:Umax,Umin分别为节点电压最大和最小值。
5)支路电流约束。其中,不含传统UPFC 的支路电流约束为:
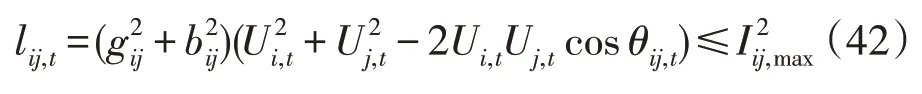
式中:Iij,max为支路ij的电流最大值。
含传统UPFC 的支路电流约束为[22]:

式中:θi,t为t时刻i节点电压相位。
6)MT 约束。MT 有功出力时序耦合,单时段优化时,需确保上一时段MT 实时出力能到达当前优化时段MT 出力,以及当前优化时段MT 出力能到达下一时段MT 日前调度出力。
因此,对MT 模型进行改进,首先,需确定当前、下一时段MT 的爬坡幅度,再通过爬坡幅度确定当前时段MT 相对前后二时段的有功调节幅度上、下限,最后,综合MT 有功出力范围确定当前时段MT的向上、下调节幅度。其逻辑结构如图3 所示。
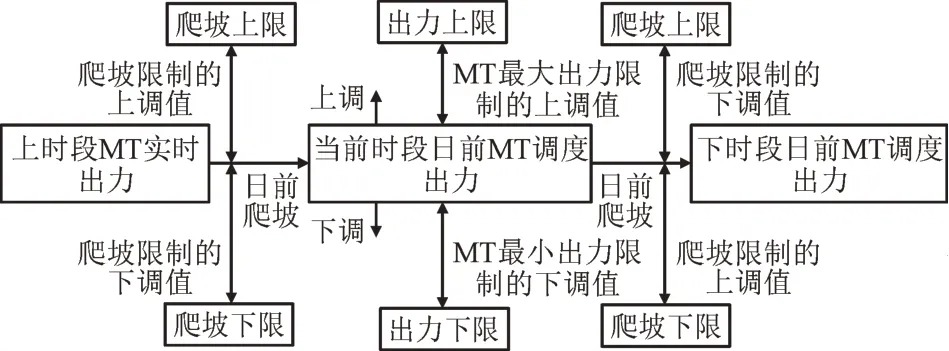
图3 改进MT的逻辑结构Fig.3 Logical structure of improved MT
当t=1 时,当前MT 的爬坡幅度为:

式中:ki,1为初始时段i节点MT 的爬坡幅度。
当t>1 时,通过上一时段MT 实时出力、当前时段MT 计划出力,计算得到当前MT 的爬坡幅度为:

通过日前下一时段、当前时段MT 计划出力,计算得到下一时段MT 的爬坡幅度为:

当t=24 时,假设24 时MT 计划出力与第2 天1时出力爬坡幅度为0,其约束为:

当前MT 下调时,相对上时段MT 为出力下调,下调值受爬坡下限影响;而下时段MT 出力相对当前出力等效为出力上调,当前MT 下调值受爬坡上限影响。计算当前MT 相对上时段MT 的向下调节幅度为:

计算当前MT 相对下一时段MT 的向下调节幅度为:

MT 有功出力下限限制的向下调节幅度为:

当前时段MT 向下调节的值为负,且需同时在式(48)—(50)范围内,因此,取三者最大值作为当前时段MT 的向下调节幅度,即:
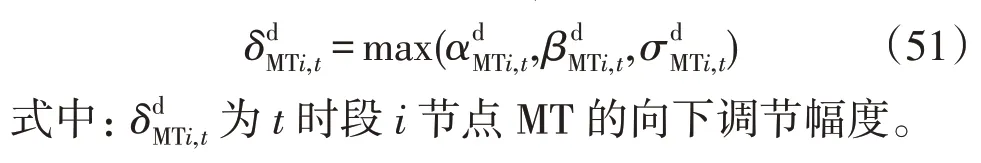
当前MT 上调时,相对上时段MT 为出力上调,上调值受爬坡上限影响;而下时段MT 出力相对当前出力等效为出力下调,当前MT 上调值受爬坡下限影响。计算当前MT 相对上一时段MT 的向上调节幅度,即:
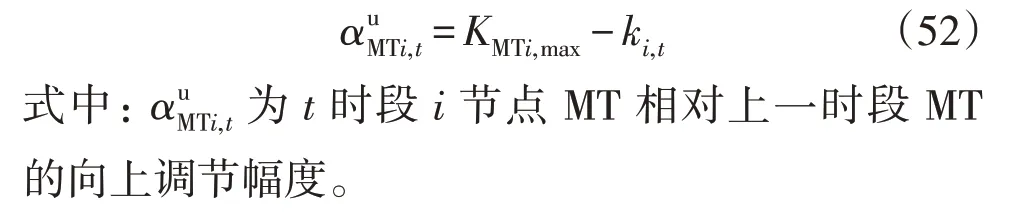
计算当前MT 相对下一时段MT 的向上调节幅度,即:

MT 有功出力上限限制了向上调节幅度:
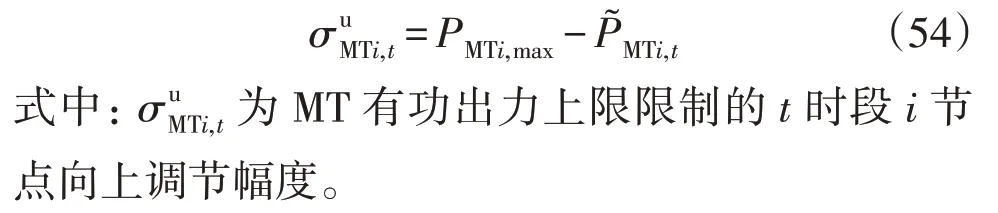
当前时段MT 向上调节的值为正,且需同时在式(52)—(54)范围内,因此,取三者最小值作为当前时段MT 向上调节幅度,即:

引入MT 出力调整变量εMTi,t,其变化范围由当前时段向下、上调节幅度确定为:

式中:εMTi,t为t时段i节点MT 出力调整量。MT 有功、无功约束为:
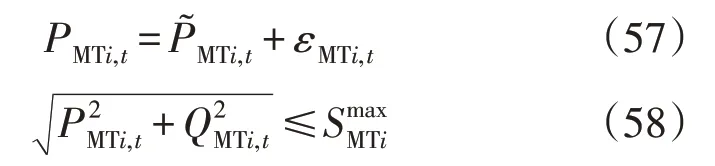
MT 的VSC 损耗同式(27)—式(28),入网功率同式(31)。
另外,WT 有功为实时值,无功约束同式(32);负荷削减、与上级电网交互功率约束同2.2 节;UPFC 约束同式(1)—式(17)。
4 模型求解
本文日前优化模型为一个混合整数二阶锥规划问题,采用优化规划软件Mosek 进行求解仿真,通过确定实时阶段MT 调节范围实现断耦合,降低实时优化智能算法求解维度,以提高运算速度与收敛性。
实时优化模型是一个多变量多约束非线性优化问题。利用遗传算法求解ADN 实时优化调度模型。考虑MT 出力的时序解耦后,实时优化变量减少,有利于遗传算法的收敛。实时优化求解过程如图4 所示。运算过程中,通过罚函数保证筛选的变量值满足约束条件。
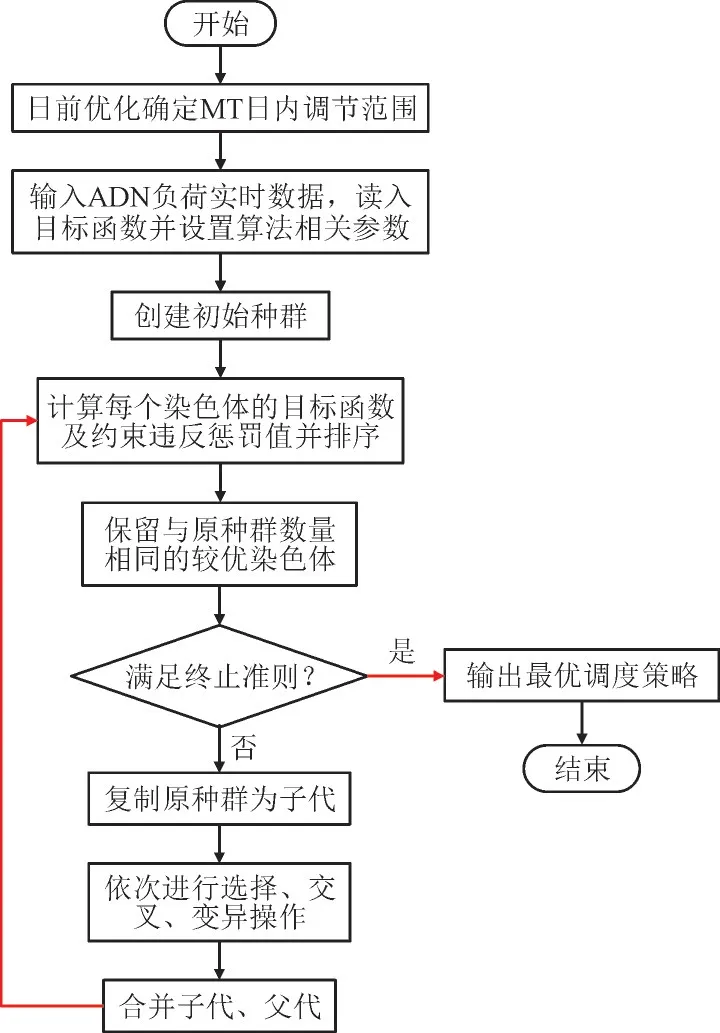
图4 求解过程Fig.4 Solving process
5 算例分析
5.1 仿真系统与参数设置
本文基于仿真环境i7-9750CPU,8G内存、MATLAB R2016b,以IEEE33 节点ADN 为算例进行分析,其网络结构如图5 所示,该系统包含33 条支路,辐射状运行,最大用户用电负荷有功为6 530 kW;最大用户用电负荷无功为5 222.7 kvar,用户负荷曲线如图6 所示。
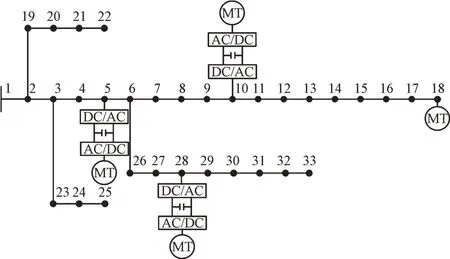
图5 主动配电网网络结构Fig.5 Active distribution network structure
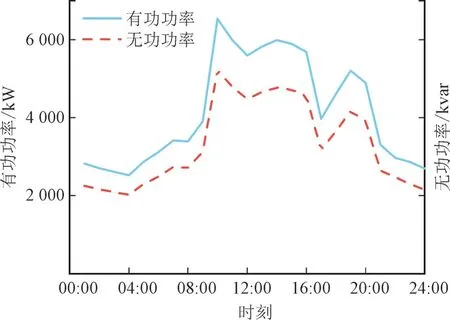
图6 用户负荷曲线Fig.6 Customer load curve
运行周期24 h;时段长度取1 h;节点18 连接1台WT,无功出力上限为400 kvar;节点5,10,28 各连接1 台MT,单位发电成本均为150 元/(MWh);VSC 损耗系数均为0.01,其参数如表1 所示。电压等级为12.66 kV;节点电压上下限分别为电压等级的1.05,0.95 倍;节点7,20,33 的负荷可削减,可削减上限均为200 kW,与上级电网交互有功功率上限100 kW,与上级电网交互无功上限为100 kvar;售电价格ω为0.45 元/kWh,与上级电网交互功率价格λP0为0.65 元/kWh;负荷削减价格λCUT为0.6 元/kWh。
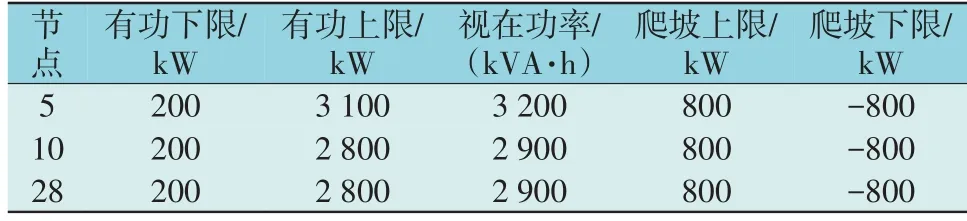
表1 MT模型参数Table 1 Parameters of MT model
UPFC 安装在节点8,9 之间,其参数如表2 所示。
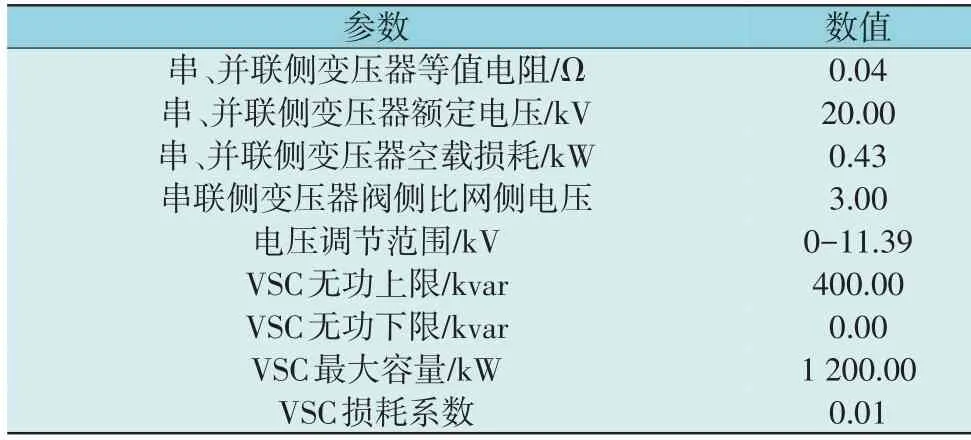
表2 UPFC模型参数Table 2 Parameters of UPFC model
根据历史数据采用神经网络算法预测WT 有功出力,其WT 各时段有功出力如图7 所示。
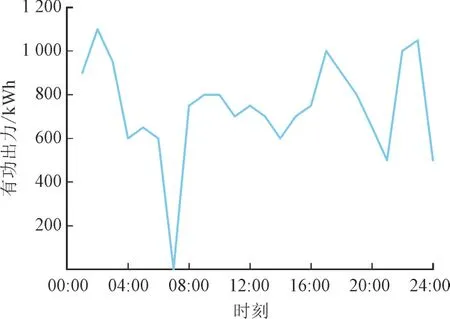
图7 WT预测出力Fig.7 Forecasted active power outputs of wind turbine
5.2 日前优化及实时优化
不计及UPFC 进行日前优化,与上级电网交互功率为0 kW,7 节点各时段负荷削减功率为0 kW,20,33 节点10 时的负荷削减分别为200,135.29 kW,最低优化运行成本为14 347.17 元。
基于日前WT 出力、用户负荷预测值进行优化运行,在引入UPFC 的基础上,各时段实时优化后,其最低的运行成本为14 340.63 元。较日前优化运行成本低6.54 元,其一部分为网络损耗节省,另一部分为网络损耗下降导致负荷削减量下降的节省。实时优化后各时段成本较日前优化后各时段成本变化曲线如图8 所示。

图8 调度成本变化曲线Fig.8 Operating cost curve
从图8 可知,1—9,12,14—24 h 成本略微下降,10—11,13 时成本下降明显。取调度时间10 h进行分析,其遗传算法收敛曲线如图9 所示。

图9 10 h实时优化收敛曲线Fig.9 Real time optimization convergence curve at 10:00
从图9 可知,在迭代50 次时已趋于收敛,优化值为1142.4 元,未计及UPFC 时网络损耗为79.39 kW;负荷削减共335 kW;MT 的VSC 损耗146.44 kW;实时优化后的网络损耗下降7.43 kW;MT 的VSC 损耗下降6.08 kW;UPFC 的损耗10.35 kW。总损耗下降,一定程度地改善了运行网络损耗,并利用节省网络损耗部分弥补了负荷不足,使得负荷削减下降3.16 kW。
5.3 算法对比分析
实时优化常采用模型预测控制(Model Predictive Control,MPC)理论进行滚动优化,为验证文中所提计及UPFC 的ADN 日前-实时优化策略的优越性,将其优化效果与基于智能算法的滚动优化进行比较,随机生成初值后,迭代4 000 次的情况下,10 h优化结果不能收敛,其值远大于文中策略优化值,因此,将文中日前优化的结果定为MPC 优化初值。为进一步验证所提算法有效性,在实时优化过程中考虑WT 出力和有功负荷的波动。WT 有功误差服从正态分布[23],即:
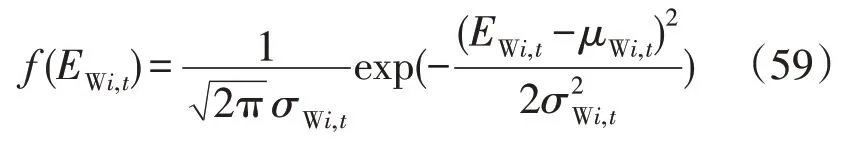
式中:EWi,t为t时刻节点i的WT 有功预测误差;σWi,t,μWi,t分别为其标准差和期望值。
令σWi,t为0.069,μWi,t为3.5 kW。WT 实际出力为:
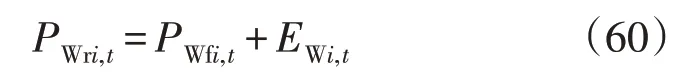
对于负荷,可认为其服从正态分布[24],即:
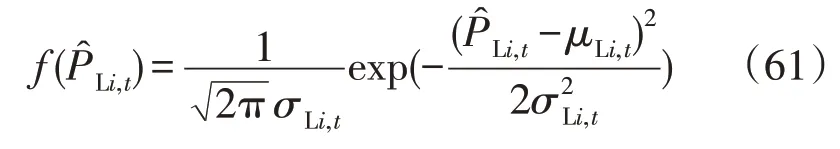
式中:σLi,t,μLi,t分别为t时刻节点i有功负荷的标准差和期望值。
令σLi,t为0.053,μLi,t为负荷预测值。假设负荷的无功功率为日前预测值。利用蒙特卡洛方法生成24 h 的WT 有功误差和负荷,重复上述过程形成4 个场景,另外,假设场景1 为负荷和WT 出力预测准确的情形。同样迭代50 次的情况下,5 个场景中两算法各时段优化运行时间大体一致,如图10 所示。成本差值如图11 所示。
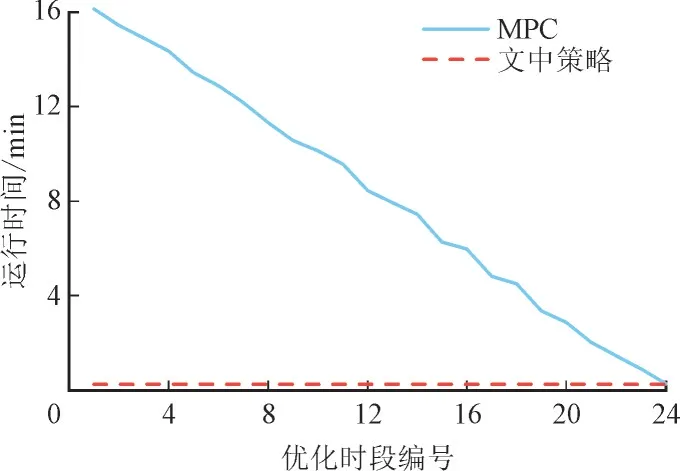
图10 各时段运行时间Fig.10 Running time of each period

图11 5个场景下2种算法调度成本差值Fig.11 Cost difference of two algorithms in five scenarios
由图10 可知,MPC 优化时间随着滚动小时数减少而减少;文中所提策略降低了求解维度,各时段优化时间明显低于MPC 优化时间。由图11 可知,5 个场景中,本文策略得到的各时段优化方案成本都低于MPC 得到的成本,提高了收敛性,解耦后的实时优化能更好地应对负荷和WT 出力波动。
6 结论
本文提出了计及UPFC 的ADN 日前-实时优化策略,通过对比MPC 与文中策略的优化结果,得出如下结论:
1)所提策略在实时优化阶段对MT 出力进行了时序解耦,能够在接入UPFC 的基础上,实现考虑电力系统运行全局最优的的单时段优化。
2)相较于滚动优化而言,所提策略降低了实时优化求解维度,具有更快的收敛速度,以提高实时优化的求解速度。
3)由于解耦后的实时优化求解维度降低,智能算法的搜索空间随之大幅度减少,使所提策略能更好地应对负荷和WT 出力波动,较MPC 方法具有更好的收敛特性。
此外,文中实时优化阶段仅对MT 进行了时序解耦,未来可进一步考虑储能等其它资源。

