基于正序分量相位差的电压暂降源定位方法

2022-07-26 04:18徐方维龙晨瑞陈家乐

智慧电力 2022年7期

徐方维，龙晨瑞，郭凯，贺东，陈家乐，周全，陈锴

（四川大学电气工程学院，四川成都 610065）

0 引言

电压暂降是电网中出现频次很高的电能质量扰动事件，产生的原因有短路故障、感应电机起动、变压器激磁等[1-2]。电压暂降会导致工业过程中断、工厂停产，造成巨大的经济损失[3-5]。随着高端制造业的发展以及新型电力系统“双高”态势下电力电子设备的涌现，电压暂降敏感设备并网数量日益增多，用户对电网电能质量的要求与重视程度也随之不断提升。电压暂降扰动源可出现在输电系统、配电系统以及工业用户作业区内。由于电压暂降不可避免，因此准确定位电压暂降扰动源可为电压暂降治理和管控提供决策依据，有利于优化电力营商环境和提高用户“获得电力”指数。

电压暂降源定位指确定引起电压暂降的扰动源与监测装置相对位置的方法，一般从能量流动[6-9]和电网参数变化[10-11]2 个方面进行研究。在能量流动方面：文献[6] 最早提出利用扰动功率法（Disturbance Power and Energy，DPE）进行定位，但仅适用于单端供电的情况，在多电源网络中无法应用。文献[7-9]通过算法优化和改进扰动功率的提取方式提高了DPE 在多扰动源类型场景下的精度，但在环网和多回路网络中，扰动源引起的复杂功率变化将导致这些方法失效。在电网参数变化方面：文献[10]利用电流实部极性进行定位，所需参数易于获取且计算过程简便，但存在三相判断不一致的缺陷。文献[11]通过拟合电流、电压和功率因数，利用拟合曲线斜率进行定位，所提取的大量特征参数提高了定位准确度，但仅适用于对称故障。目前用于电网故障定位的方法为暂降源定位拓展了新的研究思路：文献[12-14]考虑优化监测装置布点来定位暂降源，定位结果准确性高，缺点是对电网可观性要求过高、参数获取难度较大。文献[15-19]基于综合判据和智能算法可精确定位故障点度，缺点是计算流程复杂、工程实现度差。

综上所述，提高复杂网架结构和多扰动源类型场景下电压暂降源定位结果的准确率，具有较大的经济价值。因此，本文提出一种基于正序分量相位差的电压暂降源定位方法，以暂降期间电压与电流间相位差作为判据，表征监测点与扰动源相对位置不同时扰动源引起的功率转移规律，避免了复杂网架结构下直接通过功率定位暂降源的缺陷。研究的创新之处在于引入瞬时对称分量法，使判据适用于各类扰动源。

1 电压暂降源定位原理

1.1 扰动源作用下电网功率传输特性

电力系统中，电压暂降多由短路故障等扰动引起。由于电网中出现多重故障的概率较低[20]，因此本文仅考虑单次扰动引起电压暂降的情况。以短路故障扰动为例，短路故障前后电网等值电路如图1 所示。

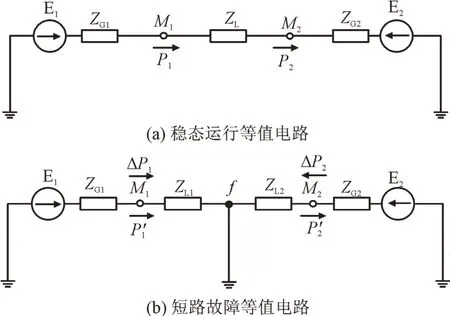
图1 短路故障前后电网等值电路Fig.1 Grid equivalent circuit before and after short circuit

图1 中，E1，E2分别为等效电源，M1—M2为监测点，f为故障点，ZG1，ZG2分别为电源内阻抗，ZL为稳态运行时M1与M2之间的线路阻抗，ZL1为短路故障时M1与f之间的线路阻抗，ZL2为短路故障时M2与f之间的线路阻抗，P1，P2分别为稳态运行时M1和M2处有功功率，分别为短路故障时M1和M2处有功功率，ΔP1，ΔP2分别为短路故障时M1和M2处有功功率变化量。

扰动功率[6]（Disturbance Power，DP）为扰动期间有功功率与扰动发生前有功功率之差，扰动能量（Disturbance Energy，DE）为扰动期间DP 对时间的积分。图1 中f点发生短路故障时，监测点M1处的DP 和DE 分别为：

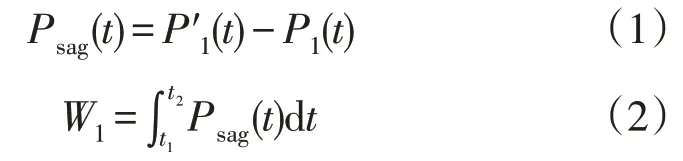
式中：Psag（t），W1分别为短路故障时M1处的DP 与DE；分别为短路故障前后监测点M1处的瞬时功率；t1，t2分别为扰动起、止时间。

由于故障点f在监测点M1的下游，可知W1为正值[6]，则扰动发生前后M1处有功功率关系为：

扰动期间，图1（b）中ΔP1与图1（a）中P1同向传输导致大于P1；同理，ΔP2与P2反向传输导致P′2小于P2。采用线性电路的叠加原理分析上述过程，可知f点短路故障时故障点在电势源作用下的等值电路如图2 所示。

图2 故障点在电势源作用下的等值电路Fig.2 Equivalent circuit of fault point under potential action

图2 中，Ef为故障点f电势源，Vf为Ef的电势，If为短路电流。图2（a）为仅在Ef激励下的扰动源等值电路，图2（b）为Ef，E1，E2共同激励下的短路故障等值电路。由图2（b）可知，If与Vf方向相反，表明故障点f的电势源向电网吸收功率，将部分有功功率向故障点传输。

1.2 电压暂降源定位依据

电力系统中出现暂态扰动事件时可将扰动源看作能量汇聚点。如短路故障期间能量从系统中其他负荷转移至故障线路[6]，大型感应电机起动时从系统汲取大量有功功率。监测点与扰动源相对位置不同时，扰动源引起的功率转移对监测点处有功潮流的影响存在差异。

1.2.1 汇集能量

电网稳态运行时，输电线路和系统各节点的功率分布基本保持不变。扰动出现导致电压暂降时，线路传输功率的大小、方向会发生改变，引起电网中部分有功功率向扰动源汇聚。本文将这部分功率视为“汇集能量”，定义为在电压暂降扰动源作用下从系统其他负荷或电源向扰动源传输的有功功率，用PCON表示。图1（b）中的ΔP1和ΔP2即为故障点电势源作用下系统向故障点转移的PCON。

根据监测点采集的数据确定PCON的流向，可判断扰动源的相对位置。如图1 所示，通过监测点M1采集的数据得出PCON向下游传输，可知扰动源位于M1的下游。但是采用判断扰动期间功率传输方向来定位扰动源的方法[6-9]，其定位判据反映的是电网实际潮流方向而非PCON的传输方向，若网络中存在2 个及以上电源时会出现定位判据失效的情况。为规避网架结构和电源对定位结果的影响，不应直接使用监测点有功功率作为判据。

1.2.2 功率传输

交流电网并联系统中各单元输出电压的相位变化会造成有功功率的差异，且有功功率总是从电压相位超前的一端传输至电压相位滞后的一端。因为输送有功功率会引起相位差，所以PCON的传输会对稳态电压相位产生影响。当系统稳态运行时，输电线路两端电压相角差的余弦值为：

式中：δ为任意输电线路两端电压之间的相角差。

由式（4）可知，电力系统稳态运行时输电线路两端电压相位差较小，可推断引起相位改变的因素来自系统受到的扰动。

1.3 定位原理分析

PCON的传输会引起电压电流相位变化：当PCON与原有功功率潮流方向一致时，电压相位超前程度减弱，电流相位滞后程度减弱；当PCON与原有功功率潮流方向不一致时，电压相位超前程度增强，电流相位滞后程度增强[21]。以图1（b）中监测点M1，M2处电压电流相位变化与其所对应的汇集能量PCON1，PCON2传输方向的关系为例，扰动源与监测点相对位置不同时电压电流的相位变化如图3 所示。

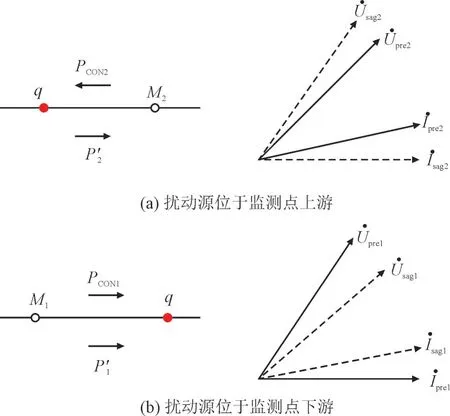
图3 扰动源与监测点相对位置不同时电压电流的相位变化Fig.3 Phase changes of voltage and current at different relative positions of disturbance source and meter

不对称故障引起的电压暂降中非故障相的电压、电流相位变化较小，只能通过故障相的电压与电流相位差定位扰动源，因此需先判断出故障相。为免去判断故障相这一步骤，引入瞬时对称分量法[22]以提高定位效率。电压暂降期间的基频相电压与基频相电流分别为：

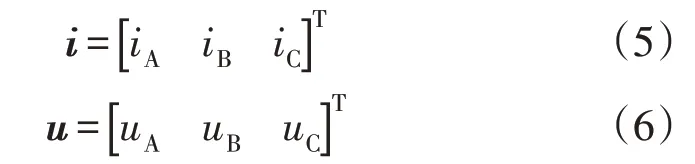
式中：i，u分别为基频相电流矢量与基频相电压矢量；iA，iB，iC分别为A 相、B 相和C 相的相电流；uA，uB，uC分别为A 相、B 相和C 相的相电压。

基频相电压与基频相电流的各序分量表达式为：

式中：ics，ucs分别为电流基准相和电压基准相的各序分量；a，F 为算子；e 为自然底数，j 为虚部；i1，i2，i0分别为相电流正序、负序和零序分量；u1，u2，u0分别为相电压正序、负序和零序分量。

ics，ucs的实数形式分别为：

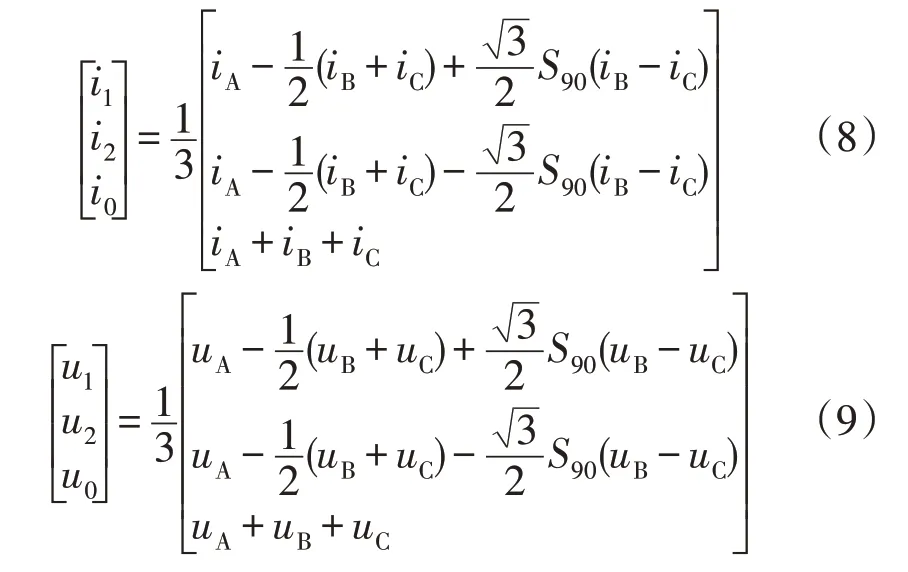
式中：S90为移相算子。

瞬时对称分量法引入后，可使用u和i各序分量的相位差定位扰动源，无需判断故障相。考虑到电流零序分量无法流通星形连接和三角形连接绕组变压器，且扰动源为三相短路、变压器激磁和大电机起动时电网中电压与电流不存在负序分量，故选用相电压正序分量和相电流正序分量的相位差（简称正序分量相位差）作为判据，其表达式为：

式中：θ+为正序分量相位差；∠u1为相电压正序分量的相角；∠i1为相电流正序分量的相角。

2 电压暂降源定位判据分析

以一次变压器激磁引起的电压暂降为例，扰动源与监测点相对位置不同时，监测点处正序分量相位差曲线如图4 所示。此次电压暂降的起、止时间分别为第0.04 s 和第0.06 s。

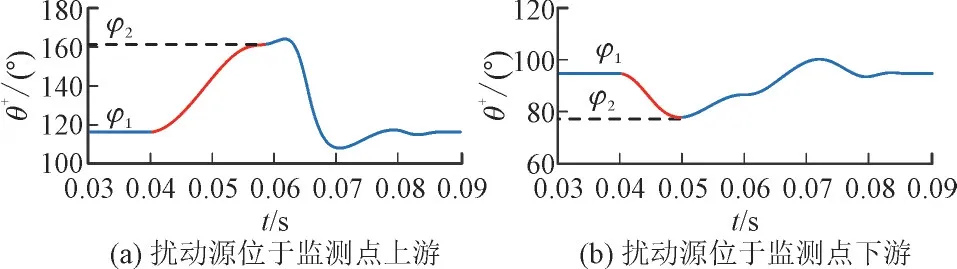
图4 监测点处正序分量相位差曲线Fig.4 Phase difference curves of positive sequence components at meters

图4 中，φ1为暂降发生前θ+的稳态值，φ2为扰动期间θ+的初始峰值。根据扰动源相对位置与PCON传输方向的关系，结合功率传输对θ+变化趋势的影响，得到利用θ+进行电压暂降源定位的判据。具体表现为2 种形式：

1）扰动出现后，若θ+曲线的斜率为正，即θ+逐渐增大（图4 中用红色标注的部分），则扰动源在测点上游；若θ+曲线的斜率为负，即θ+逐渐减小，则扰动源在测点下游。以θ+曲线斜率作为特征量的判据表达式为：

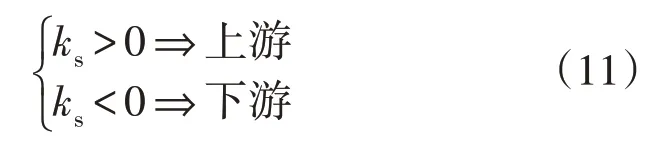
式中：ks为扰动出现后θ+曲线斜率。

2）若θ+曲线的第1 个波峰极性为负，则扰动源在监测点下游且极性为正，判断扰动源在监测点上游。以θ+曲线波峰极性为特征量的判据表达式为：

由于PCON的传输方向和大小仅与扰动源所在位置及电网元件的阻抗有关，与电源和实际潮流方向无关，因此判据式（11）－式（12）不受网架结构限制。在图1 中f点处设置各类扰动源，电压暂降的起、止时间分别为第0.04 s 和第0.06 s，监测点M1与M2处不同扰动源类型下正序分量相位差曲线如图5 所示。

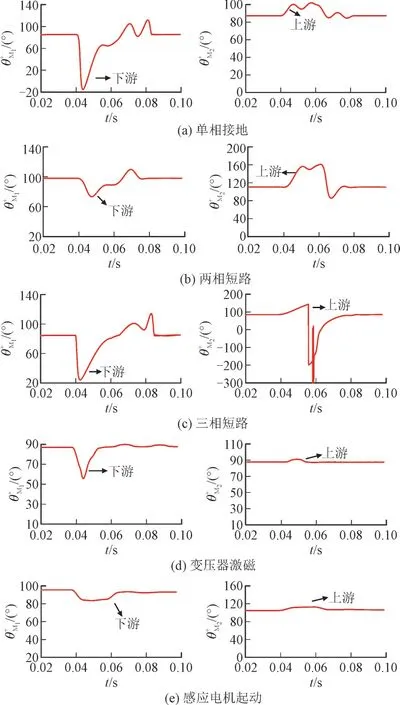
图5 不同扰动源类型下正序分量相位差曲线Fig.5 Phase difference curves of positive sequence components under various disturbance source types

电力系统中变压器绕组最常用的连接方式为Yy0（星形连接/星形连接-12 点钟）和Yd11（星形连接/三角形连接-11 点钟），当阻隔在监测点与扰动源之间的变压器绕组为这2 种连接方式时，判据式（11）－式（12）仍然适用。因为电压与电流的各序分量经过Yy0 连接的变压器时不会发生相位移动，而正序电压与正序电流经过一切奇数点钟Yd（星形连接/三角形连接）连接的变压器时低压侧均会超前高压侧30°，所以即使扰动源与监测点之间有变压器阻隔，θ+的变化规律也不会改变。同时，应用式（11）－式（12）可避免对整个电压暂降持续期间内的功率变化进行分析，不仅大大简化了计算过程，而且使判据在复杂网架结构、多电源供电网络中仍然保持了较高准确性。

综上所述，本文所提方法进行电压暂降源定位的步骤为：（1）提取单次电压暂降事件所记录的三相基频电压瞬时值、电流瞬时值，经瞬时对称分量法得到对应的正序分量；（2）绘制相电压与相电流基频正序分量相位差随时间变化的曲线，根据式（11）－式（12）判断出电压暂降事件扰动源与监测装置的相对位置。

3 仿真与实例验证

为验证复杂网架结构和多扰动源场景下本文方法的有效性与准确性，在辐射型网络、环形网络和多回路网络中设置不同类型扰动源进行仿真分析。由于传统定位方法[6-11]不适用于环形网络和多回路网络，因此在这2 种网络下仅就本文方法进行分析。

3.1 辐射型网络

单回路辐射型网络如图6 所示。

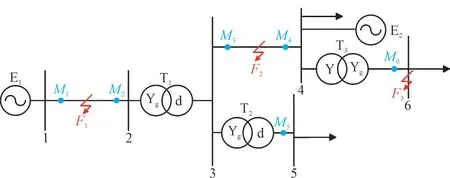
图6 单回路辐射型网络Fig.6 Single loop radiant network

图6 中，1—6 为母线，M1－M6为监测点，F1－F3为扰动源位置，变压器T1的变压比为110/10 kV，变压器T2和T3的变压比均为10.5/0.4 kV，“Y”表示变压器绕组为星形连接，“Yg”表示变压器绕组星形连接且中性点接地，“d”表示变压器绕组为三角形连接，母线4—母线6 所带负荷分别为（60+j4.8）MVA，（470+j40）kVA 和（800+j50）kVA。扰动源类型设置为对称故障（三相短路）、不对称故障（单相接地、两相接地和两相短路）、感应电机起动及变压器激磁。其中变压器激磁设置为三相变压器带负载通电，F1，F2处变压比分别设置为110/10 kV 和10/0.4 kV，母线6 电压等级为0.4 kV，由于工况中此电压等级不会出现变压器投切的情况，故F3处不再设置变压器激磁。电网中大型感应电机起动引起电压暂降的情况通常发生在10 kV 或6 kV 工业用户侧，因此只在母线3和母线4 设置感应电机起动，并将感应电机起动设置为母线带额定功率为165 kW 的三相鼠笼异步电机直接起动。若监测点所在母线的电压未跌落至0.9 p.u.以下，则判定此次扰动未引起该母线电压暂降，在仿真结果中不记录该监测点的判断结果。

在辐射型网络中，选取3 种在智能算法和工程中使用较广泛的传统定位方法与本文所提方法进行对比，其中方法1 为本文所提方法，方法2 为扰动功率法[6]，方法3 为系统轨迹斜率法[11]（Slope of System Trajectory，SST），方法4 为实部电流极性法[10]（Real Current Component，RCC）。调整扰动源位置，分别对每种方法进行92 次仿真验证，其中对称故障17 次，不对称故障51 次，变压器激磁12 次，感应电机起动12 次。不同监测点处4 种电压暂降源定位方法的判断结果如表1 所示，判断结果中“↑”表示扰动源在上游，“↓”表示扰动源在下游，黑色箭头表示判断正确，红色箭头表示判断错误，“*”表示此次扰动未造成电压暂降，“-”表示此种方法在此种条件下无法使用。例如F1处两相接地故障时，监测点M2的判断结果为“”，表示方法1判断结果为上游且判断正确，方法2 判断结果为下游但判断错误，方法3 无法使用，方法4 判断结果为上游但判断错误。

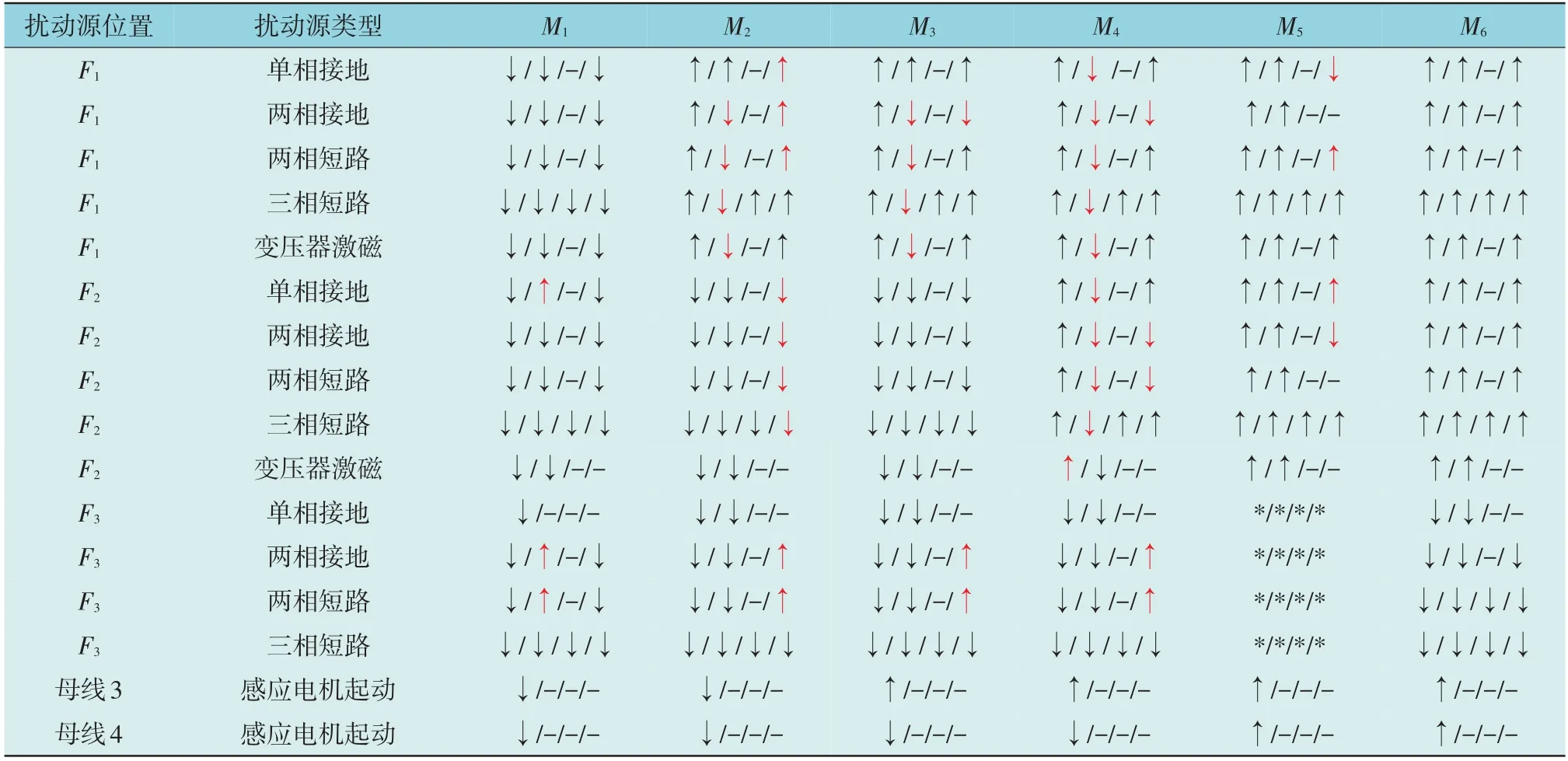
表1 不同监测点处4种电压暂降源定位方法的判断结果Table 1 Judgment results of four voltage sag source location methods at different meters

由表1 可知，在单相接地、两相接地、两相短路、三相短路、变压器激磁和感应电机起动6 种扰动源类型下，方法1 判断正确次数分别为17，51，11 和12；方法2 判断正确次数分别为13，14，8 和0；方法3 判断正确次数分别为17，0，0 和0；方法4判断正确次数分别为17，31，6 和0。综上，方法1准确率分别为100%，100%，91.67%和100%；方法2准确率分别为76.47%，72.55%，66.67%和0；方法3准确率分别为100%，0，0 和0；方法4 准确率分别为100%，60.78%，50%和0。

为分析相位跳变对4 种定位方法的影响，在图6中F2处设置三相短路故障，调整F2在线路中的位置以改变故障点至母线3 的馈线阻抗，分析不同程度相位跳变下4 种方法在监测点M3与M4的准确率。根据工程中相位跳变最极端的情况，设置相位跳变值Δφ的变化区间为（-60°，+20°）。考虑实际工况[23]，对系统阻抗ZS做如下设置：110 kV 线路阻抗为（19+j7.16）Ω，变压器T1阻抗为（3.658+j79.322）Ω，即ZS为（22.658+j86.482）Ω。不同Δφ取值条件下4 种方法在各监测点的判断结果如表2 所示。

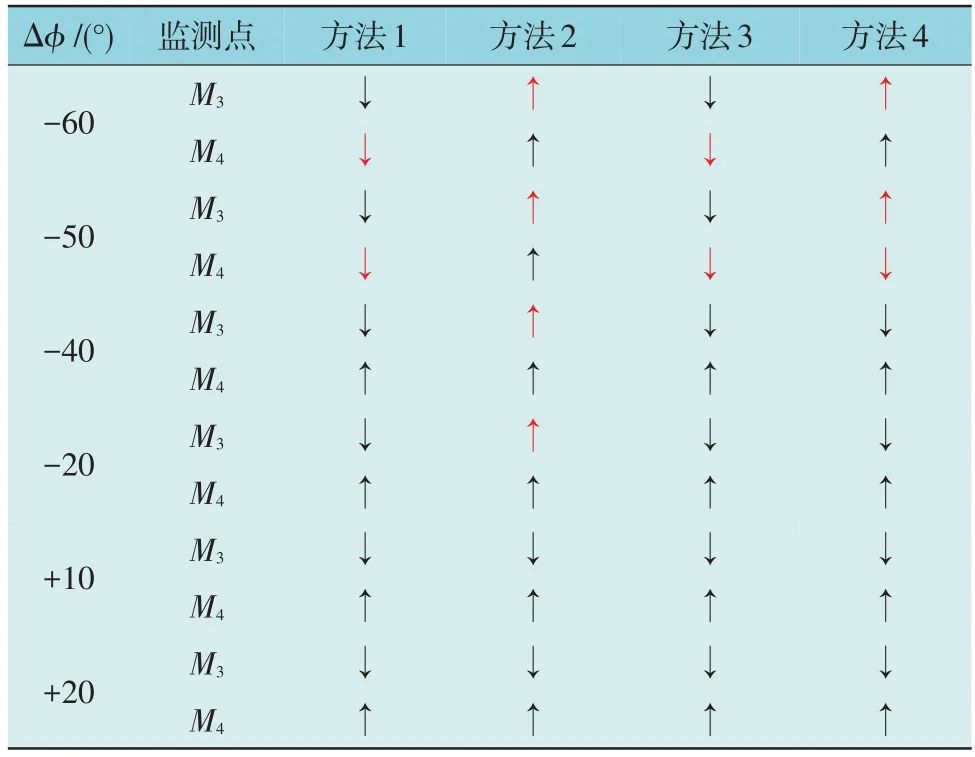
表2 不同Δφ 取值条件下4种方法在各监测点的判断结果Table 2 Judgment results of 4 methods with different Δφ at different meters

鉴于配电电缆故障及输电系统故障引起的相位跳变大多分布于(-20°,+20°)区间[24]，可认为相位跳变对上述4 种方法的影响较小。

3.2 环形网络

IEEE 9 节电网如图7 所示，参数设置见文献[25]，初始有功功率方向如黑色箭头所示。

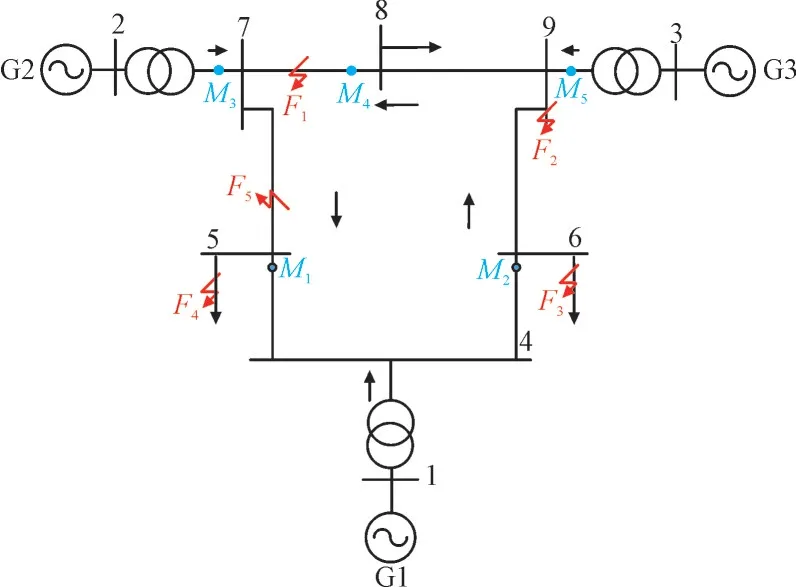
图7 IEEE9节点电网Fig.7 IEEE 9 nodes network

图7 中，G1－G3 为发电机，F1－F5为扰动源位置，M1－M5为监测点，1—9 为母线。在F1－F5处均设置单相接地、两相接地、两相短路和三相短路故障，环形网络短路故障情况下各监测点的判断结果如表3 所示。表3 中，如在F1设置4 种短路故障时，监测点M1的判断结果为“↓/↑/↑/↑”，表示本文方法在单相接地情况下判断结果为下游但判断错误，两相接地、两相短路和三相短路故障情况下判断结果均为上游且判断正确。

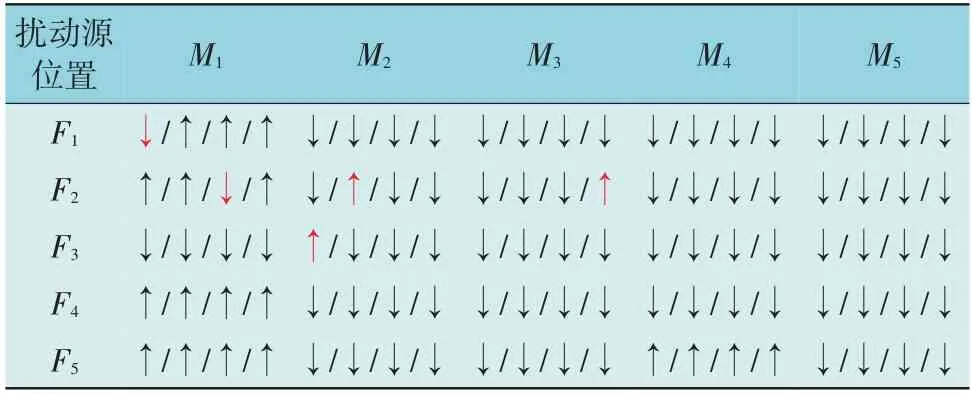
表3 环形网络短路故障情况下各监测点的判断结果Table 3 Judgment results of each meter under shortcircuit fault in loop network

在母线5 与母线6 处分别设置感应电机起动，环形网络中非短路故障时各监测点的判断结果如表4 所示。

表4 环形网络中非短路故障时各监测点的判断结果Table 4 Judgment results of each meter under nonshort circuit fault in loop network

由表3 和表4 可知，100 次短路故障仿真中本文方法判断正确95 次，10 次感应电机起动仿真中本文方法全部判断正确。本文方法在环形网络中定位准确率为95.45%。

3.3 多回路网络

IEEE14 节点电网如图8 所示。图8 中，G1－G2为同步发电机，C 为同步调相机，1—14 为母线，F1－F4为扰动源位置，M1－M4为监测点。

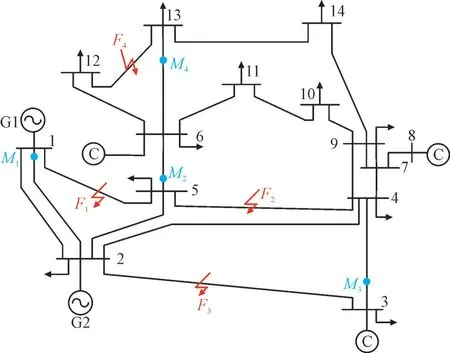
图8 IEEE14节点电网Fig.8 IEEE 14 nodes standard network

在F1－F4均设置单相接地、两相接地、两相短路和三相短路故障，多回路网络中短路故障情况下各监测点的判断结果如表5 所示。

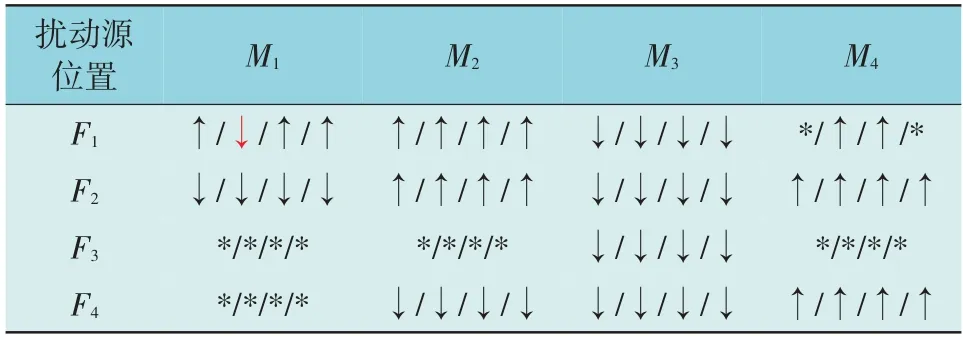
表5 多回路网络中短路故障情况下各监测点的判断结果Table 5 Judgment results of each meter under the condition of short-circuit fault in multi-loop network

在图8 中母线3—母线5 处分别设置感应电机起动和变压器激磁，多回路网络中非短路故障时各监测点的判断结果如表6 所示。

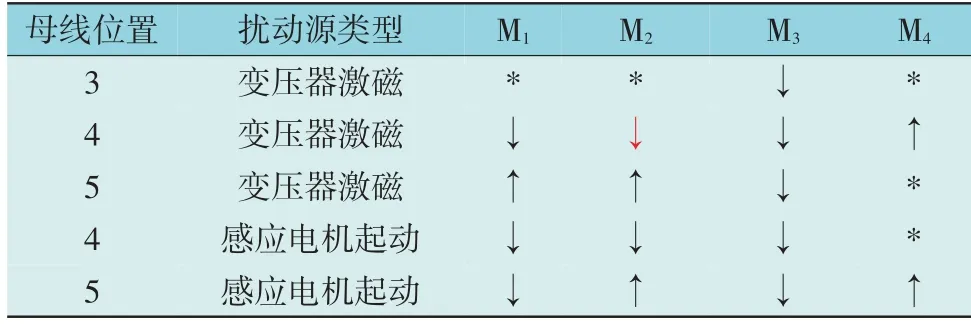
表6 多回路网络中非短路故障时各监测点的判断结果Table 6 Judgment results of each meter under nonshort circuit fault in multi-loop network

由表5 和表6 可知，46 次短路故障仿真中本文方法判断正确45 次，8 次变压器激磁仿真中本文方法判断正确7 次，7 次感应电机起动仿真中本文方法全部判断正确。本文方法在多回路网络中准确率为96.72%。

3.4 仿真结果分析

根据表1—表6 中判断结果，得到不同仿真场景中定位方法准确率如图9 所示。

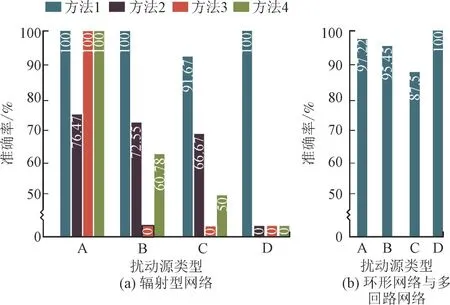
图9 不同仿真场景中定位方法准确率Fig.9 Accuracy of location method under different simulation cases

图9 中，扰动源类型A，B，C，D 分别表示对称故障、不对称故障、变压器激磁和感应电机起动。由图9 可知，在对称故障、不对称故障和感应电机起动3 种仿真场景中方法1 均有较高的准确率，尤其在辐射型网络中，方法1 的表现更是优于其它3种方法。仿真结果表明，本文所提方法不受网架结构和扰动源类型的限制，在不同条件下均可以准确判断出电压暂降扰动源的相对位置。

3.5 实例数据验证

实例数据来自东南沿海某市配电网发生的一次电压暂降事件中3 个站点（110 kV CQ 站、110 kV HY 站和220 kV CX 站）电能质量监测装置记录的三相电压与三相电流瞬时值。实例数据得到的正序分量相位差曲线如图10 所示。

图10 实例数据得到的正序分量相位差曲线Fig.10 Phase difference curve of positive sequence in field case

图10 中红色虚线框内曲线为暂降发生后θ+的变化趋势，由式（10）－式（11）可知扰动源位于CQ 站与HY 站的上游、CX 站的下游，判断结果与实际相符。

4 结语

本文以电网出现电压暂降扰动源时功率流动的特性为基础，提出一种利用正序分量相位差进行电压暂降源定位的方法。在辐射型网络中多种扰动源类型情况下，与扰动功率法、系统轨迹斜率法和实部电流极性法相比，本文所提方法准确性更高，适用性更广。

仿真结果表明，当网架结构为辐射型网络、环形网络和多回路网络，扰动源为对称故障、非对称故障、变压器激磁和感应电机起动时，所提方法均可判断电压暂降扰动源相对位置。利用本文方法可高效辨识扰动源所在区域，准确筛选扰动源所在线路，如果需要进一步对扰动源进行精确定位，还可在此基础上结合故障点匹配和行波测距等方法来实现。