基于指数变换的对流占优反应扩散问题的有限体积法

邹享明

（东北大学理学院，辽宁 沈阳 110000）

引言：考虑对流占优反应扩散方程：

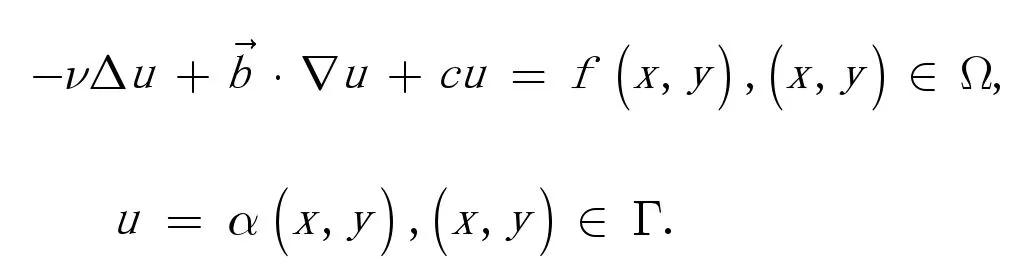
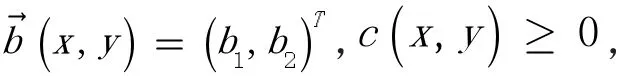
Peclet 数

时，方程呈现双曲性质，称为对流占优反应扩散方程。方程的解在靠近求解区域的部分边界附近急速变化，称为边界层现象，且Peclet 数越大，边界层区域越窄。

1 问题守恒形式和差分格式的构造

将方程转化为主部守恒形式，ρ (x,y),同时利用Green公式，得：

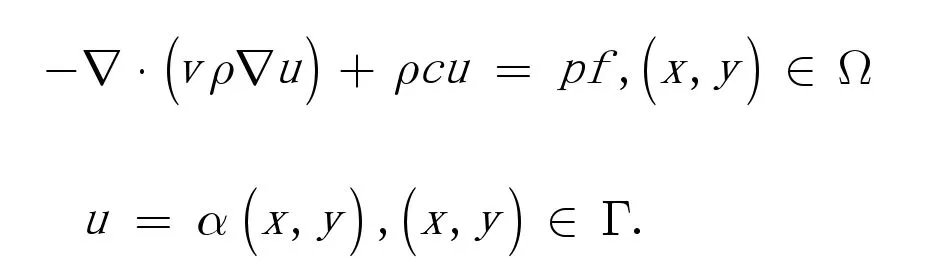
本文从该方程出发构建相应的有限体积元格式。

考虑如图1 所示单元。对原方程在V0上积分，利用格林公式，有

图1 外心对偶剖分网格

对式中V0上的积分有

其中S0是V0的面积；

对边界上的积分有

得到方程解在有限体积单元V0上的离散格式：

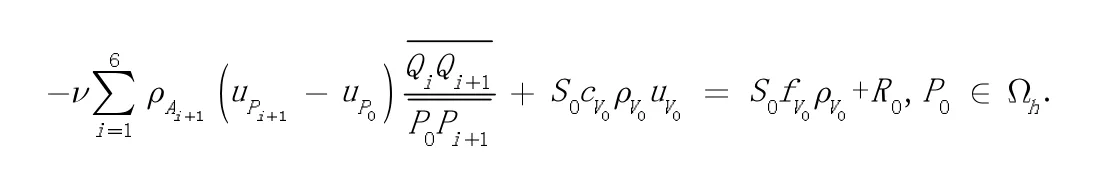
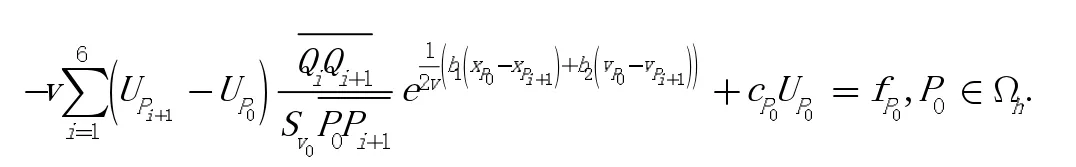
下面讨论差分方程的性质。在不引起混淆的情况下简化下标，可改写为：的相邻节点集为M0，定义正则节点集，非正则节点集：

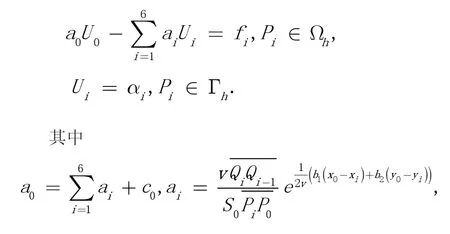
当Pi是非正则内点时，由边界条件得

定义差分算子：

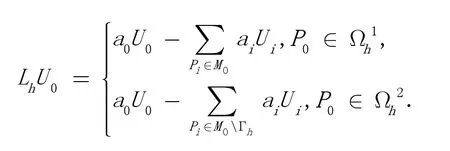
则差分方程可改写为：

其中

易知Lh满足：

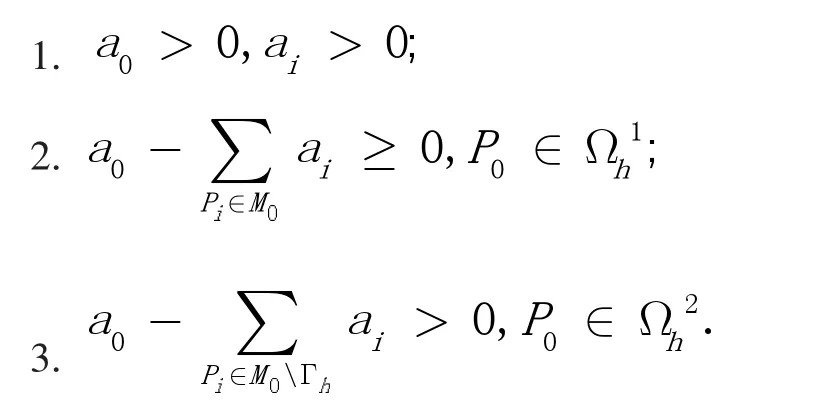
因此Lh是椭圆型差分算子，方程解的存在唯一性由文献[1]给出。

2 解的稳定性分析

考虑一种网格边长为h 的正三角形剖分。不妨设P0

设Pi∊Ω是一个内节点，当Pi的所有相邻节点均为内节点时，称为正则节点，否则称为非正则节点。记Pi

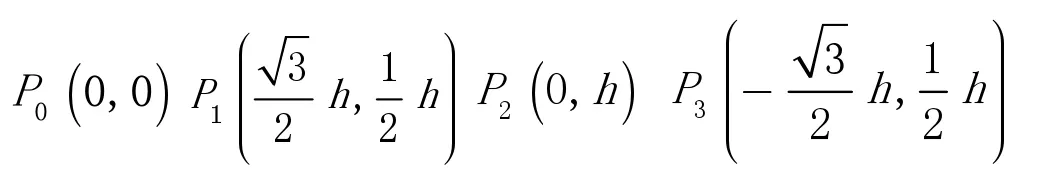
首先证明W0在 Ωh2上取得其在 Ωh上的正的最大值。

若W0在 Ωh上为常数，结论成立；设W0不是常数，假设W0在上取得正的最大值M，必存在P0∊使得 W0=M ，同时存在 Pi∊ M0使得 Wi＜M。又ai> 0，有

矛盾，所以W0在上取得其在 Ωh上的正的最大值。

引理2 得证。

定理1：差分方程

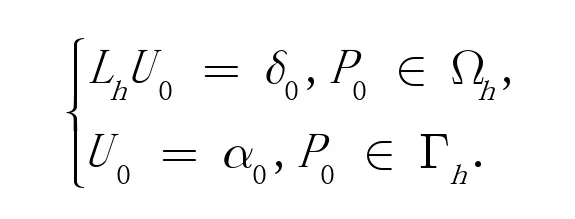
其中

证明：解的存在唯一性由定理1 给出。下面进行最大模稳定性估计：

将解分解为

则

定理2 得证。

3 解的误差分析

由引理1 得

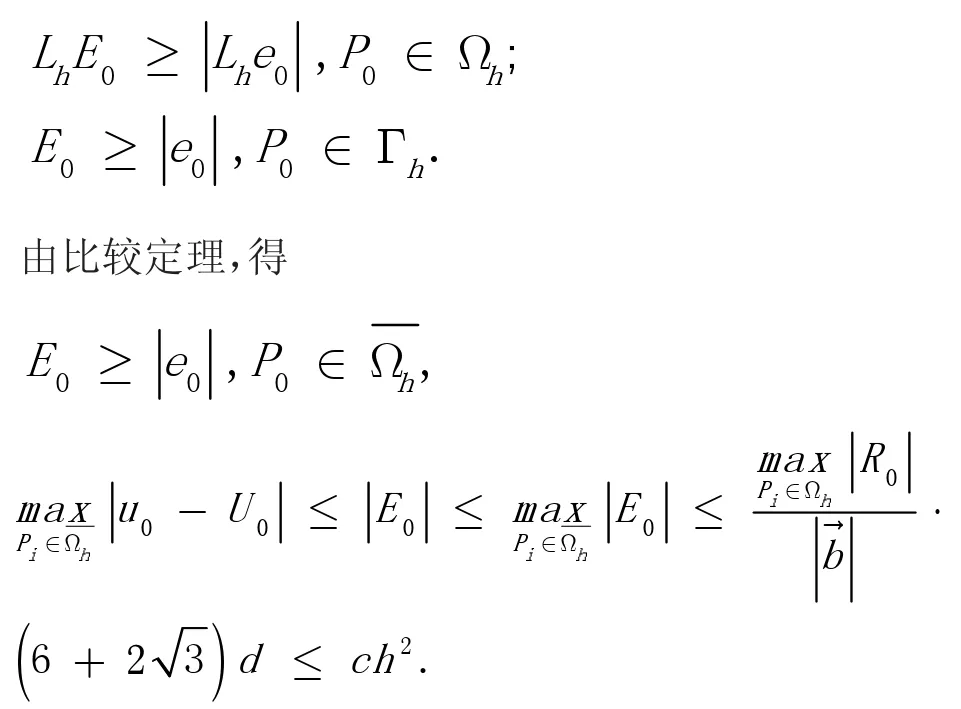
定理3 得证。

最后讨论对流项系数不是常数的情形。引进对流项系数及相应指数变换在有限体积剖分区域上的分片常数逼近,

则方程在控制体积上改写为：

在有限体积单元上积分，并利用格林公式，得

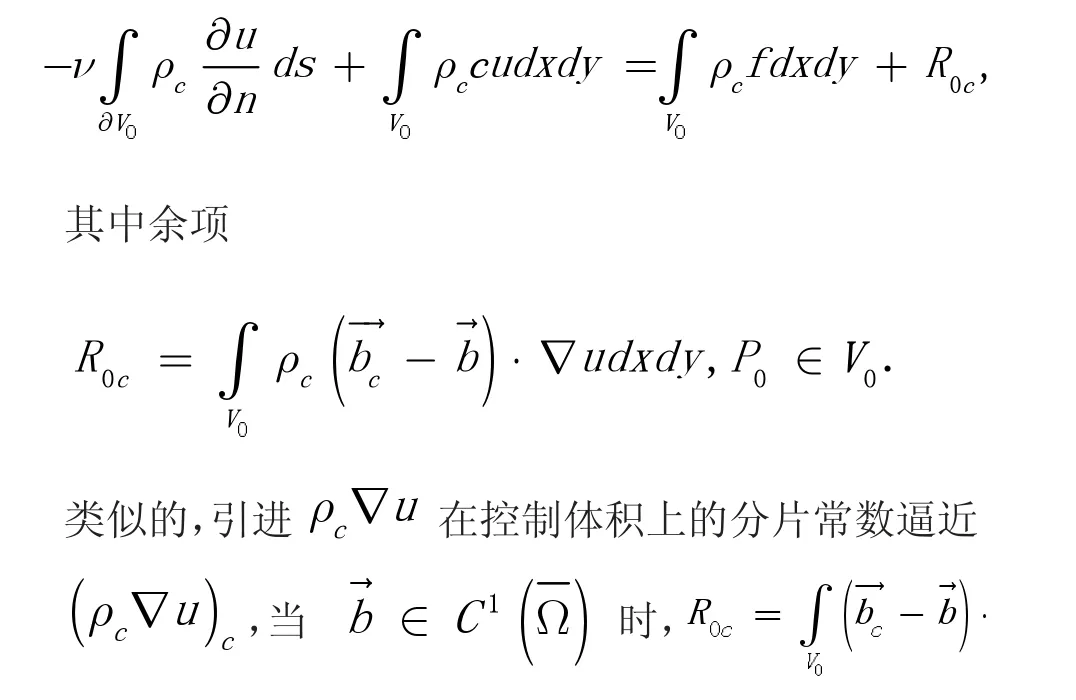
类似的，则可得到与之前差分方程一致的守恒型差分格式，其中用-→代替，且截断误差保持为 0 ( h2)。