大模数齿轮齿条机构建模与静力学分析*

盛洪潇

(三峡大学 机械与动力学院，湖北 宜昌 443002)

0 引 言

作为大国重器的典型代表，三峡升船机和龙源振华叁号都是大模数齿轮齿条驱动式起升工作平台[1]。大模数齿轮齿条起升机构作为其关键零部件具有传动效率高、传动精度高、结构紧凑、使用寿命长等优点。诸多优点使得齿轮齿条机构广泛应用于大型机械上,如矿山机械、石油机械、升船机械、海洋平台等大型升降设备。

王振[2]将三峡升船机中的大模数齿轮齿条机构作为分析对象，使用理论计算与有限元分析结合的方法，推断出改变修正系数选取方法后的国标计算公式。

唐文献等[3]针对风电安装船齿轮齿条式升降系统，建立了超大模数齿轮齿条有限元分析模型，研究了齿轮的变位系数、压力角、模数等参数对齿轮齿条弯曲强度及接触强度的影响。

为了研究齿轮齿条机构的接触应力，张兴权等[4]运用齿轮承载能力计算方法中的接触应力计算公式，求解了齿轮齿条机构在不同位置啮合时的接触应力。

笔者主要对不同工况参数条件下的齿轮齿条传动系统展开研究，结合理论公式计算与计算机软件分析，建立齿轮齿条机构的三维实体模型，研究在对应工况下齿轮弯曲应力和接触应力的大小、分布规律。

1 齿轮齿条材料参数与设计参数

齿轮传动机构工况复杂，并且在机械设备的工作中发挥十分重要的作用，为了保证设备的安全运行，需要对不同工况条件下的齿轮强度进行校核，一般要计算齿轮的齿根弯曲应力和齿面接触应力，对比这两个应力是否在材料的安全范围之内，以此来验证齿轮的强度是否满足要求[1]。

本文所分析研究的齿轮齿条材料参数及设计参数如表1所列。

表1 齿轮齿条的材料及设计参数

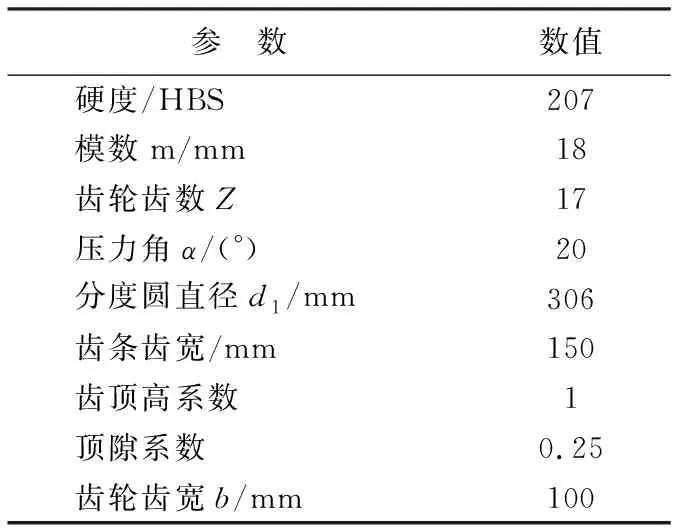
续表1 齿轮齿条的材料及设计参数

参考齿轮齿条升降装置的实际工况，设置6组不同工况条件下的齿轮切向力Ft，依据式(1)，计算出齿轮运行时所受力矩t0的大小，为了便于计算和分析，将使用输入力矩t1来进行理论计算和有限元分析。6组工况参数如表2所列。

表2 齿轮齿条的工况参数

t0=Ftd1/2

(1)

式中：t0为齿轮工作时受到的力矩；Ft为齿轮切向力；d1为齿轮分度圆直径。

2 理论计算

齿轮齿条强度的理论计算部分主要包括弯曲应力计算和接触应力计算[5]，本文中采用ISO公式[6]来计算齿轮弯曲应力，采用30°切线法确定齿根弯曲应力的危险截面[7]，齿轮的齿根弯曲应力计算公式：

(2)

式中：KF为弯曲强度计算的载荷系数；Ft1为齿轮圆周力；YFa为载荷作用于单对齿啮合区上届点时的齿形系数，与齿制、变位系数和齿数有关，与模数无关；Ysa为载荷作用于单对齿啮合区上界点时的的应力修正系数；Yε为齿轮弯曲强度计算的重合度系数；b为齿轮齿宽；m为齿轮模数。

将六种工况的参数带入式(2)可得齿根弯曲应力如表3所列，这些值作为齿轮弯曲应力的理论计算结果，将与后续的有限元分析结果做比较。

表3 齿轮弯曲应力的理论计算值

齿轮接触应力采用Hertz理论的计算公式，为了使计算结果更加符合实际，学者们引入更多参数对公式进行了修正[8]，最终得到了现在的齿轮齿面接触应力计算公式(3)：

(3)

式中：σH为齿轮的齿面接触应力；ZH为节点区域系数；ZE为齿轮材料的弹性影响系数；Zε为齿轮重合度系数；Zβ为齿轮螺旋角系数；b为齿轮齿宽；υ为齿轮传动比，齿轮齿条传动;υ取无穷大；KH为齿轮接触强度计算的载荷系数。

将六种工况参数带入式(3)可得齿面接触应力如表4所列，这些值和表3中的值作为齿轮齿根弯曲应力和齿面接触应力的理论计算结果，将与后续有限元分析结果作对比。

表4 齿轮接触应力理论计算值

3 建模与静力学分析

有限元法核心思想是把连续的结构分散成有限多个离散的单元，对每个单元分别进行计算后再组合到一起就能得到整体的力学特性，将复杂的实际问题大为简化并得出比较精确的分析结果。文中采用SolidWorks软件来建立齿轮齿条实体模型，再利用软件相关联的端口将模型导入ANSYS软件展开分析。所建立的齿轮齿条啮合模型如图1所示。

图1 齿轮齿条啮合模型

接下来就是建立有限元分析模型，施加约束条件和载荷等。为了提高分析精确度，需要对接触区域的网格进行加密，使用级别3加密后得到的总划分节点41449个，总划分单元24835。处理完之后的齿轮齿条模型如图2所示。如图3所示，静力学分析齿轮的齿根弯曲应力和齿面接触应力需要将齿轮齿条固定，为了方便给齿轮输入力矩，在静态结构中给齿条施加固定支撑，给齿轮施加圆柱形支撑，根据表2的工况参数输入力矩的大小和方向然后进行求解。

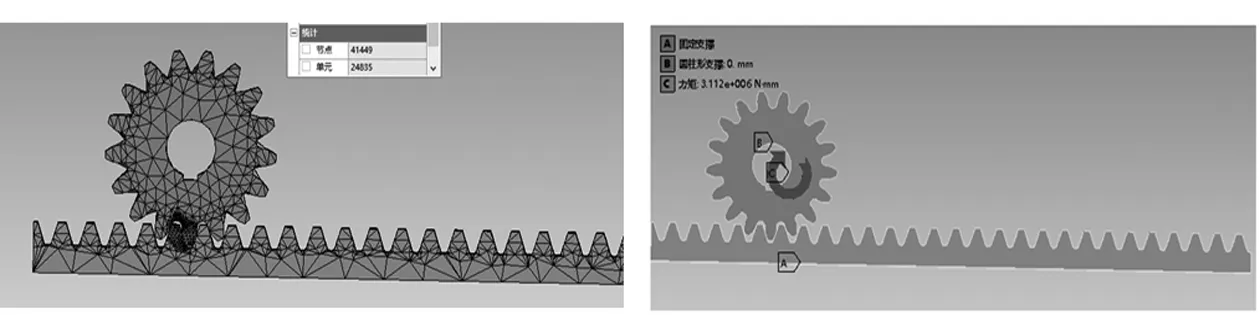
图2 网格划分模型 图3 工况1求解模型

齿轮齿条传动机构在工况1条件下产生的齿根弯曲应力最大值为53.509 MPa，如图4所示，图5为工况1对应的齿面接触应力云图。

图4 工况1弯曲应力云图 图5 工况1接触应力云图

从工况1到工况6，齿轮的切向力Ft在不断增加，相应地，齿轮的齿根弯曲应力和齿面接触应力也在不断增加。根据表2中工况参数改变输入力矩，在6组工况条件下，通过静力学分析所得到的齿轮的弯曲应力和接触应力如表5所列。将有限元分析所得数据和理论计算结果进行对比，整理之后得到表6和表7结果。

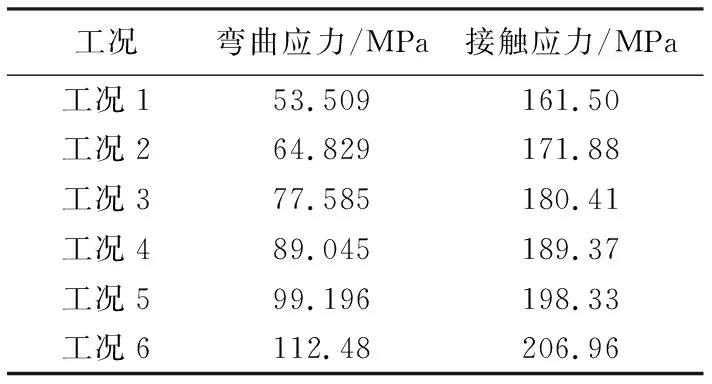
表5 弯曲应力与接触应力有限元分析结果

表6 齿轮弯曲应力对比

表7 齿轮接触应力对比

不管是齿轮弯曲应力还是齿面接触应力，理论计算结果和静力学分析结果相差在10%左右，考虑到误差因素的影响，可以把它们近似看作相等，两种方法互为证明，验证了采用这两种方法来计算齿轮弯曲强度和接触强度的可行性和准确性。

4 结 论

文中针对齿轮齿条起升机构，参考实际情况，模拟设置了6组不同的工况，对齿轮的弯曲强度和接触强度展开了理论计算和有限元分析，并将得到的结果进行了对比，得到了以下结论。

(1) 选择“ISO齿轮弯曲应力公式”和“Hertz接触理论”对齿轮弯曲应力和接触应力进行了分析计算，发现6组工况条件下算得的齿轮的弯曲、接触应力随切向力的增大而增大。

(2) 建立了齿轮齿条传动机构的装配模型，进行了静力学分析，通过有限元分析求解了6组工况下的齿轮弯曲应力及接触应力并将结果与理论计算进行对比。分析发现齿轮弯曲应力最大值出现在齿根位置，接触应力主要分布在轮齿表面，并且理论计算与有限元分析得出的数据差值在10%左右，验证了理论计算法和有限元分析法求解齿轮弯曲强度和接触强度的可行性和准确性。