MMC拓扑优化方法的拉-压杆模型研究

陈 阵，李元松，杨毛毛，陶文华，占森方

(武汉工程大学 土木工程与建筑学院，湖北 武汉 430073)

0 前 言

拉-压杆模型是由桁架模型发展来的一种针对混凝土构件中应力扰动区设计的一种类桁架模型的配筋计算方法。它的主要原理是通过由拉杆、压杆和节点三部分组成的理想桁架来近似模拟混凝土结构中力的传递路径，进而对结构进行配筋设计[1]。从最初的Monier采用箍筋加固结构，从平面桁架模型到软化桁架模型，拉-压杆模型配筋方法不断地发展完善，逐渐成为了一种被广泛接受使用的混凝土结构设计方法[2-3]，现已被多个国家纳入规范体系中。常见的拉-压杆模型构建方法有传统经验法、应力迹线法、荷载路径法、拓扑优化法等[4-5]。拉-压杆模型由于只需满足平衡条件和屈服准则，不需考虑固体力学中的应变协调，因此对于一个给定的问题，拉-压杆模型的构形并不唯一，这也是传统经验法与应力迹线法等方法建立的拉-压杆模型的正确性常常受限于设计人员的直觉和经验的原因。

拓扑优化法的应用使得这一现状发生了转变，设计人员可以通过拓扑优化结果构建拉-压杆模型，这大大减少了传统经验方法中人为因素的干扰[6]。常见的优化方法包括变密度法、水平集法等方法[7-8]。此类拓扑优化方法为隐式求解法，求解结果都是基于像素或是基于节点的，因此结果边界模糊，具有棋盘格现象，在此基础上构建拉-压杆模型也不够准确，大连理工大学郭旭教授及其团队通过多年的研究提出了一种基于可移动变形组件(moving morphable components，简称MMC)的拓扑优化方法。作为一种显式的拓扑优化方法，该方法的基本思想是将组件作为表达结构拓扑的基本单元，通过组件的移动、变形、交叉和重叠来模拟结构拓扑的变化，从而得到最优的拓扑[9-11]。由于MMC法拓扑优化是基于组件而不是单元，因此设计变量更少求解效率更高，另一方面组件是通过显示拓扑函数描述，优化后的结果边界清晰，不存在灰度单元，可以直接由拓扑优化结果构建拉-压杆模型，减少了设计者的参与和修改。乔文正等[12-13]对基MMC法构建拉-压杆模型做出了系列的研究，对牛腿、开洞深梁等构建了相应的模型。

本文对MMC拓扑优化法的原理与优化步骤等进行归纳介绍，并以某一深梁为研究对象，基于可移动变形组件框架，利用有限元分析和灵敏度分析求解设计域的结构场，更新设计变量，通过求解体积约束下柔度最小的优化问题，得到最佳拓扑优化结果并构建深梁的拉-压杆模型并通过Abaqus软件优化进行对比。以某一深梁的实例验证了基于MMC拓扑优化法构建拉-压杆模型的可行性与简便性。

1 MMC法优化原理

1.1 优化原理

以往的拓扑优化方法例如水平集法、SIMP法等，其原理都是通过材料将整个结构填充，然后通过不断迭代去除非必要的部分来实现结构的拓扑优化，由于它们自身的优化特性，优化结果往往是基于像素或是水平集函数隐式描述的。MMC法基本思想是用一些可以移动、变形的组件作为结构拓扑的基本单元，在MMC框架下，组件可以自由地移动、覆盖、融合和消失，因此可以通过改变其几何特征参数，和施加在结构上相应的工况进行优化，得到结构的最佳拓扑结果，其结果边界清晰明了，有助于设计人员进一步设计工作。

1.2 结构拓扑函数描述

每个组件的描述方程都是显示的，可以由变量x，y通过一定函数关系表达[12]，此处给出结构拓扑函数，采用二次变厚度组件作为结构基本单元，如图1所示。

图1 组件结构示意图

(1)

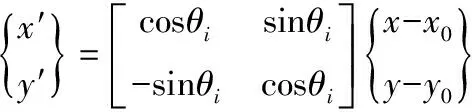
(2)

(3)

式中，L为组件在x′方向上的半长；(x0,y0)表示第i个组件中心点的坐标;θi表示第i个组件沿逆时针方向的角度；p是一个比较大的偶数，一般取p= 6，t1i,t2i,t3i表示第i个组件二次变化的3个宽度；组件的设计变量可以表示为di=(xoi,yoi,Li,t1i,t2i,t3i,θi)。

2 MMC法拓扑优化设计流程

在确定结构大小、边界条件以及荷载状况下，以结构柔度最小为目标，结构体积为约束，通过MMC拓扑优化法建立优化模型，以有限元和灵敏度进行准确的数值分析，采用可移动渐进线算法(MMA算法)更新设计变量，求解拓扑优化数学模型的算法流程如图2所示。

图2 MMC拓扑优化程序设计流程图

3 数值算例

深梁作为典型的不符合平截面假定的一类钢筋混凝土构件，选择一深梁作为实例进行优化。本文的研究是在张维声[11]研究基础上进行的，假设结构处于平面应力状态，几何、材料及荷载等参数均采用无量纲形式，厚度取单位1，材料弹性模量E为1，泊松比v为0.3，加载大小均为单位荷载。构建的拉-压杆模型中，拉杆为实线、压杆为虚线。

深梁梁高取1.0 m，宽取1.0 m，梁上作用荷载F为100 kN，网格划分为50×50，材料体积分数约束上限为0.4，深梁结构及对应荷载情况下的拉-压杆模型如图3所示。基于MMC拓扑优化与Abaqus拓扑优化进行对比。

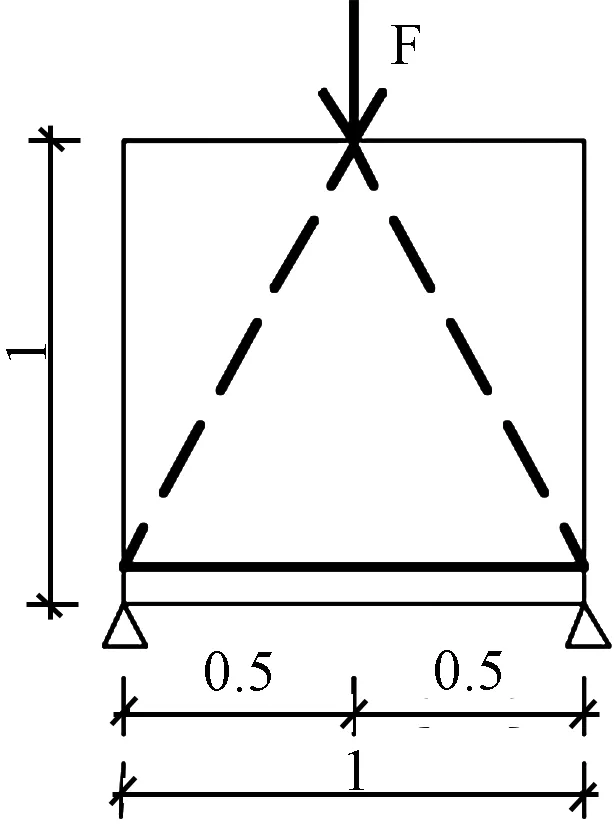
(a)单荷载深梁

3.1 单荷载下深梁

图4为单荷载下深梁优化网格与结果，在MMC的优化过程中，初始布局选择8个组件，设计变量个数为56个。伴随着迭代次数的增加，这些组件通过移动、膨胀、收缩、相交和重叠来实现结构拓扑的变化，最终达到收敛要求。从图中的优化过程可以发现MMC优化过程清晰明了、边界光滑、求解效率快，没有Abaqus优化方法结果导致的模糊粗糙边界。优化结果为深梁中部所受荷载通过两个压杆传递到支座处，支座上方形成一根拉杆将两根压杆连接。

(a)MMC初始布局图

(c)MMC拓扑优化结果

3.2 多荷载下深梁

图5为受多荷载的深梁优化过程。同理，在多荷载作用下深梁的MMC的优化过程中，初始设计为32个组件，设计变量数为224个，通过设计变量不断更新，最终达到目标收敛要求，收敛结果见图5(a)。MMC拓扑优化结果清晰，设计者可以清晰明了，设计者可从拓扑优化结果中建立起结构相应的拉-压杆模型。荷载向下通过压杆传递到支座处，中间与下部区域存在拉杆保证横向平衡。

而在Abaqus拓扑优化结果中，图4(d)与图5(b)可以清晰看到在靠近深梁底部处，无论是单荷载或是多荷载下，在深梁下部都缺少相应的底部拉杆，造成这种结果的原因是多种的，此处不进行讨论。而基于MMC拓扑优化法却没有这种现象，可以直接通过结果构建拉-压杆模型，这十分方便设计者去构建结构的拉-压杆模型。但在MMC法中，组件的数量、大小及设置的循环次数等都会对结果产生较大影响，其中组件数量的影响最为关键，使用MMC法时要选择合适的组件数量。

(a)MMC优化结果

4 结 论

本文介绍了MMC法的优化原理以及优化步骤，通过将MMC拓扑优化法应用于深梁这一典型不符合平截面假定的构件，研究了基于单荷载和多个荷载情况下深梁拉-压杆模型的构建，并将基于MMC法与Abaqus优化建立拉-压杆模型进行对比得出以下的结论。

1)基于MMC拓扑优化方法应用于拉-压杆模型构建是可行的。

2)MMC法作为显式的拓扑优化方法，克服了隐式求解方法存在的中间密度单元，边界锯齿化等问题，拉-压杆模型边界光滑。

3)基于MMC法构建拉-压杆模型去除了单元格的影响，优化结果可直接作为结构相应拉-压杆模型，但使用时要注意组件的合理配置，而基于Abaqus所建立的拉-压杆模型需要设计者更多的完善，基于MMC法构建拉-压杆模型更加方便设计者工作。

[ID:013410]