基于熵权综合评价法的动力电池壳首道次拉深成形参数优化

任振宝 曹春平

南京理工大学机械工程学院，南京，210094

0 引言

动力电池壳是一种高矩形的薄壁盒形件，须经多道次拉深成形。拉深时，圆角部位相当于圆筒件拉深，直边部位相当于弯曲变形，这两个部位的变形相互影响。高矩形动力电池壳成形特点是受力分布不均匀、变形分布不均匀、材料流动不均匀，因此拉深成形中容易出现起皱、破裂等缺陷，其中，首道次拉深变形最大，更容易发生起皱、破裂。传统方法通过反复试模和实验来生产电池壳，这种方法成本高、效率低，现在借助数值模拟仿真技术可以研究各工艺参数对成形的影响，提前预测板料在成形过程中的缺陷，通过优化工艺设计和工艺参数的方法避免起皱、破裂等缺陷，以减少试模、降低开发成本[1]。

国内外的学者对矩形盒冲压进行了研究。金飞翔等[2]对两种厚度的铝合金板材进行冲压仿真，分析了不同塑性变形硬化模型的结果，发现铝合金板材选用Hollomom方程进行仿真的效果更好。张红升等[3]研究了盒形件电控永磁技术的径向分区压边方法，通过控制压边力有效减少了产品的起皱。谢延敏等[4]利用数值模拟和灰色系统理论对方盒件进行参数优化，对获得的目标序列灰色关联度进行方差分析，获得了最优工艺参数，提高了方盒件质量，最终的产品无开裂和起皱。郭鹏等[5]建立了板料拉深过程中的压边力控制模型，将有限元仿真和深度强化学习进行集成，提高了盒形件成形质量。MANABE等[6]采用具有大应变速率依赖性的超塑性材料进行拉深试验，研究了压边力和冲头速度对法兰起皱行为和壁厚分布的影响，发现压边力对壁厚均匀分布有很大影响。YAGHOUBI等[7]研究了模具几何参数对铝合金深冲工艺的影响，以板料厚度最大减薄量和厚度均匀性为目标，采用神经网络和蜜蜂算法获得了优化的几何参数。LIU等[8]使用有限元分析模拟了矩形杯子的冲压过程，通过优化毛坯形状改善了产品的质量、降低了成本。DEMIRCI等[9]利用LS-DYNA 软件分析铝合金板料方盒件拉深成形问题，找到了方盒件不出现起皱和破裂的压边力范围。NACEUR等[10]结合逆向有限元法与梯度优化算法对盒形件毛坯形状进行优化。上述文献主要考虑破裂和起皱对制件成形质量的影响，较少考虑零件的厚度均匀性和模具接触力，并且缺乏多工艺参数之间交互作用对拉深成形影响的研究。

高矩形动力电池壳首道次拉深的变形量最大，容易出现破裂等问题，且后续拉深是在其基础上进行的，首道次拉深成形的质量将会影响最终产品的质量。因此本文以高矩形盒形件首道次拉深成形工艺为对象，综合考虑零件厚度均匀性及模具接触力，首先设计五因素四水平的正交试验表，研究各工艺参数对首道次拉深成形质量的影响，并在此基础上，采用基于熵权的综合评价法对影响电池壳首道次拉深成形性能的工艺参数进行优化分析，最后通过首道次拉深成形实验来验证工艺优化结果的可行性。

1 工艺分析及有限元模型的建立

1.1 拉深成形工艺分析

本文的动力电池壳是高矩形，该零件的底部圆角半径r=3 mm，长度A=173.6 mm，宽度B=53.5 mm，高度H=199.7 mm，底部厚度t=1.5 mm，侧壁厚度为0.6 mm。成形后的零件不能有起皱和破裂，表面没有划痕和拉伤。该电池壳属于典型的高矩形壳，需经过多道次普通拉深和变薄拉深，其中首道次拉深是本文的主要研究内容。

该零件采用的材料为轧制铝合金板材AL3003H14，毛坯厚度为1.5 mm。材料性能参数为：密度2.7×103kg/m3，弹性模量69 GPa，泊松比0.33，屈服强度125 MPa，抗拉强度150 MPa。

1.2 工序设计

零件的相对高度H/B较大，圆角部分对直边部分的影响较大，所以直边部分的变形小于圆角部分的变形，材料流动不均匀。因此，设计拉深工序图时，应使变形区各处的伸长尽量均匀，毛坯长与宽的比例应适当。

选用厚度为1.5 mm的毛坯，由变薄拉深的方法计算毛坯直径，即通过体积不变原则初步计算毛坯直径：

式中，V1为电池壳底部体积；V2为电池壳侧面体积；tr为动力电池壳毛坯的厚度。

由V1=13 931.4 mm3，V2=54 422.3 mm3，tr=1.5 mm得D=241 mm。在计算得出的毛坯直径基础上进行优化调整，最终确定电池壳毛坯为长309.6 mm、宽243.6 mm的椭圆。

根据《冲压模具简明设计手册》推荐的高矩形盒冲压工艺方法设计电池壳多道次拉深工序，共需4道椭圆件普通拉深和2道矩形盒变薄拉深，其中，首道次拉深的凹模截面为长240.1 mm、宽145.96 mm的椭圆。

1.3 有限元模型的建立

电池壳首道次拉深工艺模型包括凹模、凸模、毛坯、压边圈。将SolidWorks建立的几何模型转为IGS格式，再导入DYNAFORM软件。毛坯和模具均是对称结构，为提高计算效率，将有限元模型简化为1/4进行仿真，首道次拉深的有限元模型如图1所示。

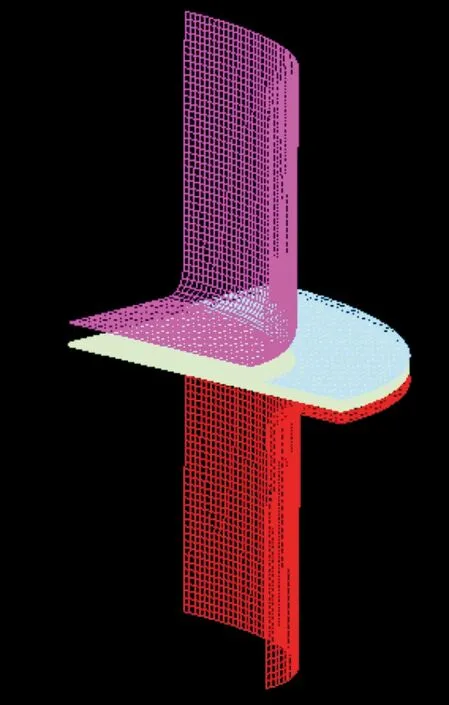
图1 首道次拉深有限元模型Fig.1 Finite element model of the first pass deep drawing

电池壳后续的拉深成形中，厚度会明显减小，导致壳单元厚度方向的力学行为表征不准确，无法有效反映变薄拉深过程中的材料减薄现象[11]，得出的结果精确度不高。针对这种情况，本文的毛坯采用六面体单元建模，以提高仿真结果的精确度。毛坯的厚度为1.5 mm，在厚度方向上设置3层网格。凸模、凹模、压边圈均作为刚体处理并采用BT壳单元建模，壳单元形状为四边形，单元尺寸为3 mm×3 mm。有限元模型中，凹模截面形状为长120.05 mm、宽72.98 mm的椭圆形，首道次拉深成形的高度为80 mm，虚拟拉深速度为2 m/s。设置参数后提交LS-DYNA求解器求解，运用eta/POST进行后处理[12]。

2 正交试验设计及结果分析

2.1 正交试验方案

电池壳首道次拉深成形的椭圆件质量受多个工艺参数共同影响，因此，需要研究多个参数对拉深成形质量的交互作用，进而优化参数。以首道次拉深成形椭圆件的最大减薄率Y1(表征制件的破裂趋势)、最大增厚率Y2(表征制件的起皱趋势)、最大凸模接触力Y3、最大厚度差Y4为评价指标。工程应用中，减薄率不应超过30%，增厚率不能超过25%，因此在最大减薄率30%、最大增厚率25%条件下，Y1、Y2均越小越好[13]，因此在满足要求下，Y1、Y2越小越好。Y3反映的是模具的接触力，其值越小，对模具的损害越小；Y4反映制件的厚度均匀性，其值越小，产品厚度越均匀。

影响电池壳首道次拉深成形的因素有压边力、凹模圆角半径、凸模圆角半径、模具间隙、摩擦因数、毛坯尺寸等，其中，毛坯尺寸对成形的影响较小，毛坯尺寸取大会浪费材料，取小可能导致修边余量不足、影响精度，因此本文通过零件形状反求毛坯尺寸。在确定毛坯形状及尺寸后，选取压边力、凹模圆角半径、凸模圆角半径、模具间隙、摩擦因数为试验因素，每个因素选取4个水平，如表1所示。采用L16(45)阵列田口正交试验表[14]，正交试验方案及结果如表2所示。

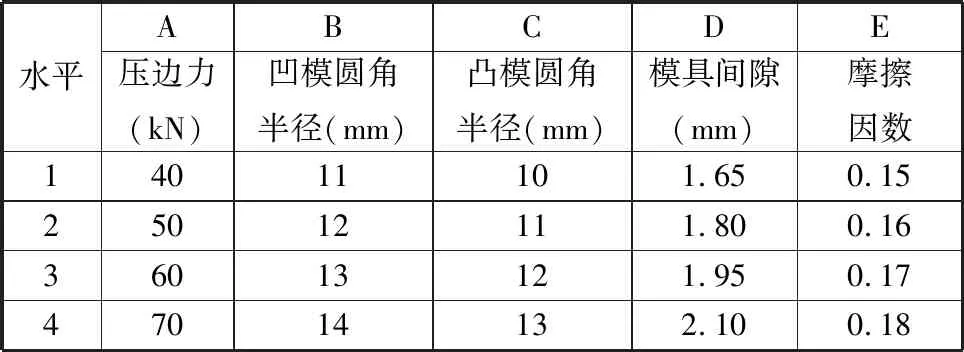
表1 正交试验因素及水平

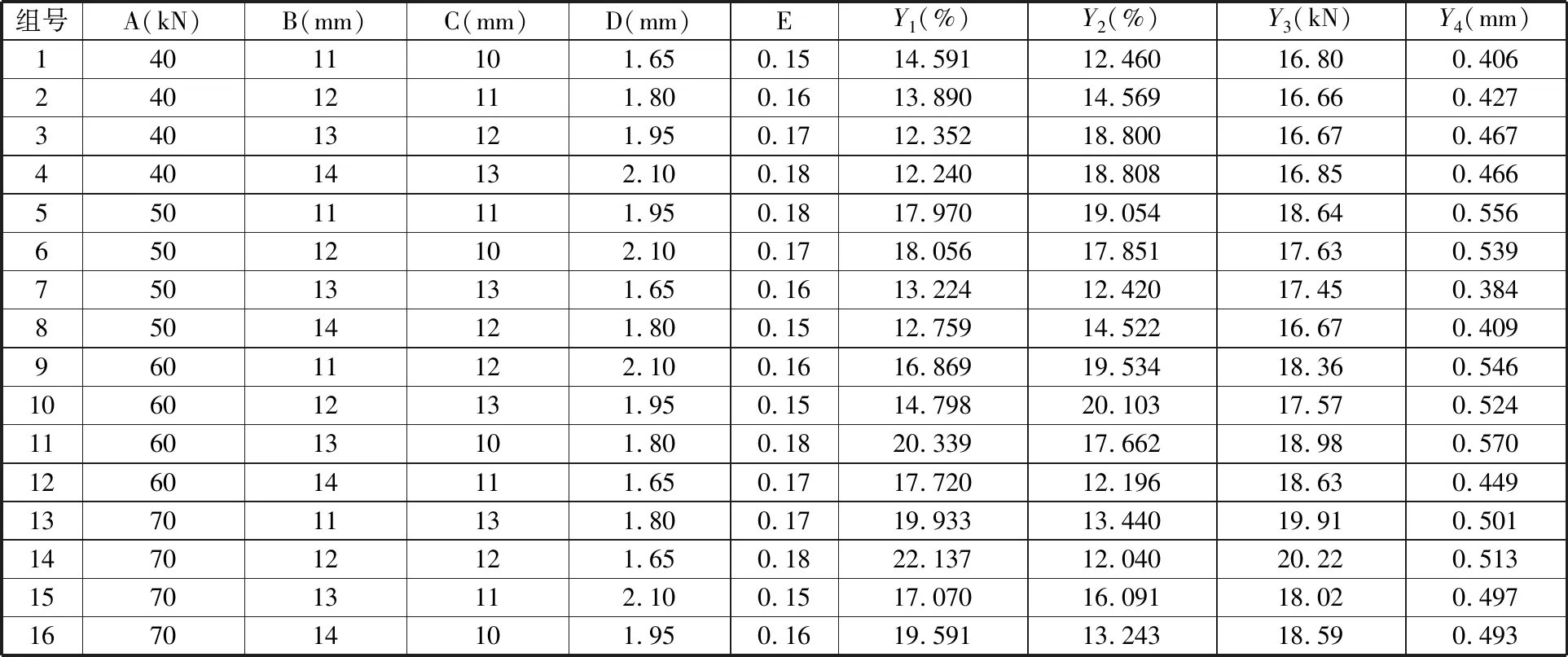
表2 正交试验方案及结果

2.2 正交试验结果分析

对表2所示的正交试验结果进行极差分析，可得到各工艺参数对4个评价指标的影响程度[15]，计算得到各评价指标的分析结果，如表3所示，其中，Ri(i=1，2，3，4)为因素i的极差。极差越小，该因素对评价指标的影响越小；极差越大，该因素对评价指标的影响越大。通过表3可以得到工艺参数对各评价指标的影响排序。

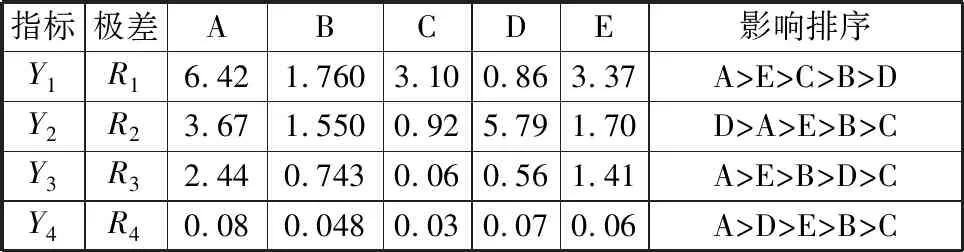
表3 极差分析结果

为得出各评价指标随参数水平变化的规律，对正交试验数据进行主效应(描述各工艺参数对各评价指标影响大小的度量)分析。采用Minitab获得各评价指标主效应图(图2)。

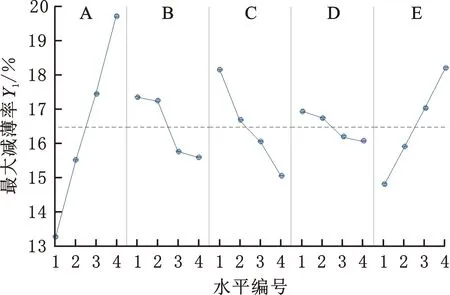
(a)最大减薄率均值的主效应图

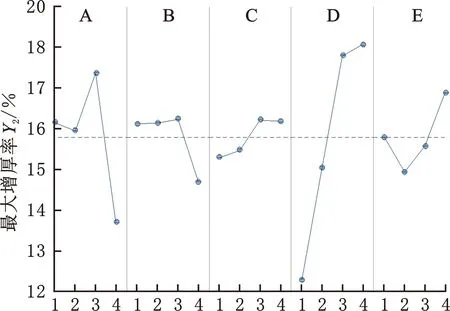
(b)最大增厚率均值的主效应图

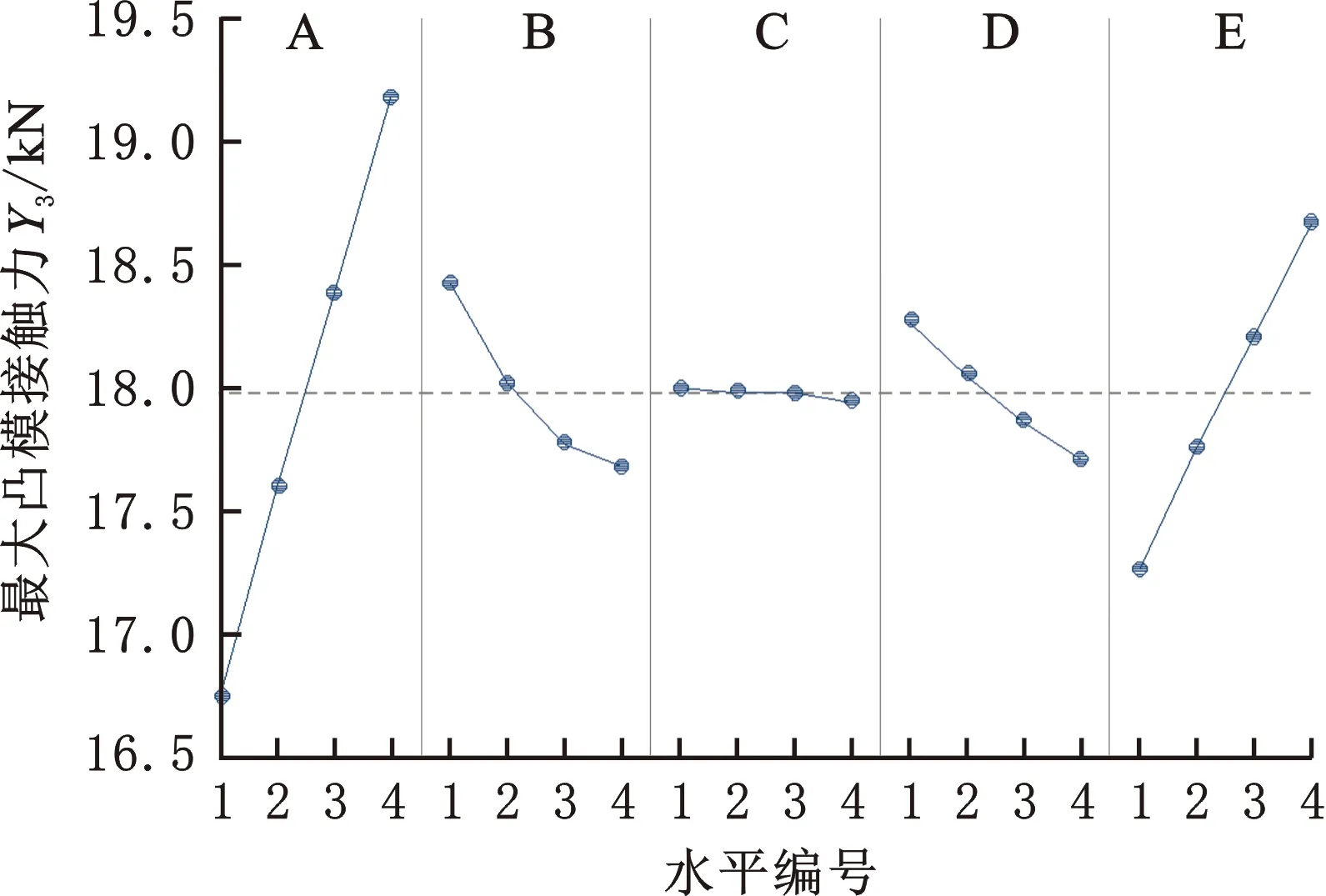
(c)最大凸模接触力均值的主效应图

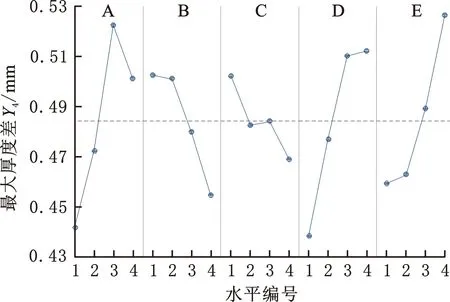
(d) 最大厚度差均值的主效应图图2 评价指标随各因素水平变化的趋势Fig.2 The trend of evaluation indicators with the level of various factors

由图2a可知，最大减薄率随压边力和摩擦因数的增大而增大，随凹模圆角半径、凸模圆角半径和模具间隙的增大而减小。由图2b可知，模具间隙的回归线最陡，对最大增厚率影响最大，随着模具间隙的增大，最大增厚率增大。由图2c可知，压边力、摩擦因数均和最大凸模接触力正相关；凹模圆角半径、模具间隙和最大凸模接触力负相关；凸模圆角半径的曲线几乎为水平线，主效应影响不显著。由图2d可知，随着模具间隙、摩擦因数的增大，最大厚度差增长；随着压边力的增大，最大厚度差先增后减；凹模圆角半径、凸模圆角半径和最大厚度差负相关。

3 多目标工艺参数优化

3.1 基于熵权法的综合评价

由上述分析可知，各工艺参数对4个评价指标的影响程度不同，各成形质量目标相互关联，很难对制件进行定量评价[16]，故需要综合分析各工艺参数对这4个评价指标的影响，将多指标的问题按一定规则转化为单指标问题，实现对工艺参数的优选。本文提出一种基于熵权的综合评价法进行工艺参数优化，先计算各个评价指标的熵值，得到每个评价指标的权重系数，然后通过加权线性方法计算出综合评分，由分数高低选出最优参数组合。

熵值法是一种客观赋权法，根据目标在结果中的重要性赋予相应的权重系数[17]。计算过程中，某个评价指标的熵值越小，该评价指标的样本值差异越大，提供的信息量越大，对应权重系数应越大[18]。应用熵值法计算权重系数，首先需要对原始正交试验数据进行归一化。正交试验时，最大减薄率、最大增厚率、最大模具接触力、最大厚度差为首道次拉深成形质量的评价指标，这4个指标均越小越好，因此需要采用负向指标进行归一化处理：

式中，Yij、rij分别为归一化处理前后的数据，下标表示第i组方案的第j个评价指标；maxYij、minYij分别为归一化处理前第i组方案的第j个评价指标的最大值和最小值。

然后对归一化后的评价指标矩阵计算熵值，第j个评价指标的熵值为

最后根据评价指标的熵值计算出相应的权重系数：

得到不同评价指标的权重系数后，通过加权线性方法计算出综合评分：

将计算得出的16组试验的综合评分结果填入表4。由表4得出，第7组试验A2B3C4D1E2的综合评分91.3最高，该组的工艺参数为：压边力50 kN、凹模圆角半径13 mm、凸模圆角半径13 mm、模具间隙1.65 mm、摩擦因数0.16。

通过熵权综合评价法将4个评价指标转化为单指标——综合分Z，Z越大说明拉深成形的质量越好。对表4中的数据进行极差分析，可得到各参数对综合分的影响，如表5所示。

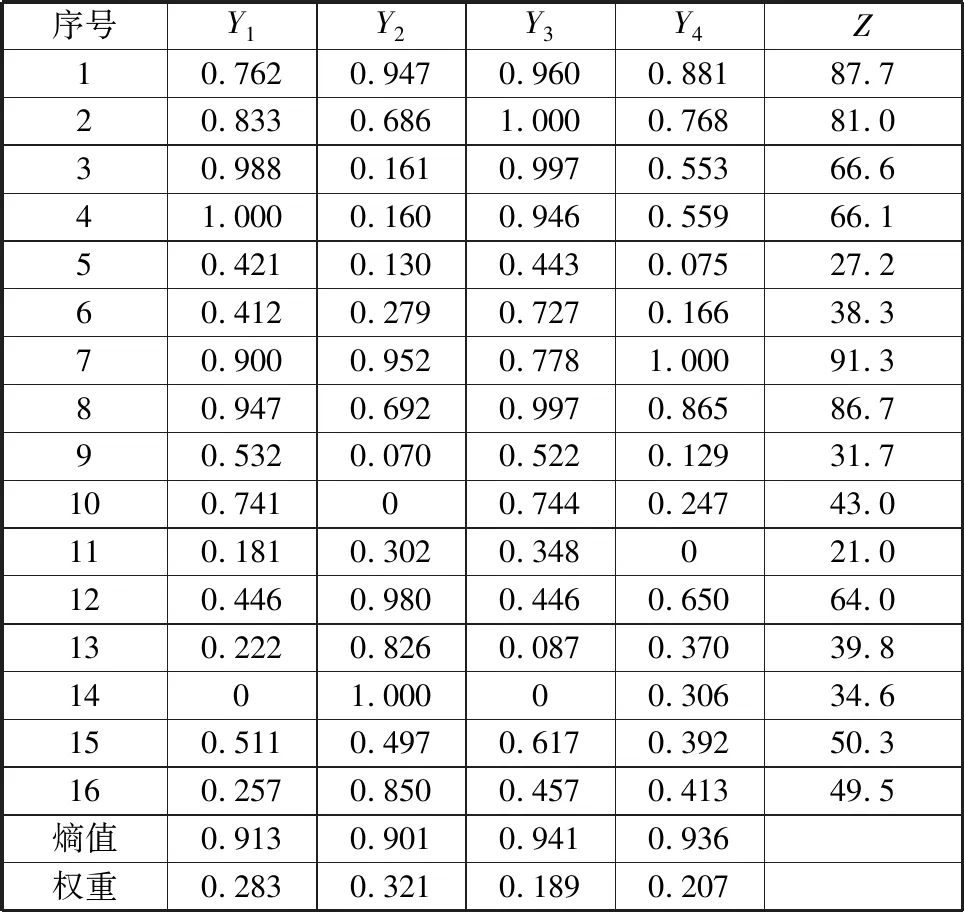
表4 数据标准化及计算结果

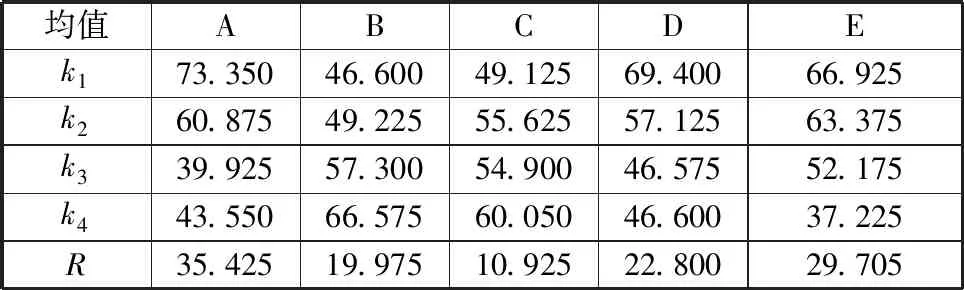
表5 综合分的极差分析

由表5可知，压边力对综合分的影响最大，凸模圆角半径的影响最小，各工艺参数对综合评价指标的影响顺序为A>E>D>B>C。参数均值最大的水平组成的参数组合为A1B4C4D1E1。将组合A1B4C4D1E1与正交试验中最高分的参数组合A2B3C4D1E2进行比较，从而确定制件的综合质量最高的方案，得到的结果如表6所示。

表6 优选方案结果

由表6知，参数组合A1B4C4D1E1的得分最高，该组合除最大增厚率略大于参数组合A2B3C4D1E2之外，最大减薄率、最大凸模接触力和最大厚度差均小于参数组合A2B3C4D1E2。因此，确定电池壳首道次拉深成形最优的工艺参数组合为A1B4C4D1E1，即压边力40 kN、凹模圆角半径14 mm、凸模圆角半径13 mm、模具间隙1.65 mm、摩擦因数0.15。

3.2 仿真优化结果

选用最优的工艺参数组合进行仿真，得到的制件减薄仿真结果如图3a所示，图中的色标代表仿真得到的减薄率，对比图3b可知，优化后的制件减薄率和增厚率均明显减小。由图4可知，优化后的凸模接触力减小。

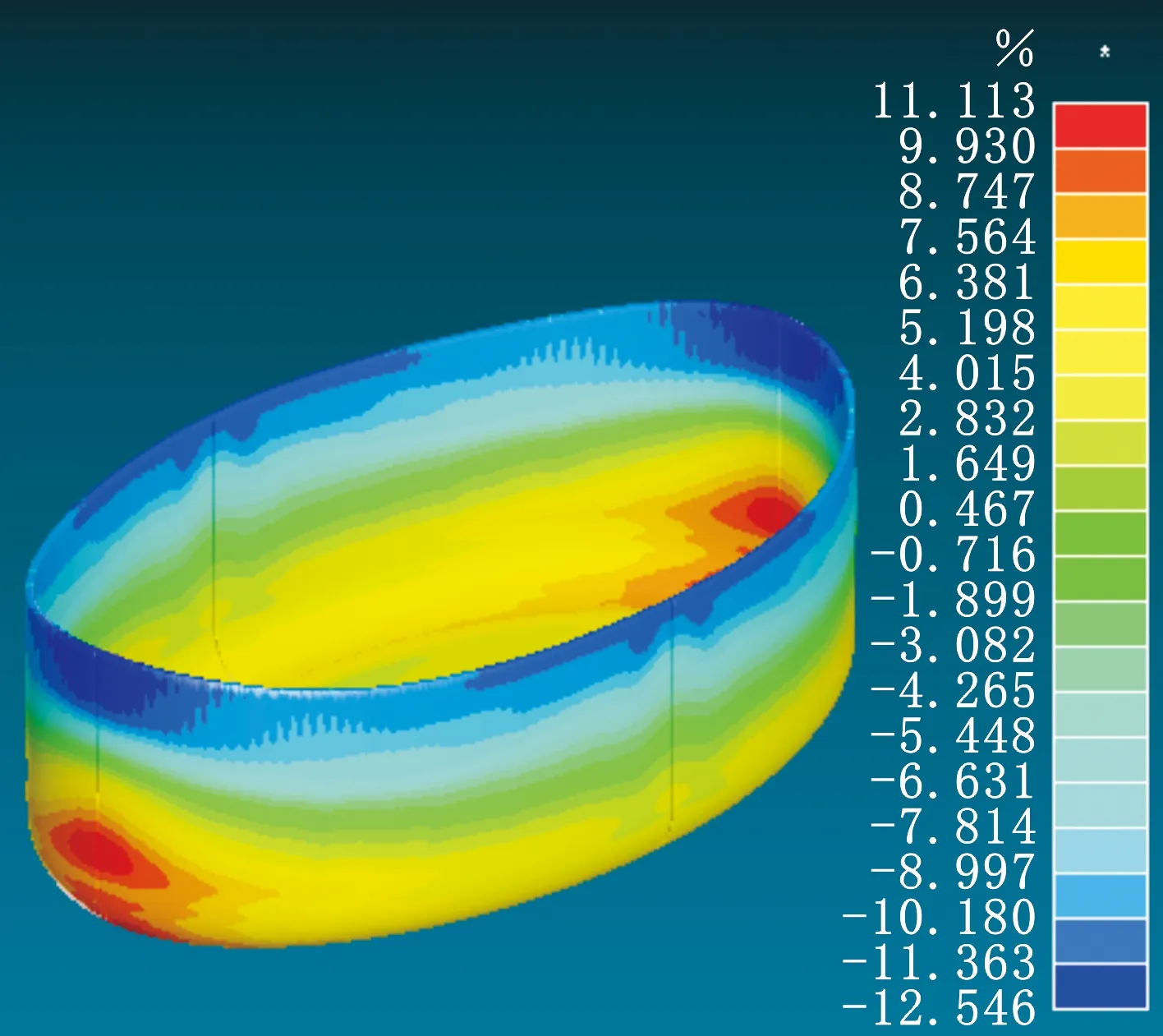
(a)优化后

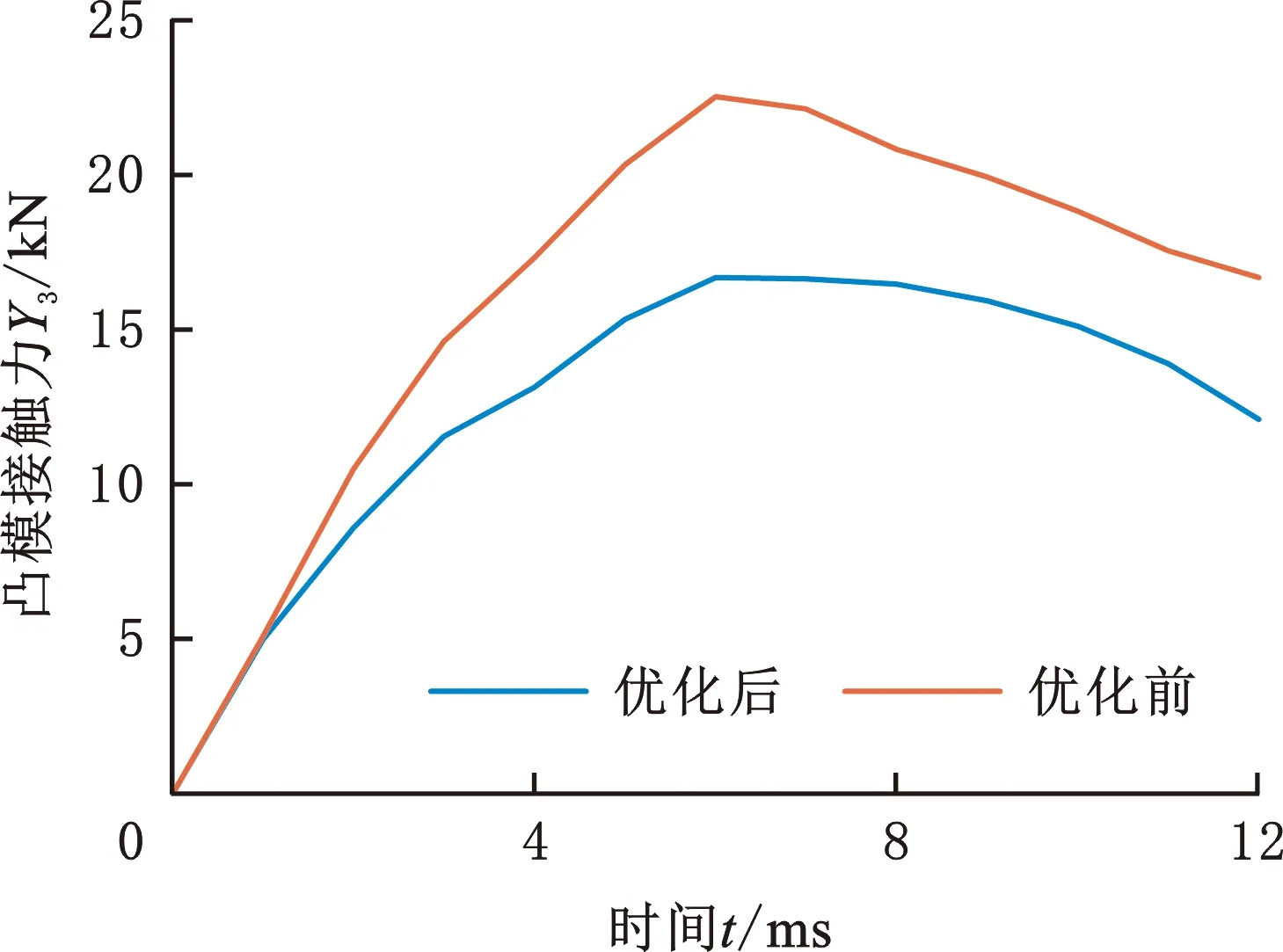
图4 优化前后的首道次拉深凸模接触力Fig.4 Contact force of the first drawing punch before and after optimization

优化前后的仿真数据如表7所示。优化后的各评价指标均减小，制件的最大减薄率Y1减小50.9%，最大增厚率Y2减小41.2%，最大凸模接触力Y3减小25.3%，最大厚度差Y4减小46.1%。制件无破裂、起皱缺陷，壁厚更加均匀，模具接触力减小。

表7 优化前后的仿真结果

3.3 实验验证

为验证最优工艺参数的可行性，采用最优工艺参数进行电池壳首道次拉深成形。本文试验中的摩擦因数通过试验测得，将毛坯与模具钢板放于水平试验平台上，进行拉力测试。实验中使用黏度小的润滑油，测得其摩擦因数为0.15，在该摩擦因数下，采用剩余的最优参数进行试验。试验设备如图5所示。图6所示为采用最优工艺参数组合得到的椭圆件，零件无破裂、起皱等缺陷。

图5 试模设备Fig.5 Test mold equipment

图6 首道次拉深成形件Fig.6 The first-pass deep-drawn part

本文采用尖角千分尺来测量首道次拉深成形件表面的厚度以及通过拉深成形试验机来获得拉深过程中的最大凸模接触力。试验获得的数据以及仿真的数据对比如表8所示，由表可知，试验和仿真的结果基本一致表明了数值模拟和熵权综合评价可以用于拉深工艺参数优化中。

表8 仿真结果与实验结果

4 结论

(1)运用正交试验设计与拉深数值模拟相结合的方法，研究了压边力、凹模圆角半径、凸模圆角半径、模具间隙、摩擦因数对制件成形的影响。由极差分析法可得工艺参数对各评价指标的影响顺序，通过主效应图可得各评价指标随参数水平变化的规律。

(2)提出一种基于熵权的综合评价法优化多目标工艺参数，最大减薄率、最大增厚率、最大凸模接触力、最大厚度差的权重系数分别为0.283、0.321、0.189、0.207。方案A2B3C4D1E2是正交试验中最高分数，该方案的工艺参数组合为：压边力50 kN、凹模圆角半径13 mm、凸模圆角半径13 mm、模具间隙1.65 mm、摩擦因数0.16。

(3)采用极差分析得出各工艺参数对综合评价指标的影响顺序为：压边力>摩擦因数>模具间隙>凹模圆角半径>凸模圆角半径，得出的优选工艺参数组合为A1B4C4D1E1，该方案对应的工艺参数为：压边力40 kN、凹模圆角半径14 mm、凸模圆角半径13 mm、模具间隙1.65 mm、摩擦因数0.15，方案对应的综合分数为95.5，优于方案A2B3C4D1E2。因此，确定电池壳首道次拉深成形最优工艺参数组合为A1B4C4D1E1，优化后制件的各评价指标均显著减小，成形质量远优于优化前。

(4)实际试模结果和仿真结果基本一致，验证了数值模拟和多参数优化的可行性。